Received 27 January 2015; accepted 16 February 2015; published 25 February 2015

ABSTRACT

In this paper, we propose a new time dependent model for solving total variation (TV) minimi- zation problem in image denoising. The main idea is to apply a priori smoothness on the solution image. This is a constrained optimization type of numerical algorithm for removing noise from images. The constraints are imposed using Lagrange’s multipliers and the solution is obtained using the gradient projection method. 1D and 2D numerical experimental results by explicit numerical schemes are discussed.

Keywords:

Total Variation, Image Denoising, Signal Denoising

1. Introduction

In many image processing problems, a denoising step is required to remove noise or spurious details from corrupted images. The presence of noise in images is unavoidable. It may be introduced at the stage of image formation like image recording, image transmission, etc. These random distortions make it difficult to perform any required image analysis. For example, the feature oriented enhancement introduced in [1] is very effective in restoring blurry images, but it can be “frozen” by an oscillatory noise component. Even a small amount of noise is harmful when high accuracy is required, especially in case of medical images.

In practice, to estimate a true signal in noise, the most frequently used methods are based on the least squares criteria. This procedure is L²-norm dependent. L²-norm based regularization is known to remove high frequency components in denoised images and make them appear smooth.

Most of the classical image deblurring or denoising techniques, due to linear and global approach, are contaminated by Gibb’s phenomenon resulting into smearing near edges. In order to preserve edges Rudin et al. [2] [3] introduced total variation (TV) norm models based on variational approach. TV norms are essentially L¹ norms derivatives, hence L¹ estimation procedures are more appropriate for the subject of image restoration. For more details we refer to [1] [4] -[7] .

In this paper we present a new time dependent model constructed by evolving the Euler-Lagrange equations of the optimization problem. We propose to apply priori smoothness on the solution image and then denoise it by minimizing the total variation norm of the estimated solution. We have tested our algorithm on various types of signals and images and found our model (11) better than previously known model (10). To quantify results, the experimental values in terms of PSNR are given in Tables 1-3.

2. Image Denoising Models

Formation of a noisy image is typically modeled as

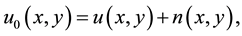(1)

where 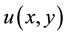denote the desired clean image, 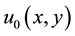denote the pixel values of a noisy image for, 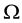is a bounded open subset of 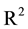and is additive white noise assumed to be close to Gaussian. The values 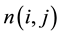of n at the pixels 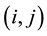are independent random variables, each with a Gaussian distribution of zero mean and variance.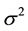

We wish to reconstruct u from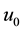. Most conventional variational methods involve a least squares fit because this leads to linear equations. The first attempt along these lines was made by Phillips [8] and later refined by Twomey et al. [9] [10] in one-dimensional case. In two dimensional continuous framework their constrained minimization problem is,

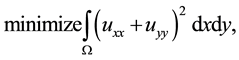(2)

subject to constraints involving the mean

(3)

and standard deviation

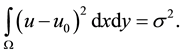(4)

The resulting linear system is now easy to solve using modern numerical techniques.

The total variation based image denoising model, which is based on the constrained minimization problem appeared in [2] , is as follows:

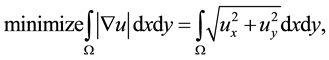(5)

subject to constraints

(6)

and

(7)

The first constraint corresponds to the assumption that the noise has zero mean, and the second constraint uses a priori information that the standard deviation of the noise is.

The Euler-Lagrange equation is given by,

(8)

in, with on the boundary of the domain.

Since (8) is not well defined at points where, due to the presence of the term, it is common to slightly perturb the TV algorithm to become

(9)

where is a small positive parameter [11] .

The solution procedure uses a parabolic equation with time as an evolution parameter, or equivalently, the gradient descent method. This means that we solve

(10)

for with given as initial data and on the boundary of the domain.

Applying a priori smoothness on the solution image, our new time dependent model becomes,

(11)

for with given as initial data and on the boundary of the domain. It should be noticed that (11) only replaces u in (10) by its estimate.

Witkin [12] noticed that the convolution of the signal with Gaussians at each scale was equivalent to solving the heat equation with the signal as initial datum. The term, which appears inside the divergence term of (11), is simply the gradient of the solution at time of the heat equation with as initial datum. In order to preserve the notion of scale in the gradient estimate, it is convenient that this kernel depends on a scale parameter [13] . In fact, the function can be considered as “low-pass filter” or any smoothing kernel, i.e., a denoising technique is used before solving the nonlinear diffusion problem [14] [15] .

The first constraint (8) is dropped because it is automatically enforced by the evolution procedure, i.e., the mean of is the same as that of. As t increases, a denoised version of image is realised.

To compute, we multiply (10) by and integrate by parts over. If steady state has been reached, the left side of (10) vanishes. We then have,

(12)

This gives us a dynamic value, which appears to converge as. The theoretical justification for this approach comes from the fact that it is merely the gradient projection method of Rosen [16] .

We still write as u. Let be the approximation to the value, where

(13)

The modified initial data are chosen so that the constraints are satisfied initially, i.e., has mean zero and norm one.

The explicit partial derivatives of model (10) and model (11) can be expressed as:

(14)

We define the derivative terms as,

We let,

(15)

and

(16)

Then (14) reads as follows:

(17)

with boundary conditions

(18)

The explicit method is stable and convergent for, see [17] .

3. Time Dependent Model for 1D

The 2D model described before is more regular than the corresponding 1D model because the 1D original optimization problem is barely convex. For the sake of understanding the numerical behavior of our schemes, we also discuss the 1D model. The Euler-Lagrange equation in the 1D case reads as follows:

(19)

This equation can be written either as

(20)

using the small regularizing parameter introduced in [18] , or

(21)

using the -function.

Our model in 1D will be

(22)

where is small regularizing parameter. The parameter in this model is estimated from the local amount of noise. We have found for our model, through our numerical experiments in 1D, that can be estimated as the standard deviation of the noise.

We can also state our model in terms of the function as

(23)

In this paper, we approximate, see the reference [18] , by

(24)

These evolution models are initialized with the noisy signal, homogeneous Neumann boundary conditions, and with a prescribed Lagrange multiplier for slightly noisy signals.

We have estimated near the maximum value such that the explicit scheme is stable under appropriate

CFL restrictions [18] , provided is chosen to be the standard deviation of the noise.

The following is the explicit numerical scheme of model (22).

Let be the approximation to the value, where and. We define the derivative terms as,

We let,

(25)

Then (22) reads as follows:

(26)

4. Numerical Experiments for 1D

We, as an example, have taken 1D signals and

given in Figure 1(a) and Figure 1(b) respectively. When Gaussian white noise is added to them, we get noisy signals.

In our test, we will use the signal to noise ratio (SNR) of the signal u to measure the level of noise, defined as

(27)

where is the mean of the signal u, i.e., the ratio of the standard deviation of the signal over the standard deviation of the noise.

The standard deviation of noisy signals (given in Figure 1(c) and Figure 1(d)) are approximately and respectively whereas their SNR are 0.99 and 0.95 respectively.

We use (is the standard deviation of the noise) and the Langrange multiplier [18] . Figure 1(e) and Figure 1(f) represent the denoised signals after 80 iterations with and 1.12 respectively.

We have performed many other experiments on 1D signals obtaining similar results.

5. Numerical Experiments for 2D

In our tests, we use peak signal to noise ratio (PSNR) as a criteria for the quality of restoration. This quality is usually expressed in terms of the logarithmic decibel scale:

(28)

where are the differences of the pixel values between the original and denoised images and R is the maximum fluctuation in the input image data.

When Gaussian white noise with mean zero and variance is added to the original images, we get noisy images. In our experiment, we have considered the images corrupted with different levels of Gaussian noise. Figures 3(a)-(c), Figures 4(a)-(c) and Figures 5(a)-(c) contain noisy images with different levels of Gaussian noise. The results obtained by using models (10) and (11) are shown in Figures 3-5 and Tables 1-3. We have taken Lagrange multiplier as was used in references [19] and [11] . We can choose [11] , the smallest positive machine number.

We have used three gray scale images, Goldhill, Rice and Boat shown in Figure 2 for our denoising experiments.

The values of PSNR obtained using model (11) given in Tables 1-3 are larger than that of using model (10) at the same iteration number. Thus based on PSNR values and also on human perception, we conclude that the model (11) gives better denoised images than that of model (10).

6. Concluding Remarks

We have presented a new time dependent model (11) to solve the nonlinear total variation problem for image denoising. The main idea is to apply a priori smoothness on the solution image. Nonlinear explicit schemes are

used to discretize models (10) and (11). The model (11) gives larger PSNR values than that of model (10), at the same iteration numbers. Besides, a new time dependent model (22) to solve the signal denoising in 1D has also been given.

References