Journal of Signal and Information Processing
Vol.5 No.2(2014), Article ID:45990,10 pages DOI:10.4236/jsip.2014.52007
A Nonlinear Autoregressive Approach to Statistical Prediction of Disturbance Storm Time Geomagnetic Fluctuations Using Solar Data
Joseph M. Caswell
Neuroscience Research Group, Laurentian University, Sudbury, Canada
Email: jx_caswell@laurentian.ca
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 31 January 2014; revised 28 February 2014; accepted 18 March 2014
ABSTRACT
A nonlinear autoregressive approach with exogenous input is used as a novel method for statistical forecasting of the disturbance storm time index, a measure of space weather related to the ring current which surrounds the Earth, and fluctuations in disturbance storm time field strength as a result of incoming solar particles. This ring current produces a magnetic field which opposes the planetary geomagnetic field. Given the occurrence of solar activity hours or days before subsequent geomagnetic fluctuations and the potential effects that geomagnetic storms have on terrestrial systems, it would be useful to be able to predict geophysical parameters in advance using both historical disturbance storm time indices and external input of solar winds and the interplanetary magnetic field. By assessing various statistical techniques it is determined that artificial neural networks may be ideal for the prediction of disturbance storm time index values which may in turn be used to forecast geomagnetic storms. Furthermore, it is found that a Bayesian regularization neural network algorithm may be the most accurate model compared to both other forms of artificial neural network used and the linear models employing regression analyses.
Keywords:Space Weather, Geomagnetic Storms, Artificial Neural Networks, Solar Winds, NARX, Forecasting, Interplanetary Magnetic Field

1. Introduction
Many complex system interactions are present throughout the disciplines of geophysics and associated solar dynamics. A number of these processes remain outside the capability of standard statistical procedures, requiring equally complex computational models in order to more accurately reflect physical relationships. Artificial neural networks (ANN) form the basis for a number of computational models based on the mammalian brain. Instead of relying on linear correlative relationships among a particular dataset, ANNs are a form of machine learning in which the system learns to recognize an output variable based on an input variable series [1] . Data is processed through a number of interconnected “neurons” which form “synaptic connections” from the input nodes through a hidden layer before converging on the output neurons (e.g., Figure 1). Each input and hidden neuron consists of statistical weights which are capable of adaptation [2] , the exact parameters which are modified by an algorithm over the course of network training procedures. These weights essentially form the synaptic connections among neurons which activate during network construction. This form of computation is capable of operating in parallel units, much like the human nervous system. Because neural networks do not rely on linear correlations for learning, ANNs are capable of nonlinear modelling and may therefore provide a useful alternative approach to a number of both theoretical and real world problems. This includes geo and solar physics [3] , medical diagnosis [4] , pattern recognition [5] , and many other areas. The nonlinear approach used in ANN computations is particularly useful in the context of highly complex or “noisy” datasets.
Backpropagation algorithms constitute a primary basis for the construction of ANNs [6] . In general backpropagation, the delta rule is employed for updating the statistical weights of each neuron in the network using a gradient descent [7] . An activation function is applied to artificial neurons in both the input and hidden layers, which in this case was a sigmoid function (e.g., Equation (1) & Figure 2).
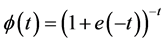 (1)
(1)

Figure 1. Feedforward artificial neural network diagram; input layer neurons, hidden layer neurons, output neuron (s), lines indicate data weights (“synaptic connections”). Image source: Glosser.ca.
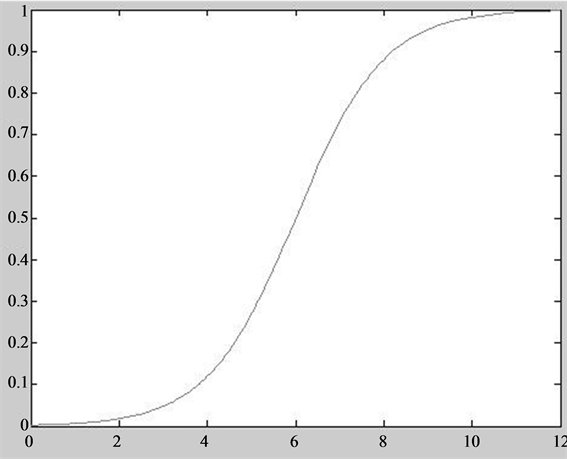
Figure 2. Plotted sigmoid function (logistic curve).
One of the primary training algorithms employed in ANN modelling is the Levenberg Marquardt Algorithm (LMANN). This particular method is a standard backpropagation curve fitting algorithm typically employed to solve generic problems using a damped least squares process [8] . While the LMANN option is a popular choice, it is capable of obtaining a local minimum only, and is therefore not always ideal for greater generalization [9] . However, a neural network trained using a Bayesian regularization algorithm (BRANN) has been shown to possess greater generalization than other ANNs and has demonstrated more robust results overall compared to standard backpropagation networks [10] . There are a number of other benefits associated with this particular learning algorithm summarized by Burden & Winkler [10] , including reduced probability of network “overtraining” or overfitting, reduced difficulty in cross validation, and more effective stopping procedures. Overfitting refers to a resultant model which describes random noise as opposed to the intended output, which will subsequently have poor overall predictive performance by overemphasizing minute data fluctuations. By integrating Bayesian probabilities, this also allows for greater accuracy in network learning, and probabilities associated with artificial neuron weights are updated according to newly observed data using a likelihood function (Equation (2)) which compares a standard Gaussian function with the updated observations.
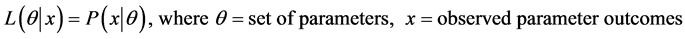 (2)
(2)
In the following analyses, two training algorithms were employed using a nonlinear autoregressive exogenous network (NARX). This particular form of ANN is used in time series modelling [11] in order to predict an outcome variable [y(t)] based on both d past values of the outcome variable and current and d past values of an external source of influence [x(t)], as illustrated in Equation (3). The fit of predicted output values can be compared to the original target values using simple correlation coefficients [12] , while an error term is also employed in order to further gauge predictive accuracy, typically presented as some forms of mean or summed squared error term (target-output).
 (3)
(3)
A number of novel approaches to space weather dynamics have been examined using ANN models. Many of these models possess useful real world applications which enable researchers to predict future values associated with various geo and solar physical systems. The NARX form of network used in this study was previously employed by Oliveira et al. [12] in order to simulate conditions of the interplanetary magnetic field (IMF) using ground observations associated with cosmic rays as the exogenous input. Furthermore, the disturbance storm time (DST) index, which was also the focus of this study, was recently examined using various measures of solar winds and the IMF [3] . The present study focuses on daily averages of simple, untransformed values obtained from a freely available online source (http://omniweb.gsfc.nasa.gov/).
The Earth’s magnetic field has an average static background intensity of ~50,000 nT [13] . Despite this relatively weak value, variations in geomagnetic activity have been shown to affect terrestrial systems including electronics and power systems [14] , and human health [15] , while even small perturbations of ~20 to 40 nT have been related to alterations in brain activity associated with altered states of consciousness [13] . One of many measures associated with geomagnetic activity, the DST index refers to the varying power of the ring current which surrounds the geosphere. The subsequent DST magnetic field opposes the geomagnetic field so that decreases in DST index accompany increases in geomagnetic activity. This specific measure is particularly useful in studying solar geophysical interactions given that the DST ring current is produced as a result of solar particle streams [16] , and it also has direct correlations with the geomagnetic field. Furthermore, there are a number of complex relationships previously noted between various sources of solar activity and geomagnetic fluctuations [17] . Given the large number of solar factors is found to have potential relationships with geomagnetic activity, it would be beneficial to identify an optimal statistical model for forecasting geomagnetic storms based on a simple subset of input variables. This would allow for potential early warning systems to be placed in effect at relevant institutions regarding future geomagnetic perturbations.
2. Methods
2.1. Geomagnetic and Solar Data
A number of predictive models were constructed using varying statistical methods of both linear and nonlinear processes. In each, the disturbance storm time (DST) index was used as the target variable to be predicted, while a number of solar wind and interplanetary magnetic field (IMF) measures were employed as independent variables (Bx, By, and Bz components of the IMF in nT, solar wind proton density in N·cm−3, solar wind plasma speed in km·s−1, and plasma flow pressure in nPa). A total of N = 1460 daily averages were obtained from January 1, 2009 to December 31, 2012. All data was obtained from the GSFC (Goddard Space Flight Center)/SPDF (Space Physics Data Facility) OMNIWeb interface (http://omniweb.gsfc.nasa.gov/).
2.2. Statistical Models
Five separate models were computed with varying forms of artificial neural network (ANN) and regression analyses using both Matlab 2011a and SPSS 17 software.
An ANN was constructed using Matlab in order to produce a nonlinear autoregressive network with exogenous input (NARX). DST index was entered as the target variable with 6 feedback delays specified for the autoregressive function, and 6 input delays also specified for the exogenous input. A single hidden layer was deemed adequate for this particular problem with 10 hidden neurons (HN) specified (Figure 3). Data was segmented into three sets using the divide block function in order to maintain temporal characteristics of the time series. A total of 70% was allocated for training, with 15% of cases used in both validation and testing trials. Neural network learning was limited to a maximum of 1000 epochs a priori. Initial neural weights were randomized. Two training algorithms were employed for comparison between Bayesian regularization (BRANN) and Levenberg Marquardt (LMANN).
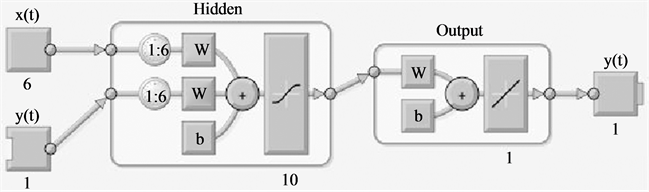
Figure 3. NARX network architecture; input layer consisting of x (6 variable exogenous input time series) and y (single variable autoregressive time series), 6 exogenous input delays and 6 feedback delays, 10 hidden layer neurons with single bias node and sigmoid activation function, single target (output) time series y.
A third variation of non-autoregressive ANN was constructed using SPSS Multilayer Perceptron (MLPANN) module with sigmoid hidden and output layer activation functions (Equation (1)). Network hidden layer architecture was constructed according to previous specifications obtained in Matlab (single hidden layer, 10 HN), with 70% of cases allocated to training and the remaining 30% used for testing.
For linear comparison, regression analyses were conducted using both full variable and stepwise variable entry.
3. Results
3.1. NARX: Bayesian Regularization
A NARX neural network constructed with Matlab software using a BRANN algorithm converged upon a solution after the maximum allowed number of iterations (1000). There were no significant error crosscorrelation or autocorrelation issues identified (e.g., Figure 4). The Bayesian method obtained highly significant (p < 0.001) correlations between output and target data (Figure 5; r = 0.918, rho = 0.84).
3.2. NARX: Levenberg Marquardt
Matlab was again utilized and a secondary NARX network was constructed by substituting the previous training with a LMANN algorithm. Again, there were no error crosscorrelation or autocorrelation issues identified. This particular network revealed significant (p < 0.001) correlations between target and output data (Figure 6; r = 0.732, rho = 0.747), although not as strong as that obtained using BRANN.

Figure 4. BRANN error (target-output) autocorrelation.
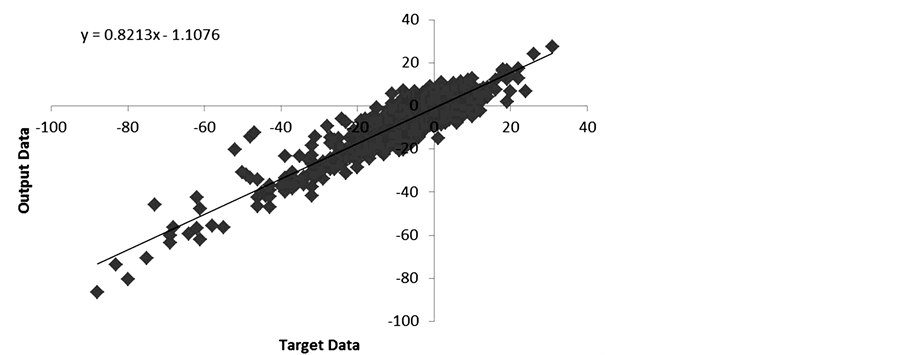
Figure 5. Correlation between original (target) and predicted (output) DST index values obtained with BRANN.
3.3. Non-Autoregressive: Multilayer Perceptron
Using a non-autoregressive neural network, MLPANN was used to predict DST index based solely on the input and hidden layers. This particular method revealed a significant correlation (p < 0.001) closer to that found with the LMANN analysis (Figure 7; r = 0.706, rho = 0.663). Additional independent importance analysis revealed that the Bz component of the IMF and solar wind proton density had the greatest connection to the output layer (Figure 8).
3.4. LR Enter
A linear regression (LR) was performed for further comparison of statistical predictive power. The first model was obtained by entering all predictor variables. A significant regression was revealed (F(6,1459) = 165.295, p < 0.001, adj. R2 = 0.403). The Durbin Watson statistic (0.935) indicated minute potential autocorrelations in the data (Figure 9). All variance inflation factors were < 10 suggesting no issues of multicollinearity. Significant correlations (p < 0.001) were obtained between target and predicted values (Figure 10; r = 0.637, rho = 0.634), but the relationship identified was reduced in power compared to ANN methods.
3.5. LR Stepwise
A secondary LR analysis was conducted using a stepwise method of variable entry for theoretically improved

Figure 6. Correlation between original (target) and predicted (output) DST index values obtained with LMANN.
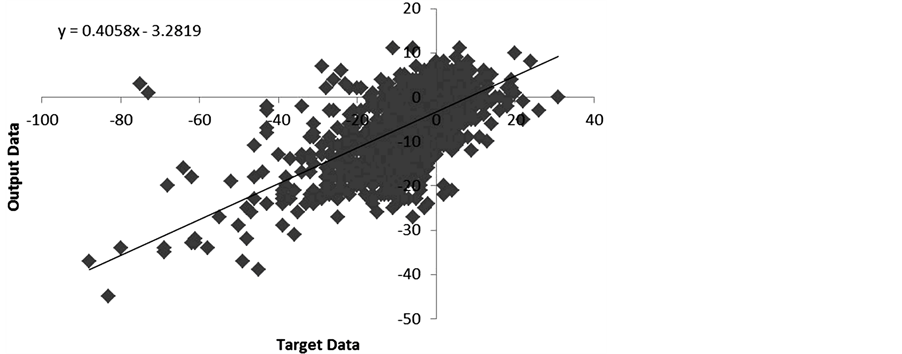
Figure 7. Correlation between original (target) and predicted (output) DST index values obtained with MLPANN.

Figure 8. Independent importance of each input variable as related to the connection with DST index.

Figure 9. Potential weak autocorrelation in regression model (LR enter).

Figure 10. Correlation between original (target) and predicted (output) DST index values obtained with LR enter.
accuracy of results. The only predictor variables to enter the equation were plasma speed and the Bz component of the IMF. A significant regression was identified (F(2,1459) = 458.729, p < 0.001, adj. R2 = 0.386), although the Durbin Watson statistic (0.933) again suggested potential data autocorrelations (Figure 11). There were no issues of multicollinearity according to the variance inflation factor statistics (all VIF < 10). Again, significant correlations (p < 0.001) were obtained between target and predicted data (Figure 12; r = 0.622, rho = 0.622), which were also reduced in coefficient strength compared to ANN methods.
3.6. Fit Comparisons
A Fisher r to z transformation (Equation (4)) was applied to pairings of correlation coefficients and compared using a simple z test (Equation (5)) in order to determine significant (Equation (6)) differences in final output of each model.
 (4)
(4)
 (5)
(5)
 (6)
(6)
The BRANN model prediction correlation was significantly greater (p < 0.0001) than LMANN (z = 17.35), MLPANN (z = 18.81), LR enter (z = 22.21), and LR stepwise (z = 22.88). LMANN and MLPANN methods did not differ significantly (z = 1.45, p > 0.05). However, the LMANN algorithm prediction coefficients were significantly greater (p < 0.0001) than both LR enter (z = 4.85) and LR stepwise (z = 5.52). MLPANN method also revealed predictive coefficients which were greater (p < 0.0001) than both LR enter (z = 3.4) and LR stepwise (z = 4.07).

Figure 11. Potential autocorrelation in regression model (LR stepwise).

Figure 12. Correlation between original (target) and predicted (output) DST index values obtained with LR stepwise.
3.7. Average Accuracy
Overall measures of performance error (target-output) were obtained as the root mean squared error (RMSE) of each model and were similarly reflective of a clear hierarchy in model accuracy, the values of which are summarized in Table 1. These results suggest that neural network methods produce a greater predictive capacity for both fit and accuracy in the context of DST index and solar winds compared to more traditional regression methods, while the Bayesian regularization (BRANN) algorithm was superior to other variations of ANN (Figure 13). This method was far more accurate regarding both the direction and magnitude of target values as demonstrated by the clear distinctive features shown in Figure 14 and Figure 15.
Table 1. Fit (r) and performance error (RMSE) of each statistical model.
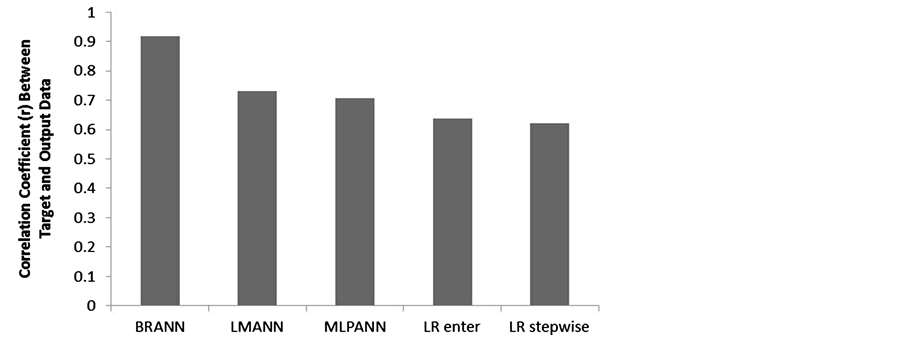
Figure 13. Correlation coefficients (r) for predictive fit of each model.
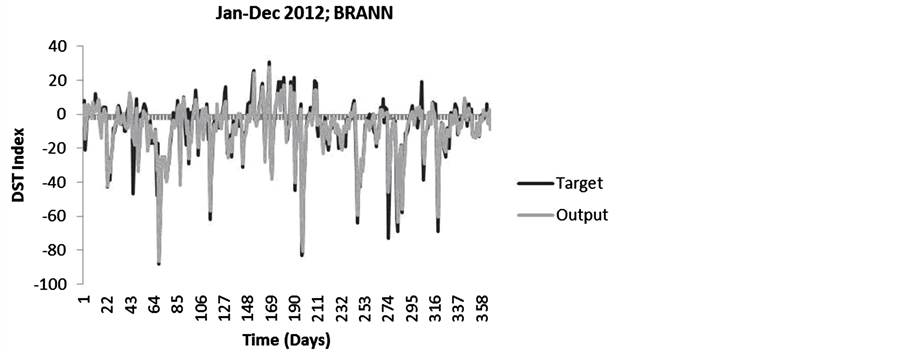
Figure 14. Target (original) and output (predicted) DST index values for 2012 using the BRANN algorithm.
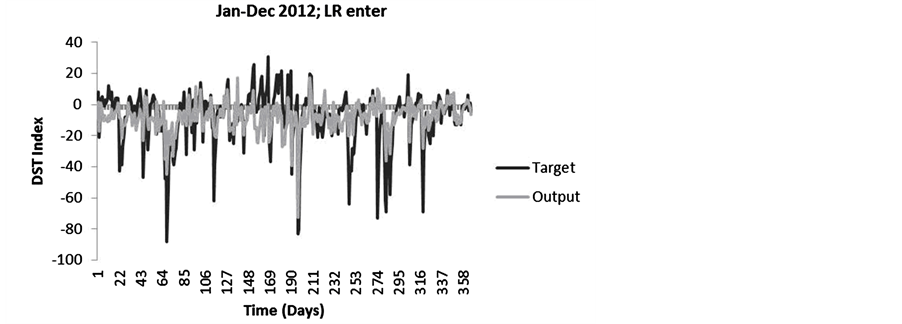
Figure 15. Target (original) and output (predicted) DST index values for 2012 using linear regression (enter all variables).
4. Conclusions
The results of this analysis appear to confirm those from a number of previous studies which have suggested that ANN models are more accurate compared to simple regressions for many applications [18] [19] . While the NARX models used relied on past values of the DST index, there was a significantly greater target to output fit apparently for the MLPANN network compared to regression analyses, which did not utilize DST feedback. There was a clear hierarchy of statistical models in the present analyses indicated by both fit (r) and overall accuracy (RMSE), and models from greatest to least relative fit/accuracy were BRANN, LMANN, MLPANN, LR enter, LR stepwise.
The Bayesian regularization algorithm for neural network training has previously been implicated as a superior model compared to other network algorithms [10] . This appears to be the case in the context of DST autoregressive prediction with solar wind input. It is clear that Bayesian probabilities are well suited to neural network learning for DST forecasting given the adaptive neural weights updated over the course of network construction based on new probabilities. Furthermore, regression models typically require a priori knowledge of variable interactions for accurate forecast implementation, while neural networks are capable of learning from an array of related measures and producing a highly accurate model. Standard regression models also tend to ignore non-linear effects which may be present, particularly in noisy datasets, or time series data with no clear linear relationship. It may also be important to note that the NARX model is capable of both open and closed loop performance and can be used to predict a step beyond an available dataset with associated performance measures. However, there are clear benefits to employ a range of statistical methods when interpreting complex interactions in order to gain a fuller picture of the system in question.
It is also interesting to note that the Bz component of the IMF was consistently identified as the greatest shared source of variance with geomagnetic disturbances, along with the speed and proton density of solar winds. This assemblage of contributing factors has previously been identified in the context of geomagnetic activity including Bz, particle density, and velocity of solar winds with DST index [20] . Modelling of DST variations was later examined using more complex methods of data transformation and analysis on a wider array of input measures [3] .
In the present study, the effects of solar wind variations are demonstrated using a range of input measures and statistical methods, which clearly demonstrate the enhanced potential for ANN models compared to more traditional statistical methods. Prior analyses also suggested that network performance improved with the addition of a greater range of IMF variables (e.g., Bx, By, Bz), which was also previously suggested by Boynton et al. [3] . However, network performance was reduced in magnitude with the addition of solar wind temperature in the input layer. The NARX networks still managed to outperform other models using untransformed variables of simple daily averages. Additionally, all data is freely available from an online source (http://omniweb.gsfc.nasa.gov/) open to any researcher interested in constructing models relevant to their own location.
Similarly, local forecasting with ANNs has proven effects in a number of areas and may be useful for predicting a range of events. Accurate modelling of solar and geomagnetic interactions is a particularly useful endeavor when the increasing reliance on technology civilization has reached. Given the known effects of geomagnetic storms on electrical systems, and even the significant effects of small geomagnetic perturbations on neurophysiology [13] , monitoring and forecasting of this phenomenon are increasingly vital. This is particularly prominent for satellite systems outside of the planetary atmosphere which may be quite sensitive to variations in ring current activity.
That powerful statistical software which is widely available is also a tremendous boon to statistical modelling and related research endeavors, and the complicated computations required for ANN methods are now easily employed in standard mathematical software, making relatively intimidating methods more accessible to the average researcher. Neural network predictions can be very powerful tools for both local and global predictions and can potentially be used to improve traditional models. ANN methods should be further investigated for potential applicability in better prediction of geomagnetic variations and storm level events, as well as to further elucidate the complex interconnections between solar and geophysical parameters.
Acknowledgements
The author would like to thank Dr. Michael Persinger, Nicolas Rouleau, Lucas Tessaro, David Vares, Dr. Blake Dotta, and Prof. Kevin Saroka for valuable feedback and support. Additional thanks to Dr. Natalia Papitashyili for maintaining the NASA OMNIWeb database. Funding for this research was provided by Dr. Michael Persinger.
References
- Erguo, L. and Jinshou, Y. (2002) An Input-Training Neural Network Based Nonlinear Principal Component Analysis Approach for Fault Diagnosis. Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, 10-14 June 2002, 2755-2759.
- Mehrotra, K., Mohan, C.K. and Ranka, S. (1997) Elements of Artificial Neural Networks. MIT Press, Cambridge.
- Boynton, R.J., Balikhin, M.A., Billings, S.A. and Amariutei, O.A. (2013) Application of Nonlinear Autoregressive Moving Average Exogenous Input Models to Geospace: Advances in Understanding and Space Weather Forecasts. Annales Geophysicae, 31, 1579-1589. http://dx.doi.org/10.5194/angeo-31-1579-2013
- Khan, J., Wei, J.S., Ringner, M., Saal, L.H., Ladanyi, M., Westermann, F., Berthold, F., Schwab, M., Antonescu, C.R., Peterson, C. and Meltzer, P.S. (2001) Classification and Diagnostic Prediction of Cancers Using Gene Expression Profiling and Artificial Neural Networks. Nature Medicine, 7, 673-679. http://dx.doi.org/10.1038/89044
- Looney, C.G. (1997) Pattern Recognition Using Neural Networks: Theory and Algorithms for Engineers and Scientists. Oxford University Press, Oxford.
- Widrow, B. and Lehr, M.A. (1990) 30 Years of Adaptive Neural Networks: Perceptron, Madaline, and Backpropagation. Proceedings of the IEEE, 78, 1415-1442. http://dx.doi.org/10.1109/5.58323
- Leonard, J. and Kramer, M.A. (1990) Improvement of the Backpropagation Algorithm for Training Neural Networks. Computers & Chemical Engineering, 14, 337-341. http://dx.doi.org/10.1016/0098-1354(90)87070-6
- Levenberg, K. (1944) A Method for the Solution of Certain Non-Linear Problems in Least Squares. Quarterly of Applied Mathematics, 2, 164-168.
- Mahinthakumar, G. and Sayeed, M. (2005) Hybrid Genetic Algorithm: Local Search Methods for Solving Groundwater Source Identification Inverse Problems. Journal of Water Resources Planning and Management, 131, 45-57. http://dx.doi.org/10.1061/(ASCE)0733-9496(2005)131:1(45)
- Burden, F. and Winkler, D. (2008) An Empirical Relationship between Interplanetary Conditions and DST. Methods in Molecular Biology, 458, 25-44.
- Menezes Jr., J.M.P. and Barreto, G.A. (2008) Long-Term Time Series Prediction with the NARX Network: An Empirical Evaluation. Neurocomputing, 71, 3335-3343. http://dx.doi.org/10.1016/j.neucom.2008.01.030
- Oliveira, A.G., Silva, M.R., Echer, E., Dal Lago, A., Braga, C.R., Mendonca, R.R.S., Schuch, N.J., Munakata, K. and Kuwabara, T. (2013) Simulations of the Interplanetary Magnetic Field Conditions with NARX Networks. 33rd International Cosmic Ray Conference, the Astroparticle Physics Conference, Rio de Janeiro, 2-9 July 2013.
- Saroka, K.S., Caswell, J.M., Lapointe, A. and Persinger, M.A. (2013) Greater Electroencephalographic Coherence between Left and Right Temporal Lobe Structures during Increased Geomagnetic Activity. Neuroscience Letters, 560, 126-130.
- Boteler, D.H. (2001) Assessment of Geomagnetic Hazard to Power Systems in Canada. Natural Hazards, 23, 101-120. http://dx.doi.org/10.1023/A:1011194414259
- Mulligan, B.P., Hunter, M.D. and Persinger, M.A. (2010) Effects of Geomagnetic Activity and Atmospheric Power Variations on Quantitative Measures of Brain Activity: Replication of Azerbaijani Studies. Advances in Space Research, 45, 940-948. http://dx.doi.org/10.1016/j.asr.2009.12.008
- Leske, R.A., Cummings, J.R., Mewaldt, R.A., Stone, E.C. and von Rosenvinge, T.T. (1995) Measurements of the Ionic Charge States of Solar Energetic Particles Using the Geomagnetic Field. The Astrophysical Journal Letters, 452, 149.
- Zhang, J., Richardson, I.G., Webb, D.F., Gopalswamy, N., Huttunen, E., Kasper, J.C., Nitta, N.V., Poomvises, W., Thompson, B.J., Wu, C.C., Yashiro, S. and Zhukov, A.N. (2007) Solar and Interplanetary Sources of Major Geomagnetic Storms (DST ≤ −100 nT) during 1996-2005. Journal of Geophysical Research: Space Physics, 112.
- Jefferson, M.F., Pendleton, N., Lucas, S.B. and Horan, M.A. (1997) Comparison of a Genetic Algorithm Neural Network with Logistic Regression for Predicting Outcome after Surgery for Patients with Nonsmall Cell Lung Carcinoma. Cancer, 79, 1338-1342.
- Eftkhar, B., Mohammad, K., Eftekhar Ardebili, H., Ghodsi, M. and Ketabchi, E. (2005) Comparison of Artificial Neural Network and Logistic Regression Models for Prediction of Mortality in Head Trauma Based on Initial Clinical Data. BMC Bioinformatics and Decision Making, 5, 3.
- Lundstedt, H., Gleisner, H. and Wintoft, P. (2002) Operational Forecasts of the Geomagnetic DST Index. Geophysical Research Letters, 29, 34-1-34-4. http://dx.doi.org/10.1029/2002GL016151


