Journal of Signal and Information Processing
Vol. 4 No. 1 (2013) , Article ID: 28277 , 9 pages DOI:10.4236/jsip.2013.41003
Denoising of Medical Images Using Multiwavelet Transforms and Various Thresholding Techniques
![]()
1Department of Computer Engineering, College of Computer Engineering & Science, Salman bin Abdulaziz University, Al-Kharj, Saudi Arabia; 2Department of Electronics & Communication Engineering, Lords Institute of Engineering & Technology, Hyderabad, India.
Email: syedamjadali.lords@gmail.com
Received August 6th, 2012; revised September 24th, 2012; accepted October 16th, 2012
Keywords: Multiwavelets; Noise; Thresholding; Additive White Gaussian Noise; Signal-to-Noise Ratio; Discrete Multiwavelet Transforms; Chui Lian; Symmetric Asymmetric Multiwavelet Transform; Bi-Hermite Multiwavelet Transform; Modified Universal Thresholding
ABSTRACT
The problem of estimating an image corrupted by additive white Gaussian noise has been of interest for practical reasons. Non-linear denoising methods based on wavelets, have become popular but Multiwavelets outperform wavelets in image denoising. Multiwavelets are wavelets with several scaling and wavelet functions, offer simultaneously Orthogonality, Symmetry, Short support and Vanishing moments, which is not possible with ordinary (scalar) wavelets. These properties make Multiwavelets promising for image processing applications, such as image denoising. The aim of this paper is to apply various non-linear thresholding techniques such as hard, soft, universal, modified universal, fixed and multivariate thresholding in Multiwavelet transform domain such as Discrete Multiwavelet Transform, Symmetric Asymmetric (SA4), Chui Lian (CL), and Bi-Hermite (Bih52S) for different Multiwavelets at different levels, to denoise an image and determine the best one out of it. The performance of denoising algorithms and various thresholding are measured using quantitative performance measures such as, Mean Square Error (MSE), and Root Mean Square Error (RMSE), Signal-to-Noise Ratio (SNR), Peak Signal-to-Noise Ratio (PSNR). It is found that CL Multiwavelet transform in combination with modified universal thresholding has given best results
1. Introduction
Digital images play an important role both in daily life applications such as satellite television, Magnetic Resonance Imaging (MRI), computer tomography as well as in areas of research and technology such as geographical information systems and astronomy. Data sets collected by image sensors are generally contaminated by noise. Imperfect instruments, problems with the data acquisition process, and interfering natural phenomena can all degrade the data of interest. Furthermore, noise can be introduced by transmission errors and compression. Thus, denoising is often a necessary and the first step to be taken before the image data is analysed. It is necessary to apply an efficient denoising technique to compensate for such data corruption. Image denoising still remains a challenge for researchers because noise removal introduces artifacts and causes blurring of the images. This paper describes different methodologies for noise reduction giving an insight as to which algorithm should be used to find the most reliable estimate of the original image data, given its degraded version. Noise modeling in images is greatly affected by capturing instruments, data transmission media, image quantization and discrete sources of radiation. Different algorithms are used depending on the noise model. Most of the natural images are assumed to have additive random noise which is modeled as a Gaussian.
The developments in wavelet theory have given rise to the wavelet thresholding method, for extracting an image from noisy data. Multiwavelets, wavelets with several scaling functions, have recently been introduced and they offer simultaneous orthogonality, symmetry and short support, which is not possible with ordinary wavelets, also called scalar wavelets. This property makes Multiwavelets more suitable for various image processing applications, especially denoising.
Donoho and Johnstone pioneered the theoretical formalization of filtering additive white Gaussian noise (of zero mean and standard deviation) via thresholding the decomposed coefficients. A decomposed coefficient is subjected to a given threshold and is set to zero if its magnitude is less than the threshold; otherwise, it is kept or modified, depending upon the thresholding rule. The choice of threshold determines to a great extent the efficiency of denoising algorithm.
Denoising procedure is depicted in Figure 1.
Step 1: Original image is a medical tomographic image (head phantom) to which noise components like additive white Gaussian noise is added to create a noisy image ![]()
![]()
![]()
![]() .
.
Step 2: Pre-filtering is done on the noisy image to convert the scalar coefficients of an image into vector coefficients for Multiwavelet decomposition.
Step 3: It deals with decomposition of pre-filtered image using various Multiwavelets like GHM, CL, SA4, BiHermite52S, and their respective Multiwavelet transforms.
Step 4: Thresholding methods are used to remove noise from decomposed image. Here we apply Multiwavelet thresholds such as soft, hard, universal, modified, fixed and multivariate thresholds.
Step 5: By applying inverse Multiwavelet transforms (IMWT), to thresholded coefficients, we get the denoised vector output image.
Step 6: Post filtering is done on reconstructed image to get back the denoised image coefficients in scalar form.
2. Theoretical Aspects of Multiwavelets
The idea of Multiwavelet originates from the generalization of scalar wavelets [1,2]. Instead of one scaling and one wavelet function, multiple scaling and multiple wavelet functions are used. This leads to more degree of freedom in constructing Multiwavelets. Therefore, opposed to scalar wavelets, properties such as orthogonality, symmetry, higher order of vanishing moments, compact support can be gathered simultaneously in Multiwavelets. Multiwavelets are of mainly two types: 1) Orthogonal type such as Geronimo-Hardin-Massopust (GHM), Symmetric Asymmetric (SA4), Chui-Lian (CL); and 2) BiOrthogonal type such as Bi-Orthogonal Hermite (Bih52S).
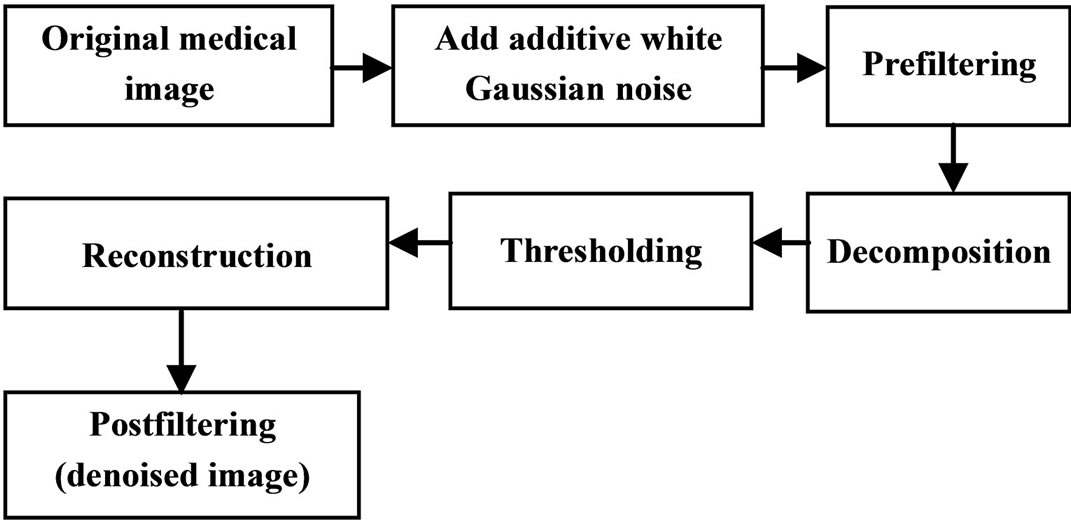
Figure 1. Block diagram of denoising using Multiwavelet transformation.
[3,4]. The scaling functions f1 and f2 are symmetric (linear phase) and they have short support (two intervals or less). The coefficients of Multiwavelets are 2 × 2 matrix. It retains the orthogonality of the Multiwavelets. The incoming signal is scalar type and is converted to vector type by using prefilter. The vector image is applied in discrete time to discrete Multiwavelet transform for low pass filtering, using low pass filter coefficients and down sampled (decimated) by 2, to get ck coefficients and high pass filter coefficients are used for high pass filtering and down sampled by two to get dk coefficients. This is the two band analysis bank. A perfect reconstruction synthesis bank recovers the image from the two down sampled outputs as shown in Figure 2 [5-7].
The sub-bands of a single level Multiwavelet decomposition is shown in Figure 3. It has 16 sub-bands of an image [8,9].
Multiwavelets are characterized with several scaling functions and associated wavelet functions as given in Equations (1) and (2) respectively [10-12].
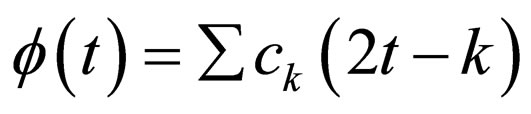 (1)
(1)
 (2)
(2)
where f(t) is a multiscaling function, W(t) is a Multiwavelet function.
A multi filter has two or more low pass filters. The purpose of this multiplicity is to achieve the following properties [1].
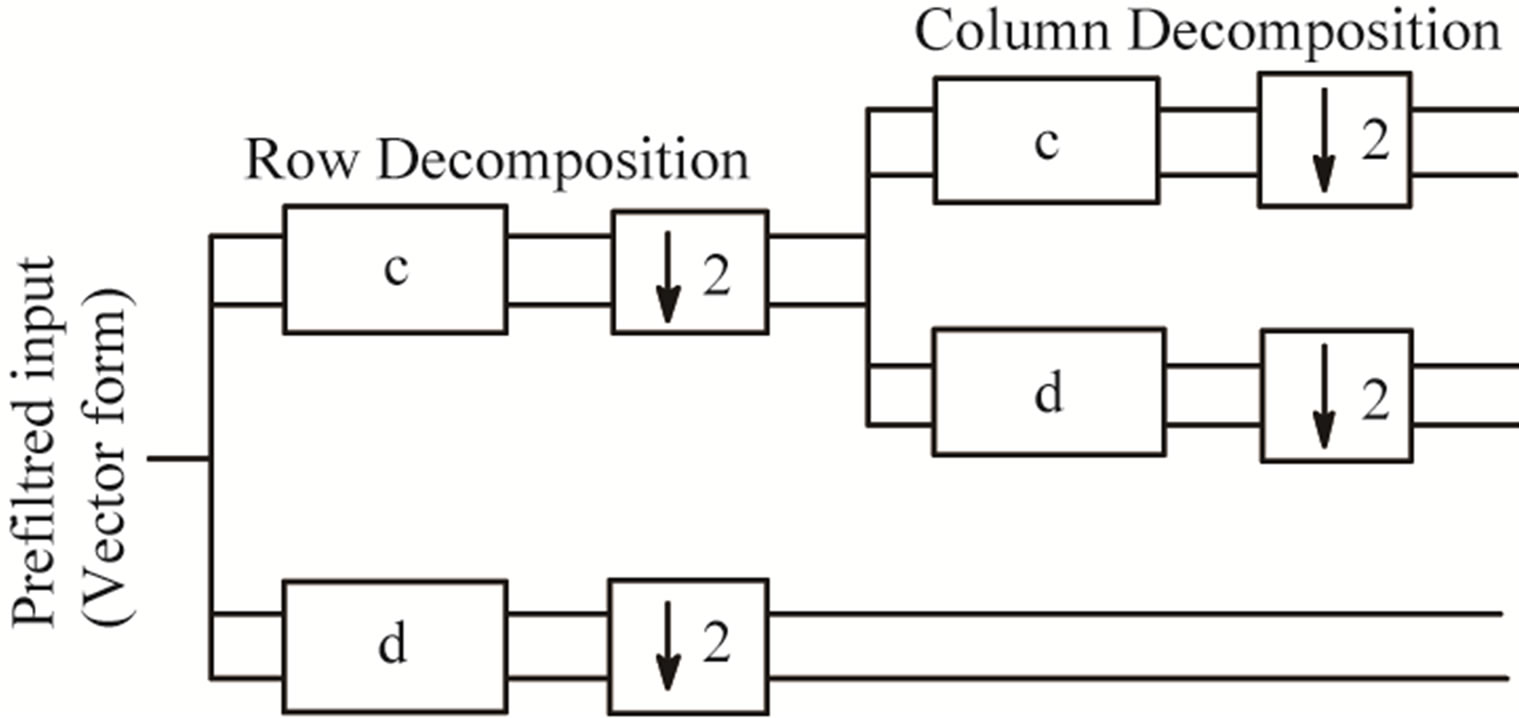
Figure 2. A multifilter bank with low pass filter iterated once.
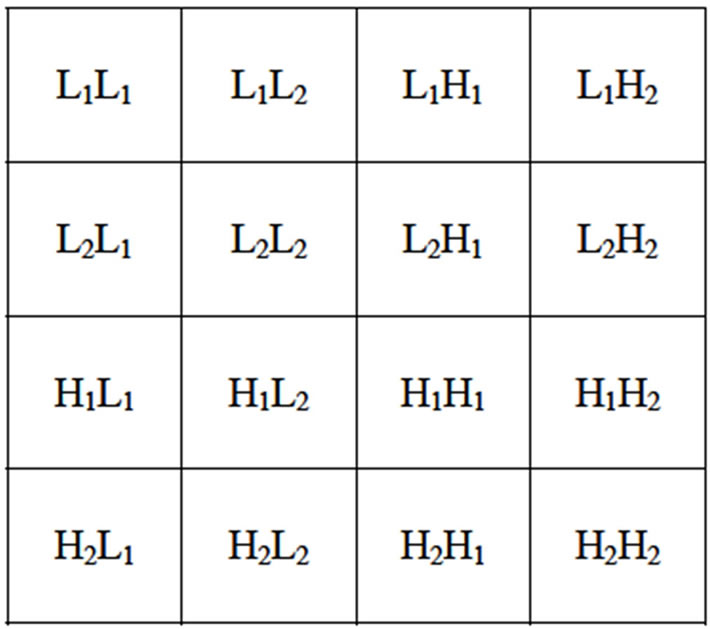
Figure 3. Image sub-bands after one level of Multiwavelet decomposition.
Properties of Φ1 and Φ2: [13-15]
1) Symmetry: f1 and f2 have linear phase, i.e., they are even functions (after a shift of the origin).
2) Short Support: Fi vanishes outside the interval [0, i]. Short support do not have much boundary problem. Long support must modify the function near boundaries. Wavelets have long support to achieve orthogonality. But Multiwavelets have short support and simultaneous orthogonality.
3) Second Order Accuracy: The scaling functions have second order accuracy, which establishes two vanishing moments.
4) Orthogonality: The translates 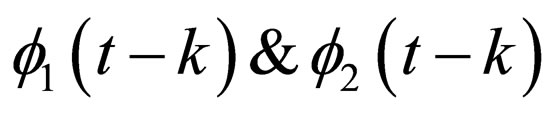 are all mutually orthogonal.
are all mutually orthogonal.
5) Matrix Multiscaling (Dilation) and Multiwavelet Equations: The coefficient “ck” and “dk” are 2 × 2 matrices multiplying vectors of scaling and wavelet functions as given in Equations (3) and (4) respectively.
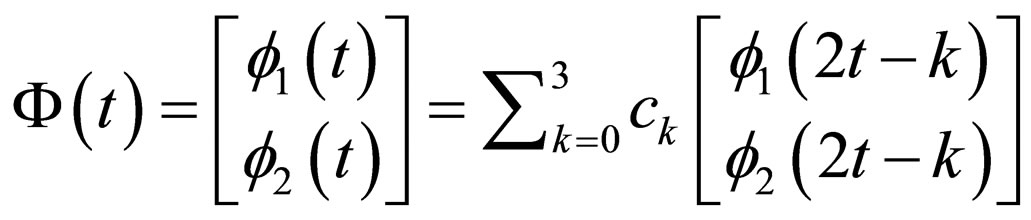 (3)
(3)
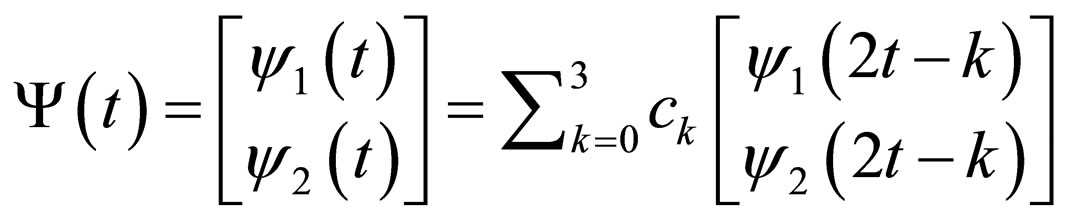 (4)
(4)
3. Thresholding Techniques
3.1. Hard Thresholding
It chooses coefficients greater than the given threshold λ and sets others to zero. It is unsuccessful in removing large noise coefficients.
The hard thresholding, operator is defined in Equation (5) as
 (5)
(5)
The transfer function of the same is shown in Figure 4.
If coefficient > λ, value attributes to original pixel, else its noise and we discard it.
3.2. Soft Thresholding
Soft thresholding yields smaller error than hard and is generally preferred over hard thresholding. Soft thresholding shrinks coefficients by the threshold λ towards zero. It is also called as shrinkage function. The soft thresholding operator is defined in Equation (6) as,
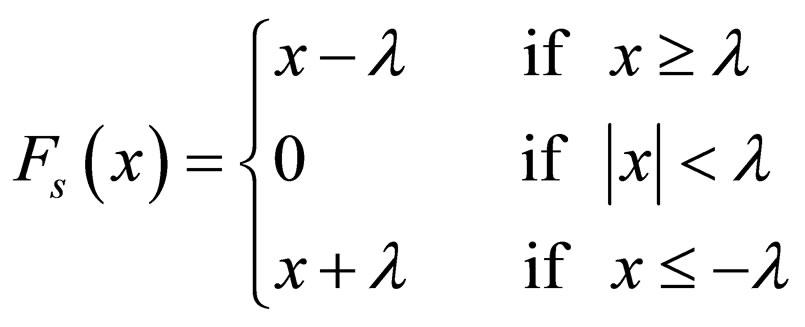 (6)
(6)
The transfer function of the same is shown in Figure 5.
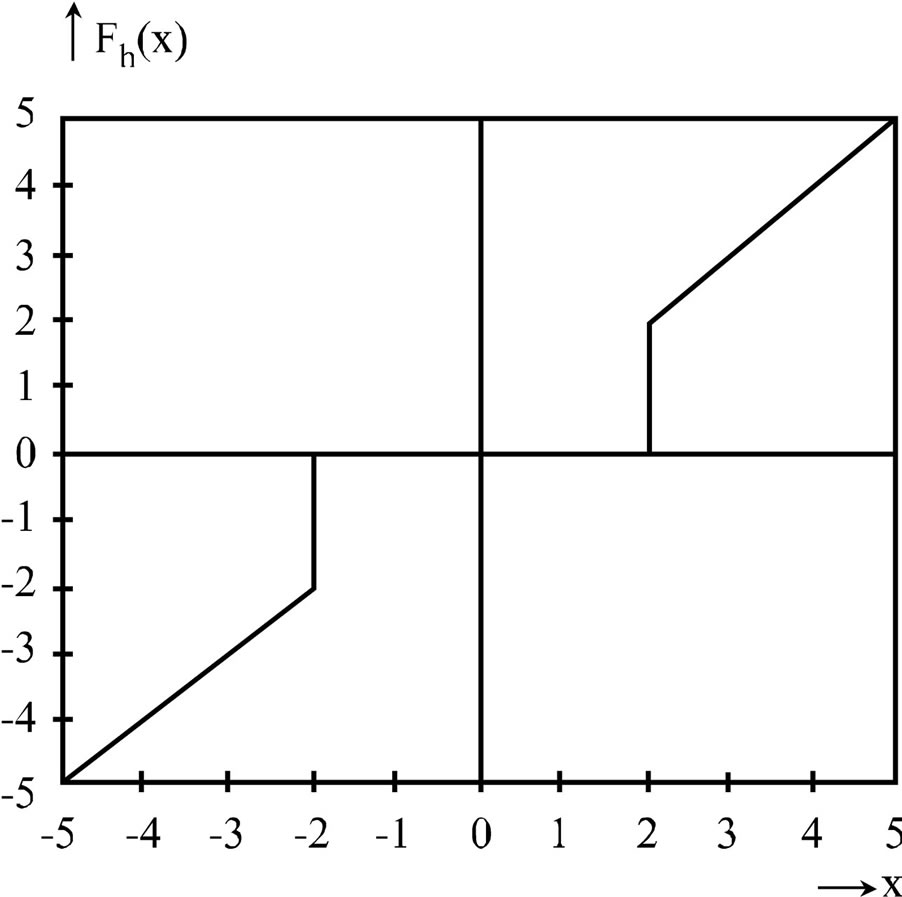
Figure 4. Hard thresholding.

Figure 5. Soft thresholding.
3.3. Wavelet Thresholding [16,17]
Noise is generally present in the higher order frequency components obtained after wavelet and Multiwavelet decomposition. wavelet thresholding is the estimation technique which exploits the capabilities of wavelet transforms. Here small coefficients dominated by noise are set to zero, when they are below a certain threshold. In this way, noise can be removed.
3.3.1. Universal Threshold
The Universal threshold was introduced by Donoho and Johnston for scalar wavelets. It is given in Equation (7) as,
 , (7)
, (7)
where σ is the standard deviation of the noise.
N is the sample size.
Same threshold is applied to all coefficients regardless of the decomposition level.
For images, N is chosen to be the number of pixels in a row rather than the total number of pixels in the image. It is observed that this choice for N results in higher SNR values.
3.3.2. Modified Universal Threshold
1) The modified universal threshold is given in Equation (8) as,
 , (8)
, (8)
where σ is the standard deviation of the noise. N is the sample size.
2) Another modified universal threshold is given in Equation (9) as,
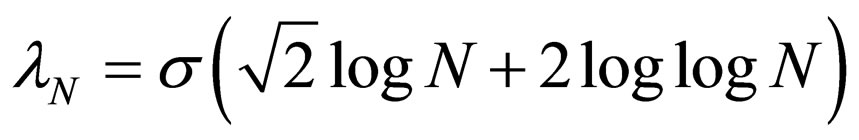 (9)
(9)
where N is the sample size.
3.3.3. New Thresholding
The new threshold is given in Equation (10) as,
 (10)
(10)
3.3.4. Multivariate Thresholding
This method is based on parent-child relationship which exists between image pixels of various sub-bands of Multiwavelet decomposition. If the parent coefficient has a small value, then the children would likely have small values. If the parent coefficient has a large value, the child might also have large values.
3.4. Measuring Parameters
3.4.1. Mean Square Error (MSE)
The MSE between the original image I(x,y) and the reconstructed image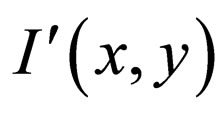 is given in Equation (11) as,
is given in Equation (11) as,
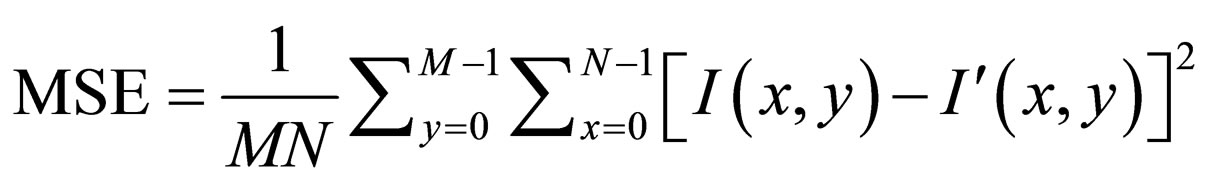 (11)
(11)
where I(x,y) is the original image, 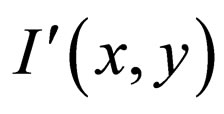 is the approximated version, which is actually the decompressed image and
is the approximated version, which is actually the decompressed image and 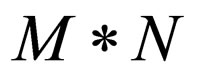 represents the size of an image.
represents the size of an image.
3.4.2. Signal-to-Noise Ratio (SNR)
It is another measure often used to compare the performance of reproduced images. It is given in Equation (12) as,
 (12)
(12)
3.4.3. Peak Signal-to-Noise Ratio (PSNR)
It is more subjective qualitative measurement of distortion. For 8-bit image, it is given in Equation (13) as,
 (13)
(13)
3.5. Experimental Results
The measuring parameters such as MSE, RMSE, PSNR and SNR values for various Multiwavelet transforms with repeated row prefilter and thresholding techniques are tabulated in Table 1.
3.5.1. Using Repeated Row Pre-Filtering Method
The measuring parameters such as MSE, RMSE, PSNR and SNR values for various Multiwavelet transforms with approximation prefilter and thresholding techniques are tabulated in Table 2.
3.5.2. Using Approximation Pre-Filtering Method
The measuring parameters such as MSE, RMSE, and PSNR and SNR values for GHM Multiwavelet transforms with various thresholding techniques are tabulated in Table 3.
The measuring parameters such as MSE, RMSE, and PSNR and SNR values for GHMAP Multiwavelet transforms with various thresholding techniques are tabulated in Table 4.
The measuring parameters such as MSE, RMSE, and PSNR and SNR values for CARDBAL2 Multiwavelet transforms with various thresholding techniques are tabulated in Table 5.
Denoising of tomographic image of phantom is shown in Figure 6.
Comparison of various Multiwavelet transformation with thresholding techniques with respect to parameters such as MSE, SNR, RMSE are depicted in the Figures 7-9 respectively.
Comparison of various measuring parameters before and after thresholding is depicted in Figure 10.
Comparison between various Multiwavelet transforms along with various thresholding techniques is given in Figure 11 and Comparison between various Multiwavelet transforms is given in Figure 12.
3.6. Conclusions
Multiwavelets became a focus of research partly because they made possible the construction of wavelet systems that are simultaneously orthogonal, symmetric and Finite Impulse Response. However, it has become clear that the implementation of the discrete Multiwavelet transform does not require prefilters. The performance of the Multiwavelets with different thresholding methods were investigated. We have as well modified a thresholding method to give better performance for the tomographic
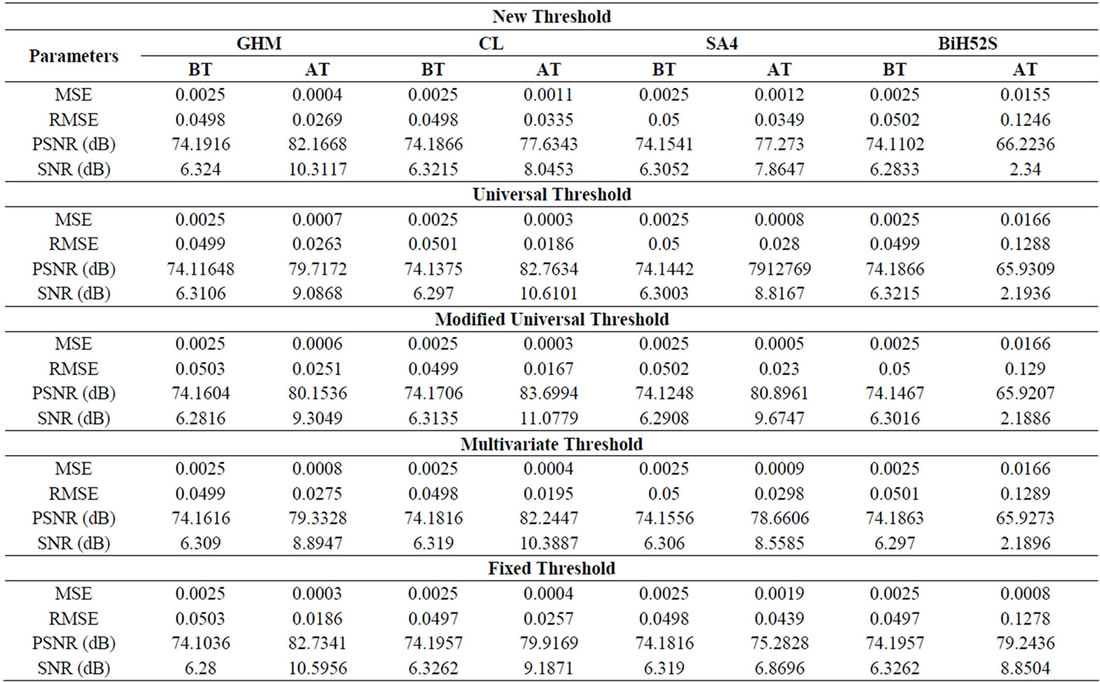
Table 1. Measurement of denoising parameters using various Multiwavelet transformation with repeated row prefilter and thresholding techniques.
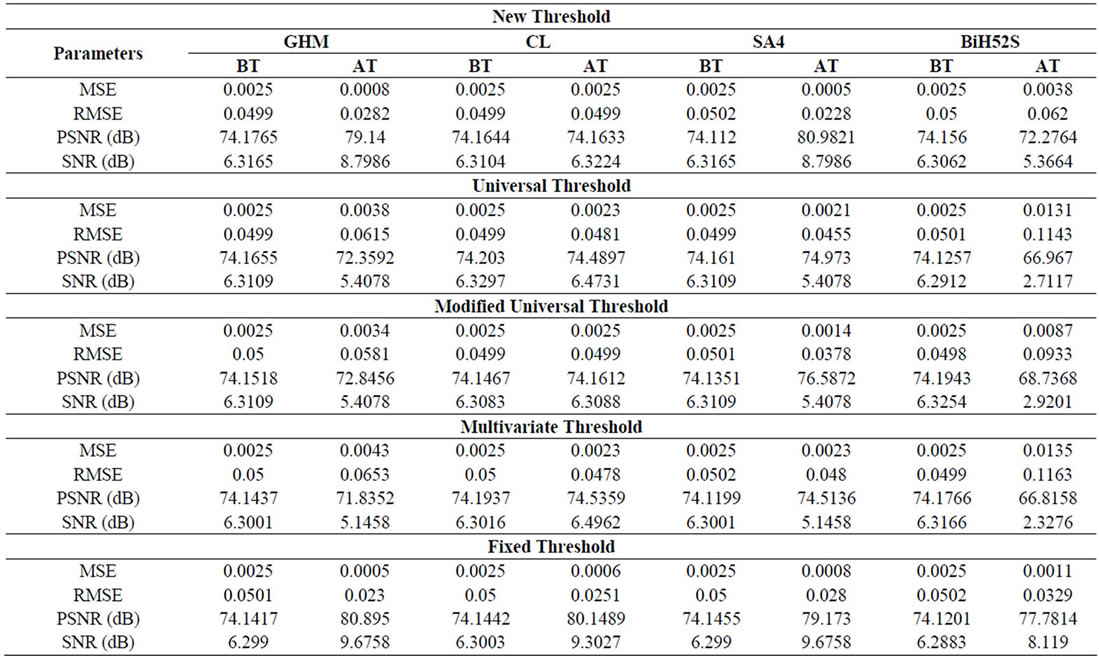
Table 2. Measurement of denoising parameters using various Multiwavelet transformation with approximation prefilter and thresholding techniques.

Table 3. Measurement of denoising parameters using direct Multiwavelet transform (GHM) using various thresholding techniques.

Table 4. Measurement of denoising parameters using direct Multiwavelet transform (GHMAP) using various thresholding.

Table 5. Measurement of denoising parameters using Multiwavelet transform (CARDBAL2) with identity prefilter using various thresholding.
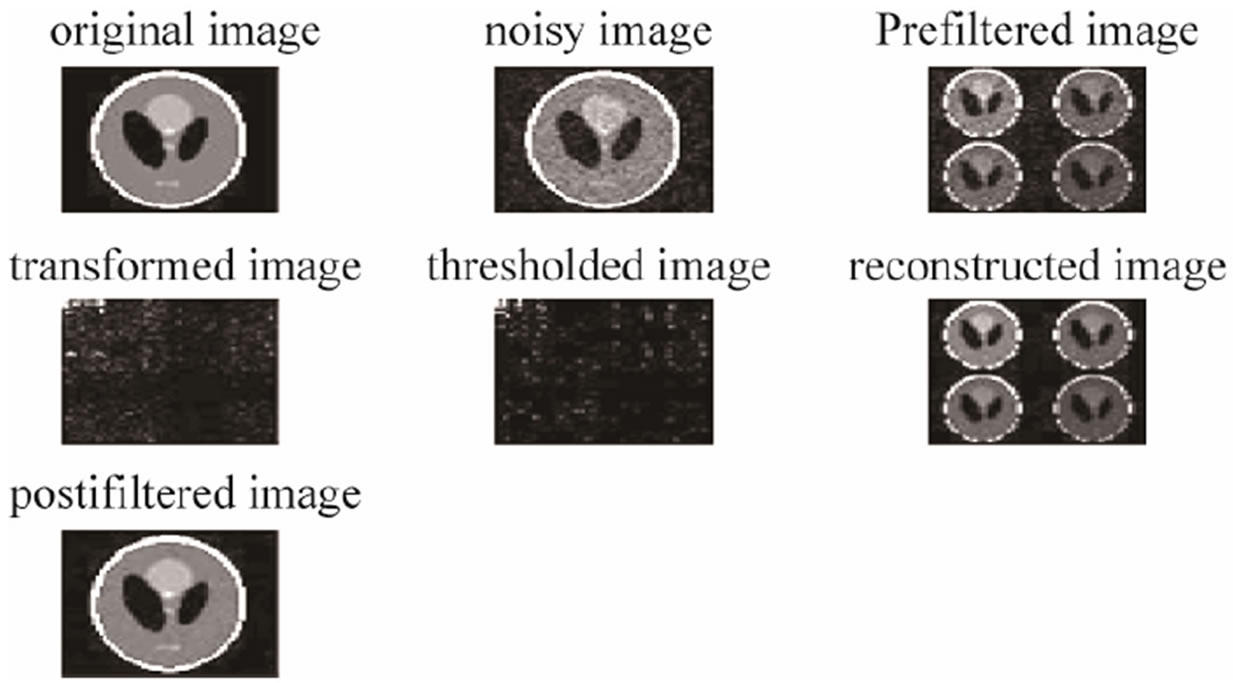
Figure 6. Denoising of a phantom using Multiwavelet transformation and thresholding techniques.
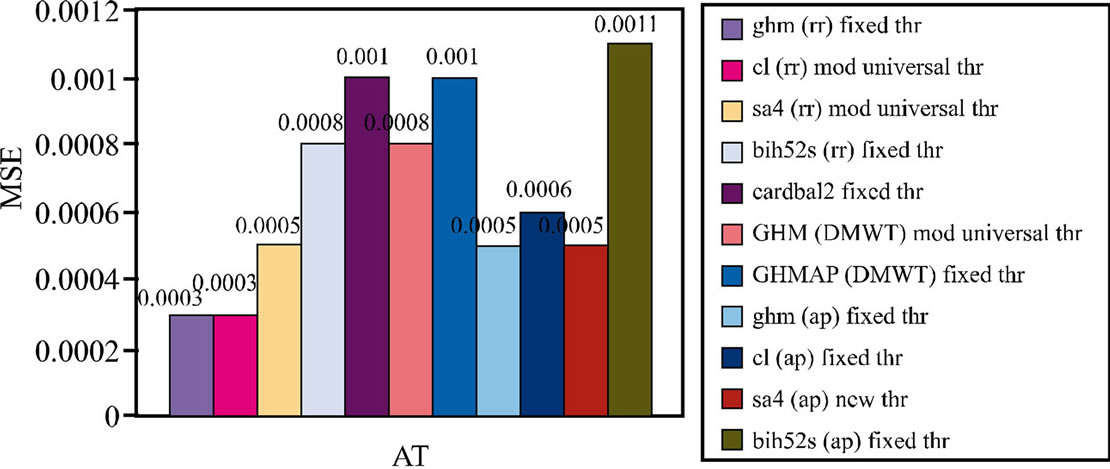
Figure 7. Comparison of various Multiwavelet transformation with thresholding techniques with respect to Mean Square Error.
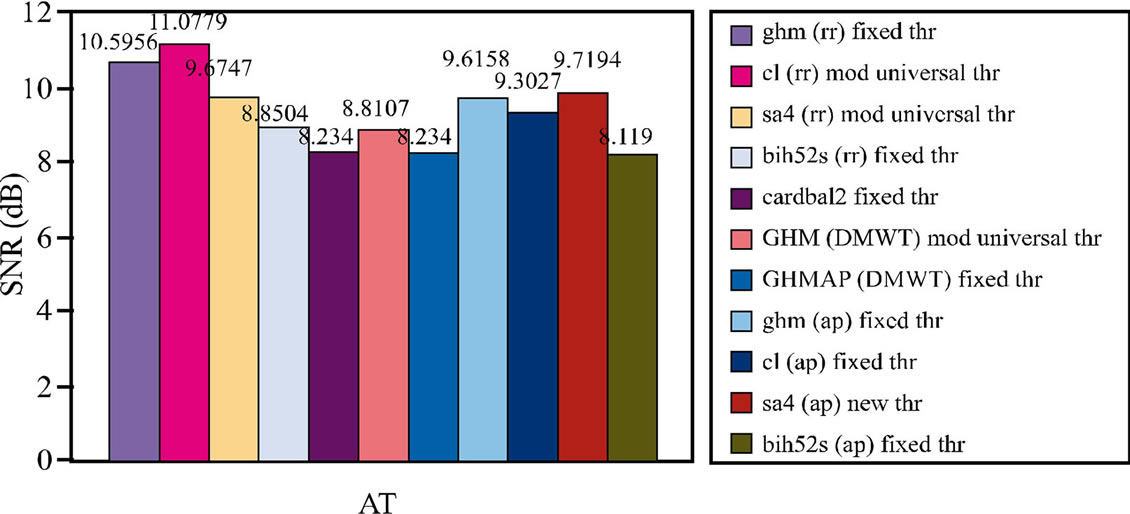
Figure 8. Comparison of various Multiwavelet transformation with thresholding techniques with respect to Signal-to-Noise Ratio.
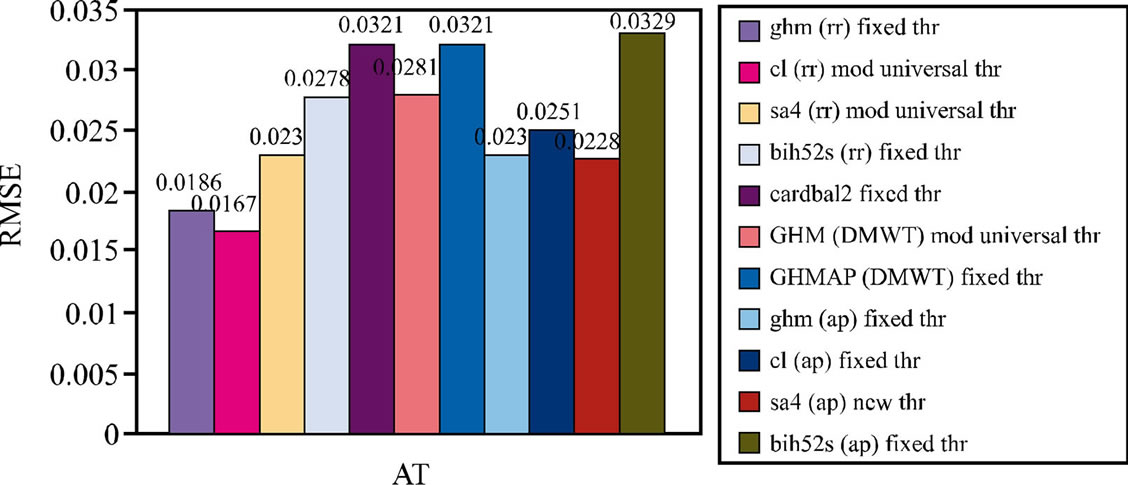
Figure 9. Comparison of various Multiwavelet transformation with thresholding techniques with respect to Root Mean Square Error.

Figure 10. Comparison of various measuring parameters before and after thresholding.
image used in our algorithms and named it as new threshold.
To test the effectiveness of our algorithm, we added Gaussian noise to the 256 × 256 gray image phantom to, get noisy image and then applied Multiwavelet transforms and thresholding techniques to obtain denoised image. In this paper, different Multiwavelets like GHM, SA4, CL Bi-Hermite., and Multiwavelet transforms like Dec_2D, GHM and GHMAP with approximation and repeated row prefilters and various thresholding techniques like universal threshold, modified universal threshold, new threshold, multivariate threshold and fixed threshold is used to denoise the test image. Noise estimation parameters such as Root Mean Square Error (RMSE), Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR) and Signal to Noise Ratio (SNR) are
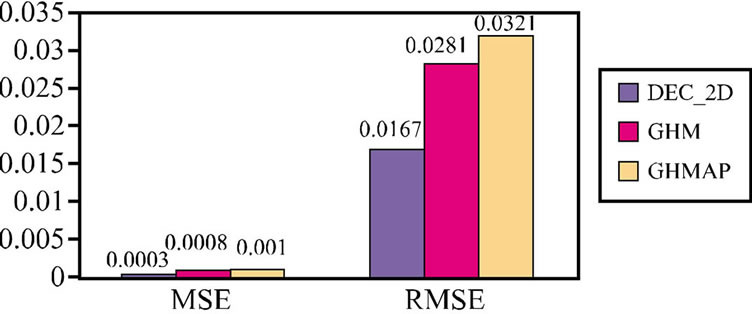
Figure 11. Comparison between various Multiwavelet transforms along with various thresholding techniques.

Figure 12. Comparison between various Multiwavelet transforms.
used to evaluate the performance of algorithm.
We have compared different Multiwavelets and thresholding techniques used. It is found that CL is the best Multiwavelet, when used with modified universal threshold and repeated row prefilter.
3.7. Future Scope
Nonetheless, there is always room for improvement. Since Multiwavelets are relatively a new subject of study, only a few construction methods for Multiwavelets are available. Most current filter available have two, three or fourth order of approximation. Future construction methods may add even higher order of approximation, while preserving the desirable features of current methods, would most likely result in multifilters that perform even better in image denoising and compression applications. Moreover the Multiwavelet systems available presently have the multiscaling and Multiwavelet coefficients which are 2 × 2 matrices. There is a possibility that in future many more Multiwavelet systems might be developed with matrix coefficients with higher order, which could provide even better results in the field of image denoising.
REFERENCES
- G. Strang and V. Strela, “Short Wavelets and Matrix Dilation Equations,” IEEE Transactions on Signal Processing, Vol. 43, No. 1, 1995, pp. 108-115. doi:10.1109/78.365291
- G. Strang and V. Strela, “Orthogonal Multiwavelets with Vanishing Moments,” Journal of Optical Engineering, Vol. 33, No. 7, 1994, pp. 2104-2107. doi:10.1117/12.172247
- V. Strela, P. N. Heller, G. Strang, P. Topiwala and C. Heil, “The Application of Multiwavelet Filterbanks to Image Processing,” IEEE Transactions on Image Processing, Vol. 8, No. 4, 1999, pp. 548-563.
- V. Strela, and A. T. Walden, “Signal and Image Denoising via Wavelet Thresholding: Orthogonal and Biorthogonal, Scalar and Multiple Wavelet Transforms,” Statistic Section Technical Report TR-98-01, Department of Mathematics, Imperial College, London, 1998.
- B. R. Johnson, “Multiwavelet Moments and Projection Prefilters,” IEEE Transactions on Signal Processing, Vol. 48, No. 11, 2000, pp. 3100-3108.
- C. K. Chui and J. A. Lian, “A Study of Orthogonal Multiwavelets,” Applied Numerical Mathematics, Vol. 20, No. 3, 1996, pp. 273-298. doi:10.1016/0168-9274(95)00111-5
- D. P. Hardin and D. W. Roach, “Multiwavelet Prefilters-I: Orthogonal Prefilters Preserving Approximation Order P ≤ 2,” IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, Vol. 45, No. 8, 1998, pp. 1106-1112.
- T. R. Downie and B. W. Silverman, “The Discrete Multiple Wavelet Transform and Thresholding Methods,” IEEE Transactions on Signal Processing, Vol. 46, No. 9, 1998, pp. 2558-2561.
- J. Y. Tham, L. X. Shen, S. L. Lee and H. H. Tan, “A General Approach for Analysis and Application of Discrete Multiwavelet Transforms,” IEEE Transactions on Signal Processing, Vol. 48, No. 2, 2000, pp. 457-464.
- K. Attakitmongcol, D. P. Hardin and D. M. Wilkes, “Multiwavelet Prefilters-Part II : Optimal Orthogonal Prefilters,” IEEE Transactions of Image Processing, Vol. 10, No. 10, 2001, pp. 1476-1487.
- G. Andria, F. Attivissimo, G. Cavone, M. Spadavecchia and T. Magli, “Denoising Filter to Improve the Quality of CT Images,” Proceedings of IEEE Conference on Instrumentation and Measurement Technology, 5-7 May 2009, pp. 947-950.
- L. X. Shen, H. H. Tan and J. Y. Tham, “Some Properties of Symmetric-Antisymmetric Orthonormal Multiwavelets,” IEEE Transactions on Signal Processing, Vol. 48, No. 7, 2000, pp. 2161-2163.
- V. Strela and A. T. Walden, “Orthogonal and Biorthogonal Multiwavelets for Signal Denoising and Image Compression,” Proceedings of SPIE, Vol. 3391, 1998, pp. 96-107. doi:10.1117/12.304924
- X. G. Xia, J. Geronimo, D. Hardin and B. Suter, “On Computations of Multiwavelets Transforms,” Proceedings of SPIE, San Diego, July 1995.
- X.-G. Xia, J. Geronimo, D. Hardin and B. Suter, “Design of Prefilters for Descrete Multiwavelets Transforms,” IEEE Transactions on Signal Processing, Vol. 44, No. 1, 1996, pp. 25-35. doi:10.1109/78.482009
- E. Bala and A. Ertuzun, “A Multivariate Thresholding Technique for Image Denoising Using Multiwavelets,” EURASIP Journal on Applied Signal Processing, Hindawi Publishing Corporation, Cairo, 2005, pp. 1205-1211.
- T.-C. Hsung, D. P.-K. Lun and K. C. Ho, “Optimizing the Multiwavelet Shrinkage Denoising,” IEEE Transactions on Signal Processing, Vol. 53, No. 1, 2005, pp. 240-251.

