Journal of Signal and Information Processing
 Vol. 3  No. 2 (2012) , Article ID: 19554 , 7 pages DOI:10.4236/jsip.2012.32020

Self-Tuning Control for MIMO Network Systems*

Magdi S. Mahmoud, Matasm M. Hassan Hamid

Systems Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia.

Email: {msmahmoud, g200404060}@kfupm.edu.sa

Received October 19th, 2011; revised February 22nd, 2012; accepted March 20th, 2012

Keywords: MIMO Systems; Wireless Networks; Self-Tuning Control; Multi-Cast Networks

ABSTRACT

The advances in MIMO systems and networking technologies introduced a revolution in recent times, especially in wireless and wired multi-cast (multi-point-to-multi-point) transmission field. In this work, the distributed versions of self-tuning proportional integral plus derivative (SPID) controller and self-tuning proportional plus integral (SPI) controller are described. An explicit rate feedback mechanism is used to design a controller for regulating the source rates in wireless and wired multi-cast networks. The control parameters of the SPID and SPI controllers are determined to ensure the stability of the control loop. Simulations are carried out with wireless and wired multi-cast models, to evaluate the performance of the SPID and SPI controllers and the ensuing results show that SPID scheme yields better performance than SPI scheme; however, it requires more computing time and central processing unit (CPU) resources.

1. Introduction

The advances in multi-input multi-output (MIMO) systems and networking technologies introduced a revolution recently, which promises significant impact in our lives. Especially with ever-increasing multi-cast data applications, wireless and wired multi-cast (multipoint-to-multipoint) transmission has considerable effect on many applications such as teleconferencing and information dissemination services. Numerous research projects have been carried out to explore how to support multicast in various networking environments. Especially, these include systems that use multicast to deliver data and multimedia traffic [1]. Other systems support reliable and unreliable multicast over LANs [2], Internet [3], and networks including mobile hosts [4].

Multicast flow control is essential for high-performance multicast applications. Several techniques of flow control for atomic multicast protocols have been studied in [5] by simulations. A multicast flow control framework for combined wired/wireless networks has been proposed in [6]. In [6], Wang and Schwartz focused on the fundamental theory for controlling source rate, when source sends packets at a single rate. McCanne et al. in [7] proposed layered multicast to divide receivers into multiple subgroups. In layered multicast, several layers of information are provided and each receiver subscribes to one specific layer.

In explicit rate control, network devices in the path feed back multi-byte congestion information to end hosts so that the latter can timely and accurately adjust their congestion window sizes or sending rates in response to the current traffic situation in the network. An explicit rate control together with a simple window control has been proposed in [8] using for flow control in highspeed networks with resource reservations. An explicit rate control framework for Ethernet applications, especially data centers, has been described in [9]. Some related work and relevant applications are found in [10-15].

In this work, distributed design schemes of self-tuning proportional, integral plus derivative (SPID) controller and self-tuning proportional plus integral (SPI) controller are considered for multi-input multi-output network systems. For a brief account on self-tuning, the reader is referred to [16] and [17]. The control parameters are designed to ensure the stability of the control loop in terms of source rate. The control mechanism can be used to design a controller to support multipoint-to-multipoint multicast transmission based on explicit rate feedback. System stability criterion has been derived and analyzed.

The rest of this work is organized as follows. The network configuration system model is addressed in Section 2. In Section 3, SPID and SPI flow control algorithms are explained, while the stability of the system is analyzed in Section 4. Simulation results are obtained and discussed in Section 5. Finally, the conclusions are presented in Section 6.

2. Network Configuration Model

In our work, multicast configuration mode of multiple points to multiple points has been utilized, Figure 1. This

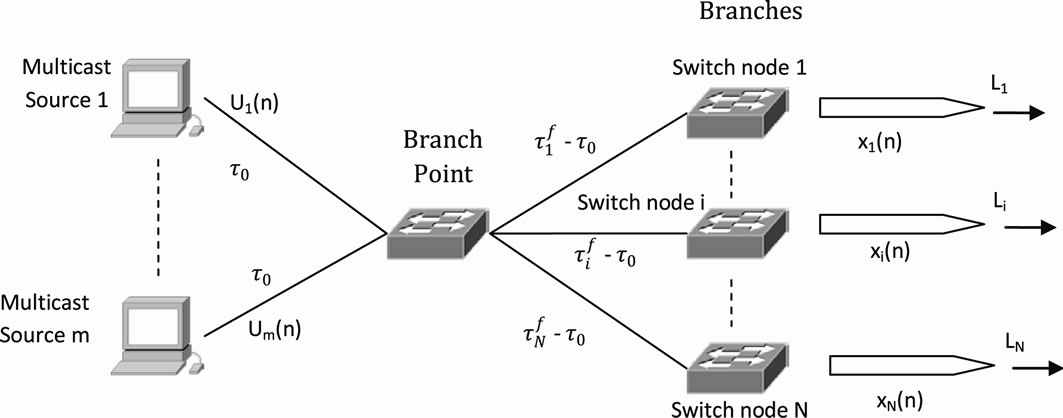
Figure 1. Multicast configuration mode of multiple points to multiple points.

multicast network is composed of sources and destination nodes. It is a connection-oriented one and time is slotted with the duration [n, n + 1] by the sampling period T. A fixed size packet has been transmitted between sources and destinations.

In each multicast connection and every sampling period, the multicast source issues and transmits a forward control packet (FCP) to the downstream nodes, which are the branch nodes and destination nodes, and a backward control packet (BCP) is constructed by each downstream node and sent back to the source. After the multicast source receives the BCPs from the downstream nodes, it will take appropriate action to adjust its transmitting rates of multicast traffic based on the computed value of the SPID controller. After receiving the data packets coming from the branch point, the receivers construct BCPs and send them back to the branch point.

The considered multicast service is described as follows. The number of packets sent out by the switch node i in one interval T is denoted by Li [18], the switch node i has the forward delay 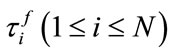from sources, and 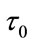is the delay from sources to the neighboring downstream node. Then, the round-trip delay (RTD) for the switch node i is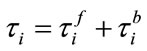, where, and =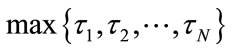. We further assume that 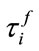and are integers, which is reasonable by adjusting T. And the link delay is dominant compared to the other delays, such as proceeding delay, queuing delay, etc. In the model, we assume that when. Each branch point schedules the packets in a first-come first-served way. The component 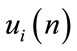represents the receiving rate of the computed receivers i at time slot n.

Based on the earlier considerations, the buffer occupancy of the switch node i after lifting the saturation restriction [10] is determined by [19].

(2.1)

where 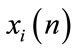is the buffer occupancy of the switch node i at time slot n, and 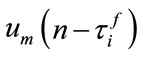is the sending rate of the source to the switch node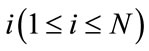, with

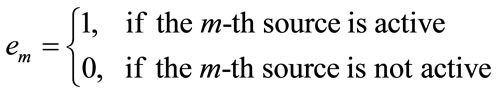
3. SPID and SPI Schemes

The router buffer occupancy is expected to stabilize in the neighborhood of the desired level. If 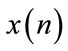is too low, it increases the likelihood of link under utilization during occasionally idle periods. Thus, the router buffer occupancy plays an important role in the congestion control that is chosen to be the feedback carried in BCP. If 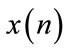is too high, it often leads to buffer overflow and packet loss. In addition, under this circumstance, long queuing delay usually results in time out and retransmission, which, in turn, builds up the mounting buffer occupancy; consequently, a vicious cycle is formed.

3.1. SPID and SPI Algorithms

Generally, among all downstream nodes, the most congested one, defined as the worst node, deserves special attention then SPID control scheme will be:

(3.1)

where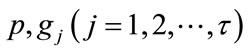, and r are the proportional, integral, and derivative control gains, respectively, which are to be determined by the stability criteria. These coefficients are used to locate all the poles of the closedloop Equations (2.1) and (3.1) within the unit circle to ensure stability. The component is the target queue length and is the maximum sending rate of sources. In order to save computing time and CPU resources, a simple SPI control scheme is presented as follows:

(3.2)

where 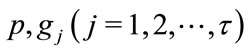are the proportional and integral control gains, respectively, which are to be determined from the stability criteria based on control theory. Similarly, these coefficients should make all the poles of the closed-loop Equations (2.1) and (3.2) within the unit circle to ensure stability. In (3.1) and (3.2), if the buffer occupancy of the switch node i is measured at the instances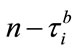, after the feedback delay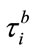, the BCP reaches the controller located at the source 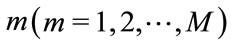, and the source then takes out the buffer occupancy of the destination nodes at time slot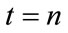. By doing so, the proposed controller can be expected to have flexibility to cope with the sharp oscillation in buffer occupancy that could cause the network to lose packets. In addition, the calculation in (3.1) and (3.2) is completely independent of virtual connections traveling through the multicast session. This means the scheme has scalability.

3.2. Implementation of SPID and SPI Algorithms

The branch point of the multicast tree replicates each data packet and FCP from its upstream node to all its downstream branches. The downstream nodes return their congestion information via BCPs to the parents through the backward direction of the coming path once they receive FCPs. Moreover, the branch nodes consolidate the BCPs that carry all the available rates and the relevant link bandwidth from different branches into one BCP and feedback the new BCP to their upstream node. Rate adapters associated are located at multicast source. There is a single FIFO (first-in-first-out) queue to multiplex all flows traveling through the outgoing link. Assume that congestion never happens at the router connected with the sources, hence these two can be consolidated into one node, which is true in most cases in real networks.

Before we present the algorithm in details, we specify the following variables. The variable multicast tree[i] = 1(0) means the ith branch point receive (do not receive) FCP or BCP control packet; while receiver tree[j] = 1(0) means the jth branch point receive (do not receive) confirmations of all destination nodes. Based on the above specifications, the pseudo-code of the proposed router and source algorithms in congestion control model of multiple points to multiple points in a multicast network is as follows.

• 3.2.1. Source Algorithm

• Upon every T epoch (say, time k): transmit data including FCP;

• Upon receipt of a consolidation BCP from its downstream: compute the sending rate based on consolidation BCP using SPID controller; adjust the transmitting rates based on computed sending rate.

• 3.2.2. Router Algorithm

• If 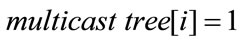if the packet is an FCP, put the data packet in the buffer; copy the data including FCP; multicast them to the downstream nodes; else construct the BCP based on the received BCPs; feedback it to the upstream node;

• If 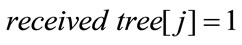delete the data packets from the buffer; else Maintain the data packets in the buffer until receive all confirmations of the receivers.

3.2.3. Destination Node Algorithm

Upon receipt of an FCP

• Put the data packets into the buffer;

• Construct the BCP based on the current congestion condition of the receiver nodes;

• Feedback the BCP to the upstream branch point.

4. System Stability Analysis

The ability of a multicast tree to provide efficient heterogeneous distributed communication that can guarantee multiple qualities of service can only be realized by effective traffic management schemes. In this work, a rate-based scheme is used rather than a window-based adaptation algorithm to achieve congestion control in multiratemulticast control (MR-MCC) tree. The windowbased scheme has extra complexity in maintaining and synchronizing the congestion window across all receivers, and it usually generates data bursts periodically [21]. In proposed SPID and SPI control schemes, the rate adaptation takes into account the buffer occupancies of the destination nodes as well as the variation of RTTs. The controller parameters are designed to guarantee the stability of rate, which ensures a smooth dynamic rate adaptation to minimize packet loss rate. This, in turn, brings an obvious advantage of the proposed scheme over the widely adopted additive increase and multiplicative decrease (AIMD) [21]. For example, in AIMD, it is difficult to choose the appropriate increase and decrease factors to guarantee the systems stability, and then to obtain smooth and healthy rate adaptation and good link utilization.

4.1. SPID System Stability Analysis

In this section, the stability of the proposed SPID congestion control scheme is analyzed as follows. Considering (2.1), if z transformation is applied, one can easily arrive at

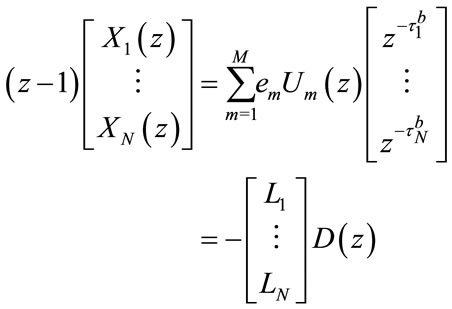(4.1)

where the z transformation of 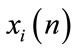and are, respectively, described by

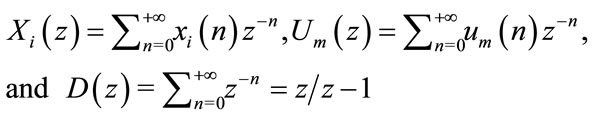
Taking the z-transform of Equation (3.1), one yields:

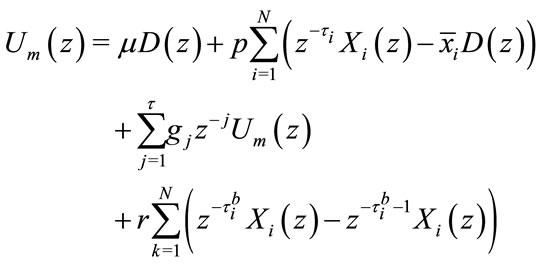(4.2)

from (4.1) and (4.2) we have

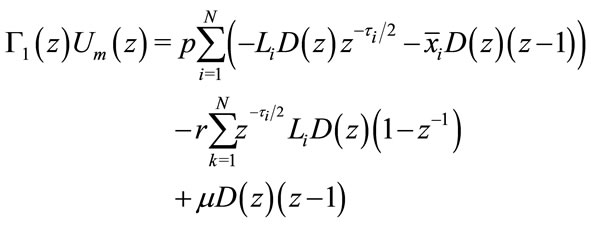(4.3)

where

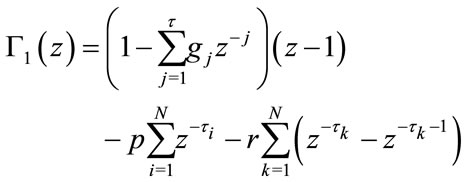(4.4)

After algebraic simplifications, it can be written as

(4.5)

The coefficients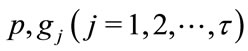, and r are determined by the stability criteria of the control theory. The component is the characteristic polynomial (CP) of the multicast system given by (2.1) and (3.1) [18]. The CP (4.4) is closely related to the stability of the congestion-controlled network system. From a controltheoretic view, when all the zeros of (4.4) lie within the unit disc, the original network system (2.1) with the controller (3.1) is stable in terms of the source sending rates. Stability is a prerequisite in congestion control to ensure that the network has no oscillation of sending rate, and thus minimizes the packet loss rate. For this reason, Routh-Hurwitz criterion [22] has been used for testing stability. Then, a bilinear transformation has been utilized to transform the unit circle of the z-plane into the imaginary axis of the w-plane by 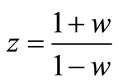then (4.5)

can be written as

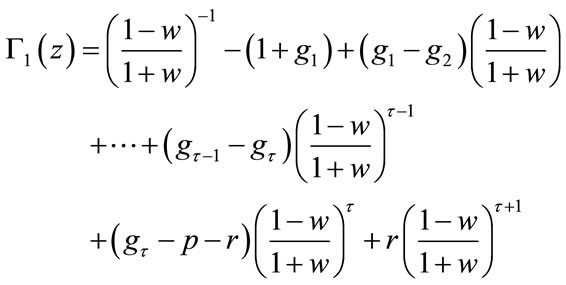
After clearing the fraction by multiplying both side of (4.6) by 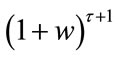and.

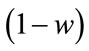(4.6)

where. Therefore the stability of system may be determined by directly applying the Routh-Hurwitz criterion [23].

4.2. SPI System Stability Analysis

The stability of the proposed SPI congestion control scheme is analyzed same as SPID method. Taking the ztransform of Equation (3.2), one yields:

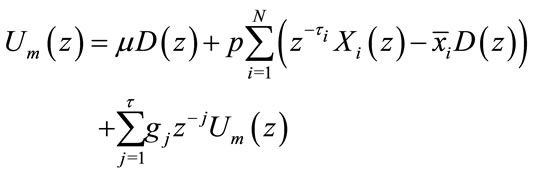(4.7)

From (4.1) and (4.7) we have 

(4.8)

where

(4.9)

The coefficients p and 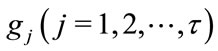are determined by the stability criteria of the control theory. Then after using bilinear transformation (4.6) can be written as

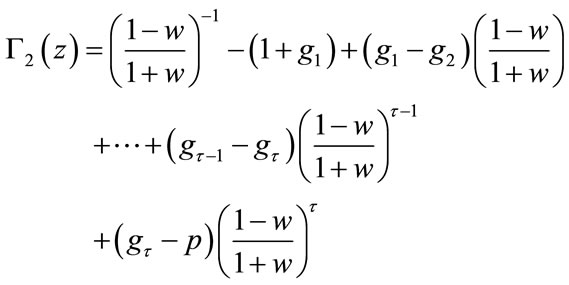(4.10)

After multiplying both side of (4.10) by and.

(4.11)

where. Therefore the stability of system may be determined by applying the Routh-Hurwitz criterion.

5. Simulation Results

To evaluate the performance of the studied multicast congestion control scheme, we focus on the following two simulation models, and are mostly interested in analyzing the transient behaviors of the network. In the performance analysis, the duration of response time, receiving rate of receivers, and steady state of buffer occupancy are the main concerns.

From control theory viewpoint, a control scheme with short response time has the following advantages: when the buffer of receiver nodes is close to the threshold, one may tell the sending node to reduce the sending rate and prevent the loss of packets as soon as possible; while when the available bandwidth increases, the sending node increases the sending rate as soon as possible and enhances the utilization rate of the bandwidth. In simulations, we process the nodes that have small differences of time delay and sending rate together. Then we unify the time delay and sending rate. Since the situation of every node in each group (about 20 receivers) is similar, we only choose one node from each group as a representative. We assume that the link delay is dominant compared to the other delays, such as processing delays and queuing delay.

Simulations are carried out over a wide range of patterns, and propagation between two different nodes can lie in the LAN case or the WAN case. Multicast system model for our simulation has been shown in Figure 2. The multicast source S1 sends data packets at 0 ms and the multicast source S2 starts to send data packets at 1000 ms in the simulation time; then the joining of S2 enhances the network dynamic behavior, and also demonstrates the efficiency of the SPID and SPI schemes.

Figure 2. Multicast system model.

In this simulation, we focus on comparing the transient behavior of the SPID and SPI network systems based on Figure 2. The relevant notations and assumptions are listed in Table 1, and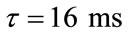, N = 60 and n1 = n2 = n3 = 20. According to the aforementioned simulation parameters and system stability analysis in Section 4 to select the control gains.

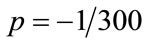For SPID scheme, which is stable in the system. Then, and, i.e., q = [–19/20, –9/10, –17/20, –8/10, –2/3, –2/3, –37/60, –34/60, –26/60, –26/60, –23/60, –20/60, –17/60, –14/60, –11/60, –7/60, –4/60]. For SPI scheme, which is stable in the system. Then, and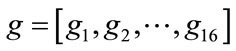, i.e., g = [–19/20, –9/10, –17/20, –41/60, –38/60, –37/60, –35/60, –32/60, –25/60, –23/60, –28/60, –15/60, –12/60, –10/60, –7/60, –5/60].

In this section, the simulation results have been shown in Figures 3-5. Figures 2 and 4 the sending rates of sources S1 and S2 have been shown , respectively. The initial sending rate of multicast source S1 is 6 Mb/s. It can be seen that, although the sending rate of the multicast source S1 has some fluctuation at first, as time goes on, the sending rate is gradually adjusted and quickly at the value of 2 Mb/s within 120 ms for SPID controller, and 160 ms for SPI controller. When the multicast source S2 starts to send data packets at 1000 ms, the sending rate of source S1 has some fluctuation in response to the multicast source S2 joining, and quickly stabilizes at the new value of 1 Mb/s within 130 ms for SPID controller and 170 ms for SPI controller. The buffer transient responses of the receiver node 21 has been shown in Figure 4. This buffer occupancies of the bottleneck receivers all have some fluctuation in the beginning. Then they gradually become stable at the value 37 Mb for SPID controller and 127 Mb for SPI controller. When the multicast source S2 starts to send data packets at 1000 ms, the buffer occupancies of the receivers have some fluctuation in response to the multicast source S2 joining. For receiver group 2, they quickly become stable at the value 155 Mb for SPID controller and 173 Mb for SPI controller.

Table 1. Parameters for simulation model.

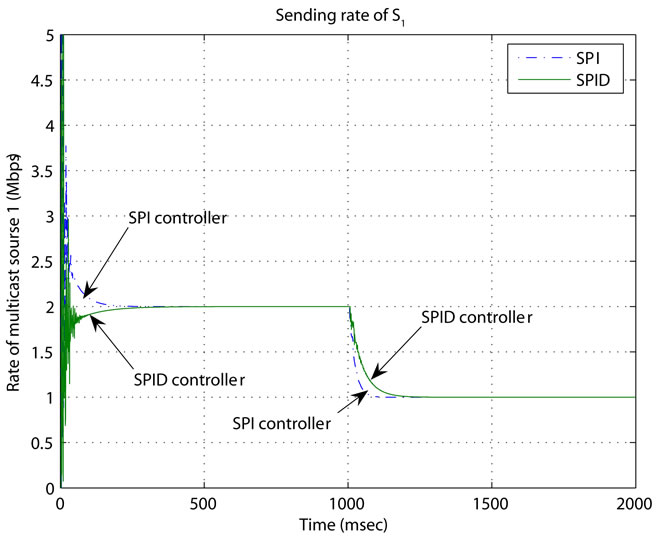
Figure 3. The sending rate of multicast source S1.

Figure 4. The sending rate of multicast source S2.

From these simulation results we observe that two schemes could quickly adjust the buffer occupancy and the rates of sending node based on the dynamic network environment. These simulation results demonstrate our SPID and SPI controllers, efficiency in terms of system stability, fast response, low packet loss, and high scalability. Based on our schemes, the source adjusts the sending rate gradually to stabilize the buffer occupancy and rate of sending node quickly. In terms of the fast response of the controlled sending rates and low buffer occupancy of bottleneck receivers, SPID controllers can provide better performance than SPI controllers.

Figure 5. The transient response of buffer occupancy in receiver node 21.

6. Conclusion

In this work, SPID and SPI schemes have been presented, using an explicit rate feedback mechanism to design a controller for regulating the source rates in wireless and wired multi-point-to-multi-point multi-cast networks. Depending on the network load, the control parameters of the SPID and SPI controllers can be determined to ensure the stability of the control loop in terms of buffer occupancy and adjust automatically. This subsequently means that the schemes provide the least packet loss in steady state. To evaluate the performance of the SPID and SPI controllers, Simulations have been carried out with wireless and wired multi-point-to-multi-point multicast models. The simulation results clearly demonstrate the efficiency of our scheme in terms of system stability and fast response of the buffer occupancy, as well as controlled sending rates, low packet loss, and high scalability. The simulation results also show that SPID scheme has better performance than SPI scheme; however, SPID scheme requires more computing time and CPU resources.

REFERENCES

  1. Y. Amir, D. Dolev, S. Kramer and D. Malki, “Transis: A Communication Sub-System for High Availability,” TwentySecond International Symposium on Fault-Tolerant Computing, 8-10 July 1992, pp. 76-84.
  2. A. P. Naryan, “Reliable Transfer of Data in a Local Area Network with Multicast Distribution,” 15th Conference on Local Computer Networks, McLean, 30 September-3 October 1990, pp. 310-319.
  3. S. Floyd, V. Jacobson, C.-G. Liu, S. McCanne and L. Zhang, “A Reliable Multicast Framework for Light-Weight Sessions and Application Level Framing,” 15th Conference on Local Computer Networks, McLean, Vol. 5, 1997, pp. 784-803.
  4. M. Gerla, C.-C. Chiang and L. Zhang, “Tree Multicast Strategies in Mobile, Multihop Wireless Networks,” Mobile Networks and Applications, Vol. 4, No. 3, 1999, pp. 193-207. doi:10.1023/A:1019150932356
  5. S. Mishra and L. Wu, “An Evaluation of Flow Control in Group Communication,” IEEE/ACM Transactions on Networking, Vol. 6, No. 5, 1998, pp. 571-587. doi:10.1109/90.731193
  6. H. Wang and M. Schwartz, “Performance Analysis of Multicast Flow Control Algorithms over Combined Wired/ Wireless Networks,” IEEE Journal of Selected Areas in Communications, Vol. 15, No. 7, 1997, pp. 1349-1363. doi:10.1109/49.622917
  7. S. McCanne, V. Jacobson and M. Vetterli, “ReceiverDriven Layered Multicast,” Conference Proceedings on Applications, Technologies, Architectures, and Protocols for Computer Communications, Vol. 26, No. 4, 1996. doi:10.1145/248156.248168
  8. F. Gong and G. Parulkar, “Study of a Two-Level Flow Control Scheme and Buffering Strategies,” INFOCOM’94. Networking for Global Communications, 13th Proceedings IEEE, Vol. 3, 1994, pp. 1224-1233.
  9. J. Jiang, R. Jain and C. So-In, “An Explicit Rate Control Framework for Lossless Ethernet Operation,” Proceedings of IEEE International Conference on Communications, Beijing, May 2008, pp. 19-23.
  10. X. Zhang and K. G. Shin, “Statistical Analysis of Feedback Synchronization Signaling Delay for Multicast Flow Control,” IEEE/ACM Transactions on Networking, Vol. 11, No. 3, 2003, pp. 436-450. doi:10.1109/TNET.2003.813035
  11. Y. Z. Cho, S. M. Lee and M. Y. Lee, “An Efficient Rate-Based Algorithm for Point-to-Multipoint ABR Service,” Global Telecommunications Conference, 3-8 November 1997, Vol. 2, pp. 790-795.
  12. X. Zhang, K. G. Shin, D. Saha and D. D. Kandlur, “Scalable Flow Control for Multicast ABR Services in ATM Networks,” IEEE/ACM Transactions on Networking, Vol. 10, No. 1, 2002, pp. 67-85. doi:10.1109/90.986538
  13. A. Kolarov and G. Ramamurthy, “A Control Theoretic Approach to the Design of an Explicit Rate Controller for ABR Service,” IEEE/ACM Transactions on Networking, Vol. 7, No. 5, 1999, pp. 741-753. doi:10.1109/90.803387
  14. F. Blanchini, R. L. Cigno, and R. Tempo, “Robust Rate Control for Integrated Services Packet Networks,” IEEE/ ACM Transactions on Networking, Vol. 10, No. 5, 2002, pp. 644-652. doi:10.1109/TNET.2002.803896
  15. S. H. Lee and J. T. Lim, “Multicast ABR Service in ATM Networks Using a Fuzzy-Logic-Based Consolidation Algorithm,” Proceedings of Industrial Electronic Engineering Communications, Vol. 148, No. 1, 2001, pp. 8-13.
  16. K. L. Chien, J. A. Hrons and J. B. Reswick, “On the Automatic Control of Generalized Passive Systems,” Transactions of the American Society of Mechanical Engineeing, Vol. 74, 1972, pp. 175-185.
  17. P. E. Wellstead and M. B. Zarrop, “Self-Tuning Systems,” John Wiley & Sons Ltd., New York, 1991.
  18. L. Rizzo, “Pgmcc: ATCP-Friendly Single-Rate Multi- cast Congestion Control Scheme,” Proceeding of the ACM SIGCOMM, Stockholm, 2000, pp. 17-28.
  19. N. Xiong, Y. He and Y. Yang, “An Efficient Flow Control Algorithm for Multi-Rate Multicast Networks,” 2004 IEEE Workshop on IP Operations and Management Proceedings, Beijing, 11-13 October 2004, pp. 69-76.
  20. L. Lao, J. H. Cui, M. Gerla and D. Maggiorini, “A Comparative Study of Multicast Protocols: Top, Bottom, or in the Middle,” IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies, Barcelona, 23-29 April 2006.
  21. S. Ratnasamy, A. Ermolinskiy and S. Shenker, “Revisiting IP Multicast,” Proceeding of the ACM SIGCOMM, Pisa, 11-15 September 2006, pp. 15-26.
  22. A. Hurwitz, “On the Conditions under Which an Equation Has Only Roots with Negative Real Parts,” Mathematische Annelen, Vol. 46, 1985, pp. 273-284.
  23. K. Ogata, “Discrete-Time Control Systems,” 2nd Edition, Prentice-Hall, Inc., New York, 1995.

NOTES

*This work is supported by the deanship for scientific research (DSR) at KFUPM through research group project RG1105-1.

Journal Menu >>