Journal of Software Engineering and Applications
Vol.5 No.7(2012), Article ID:19727,5 pages DOI:10.4236/jsea.2012.57053
A Retrieval Matching Method Based Case Learning for 3D Model*
![]()
College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou, China.
Email: lzhi@zjut.edu.cn
Received March 1st, 2012; revised April 6th, 2012; accepted April 19th, 2012
Keywords: case learning-based; retrieval matching; similarity matching
ABSTRACT
The similarity metric in traditional content based 3D model retrieval method mainly refers the distance metric algorithm used in 2D image retrieval. But this method will limit the matching breadth. This paper proposes a new retrieval matching method based on case learning to enlarge the retrieval matching scope. In this method, the shortest path in Graph theory is used to analyze the similarity how the nodes on the path between query model and matched model effect. Then, the label propagation method and k nearest-neighbor method based on case learning is studied and used to improve the retrieval efficiency based on the existing feature extraction.
1. Introduction
Recent technological developments have made 3D acquisition, modeling, and visualization technologies widely accessible to various domains including CAD, entertainment, and virtual reality. All these applications will use large-scale collections of 3D models and how to extract and reuse these 3D efficiently becomes a key issue [1-3]. Nowadays many 3D retrieval tools are studied for browsing the large collections.
In general, 3D retrieval system is composed of two parts. One part is to extract the model feature. How to select the good model feature and maximize the model information will be beneficial to improving the retrieval rate. Another part is to match the model similarity. Based on the extracted model feature, some ways will be selected to compare the similarity between the models. In the feature extraction, there are two kinds of methods including content-based feature extraction and semantic-based feature extraction. For the model similarity matching methods, there are mainly two kinds of methods: based on geometric distance and based on nongeometric distance [4]. These methods are also based on the feature extraction. Only good feature extraction method coupling with the similarity matching method together can achieve a good retrieval rate.
Now the existing similarity matching methods in3D model retrieval systems have reached rather good retrieval results, but most of these systems only use the single method. The model features extracted in this way will be not highly robust and very sensitive to noise. It will result in unsatisfactory search results. Therefore there is an urgent need to study a better way to break through similarity matching limitation based on the traditional single method. In this paper, the label propagation method is used in the similarity matching based on feature extraction and the single source shortest path method and K-nearest neighbor learning method are combined to form a new method for similarity matching. Since this method increases the breadth of match to a certain extent, it improves the 3D model retrieval efficiency.
2. Related Works
2.1. Single-Source Shortest Path
Single-source shortest path [5] describes the problem how to find the shortest distance to other vertices from the certain source vertex in a graph. The connections between the vertex and all other vertices on the path from the starting vertex to the target vertex will affect the distance between these two vertices. When there are multiple pathways between the source vertex and target vertex, the shortest distance between them is regarded as the shortest path.
This thinking can be used in similarity matching of 3D model retrieval. The shortest path method can be used to expand the breadth of geometric distance metric in the 3D similarity matching method based on geometric distance. Here, the similarity matching no longer depends on one geometric distance measure result, but on the minimum value among the multi geometric distance metric results. It will improve the retrieval rate to some extent.
Assuming that there are model  in the collections of 3D models and the distance metric function d in the similarity matching method based on geometric distance, then there is an inequality:
in the collections of 3D models and the distance metric function d in the similarity matching method based on geometric distance, then there is an inequality:  . Introducing the thinking of single-source shortest path in the similarity matching method, we can find a new distance metric function d'. There will be an inequality:
. Introducing the thinking of single-source shortest path in the similarity matching method, we can find a new distance metric function d'. There will be an inequality: 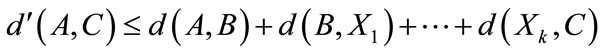 . So it will improve the previous matching results.
. So it will improve the previous matching results.
2.2. Label Propagation
In the webpage search method, a kind of correlation matching method is often used. The retrieved webpage depends on correlation between the keywords in the webpage and the given keywords. When a webpage has a strong correlation with the webpage that matches the retrieval condition best, the webpage will be regarded as retrieval result. So a lot of matching webpage will be found. In view of this idea, we use the label propagation to the similarity matching of 3D model.
Label propagation [6-8] is a kind of semi-supervised learning method. It is assumed that the classification label is known for small quantities in a data set, then a propagation algorithm is used to push out the labels to the unlabeled data in the rest of the data set. In the similarity matching of 3D model retrieval, it is assumed that only the label of query model is known. The label propagation method is based on graph structure. Whether the label of a node can propagate to the neighbor node or not is determined by the similarity between them.
Here, we assume that the labeled data set is 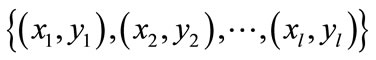 , in which
, in which  is a classification label. The C is known and is defined as the total number of categories. The x is the data in the data set.
is a classification label. The C is known and is defined as the total number of categories. The x is the data in the data set. 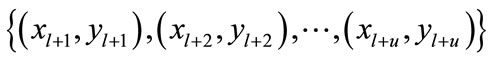 is unlabeled data set, in which
is unlabeled data set, in which . The whole data set is
. The whole data set is . In label propagation method, the unlabeled data
. In label propagation method, the unlabeled data 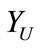 will be mapped to set
will be mapped to set 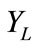 through label propagation algorithm. Usually, the l is much smaller than u.
through label propagation algorithm. Usually, the l is much smaller than u.
Each data in the data set X is taken as a node and weighted graph is constructed. The weight value  connecting
connecting 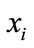 and
and  can be calculated in several methods. Here, we use the simple Euclidean distance to calculate the weight. The
can be calculated in several methods. Here, we use the simple Euclidean distance to calculate the weight. The 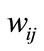 is inversely proportional to its Euclidean distance between them. The greater the distance, the less the similarity. It will also be affected by the parameters. The formula of
is inversely proportional to its Euclidean distance between them. The greater the distance, the less the similarity. It will also be affected by the parameters. The formula of 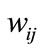 is
is
 . The labels are propagated through the edges connecting with the nodes. The greater the weight on the edge connecting with two nodes is, the easier the label is propagated. The total number of nodes
. The labels are propagated through the edges connecting with the nodes. The greater the weight on the edge connecting with two nodes is, the easier the label is propagated. The total number of nodes 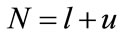 is known. Constructing a matrix
is known. Constructing a matrix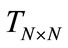 , in which
, in which
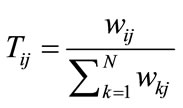 represents the probability of propagation from node
represents the probability of propagation from node  to node
to node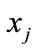 .
.
Constructing a matrix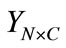 , in which
, in which  represents the probability that node
represents the probability that node  is belong to the classification of
is belong to the classification of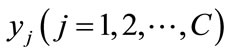 . The classification label is propagated as below:
. The classification label is propagated as below:
1) The node classification is propagated to neighboring nodes according to a certain probability;
2) The data in the matrix Y from the line 1 to line l will be reverted to the initial value and the data in the rest lines will be normalized;
3) Repeating the above steps until the Y is converged.
2.3. Case-Based K-Nearest Neighbor Learning Method
Case-based Reasoning (CBR) has become a very popular AI technique [9,10]. It is based on the assumption that problems can be solved efficiently by reusing knowledge about similar, already solved problems stored in the collections of cases. The case-based learning is also called passive learning. Because the training cases are simply stored in memory without any evaluation or classification, they will be treated only when a new case comes. An important advance in this passive learning method is that it is not one-time estimated objective function on the whole instances space, but on local space and using different estimation for each new instance.
The case-based K-nearest neighbor method assumes that all cases X corresponds to the points in n-dimensional space . The distance between case
. The distance between case 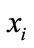 and case
and case 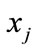 is defined as
is defined as
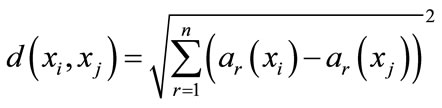 . The value of target function
. The value of target function 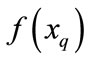 can be a discrete value or can also be real. For the distance-weighted K nearest neighbor method, the inverse of square of distance between each neighbor
can be a discrete value or can also be real. For the distance-weighted K nearest neighbor method, the inverse of square of distance between each neighbor 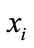 and the query node
and the query node 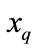 the is used to calculate the weight
the is used to calculate the weight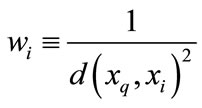 . If the query node coincides with the training case
. If the query node coincides with the training case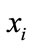 , the denominator
, the denominator 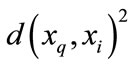 will be 0. So under this situation, we define
will be 0. So under this situation, we define
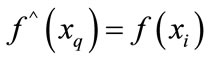 .
.
Here,  is the classification for the training cases. The target function is f and the query case is V. The learning process is below:
is the classification for the training cases. The target function is f and the query case is V. The learning process is below:
1) Firstly, each training case 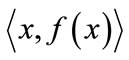 will be added into training_examples;
will be added into training_examples;
2) Input a query case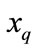 , select k cases that are nearest to
, select k cases that are nearest to 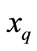 in the training_examples and represent them with
in the training_examples and represent them with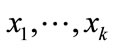 ;
;
3) Calculate  and return.
and return.
3. Learning Based Retrieval
3.1. Background
In 3D model retrieval system, only a good feature extraction method is not enough. It there is no good method for similarity matching, the retrieval results will not be good. Here, the learning-based dissimilarity calculation is proposed to reduce the error similarity matching. It will improve the search accuracy.
In general model retrieval method, when the query model  is compared to model
is compared to model 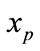 with similarity, the neighbor models of
with similarity, the neighbor models of 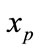 will not be considered. In fact, in the learning-based dissimilarity calculation method, when model a is more similar with model b, the model a is more similar with the neighbor models of model b. This is consistent with the facts and it can improve the retrieval accuracy and recall rate. The existing dissimilarity calculation does not reflect this characteristic [11].
will not be considered. In fact, in the learning-based dissimilarity calculation method, when model a is more similar with model b, the model a is more similar with the neighbor models of model b. This is consistent with the facts and it can improve the retrieval accuracy and recall rate. The existing dissimilarity calculation does not reflect this characteristic [11].
In this paper, the new learning-based dissimilarity calculation method not only takes into the individual characteristics of compared model, but also considers the characteristics of its nearest neighbor model. Here, the single-source shortest path, label propagation, and casebased K-nearest neighbor learning method are combined together in order to improve the retrieval accuracy and recall rate.
3.2. Learning-Based Dissimilarity Calculation
Assume that the original target function of dissimilarity calculation is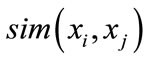 , the value of this function is the value of Gaussian density function of distance
, the value of this function is the value of Gaussian density function of distance
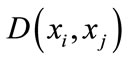 between the node
between the node . Here, weight value is defined as
. Here, weight value is defined as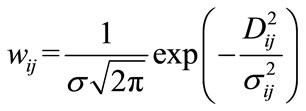 . The smaller the value is, the more similar the nodes are. In the learningbased dissimilarity calculation, a new function
. The smaller the value is, the more similar the nodes are. In the learningbased dissimilarity calculation, a new function 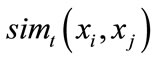 is introduced as the dissimilarity between the model
is introduced as the dissimilarity between the model  and query model
and query model . The subscript t represents the number of iterations.
. The subscript t represents the number of iterations.
When the iteration is terminated, the t is up to T and 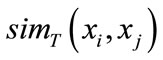 will be the value of dissimilarity between the model
will be the value of dissimilarity between the model  and query model
and query model . The function
. The function  is the improved function of the existing similarity metric function
is the improved function of the existing similarity metric function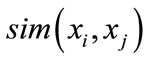 . It is combined the learning-based dissimilarity calculation, shortest-path, and label propagation.
. It is combined the learning-based dissimilarity calculation, shortest-path, and label propagation.
In the existing dissimilarity calculation method,
 , in which
, in which
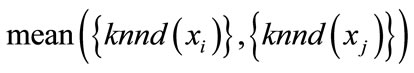 is the mean distance of k nearest neighbor between model
is the mean distance of k nearest neighbor between model 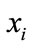 and model
and model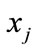 . The k and
. The k and 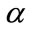 are determined by experiments [11]. For matrix W, a new matrix P is introduced and improves the weight calculation. Here,
are determined by experiments [11]. For matrix W, a new matrix P is introduced and improves the weight calculation. Here, 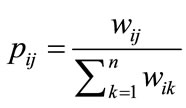 , it represents the probability of similarity between model
, it represents the probability of similarity between model  and model
and model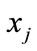 . This comes from the thinking of label propagation. When a model
. This comes from the thinking of label propagation. When a model 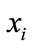 has very high similarity with many models in the collection of model, the
has very high similarity with many models in the collection of model, the 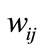 is smaller and
is smaller and 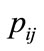 is bigger. That means the model
is bigger. That means the model 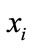 has strong correlation with other models and it has a greater probability to be retrieved.
has strong correlation with other models and it has a greater probability to be retrieved.
In the case-based K nearest neighbor method, the key function 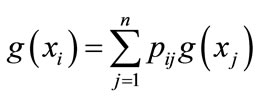 is introduced. It represents the value of dissimilarity between model
is introduced. It represents the value of dissimilarity between model  and model
and model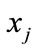 . Here, assume
. Here, assume , in which model
, in which model  is the query model and model
is the query model and model 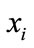 is the training model in the collection of models. The solution of this iteration function is below:
is the training model in the collection of models. The solution of this iteration function is below:
1) Initialize ,
, 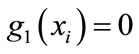 , i = 2, ∙∙∙, n;
, i = 2, ∙∙∙, n;
2) Iteration process: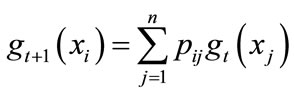 , i = 2, ∙∙∙n and
, i = 2, ∙∙∙n and ;
;
3) The terminal condition is when the 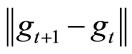 tends to infinitesimal. Then setting a threshold, when t is up to T, the calculation result of
tends to infinitesimal. Then setting a threshold, when t is up to T, the calculation result of  is the finial result.
is the finial result.
After finishing the calculation of matrix W, the matrix P can be calculated as above. When the 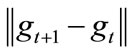 satisfies the threshold condition, the iteration process stops [12].
satisfies the threshold condition, the iteration process stops [12].
When this iteration is over, the dissimilarity of model  and model
and model  can be calculated as
can be calculated as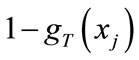 . Then the values of dissimilarity are sorted in ascending order. The smaller the value, the more similar the models.
. Then the values of dissimilarity are sorted in ascending order. The smaller the value, the more similar the models.
4. Experiment Results
In this experiment, the test database is PSB that is provided by Princeton University. The result is tested by the test function provided by Princeton University [13]. The original Euclidean distance-based similarity matching method is tested as Figure 1.
In the spherical harmonics based feature extraction, the test result of the new learning-based similarity matching is Figure 2.
The two results are put into a same graph and are compared as Figure 3.
Experimental results show that the learning-based retrieval method improves the existing retrieval rate of geometric distance-based similarity matching method in certain extent. The disadvantage of this method is that the retrieval rate is impacted by the result of feature extraction. The size of collection of 3D models will also impact the choice of K value. If the extracted features can not represent the original model well, the retrieval rate
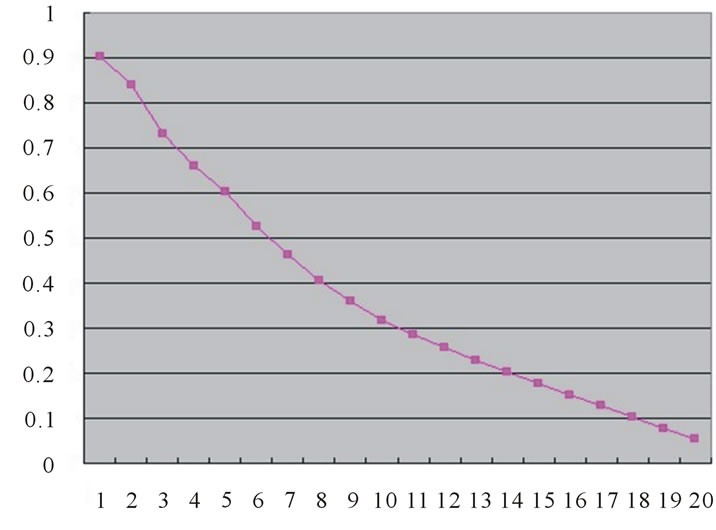
Figure 1. Result of Euclidean distance-based similarity matching method.

Figure 2. Result of learning-based similarity matching method.
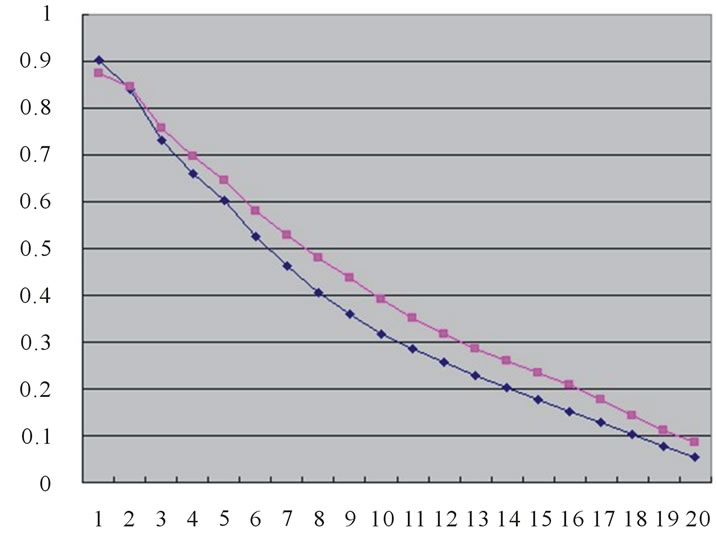
Figure 3. The comparison of tow test results.
will be significantly affected.
5. Conclusions
The traditional distance metric-based similarity matching method limits the breadth of model matching. It makes the search results can not very well reflect the similarity between models. This paper proposed and implemented a case learning-based similarity matching method. It expands the breadth of model matching and provides more detailed classification and more accurate matching basis during the model classification process.
This method combines the shortest path, label propagation and case-based K-nearest neighbor learning method based on the existing feature extraction. It improves the existing retrieval rate of geometric distance-based similarity matching method in certain extent.
In the further work, some different learning methods could be taken into count in order to expand the breadth of model matching and improve the retrieval rate.
REFERENCES
- Y. B. Yang, J. Lin and Q. Zhu, “Content-Based 3D Model Retrieval: A Survey,” Chinese Journal of Computers, Vol. 27, No. 10, 2004, pp. 1297-1310.
- B. C. Zheng, W. Peng, Y. Zhang, X. Z. Ye and S. Y. Zhang, “A Survey on 3D Model Retrieval Techniques,” Journal of Computer-Aided Design & Computer Graphics, No. 7, 2004.
- X. Pan, “Analysis and Retrieval of 3D Model Retrieval shape,” Zhejiang University, Hangzhou, 2005.
- C. Y. Cui, “Research on the Key Technology of 3D Model Retrieval,” Zhejiang University, Hangzhou, 2005.
- F. Lu, “Shortest Path Algorithms: Taxonomy and Advance in Research,” Acta Geodaeticaet Cartographica Sinica, No. 03, 2001.
- M. Wu and R. Jin, “Label Propagation for Classification and Ranking,” Michigan State University, Lansing, 2007.
- X. J. Zhu and Z. B. Ghahramani, “Learning from Labeled and Unlabeled Data with Label Propagation. Technical Report CMU-CALD-02-107,” Carnegie Mellon University, Pittsburgh, 2002.
- J. Chen, Y. Zhou, B. Wang, L. B. Luo and W. Y. Liu, “Rapid Shape Retrieval Using Improved Graph Transduction,” IEEE Conferences on Information Engineering and Computer Science, Wuhan, 19-20 December 2009, pp. 1-4. doi:10.1109/ICIECS.2009.5366255
- T. M. Mitchell, “Machine Learning: Case-Based Learning,” McGraw Hill, New York, 1997.
- W. W. Lu and J. Liu, “New Algorithm to Scale up Efficiency of K-Nearest-Neighbor,” Computer Engineering and Applications, No. 4, 2008.
- X. Yang, X. Bai, L. J. Latecki and Z. Tu, “Improving Shape Retrieval by Learning Graph Transduction,” ECCV, 2008.
- X. Bai, X. W. Yang, L. J. Latecki, W. Y. Liu and Z. w. Tu, “Learning Context-Sensitive Shape Similarity by Graph Transduction,” PAMI.2009.85, 2010, pp. 861-874.
- Princeton Shape Retrieval and Analysis Group, 2012. http://www.cs.princeton.edu/gfx/proj/shape/
NOTES
*This research work is supported by Zhejiang Province Science and Technology Agency Project. The Project No. is 2009C11038.

