Agricultural Sciences
Vol.06 No.10(2015), Article ID:60292,15 pages
10.4236/as.2015.610110
Response of Two Inexpensive Commercially Produced Soil Moisture Sensors to Changes in Water Content and Soil Texture
Tyson B. Raper1*, Christopher G. Henry2, Leo Espinoza3, Mukhammadzakhrab Ismanov3, Derrick M. Oosterhuis4
1Department of Plant Sciences, University of Tennessee, Jackson, TN, USA
2Department of Biological and Agricultural Engineering, University of Arkansas, Stuttgart, AR, USA
3Department of Crop, Soil and Environmental Sciences, University of Arkansas, Little Rock, AR, USA
4Department of Crop, Soil and Environmental Sciences, University of Arkansas, Fayetteville, AR, USA
Email: *traper@utk.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 April 2015; accepted 12 October 2015; published 15 October 2015
ABSTRACT
The use of low-cost (<200 USD) soil moisture sensors in crop production systems has the potential to give inference on plant water status and therein drive irrigation events. However, commercially available sensors in this price range vary in sensing methodologies and limited information on sensor to sensor relationship is available. The objective of this research was to test the response of the Watermark 200SS and Decagon 10HS sensors to changes in water content of three dissimilar soils representing common soils in Arkansas row-crop production in nine plastic, 19 L containers under variable environmental conditions. Both sensors were influenced by changes in soil temperature but the magnitudes of the temperature responses were small relative to the moisture responses. Furthermore, the 10HS sensor did not indicate a significant impact of soil texture on estimated volumetric water contents (VWCs). The small sphere of influence on the tested soil moisture parameters coupled with the substantial evaporative demands and temperatures under which this experiment was conducted resulted in suspected non-uniform drying and wetting of the tested containers. Subsequently, non-linear relationships were noted between 10HS estimated VWCs and actual container VWCs and the 200SS predicted lower water potentials than calculated by converting container VWC to soil water potential. The failure of the sensors to accurately predict container VWC highlights the importance of understanding the relatively small quantity of soil on which these sensors rely as well as the potential variability in soil moisture within a very limited volume. The authors caution users of sensors that soil variability may be one of the most important considerations in sensor deployment.
Keywords:
Soil Moisture, Sensor, 10HS, Watermark, 200SS, Decagon, Comparison, Soil Texture

1. Introduction
The most critical step in irrigation scheduling is the determination of plant available water (PAW) relative to a yield-reducing lower water limit. In the humid Mid-South and Southeastern regions of the USA, this step has traditionally consisted of an indirect inference on water status through a visual inspection of the crop or soil. Historically water balance or “checkbook” methods have been the irrigation scheduling tools used in the region. The primary deficiency in these methods is that they rely on estimated volumes of daily crop water use instead of experimentally verified volumes [1] so if they are not well calibrated to a particular region or field situation they can over or underestimate irrigation needs. Another assumption that computer-based schedulers make is irrigation efficiency, which can lead to errors in the water balance. Additionally, with in-furrow irrigation applications, the profile is often assumed to be refilled and this may not be a valid assumption. This can lead to the accumulation of large errors in the water balance by season end. The characterization of in-field soil moisture conditions through some real-time measurement has the potential to give producers insight into actual crop water status and remove many uncertainties associated with more arbitrary methods of irrigation scheduling. Such tools also allow for the calibration and validation of assumptions made with computerized based schedulers.
Recent advancements in electronics have resulted in a dramatic increase in the number of commercially available soil moisture sensors, many of which vary substantially in cost and application [2] - [4] . Still, only a few of these sensors are inexpensive enough to be appropriate for large deployments necessary for spatially dense readings. Two sensor types which currently meet these criteria are soil granular matrix potential sensors and low-frequency, capacitance-based sensors. Granular soil matrix potential sensors have been commercially available for many years and use resistance between two electrodes to infer soil water potential. Low-frequency, capacitance-based sensors have been commercially introduced more recently. In contrast to the granular matrix, tensiometric sensors, the low-frequency, capacitance based sensors rely on the dielectric characteristics of the sensing medium to infer volumetric water content (VWC).
1.1. Tensiometric Sensors
Sensors estimating soil matric potential include tensiometers, gypsum blocks, granular matrix sensors, heat dissipation sensors, and soil psychrometers [3] . The majority of these sensors estimate the amount of energy (potential) with which soil water is held by monitoring water movement through a porous material in contact with the soil. Granular matrix sensors are widely used for large deployments due to their low cost. These sensors are typically composed of two electrodes embedded into a cylindrical granular matrix which is buried in the soil. The granular matrix equilibrates to soil water content by the transfer of water from the surrounding soil. Soil water potential is thereby related to the change in resistance between the two embedded electrodes. Specifically, a decrease in resistance is associated with an increase in soil matric potential. This matric potential can be translated to volumetric water content by developing a water retention relationship experimentally. One of the most commonly used granular matrix sensors is the Watermark Model 200SS (Irrometer Company, Inc., Riverside, CA).
Although the reported sensitivity for the Watermark 200SS sensor ranges from 0 - 200 kPa, erratic measurements have been reported during prolonged drying cycles exceeding 90 kPa [5] . Increased variability was suggested by authors to be due to reduced soil contact with the porous matrix. Subsequently, use of these sensors in swelling soils should be avoided [3] . More concerning for quantification of seasonal drought stress, however, is the reported failure of the sensor to respond to rapid changes in soil water [3] [5] . McCann et al. [6] reported accurate measurements during standard drying periods which were followed by complete re-wetting; however, poor results were noted under partial rewetting or rapid drying conditions. After a prolonged drying period, authors suggested accurate measurements taken during the following drying cycle would only be accurate if soil water reached or exceeded field capacity, or a threshold of −10 kPa. Furthermore, authors concluded that many deep sensors could fail to meet this re-wetting threshold and therefore these sensors could provide a limited amount of useful information for irrigation scheduling. These errors were also highlighted by Shock et al. [7] while developing calibration equations for the Watermark 200, 200SS and the 200SSX. According to other research, a minimum of 24 hours should be given after a rainfall or irrigation event to allow the sensor time to respond [8] . Although these issues may not be a concern in a well-managed irrigated cropping system [5] , the re-wetting requirement and slow response time pose significant challenges for the objective of drought quantification or under low-frequency and deficit irrigation regimes.
Still, the low sensor cost has made these sensors very appealing for the large deployments necessary for field soil water characterization. Fisher and Kebede [9] utilized the Watermark 200SS Sensor in an effort to build a very low cost canopy, soil, and air temperature monitoring device for the Mid-south region of the US. The developed monitoring device was capable of measuring each of these aforementioned parameters for under 85 USD. Measurements of soil moisture and soil, leaf, and air temperature made by this system were later shown to be capable of detecting genotypic differences in corn response to stress [10] .
Additionally, Vellidis et al. [11] utilized a 12 node, wirelessly-monitored system in a Georgia cotton field to monitor soil moisture and temperatures. Each node consisted of three Watermark sensors and up to four thermocouples. Authors suggested slight modifications in the sensor array could result in a system which could be deployed early during the growing season and remain reliable until harvest without adjustment. Results indicated deployments of 2 - 3 nodes allowed for sufficient characterization of each irrigation management zone. Authors concluded that this technology was capable of driving variable rate irrigations to fields containing multiple irrigation management zones, thereby efficiently supplying irrigation water to spatially variable water demand.
1.2. Volumetric Sensors
A large percentage of VWC sensors utilize dielectric permittivity characteristics to make inferences on soil water content of the tested medium. This dielectric measurement of soil moisture is based on the concept that air and solid mineral particles are characterized by small dielectric constants (3 - 5 for most mineral components of soils, 1 for air). These small, consistent readings greatly contrast the large dielectric constant of water (78.9 at 23˚C). Therefore, shifts in composite dielectric readings are noted even during small shifts in VWC [12] .
Several equations which range from simple to highly complex have been proposed to calculate VWC from measured composite dielectrics [13] . The most frequently used is an empirical equation outlined by Topp et al. [14] . Dielectric responses of soils, as defined by Topp et al. [14] are a function of texture, structure, soluble salt concentration, temperature, density, measurement frequency, and water content. The influence of water content on the dielectric constant is so dominant, however, that often the response of the constant can be considered “almost independent” of the other parameters [14] .
Time domain reflectometry (TDR), frequency domain reflectometry (FDR), water content reflectometery (WCR), capacitance techniques, amplitude domain reflectometry, and phase transmission techniques are all based on the composite dielectric properties of soil composite and frequently utilize some form of the Topp equation [2] [3] . These sensor types vary slightly in methodology but all characterize the water content of a very limited soil area immediately adjacent the sensor. Extrapolation from these very small spheres of influence to the field-scale is often complicated due to the spatial variability of soil characteristics. One way to compensate for this variability is to increase the number of deployed sensors, but historically, large deployments have been financially impractical.
One notable exception to this financial restriction are VWC sensors utilizing low-frequency, capacitance- based techniques [12] [15] [16] . Due to their cost, these sensors are frequently utilized for continuous logging in large deployments. Capacitance sensors correlate to soil moisture by measuring the charge time of a ground electrode buried in the soil [12] . The medium immediately surrounding the positive and ground capacitors increases or decreases charge time and this charge time is exponentially more dependent upon soil moisture than other parameters. The resulting relationship between sensor charge times and VWC is highly correlated.
One concern with relatively in-expensive capacitance sensors are their low-frequency. Low-frequency sensors are more susceptible to the dielectric constants of soil texture, electrical conductivity (EC) and temperature, and therefore shifts in readings are not as strongly associated to changes in VWC. Sensitivities to medium characteristics beyond VWC have been reported to increase below frequencies of 100 MHz [17] . Unfortunately, higher frequencies are directly related to greater cost of sensor production, and most commercially produced, low cost, low-frequency, capacitance-based sensors are below the reported 100 MHz threshold.
In an attempt to more thoroughly define the sensitivity of a low-cost, low-frequency, capacitance-based sensor, Kizito et al. [12] monitored the response of an ECH2O-TE, 70 MHz Capacitance Sensor (Decagon Devices, Inc., Pullman, WA) to changes in frequency, temperature, and EC in a wide variety of soil types. Results suggested the sensor, when used in cooperation with a generic calibration curve, was capable of accurately determining VWC while relatively insensitive to other dielectric influencing parameters. These authors also monitored changes in sensor sensitivity as frequency was altered. Substantial decreases in sensitivity to EC, temperature and soil type were noted as frequency was increased from 10 MHz to 70 MHz. Although sensitivities continued to decrease until 150 MHz, no substantial decreases were noted at frequencies higher than 150 MHz. Results are in agreement with other research by Bogena et al. [18] , who noted increases in temperature and EC sensitivity associated with a 5 MHz Decagon EC-20 sensor relative to a 70 MHz Decagon EC-5. Even so, a moderately strong temperature sensitivity of the Decagon 5TE sensor has been reported by Chávez and Evett [2] in a study comparing five commercially produced soil moisture sensors.
A variety of studies have examined the use of the low-frequency, dielectric permittivity sensors in comparison to other, more costly dielectric permittivity sensors. Czarnomski et al. [15] compared the use of a Decagon ECH2O capacitance sensors, TDR sensors, and WCR sensors to determine VWCs of undisturbed, extracted soil profiles as well as mixed soil profiles. Authors noted all three sensors failed to reasonably determine VWC with the use of standard calibration equations; however, after soil specific calibration equations were developed, relationships strengthened greatly. The only sensor significantly influenced by temperature was the ECH2O, as reported VWC decreased linearly by 0.1% for every 1˚C increase in temperature. Even so, the authors concluded after evaluating cost, accuracy, and precision that the capacitance soil moisture sensors were appropriate for studies requiring high frequency observations at multiple sites over time.
Similarly, Seyfried and Murdock [16] compared the 50 MHz Hydra Probes (Stevens Water Monitoring Systems, Inc., Portland, OR) to TDR sensors in a variety of fluids, soils, temperatures and ECs. One notable characteristic of the Hydra Probe is the unit’s ability to also measure temperature and soil EC, making the unit comparable to the Decagon 5TE sensor. Authors concluded differences between the low-frequency, capacitance sensors and the TDR sensors were due to frequency differences. Still, Seyfried and Murdock [16] reported both sensor estimated VWCs to correlate well with actual VWC under most soils.
Since the energy with which the water is held does not directly indicate amount of water held at the sampling time, conversion from matric potential to VWC requires a texture-specific soil water release/retention curve. Saxton et al., 1987 developed correlation equations between soil potentials and soil texture using a large soil hydraulic properties database. These curves and a program used to derive them have been described in detail by multiple authors [19] - [21] . Difficulties have been reported with this conversion as bulk density changes with inconsistent soil layers [2] , but strong coefficients of determination and low root mean square errors (RMSEs) have characterized some conversions of soil matric potential to VWC [22] .
1.3. Comparisons between Low-Cost Sensor Systems
Direct comparisons of similar low-cost sensors have been conducted, but construction of concrete conclusions has been difficult. Sui et al. [23] compared of Decagon EC-5 and 5TM capacitance, frequency domain sensors to Watermark 200SS granular matrix sensors in a 10 ha cotton field in Stoneville, MS. Soil texture at this site ranged from a silt to a silt loam. Sensor nodes were deployed in 10 plots and each node monitored soil moisture at 3 depths (15, 30, and 60 cm). Authors noted substantially more soil-water depletion at the 15 and 30 cm depths than at the 60 cm depth from planting until 60 days after planting (DAP). From 60 to 80 DAP, a substantial decline occurred in soil moisture at the 60 cm depth. Difficulty was noted in comparing the reported soil water potential from the 200SS and the reported VWC from the Decagon sensors. Qualitative comparisons were made by monitoring trends over time. Resulting graphs were interpreted as displaying consistent behaviors between sensors at similar depths. Authors concluded that both sensors were capable of monitoring soil water status throughout the growing season.
Similarly, Varble and Chávez [24] compared Decagon 5TE sensors with Watermark 200SS sensors under laboratory and field conditions. Measurements were then compared to VWCs determined by gravimetric sampling. Authors suggested each sensor required a unique calibration for every soil type and location within field. Although increasing soil EC in laboratory tests did not significantly influence 200SS readings, increasing soil EC did increase errors in 5TE reported VWCs. Authors concluded that field-based calibrations were more appropriate than laboratory-based calibrations, since laboratory conditions fail to represent specific, representative field operating conditions for each sensor.
Spelman et al. [25] developed calibration curves for the Decagon 10HS sensor by mixing soil at varying moisture content levels in a blender and inserting the sensor into the container. They found the manufacturer-supplied equation to be inadequate to predict soil moisture accurately. They developed a single calibration equation for use in their four primary soil types that resulted in coefficient of correlations of 0.98 and concluded that with their equation the sensor was acceptable for widespread use in southwest Florida soil types.
More information concerning the response of low-cost soil moisture sensors to VWC changes under similar soil textures and environmental conditions as those experienced in the field will be necessary before these instruments can be adopted to quantify drought our schedule irrigations. The objective of this research was to test the responses of two commercially produced, low cost soil moisture sensors to changes in water content of three dissimilar soils representing common soils in row-crop production under variable environmental conditions.
2. Materials and Methods
A container experiment was conducted at the Lon Mann Cotton Research Station in Marianna, AR during 2013. Three dissimilar soils were selected for inclusion in the study. Tested soils included an Alligator silty clay loam (34˚46'9.82"N, −90˚35'57.35"W), a Calloway silt loam (34˚44'5.72"N, −90˚45'53.81"W), and a Robinsonville sandy-loam (34˚48'26.41"N, −90˚41'5.42"W). Physical and chemical properties of these soils are described in Table 1. Prior to the initiation of the study, roughly 60 kg of each soil was dried, ground, and sieved through a number 4 mesh screen. After processing, 17 kg of each soil was placed in a plastic, 19 L container. This process was repeated three times for each soil resulting in nine total containers.
In order to allow each soil to drain, four (2 mm) holes were drilled through each container side and five (2 mm) holes were drilled through the each container base. All containers were then placed outdoors on a 4m by 4 m square cement pad elevated 1m above a grass surface. This concrete surface was selected over other natural surfaces due to its consistency and low maintenance requirements. Each container remained open to environmental conditions and was located far enough from nearby buildings to only experience shading very late during the day. Measured environmental parameters at the site included air temperature, wind speed, solar radiation, and rainfall. Soil samples were taken at the beginning of the experiment in order to determine EC and bulk density (Table 1).
Periods from saturation to near permanent wilting point (PWP) were created by either allowing rainfall to wet the containers or by pouring water into the containers. These re-wetting events occurred on 2 June, 26 June, 13 July, 12 August, and 19 September 2013. After these saturating events, the containers were left exposed to the atmosphere. If rainfall was expected, containers were covered with a plastic tarp. These practices ensured saturation was reached and a substantial, prolonged dry-down period occurred. Each container was weighed daily at 0800 CST on a Cen-Tech 130 Lb. Electric Platform Scale (Cen-Tech Inc., Camarillo, CA). Gravimetric water content was then calculated by subtracting the mass of the container and the dried soil and dividing the remaining mass by the mass of the dried soil. Volumetric water content was calculated by multiplying gravimetric water content by the bulk density determined on 25 May 2013.
Two low-cost soil moisture sensors and their associated data loggers were selected based on price and availability. These included the Decagon 10HS and Em50 Data Logger and the Watermark 200SS and Watermark 900M Monitor. The Decagon 10HS Soil Moisture Sensor Probe is a 70 MHz capacitance/frequency domain sensor. This probe also infers soil moisture by measuring the dielectric constant of the surrounding media. The output range of the unit is isolated from input voltage by an internal voltage regulator; as a result, excitation can vary from 3 - 15 V. This unit is composed of two independent probes and can also be installed into undisturbed
Table 1. Physical properties of three dissimilar soils included in this trial.
soil horizons. According to the manufacturer, this device is accurate to within ±3% VWC when utilizing the standard calibration equation. This equation is as follows:
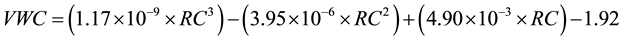 . (1)
. (1)
where: RC = raw counts reported by the sensor.
VWC = % VWC (m3/m3).
In contrast to the Decagon 10HS sensor, the Watermark 200SS sensor estimates soil water potential by monitoring electrical resistance. The 200SS consists of two electrodes placed in a granular matrix surrounded by stainless steel mesh which allows the sensor to equilibrate with the surrounding soil after installation. Although Irrometer does not state the conversion equation from resistance to soil water potential in the sensor or datalogger manual, Thompson et al. [26] indicated the manufacturer utilizes the conversion equation published by Shock et al. [7] , which the authors noted was only valid from −10 to 75 kPa. This equation is as follows:
 . (2)
. (2)
where: S = soil water potential (kPa).
R = measured resistance of the sensor (ohms).
T = temperature (˚C).
One sensor from each manufacturer was placed near the center each container within 1 cm of the soil surface in a vertical orientation. Each sensor was connected to the aforementioned data loggers produced by the same manufacturer. Data were collected from each sensor at an hourly interval and the manufacturer provided conversions were used to convert from sensor readings to either soil water potential or VWC.
Statistical analysis was conducted in JMP 11 (SAS Institute Inc., Cary, NC) and SigmaPlot 11 (Systat Software, Inc., San Jose, CA). The gravimetric water contents of each container were analyzed by a repeated measure ANOVA procedure. Parameters included date, texture, texture by date interaction, and treatment nested in replication. Replication effects were considered to be random. Subsequent relationships between sensors and soil moisture contents were compared through regression.
3. Results and Discussion
3.1. Environmental Parameters
From initiation of the study on 25 May 2013 until termination 17 Sept 2013 the buckets were covered with a waterproof tarpaulin when rain was forecasted. The buckets were then left exposed to the atmosphere. This created four investigator-manipulated, saturation-to-severe-drought stress periods and an additional, more naturally fluctuating period. The first four periods do not directly mimic typical rainfall patterns in the Mid-South but these periods are most appropriate for evaluating the aforementioned soil moisture sensors.
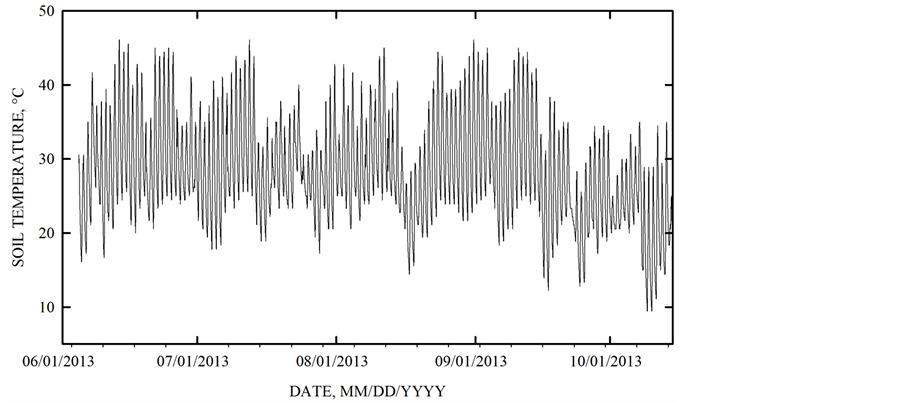
Average soil temperatures monitored every hour are displayed in Figure 1. Due to the concrete surface and the large surface area associated with each individual container, large diurnal fluctuations of soil temperatures were observed. These fluctuations are much larger than would typically be observed in row-crop agriculture, since soil temperatures within a production system are buffered by the surrounding soil and the surface area exposed to the ambient environment is greatly reduced relative to the utilized containers.
3.2. Measured Gravimetric Water Content
All tested parameters (texture, sampling time, texture by sampling time interaction, and replication) were significant (p < 0.05) (Figure 2). As expected, textural differences were evident at every measured point during the study with the largest and smallest water contents measured in the silty clay loam and sandy loams, respectively. The noted texture by date interaction is most likely a function of inconsistent differences during re-wet periods and prolonged dry-down periods. These trends can be observed in the first dry-down period, beginning on 2 June (Figure 2 & Figure 3). Immediately after the wetting event the water content of the sandy loam declines rapidly, until roughly 12 June, at which point the water content begins to decline at a much slower rate. The different rates of decline in the sandy loam are pronounced and could be fairly well characterized by two straight lines. In contrast, the silty clay loam and silt loam containers were not characterized by such a pronounced difference in the rate of decline curves.
Figure 1. Average soil temperature of the containers during the period of the study.
Figure 2. Average gravimetric water content by texture of all containers during the trial. Gravimetric water content was determined by measuring each container daily. Each point represents the mean water content calculated from three replications of each texture. Error bars represent 95% confidence intervals.
Two factors of this experiment caused much of this within-texture variability. These can best be described by considering the dry-down period to be composed of two main periods of water extraction; first, a rapid runoff/drainage event which composes the largest percentage of water loss within a few days of the water application as the soil moves between saturation and field capacity. The second period is generally dominated by evaporation and spans three or four days after the application of water as the soil moisture content decreases below field capacity. Differences in drainage characteristics within texture containers were difficult to manage, particularly in the higher shrink-swell potential silty clay loam soil. The orientation of cracks relative to the drilled drainage holes could have provided a shorter path for some applied water to exit the containers. In the silt loam and sandy loam containers, cracking was not as severe. Variability in the initial dry-down period all containers was likely influenced by differences in soil-to-drainage-hole and container-to-soil contact noted immediately after each re-wetting event (Figure 3). Additionally, non-uniform wetting within the container caused by previously
Figure 3. Gravimetric water content of the (a) three silty clay loam containers, (b) three silt loam containers, and (c) three sandy loam containers from 3 July 2013 to 1 October 2013.
described cracks or variability in moisture migration through micropores could have created moisture gradients within the containers as the soil moved from varying degrees of saturation to field capacity. During the slower, more evaporative-driven water loss period, within-treatment variability was generally more consistent; for example, as the second, third and fourth dry-down periods progressed, the third container holding the silty clay loam treatment always contained less water than the other two silty clay loam containers (Figure 3). This variability is thought to be due to slight variations in container temperatures driven by differences in intercepted solar radiation, differences in soil-container contact, etc.
3.3. Sensor Results
All nine Decagon 10HS sensors reported logical, consistent data throughout the examined time period. Trends are displayed in Figure 4. Diurnal fluctuations noted are interpreted as a function of temperature. Still, these fluctuations across such broad ranges in soil temperatures (Figure 1) are dwarfed by fluctuations in readings in response to changes in moisture content. Due to the noted significant differences in within-texture container
Figure 4. Decagon 10HS estimated volumetric water contents for the (a) silty clay loam, (b) silt loam, and (c) sandy loam containers during the trial period from 1 June 2013 to 15 November 2013.
VWC variability, it is not possible to differentiate between the variability caused by within-texture VWC differences by time and error in Decagon estimated 10HS water content. In order to isolate sensor error, individual sensor responses to measured VWC were plotted in Figure 5. Since container mass was usually measured once during a 24 hour period, the 10HS reading closest to the measurement time was used to test the relationship between estimated and actual soil moisture. The subsequent relationship of measured container VWC to 10HS estimated VWC is best predicted by a three parameter, nonlinear exponential rise to a maximum curve. Since this relationship was hypothesized to be linear, trends over time were further examined and can be seen in Figure 6. Several very important points should be given consideration. First, outside of a three or four day buffer immediately prior to and following the re-wetting events, the 10HS sensors consistently over-predicted soil moisture at most sampling points. This relationship is evident by observing the increasing divide between 10HS estimated VWC and container VWC immediately after re-wetting but prior to progression into the late secondary dry- down period. Average discrepancy between the estimated and measured VWC can be noted in Figure 6 by the separation of the average 10HS estimated VWC (straight red line) versus the average container VWC (straight black line) determined by container weight.
These large differences, which are evidently influenced by soil texture, can be best explained by non-uniform drying of the soil container. At peak soil moistures, the differences between 10HS estimated VWC and measured VWC are small. However, as the containers begin to lose water, even in the rapid dry-down period, measured VWC falls at a much faster rate than 10HS estimated VWC. As the containers move into the evaporation-dominated dry-down period, the 10HS estimated VWC remains substantially higher than the measured VWC. Differences again become minute during re-wetting events, after which the cycle resets. It is hypothesized that the small sphere of influence on the 10HS sensors relative to the large volume of soil placed in each container led to these substantial differences between absolute 10HS estimated VWC and measured VWC. One possible explanation is that there was an edge-inducted moisture gradient around the radius of the container with wetter soil in the middle and dryer soil on the outside. The sensors were generally towards the center of this radius, but as the dry down occurred, the sensors observed higher moisture content relative to the volume in the container than the average of the entire container. That is the average gravimetric moisture content would be less since most of the volume of the container is on the perimeter than in the center. This hypothesis is supported by the relationship between container VWC and 10HS estimated VWC observed in Figure 5. This is further supported by the results of Spelman [25] where they found good correlations with a Decagon 10HS when they compared sensor responses to well mixed and uniform treated soil. The proximal position of the sensor appears to buffer the estimated VWC from the more rapidly declining VWC along the more distal regions of the container. The nonlinear, exponential rise to a maximum relationship as VWC increases also supports this non- uniform drying hypothesis, since at very low moisture contents the 10HS estimated VWC and measured VWC begin to converge. This relationship is best visualized by examining the first, second, or fourth prolonged dry- down period in Figure 6. From these curves, it is evident that immediately prior to the re-wetting event the rate of container VWC decline had drastically decreased. In contrast, the rate of decline in the 10HS estimated VWC was still substantial. Given these two rates of change, it does appear that if the dry-down periods had been longer, 10HS estimated VWC and container VWC would eventually meet.
The problem of non-uniform container drying could be partially addressed by reducing the size of the tested containers to better match the sphere of influence of the tested sensors and reducing the dramatic diurnal trends in environmental conditions (mainly temperature) associated with the concrete slab by placing containers in the ground. Another approach would be to buffer the container with a larger mass, such as burying the containers in the ground rather than having them exposed above ground. Additionally, the introduction of a crop into the container may also contribute to more uniform dry-down throughout the container but this approach would not be as
Figure 5. Relationships between measured volumetric water content, where VWC = Db × Gravimetric water content, and predicted VWC by the Decagon 10HS sensors.
Figure 6. The difference between calculated VWC, derived from gravimetric water content, and the Decagon 10HS estimated water contents for the silty clay loam (a), silt loam (b), and sandy loam (c) containers. Solid reference lines represent mean differences.
desirable due to the implications increases in biomass would have on calculation of gravimetric water content. Still, it is important to note that the differences in within-container soil water contents suspected in this trial will most likely not be noted in above-ground container plant production systems.
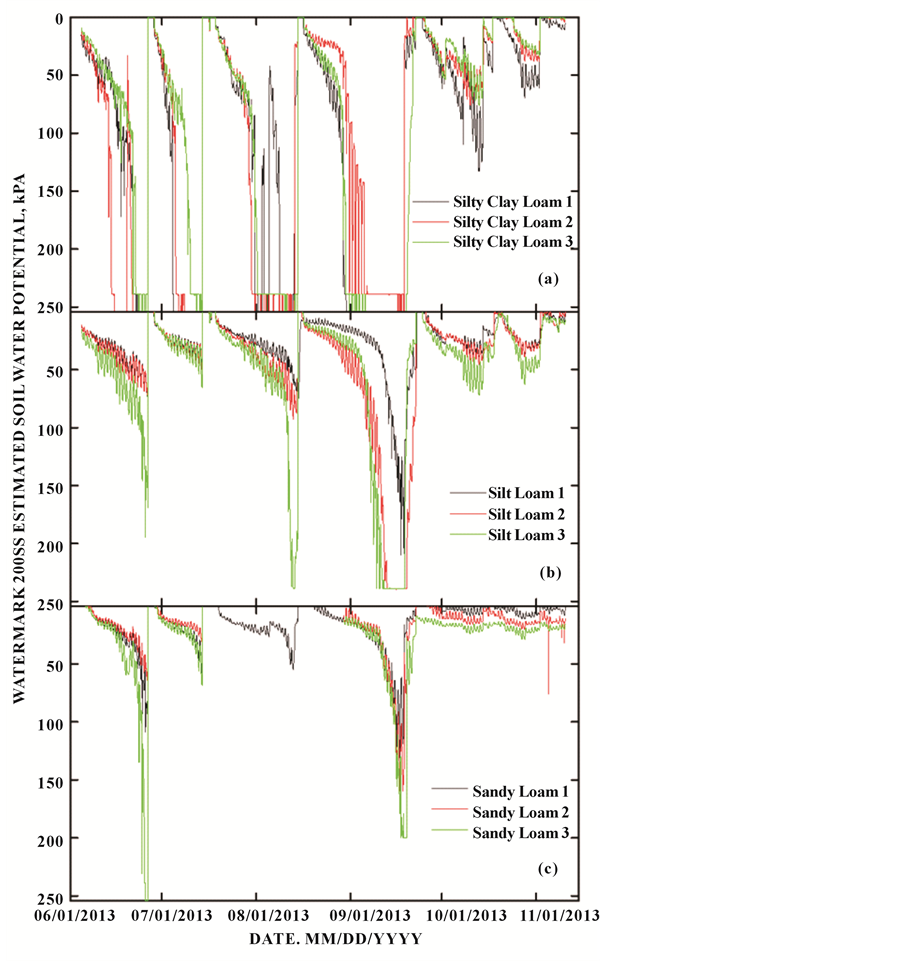
The Watermark 200SS sensor responses over time for individual containers generally followed the inverse of the container VWC (Figure 7). Diurnal fluctuations were noted from each sensor, and although temperature corrections were applied by the Irrometer datalogger, these fluctuations are interpreted as temperature-based. Still, these fluctuations associated with temperature were much smaller than observed fluctuations in readings in
Figure 7. Watermark 200SS estimated soil water potentials or the silty clay loam (a), silt loam (b), and sandy loam (c) containers during the trial period.
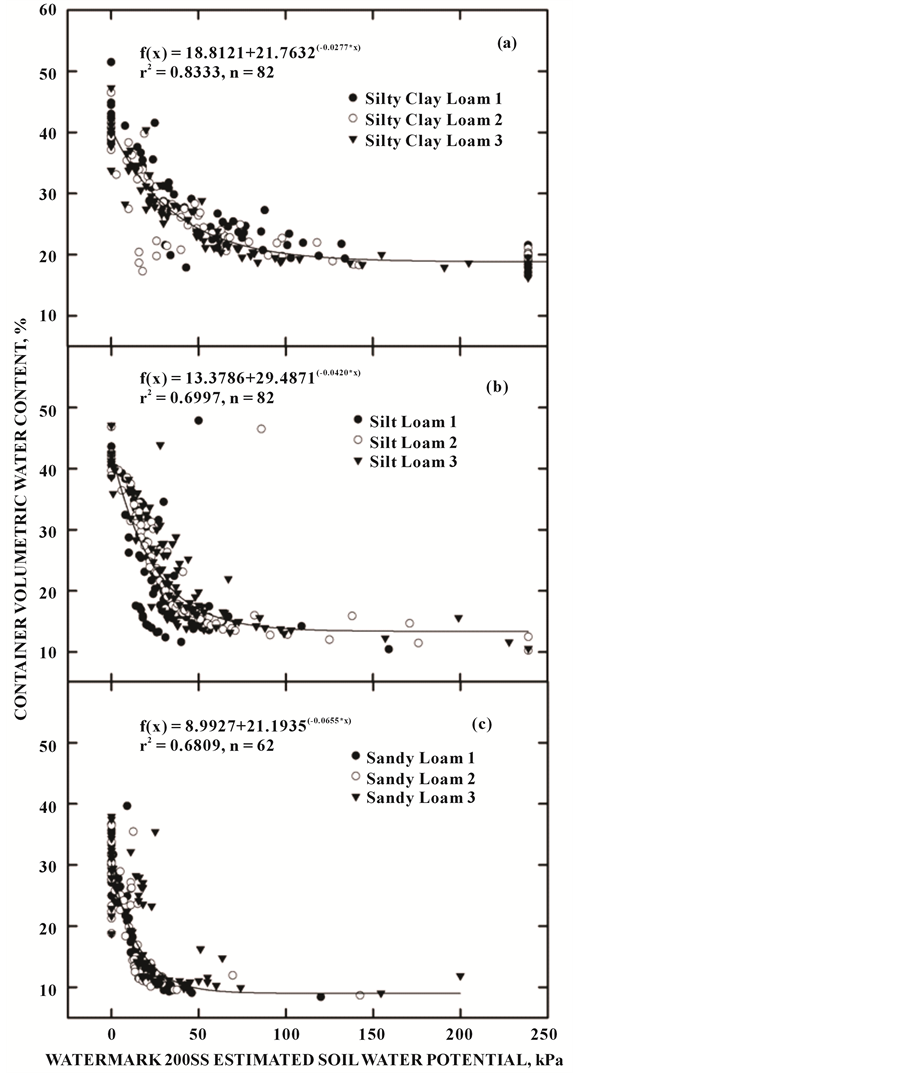
response to changes in soil moisture content. As expected, the response of each soil water potential sensor was highly influenced by soil texture (Figure 7). This response is most evident when considering the rate of soil water potential decline immediately following each irrigation event by soil texture. Watermark 200SS sensors placed in the silty clay loam containers were characterized by a very rapid decline in soil water potential which began almost immediately after the saturating event. In contrast, sensors placed in the sandy loam containers were best characterized an initial, fairly slow rate of decline followed by a much more rapid rate of decline. The initial dry-down rate was substantially slower than the silty clay loam containers; near the end of the “slow” sandy loam dry-down period at roughly 40 kPa, sensors in the silty clay loam containers had exceeded their reliable range and were near 239 kPa. Rates of declining soil water potential reported by the Watermark sensors located in the silt loam containers fell consistently between the silty clay loam and sandy loam containers. Due to this strong texture response, the sensors were grouped by corresponding texture in order to examine the response of the sensors to changes in VWC (Figure 8). Insensitivity of instruments during the initial re-wetting period noted at extreme soil water potentials did weaken the relationship between these variables some (Figure 8(a)), but these faults were associated with soil water potentials out of the reported usage ranges. More concerning, however, is the scatter of points within the reported usage ranges in the silty clay loam and silt loam containers (Figure 8(a) and Figure 8(b)). Ideally, these relationships would be more similar to the relationship
Figure 8. Relationships between container volumetric water content and Watermark 200SS sensor estimated soil water potentials graphed by tex- ture for the silty clay loam (a), silt loam (b), and sandy loam (c) con- tainers.
observed in the sandy loam containers (Figure 8(c)). These trends may be in part explained by the greater hysteresis experienced in silty clay loam and silt loam soils and issues with soil-to-sensor contact, which are generally less of an issue in coarser-textured soils.
Relationships between 10HS estimated VWCs and 200SS estimated soil water potentials graphed by texture can be found in Figure 9. The most consistent relationships between these two sensor types are found in the coarser sandy loam containers (Figure 9(c)). The much weaker relationships observed in the finer textured silt loam and silty clay loam containers (Figure 9(a) and Figure 9(b)) can be partially attributed to hysteresis of the
Figure 9. Relationship between Watermark 200SS estimated soil water potential and Decagon 10HS estimated volumetric water content for the silty clay loam (a), silt loam (b), and sandy loam (c) containers.
200SS sensor, changes in soil-to-sensor contact of both the 10HS and 200SS sensors, and slight variations in water content immediately adjacent to each tested sensor. Figure 9 highlights the narrow range of water potentials in which useful data can be collected with the 200SS sensor. Although the 200SS may perform well under near-field capacity levels of soil water and generally within the range of irrigation scheduling, another sensor, such as the 10HS, may be more appropriate for deployments designed to characterize drought stress or environmental monitoring and may be less preferable for irrigation scheduling.
4. Conclusion
The small sphere of influence on the tested soil moisture parameters coupled with the substantial evaporative demands and temperatures under which this experiment was conducted resulted in non-uniform drying of the tested containers. Subsequently, non-linear relationships were noted between 10HS estimated VWCs and actual container VWCs. Similarly, the 200SS predicted lower water potentials than calculated by converting container VWC to soil water potential. Fortunately, the preferential drying of soil in the containers in this trial will most likely not be experienced in field deployments but does highlight the disadvantage of sensors, which is that they are very susceptible to soil moisture variations irrespective of the cause. Still, the failure of the sensors to accurately predict container VWC highlights the importance of understanding the relatively small quantity of soil on which these sensors rely as well as the potential variability in soil moisture within a very limited volume. This study did indicate that texture response for the 10HS sensors was not substantial and neither the 10HS nor 200SS was highly influenced by the drastic variations in soil temperature. Further research should be conducted in weighing field lysimeters or containers which would be characterized by more uniform within-container VWCs.
Cite this paper
Tyson B.Raper,ChristopherG. Henry,LeoEspinoza,MukhammadzakhrabIsmanov,Derrick M.Oosterhuis, (2015) Response of Two Inexpensive Commercially Produced Soil Moisture Sensors to Changes in Water Content and Soil Texture. Agricultural Sciences,06,1148-1163. doi: 10.4236/as.2015.610110
References
- 1. Vories, E.D., Tacker, P.L. and Glover, R.E. (2004) Improving Cotton Irrigation Scheduling in Arkansas. In: Oosterhuis, D.M., Ed., Summaries of Arkansas Cotton Research 2003, Arkansas Agriculture Experiment Station Research Series, 521, 62-67. Fayetteville, AR.
- 2. Chávez, J.L. and Evett, S.R. (2012) Using soil Water Sensors to Improve Irrigation Management. Proceedings of the 24th Annual Central Plains Irrigation Conference, Colby, 21-22 February 2012, 187-202.
- 3. Muñoz-Carpena, R. (2004) Field Devices for Monitoring Soil Water Content. Department of Agricultural and Biological Engineering, University of Florida. Extension Bulletin 343.
- 4. Robinson, D.A., Campbell, C.S., Hopmans, J.W., Hornbuckle, B.K., Jones, S.B., Knight, R., Ogden, F., Selker, J. and Wendroth, O. (2008) Soil Moisture Measurement for Ecological and Hydrological Watershed Scale Observatories: A Review. Vadose Zone Journal, 7, 358-389.
http://dx.doi.org/10.2136/vzj2007.0143 - 5. Berrada, A., Hooten, T.M., Cardon, G.E. and Broner, I. (2001) Assessment of Irrigation Water Management and Demonstration of Irrigation Scheduling Tools in the Full Service Area of the Dolores Project: 1996-2000. Part III: Calibration of the Watermark Soil Moisture Sensor and ETgage Atmometer. Agricultural Experiment Station Technical Report, TR01-7. Colorado State University, Ft. Collins.
- 6. McCann, I.R., Kincaid, D.C. and Wang, D. (1992) Operational Characteristics of the Watermark Model 200 Soil Water Potential Sensor for Irrigation Management. Applied Engineering in Agriculture, 8, 605-609.
http://dx.doi.org/10.13031/2013.26131 - 7. Shock, C.C., Barnum, J.M. and Seddigh, M. (1998) Calibration of Watermark Soil Moisture Sensors for Irrigation Management. Proceedings of the International Irrigation Show, San Diego, 1-3 November 1998, 139-146.
- 8. Enciso, J.M., Porter, D. and Peries, X. (2007) Irrigation Monitoring with Soil Water Sensors. B-6194. Texas Cooperative Extension Service.
- 9. Fisher, D.K. and Kebede, H. (2010) A Low-Cost Microcontroller-Based System to Monitor Crop Temperature and Water Status. Computers and Electronics in Agriculture, 74, 168-173.
http://dx.doi.org/10.1016/j.compag.2010.07.006 - 10. Kebede, H., Fisher, D.K. and Young, L.D. (2012) Determination of Moisture Deficit and Heat Stress Tolerance in Corn Using Physiological Measurements and a Low-Cost Microcontroller-Based Monitoring System. Journal of Agronomy and Crop Science, 198, 118-129.
http://dx.doi.org/10.1111/j.1439-037X.2011.00493.x - 11. Vellidis, G., Tucker, M., Perry, C., Kvien, C. and Bednarz, C. (2008) A Real-Time Wireless Smart Sensor Array for Scheduling Irrigation. Computers and Electronics in Agriculture, 61, 44-50.
http://dx.doi.org/10.1016/j.compag.2007.05.009 - 12. Kizito, F., Campbell, C.S., Campbell, G.S., Cobos, D.R., Teare, B.L., Carter, B. and Hopmans, J.W. (2008) Frequency, Electrical Conductivity and Temperature Analysis of a Low-Cost Capacitance Soil Moisture Sensor. Journal of Hydrology, 352, 367-378.
http://dx.doi.org/10.1016/j.jhydrol.2008.01.021 - 13. Alharthi, A. and Lange, J. (1987) Soil Water Saturation: Dielectric Determination. Water Resources Research, 23, 591-595.
http://dx.doi.org/10.1029/WR023i004p00591 - 14. Topp, G.C., Davis, J.L. and Annan, A.P. (1980) Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resources Research, 16, 574-582.
http://dx.doi.org/10.1029/WR016i003p00574 - 15. Czarnomski, N.M., Moore, G.W., Pypker, T.G., Licata, J. and Bond, B.J. (2005) Precision and Accuracy of Three Alternative Instruments for Measuring Soil Water Content in Two Forest Soils of the Pacific Northwest. Canadian Journal of Forest Research, 35, 1867-1876.
http://dx.doi.org/10.1139/x05-121 - 16. Seyfried, M.S. and Murdock, M.D. (2004) Measurement of Soil Water Content with a 50-MHz Soil Dielectric Sensor. Soil Science Society of America Journal, 68, 394-403.
http://dx.doi.org/10.2136/sssaj2004.3940 - 17. Chen, Y. and Or, D. (2006) Geometrical Factors and Interfacial Processes Affecting Complex Dielectric Permittivity of Partially Saturated Porous Media. Water Resources Research, 42, 1-9.
http://dx.doi.org/10.1029/2005WR004744 - 18. Bogena, H.R., Huisman, J.A., Oberdorster, C. and Vereecken, H. (2007) Evaluation of a Low-Cost Soil Water Content Sensor for Wireless Network Applications. Journal of Hydrology, 344, 32-42.
http://dx.doi.org/10.1016/j.jhydrol.2007.06.032 - 19. Fredlund, D.G. and Xing, A. (1994) Equations for the Soil-Water Characteristic Curve. Canadian Geotechnical Journal, 31, 521-532.
http://dx.doi.org/10.1139/t94-061 - 20. Saxton, K.E. and Rawls, W.J. (2006) Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Science Society of America Journal, 70, 1569-1578.
http://dx.doi.org/10.2136/sssaj2005.0117 - 21. Saxton, K.E., Rawls, W.J., Romberger, J.S. and Papendick, R.I. (1986) Estimating Generalized Soil-Water Characteristics from Texture. Soil Science Society of America Journal, 50, 1031-1036.
http://dx.doi.org/10.2136/sssaj1986.03615995005000040039x - 22. Eldredge, E.P., Shock, C.C. and Stieber, T.D. (1993) Calibration of Granular Matrix Sensors for Irrigation Management. Agronomy Journal, 85, 1228-1232.
http://dx.doi.org/10.2134/agronj1993.00021962008500060025x - 23. Sui, R., Fisher, D.K. and Barnes, E.M. (2012) Soil Moisture and Plant Canopy Temperature Sensing for Irrigation Application in Cotton. Journal of Agricultural Science, 4, 93-105.
- 24. Varble, J.L. and Chávez, J.L. (2011) Performance Evaluation and Calibration of Soil Water Content and Potential Sensors for Agricultural Soils in Eastern Colorado. Agricultural Water Management, 101, 93-106.
http://dx.doi.org/10.1016/j.agwat.2011.09.007 - 25. Spelman, D., Kinzli, K. and Kunberger, T. (2013) Calibration of the 10HS Soil Moisture Sensor for Southwest Florida Agricultural Soils. Journal of Irrigation and Drainage Engineering, 139, 965-971.
http://dx.doi.org/10.1061/(ASCE)IR.1943-4774.0000647 - 26. Thompson, R.B., Gallardo, M., Agüera, T., Valdez, L.C. and Fernández, M.D. (2005) Evaluation of the Watermark Sensor for Use with Drip Irrigated Vegetable Crops. Irrigation Science, 24, 185-202.
http://dx.doi.org/10.1007/s00271-005-0009-5
NOTES

*Corresponding author.