Agricultural Sciences
Vol.5 No.7(2014), Article ID:46660,16 pages
DOI:10.4236/as.2014.57062
Comparison between Hydro-Flume and Open Field Head Ditch Irrigation Systems at Kenana Sugar Scheme, Sudan
Daffa Alla M. Abdel1, Wahab Ali M. Adeeb2
1Agricultural Engineering Section, Research and Development Department, Kenana Sugar Company, Rabak City, Sudan
2Irrigation and Water Management Institute, Gezira University, Wad Medani, Sudan
Email: dafaalla.rabih@kenana.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2014; revised 13 May 2014; accepted 30 May 2014
ABSTRACT
A study was undertaken in Kenana Sugar Scheme, Sudan during 2009/2010 and 2010/2011 seasons. In this study, the gated pipe (hydro-flume) for furrow irrigation was compared with the conventional open field head ditch irrigation system concerning the volume of irrigation water applied to the field, irrigation efficiencies, the time of cutoff, water and irrigation time saved and the irrigation production efficiency (IPE). To achieve these objectives, two commercial cane fields having the same furrow lengths (2100 m) and slopes were chosen. The study shows that in the open field head ditch irrigation, the irrigation water added was 69.1 mm in the top, 75.7 mm in the middle and 66.1 mm in the end of the furrow. Whereas, the irrigation water added in the gated pipe system was 132.7 mm, 46.1 mm and 101.9 mm, respectively. The present study indicates that the gated-pipe system has a high value of application efficiency (79% - 88%) compared with the open field head ditch (69% - 71%). The percent of deep percolation (PDP) for the gated-pipe system is greater than the PDP obtained under open field head ditch irrigation conditions. Also the percent of runoff (PRO) is higher under the open field head ditch system and the water conveyance efficiency for the open field head ditch is 88%. While the gated pipe needs more advance time but can save 20 to 65 m3 of water/irrigation cycle with better uniformity coefficient (CU) and irrigation production efficiency (IPE) compared with the open field head ditch. From the above mentioned results, it is concluded that under Kenana conditions the gated-pipe system is better than the open field head ditch irrigation system keeping in mind that for more uniform water distribution through irrigated furrows of the long fields of Kenana, increased pressure head at the inlet and/or larger openings of the hydro-flume gates may be necessary.
Keywords:Irrigation, Sugarcane, Gated Pipe, Hydro-Flume, Furrow, Application Efficiency, Percolation

1. Introduction
Surface irrigation is the most widely used irrigation method. This is due to its low capital and maintenance costs, and low energy requirements [1] . Among the many surface irrigation methods, furrow irrigation is one of the most commonly used methods. Furrow irrigation is a method of applying water at a given rate into shallow evenly spaced Canals [2] . In furrow irrigation, the field divided into sectors each of 60 furrows in which irrigation water is applied. The furrows are filled to the desired depth of water and this water is retained until it infiltrates into the soil both vertically and horizontally.
The gated pipe (hydro-flume) is defined as a closed conduct with a circular cross section with water flows inside it (no free surface). The flows result from pressure difference between inlet and outlet and they affected by fluid properties and the flow rate.
The gated pipe furrow irrigation system consists of relatively large diameter pipes of about 0.46 m (18 inches), with gates usually equipped on one side and corresponding to the furrow spacing. The hydro-flume is made of VU and thermally protected low density polyethylene of 700 micron wall thickness for maximum service life time in hot and tropical condition. It is flexible so that no alluvial clings to its wall. The gated pipes as an improvement in furrow irrigation, in which the conventional head ditch and siphon are replaced by an above ground pipe. Gated pipe was introduced to allow more uniform irrigation. Uniformity of flow is determined by setting the gates precisely to deliver equal flow into furrows, the rate of discharge in each furrow was less than with siphon tubes that induced erosion, and less leaching potential. Gated pipe also facilitates the eventual adoption of surge irrigation. Gated-pipes are currently used extensively in sugarcane fields in Upper Egypt. [3] found that using gated-pipe to irrigate long furrow resulted in saving water by 20% and 38% and increasing its use efficiency by 58% and 17% for bean and peas, respectively. [4] stated that varying pipe slope, diameter, number of gates, gate area and mean outflow, affect uniformity of outflows. They added that for the entire typical gated-pipe situation analyzed, maximum flow uniformity is obtained with the pipeline slope uphill in the direction of flow. In Sudan, the gated pipe furrow irrigation system was first introduced for vegetable production in a small scheme in Zaied Elkhair which is located on the eastern bank of the Blue Nile.
In Kenana Scheme, the gated pipe was introduced in year 2003 to allow for more uniform irrigation. The rate of discharge in each furrow was less than with siphon tubes that induced erosion, and less leaching potential. Gated pipe also facilitates the eventual adoption of surge irrigation. The system has high application efficiency when operated properly. In 2001/02, the gated pipe furrow irrigation system was adopted in Kenana Scheme for irrigating sugarcane in large scale. Until January, 2007 about 75% of the total area was serviced by the gated-pipe in place of the open field head ditch system with open canal. Recently (years 2004-2005), the gated-pipe was also adopted in some fields at Sudanese Sugar Company mainly, Asalayia Sugar Scheme.
Irrigation practice in Kenana has subjected to many changes. In year 1981, the water indenting was based on fixed days per cycle, and different sizes of siphon were used in the same field to maintain the cycle regardless of field gradient of furrow length. A irrigation system based on evapotranspiration (10 mm/day) was introduced in 1983. In 1987, an indenting system of irrigation based on the number of operating pumps was adopted. Recently, the individual fields were categorized into three groups according to their length, slops and soil classes as A, B and C system, which are irrigated every 12, 10 and 7 days respectively. The steeper the field, the shorter is the furrow length and the shorter is the irrigation cycle.
Irrigation water is pumped from the White Nile into a main canal and distributed through secondary canals until it reaches an open field head ditch from which it is siphoned through a pipe into the furrows of the field. The Scheme is provided with a drainage net work. In year 2002, the open field head ditch system has been gradually changed to the closed system. The open field head ditch and siphons are replaced by an above ground flexible pipe (Hydro-flume) of 18 inch internal diameter, 100 meter long with adjustable gates spaced at 1.5 meter interval.
1.1. Objectives of the Study
The broad objective of the present study is to study the irrigation production efficiency (IPE) produced through improving on-farm water management. The specific objective is to compare the gated pipe system for furrow irrigation with the open field head ditch system with regards to saving time of irrigation, irrigation production efficiency (IPE) and water distribution uniformity.
1.2. Open Field Head Ditch System
An open field head ditch is an open waterway whose purpose is to carry water from one place to another. Field ditches have smaller dimensions and convey water from the farm entrance to the irrigated fields. Under Kenana conditions, the most commonly used field canal cross-section in irrigation is the trapezoidal cross-section with the following dimensions (Figure 1 and Table 1).
Irrigation water is siphoned out through three or two inches internal diameter siphon tubes from the irrigation ditch. The inflow rate through the siphon tube, which is a function of the pressure head causing flow, was computed using the following formula [5] ;
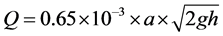 (1)
(1)
where:
Q = discharge from siphon tube (l/s).
0.65 = coefficient of discharge determined under Kenana condition, [6] .
a = area of the cross-section (cm2).
g = acceleration due to gravity (cm/s2).
h = pressure head causing flow (cm) which is the difference in elevation between the water surface in the field canal and the center of the outlet under free flow conditions or the water surface above the outlet when the outlet is submerged.
1.3. Gated Pipe Pressure and Flow
As water moves through any pipe, pressure is lost due to turbulence created by the moving water. The amount of pressure lost in a horizontal pipe is related to the velocity head, pipe diameter, roughness and the length of pipe through which the water flows. When velocity increases, the pressure loss increases.
[7] narrates the inflow rate through gated pipe with velocity as stated below;

Figure 1. A trapezoidal canal cross-section. Where; The top width of the field canal (a) =2.75 m; The top width of the water level (a1) = 1.90 m; Height of the field canal (h) = 0.70 m; Water depth in the canal (h1) = 0.30 m; Bottom width (b) = 1.15 m; Free board (f) = 0.40 m.
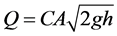 (2)
(2)
where: Q = discharge from outlet (L/S), C = coefficient of discharge. A = area of the outlet cross-section (cm2), g = acceleration due to gravity (cm/s2), h = pressure head causing flow (cm).
[8] investigated the effect of non-uniform outflow distribution along the gated-pipe and he indicated that the open field head ditch method, allow more uniform outflow distribution through siphon tubes along the open field head ditch compared to the gated pipe system, Whereas, the gated pipe allows more outlet water sets than the open field head ditch method. He added that the quantity of water outflow along the gated pipe depend mainly on the alignment and steepness of the gated pipe rather than the number of opening operating at a time or their distance from riser. Because the choice of the gated pipe furrow irrigation system was influenced by the degree of alignment of the pipeline at the field head.
1.4. Loss of Pressure
Water flowing in pipes is always accompanied by a loss of pressure due to friction and the amount of loss is due to smoothness of the inside walls of the pipe, the diameter of the pipe and the velocity of the water flow. The head loss due to friction of a pipe is determined by using [9] .
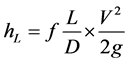 (3)
(3)
where: hL = head loss (m), f = friction factor (dimensionless);
L = pipe length (m), D = pipe diameter (m), V = Average velocity (m/s);
g = Acceleration due gravity.
The friction factor was calculated using [10] as below:
 (4)
(4)
 (5)
(5)
where: f = friction factor, Re = Reynolds number (more than 105 turbulent flow).
Q = Pipe discharge (m3/hr).
D = Pipe diameter (m).
In straight and long pipe, the loss in head which accounts for the outlets is corrected with a factor (C) suggested by [11] which is a function of the number of the outlets and the friction equation used. The Christiansen factor (C) was expressed as below:
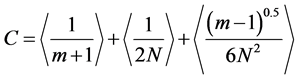 (6)
(6)
where: C = fraction of the head loss under constant outflow conditions, m = 1.85 for Hazen-Williams formula; 1.9 for the Scobey equation and 2.0 for the Darcy-Weisbach equation, N = number of outlets along the pipe.
The Christiansen factor (C) was obtained assuming the following conditions:
■ All the outlets are equally spaced.
■ All the outlets have discharge.
■ No flow at the downstream end of the gated-pipe.
■ The distance between the pipe inlet and the first outlet is equal to the outlet spacing.
2. Materials and Methods
2.1. Site Specification
2.1.1. Location
The study was conducted in the commercial cane fields of Kenana Sugar Estate, (Latitude 13˚10'N and longitude 32˚40') in heavy clay soils, with 65% clay, 24% silt, 11% sand and a pH of 7.5 - 8.5, during the seasons of 2009/200 and 2010/2011, with the purpose of comparing the gated pipe system for furrow irrigation to the open field head ditch system with regards to saving time of irrigation, irrigation production efficiency (IPE) and water distribution uniformity. Kenana Scheme is located on the eastern bank of the White Nile River, 300 km south of Khartoum at an altitude of 410 m above mean sea level (msl).
2.1.2. The Soil
Kenana Scheme extends on a clay plain, which dips very gently to the White Nile River plain. The soil is very dark-grayish-brown in color, fine in texture, quite uniform, alkaline in reaction (pH, ranges from 7.5 to 8.5). Non-saline, non-sodic. Kenana soil is characterized by a very low infiltration rate (0.00005 m3∙m−1∙min−1) and it contains about 11% sand, 24% silt and 65% clay (mainly montmorillonite). The mean soil water content (0 - 100 cm) at field water capacity was 44% and at wilting point was 20% in volume.
2.1.3. Climate Information
The area of Kenana scheme lies within the tropical dry hot semi-arid climatic zone, with a cool dry season during winter (November-February) followed by a hot dry season (April-June). The rainy season extends from July to October, with peak monthly rainfall in August. The mean annual rainfall is around 340 mm (for the period from 1977 to 2010), while the mean relative humidity 08:00 is around 58%.
2.1.4. Area of the Scheme
Kenana Scheme has a total surface area of about 67,000 hectares (180,000 feddans), only an area of 40,000 hectares (95,000 feddans) is cultivated annually. An area of 6000 hectares is annually left out as semi-fallow.
2.1.5. Irrigation Network
The irrigation network consists of six pumping stations, situated along the main canal, with a total lift of 45 m above the White Nile level. The six pumping stations are connected in series to irrigate the 40,000 hectares. Pumping stations one and two are designed to pump a maximum of 42 m3∙s−1. The other four stations are designed with less capacity because of the diversion of water to primary canals. Irrigation water in the main canal is diverted into the primary canals through gates with flow regulators. The open field head ditches are supplied by the primary canal via off-take pipes. Each open field head ditch irrigates one field, each field is split into five to seven sectors, and each sector consists of 60 furrows with 1.55 m spacing. Furrows run perpendicular to contour lines with lengths ranging from 300 to 2750 m.
2.2. Data Collection
2.2.1. Soil Data
Soil samples for gravimetric moisture determination both for gated pipe irrigation and conventional open field head ditch were collected at furrow top, middle and end for evaluating the soil moisture deficit prior to the irrigation. Soil moisture deficit is a measure of the soil moisture between field capacity and existing moisture content multiplied by the root depth, and it represents the depth of water the irrigation system should supply; which mean the required infiltration depth. At each location along the tested furrow, soil samples were monitored at 20 cm increments to a depth of 100 cm just before and 72 hours after irrigation. Then the gravimetric moisture content (w/w) were calculated and converted to volumetric values (v/v) by multiplying by the dry bulk density [12] . Then the soil moisture change was converted to the infiltrated depth at different sites of the furrow.
2.2.2. Measurement of Hydraulic Parameters
The field comparison measurements started from the third irrigation event, so that the rate of change of infiltration rates and the effect of differences in the intake opportunity times would be minimized. In each tested field a group of four consecutive furrows were tested, using as near constant pressure head as circumstances permitted in the gated pipe and the earthen open field head ditch. The inflow rate, Advance and recession phase, runoff discharge, the time of cutoff and the volume of irrigation water applied to the tested field were used to compare the hydraulic performance.
2.2.3. Measuring Inflow Rate in Gated Pipe
In the present study a graduated glass manometer was placed inside the center of the gates that is inserted into the gated pipe system for measuring the hydraulic head of the gate which equal to distance from the water level in the manometer tube to center of the gated pipe. Stop watch and graduated bucket were also used to calculate the flow rate per unit time (m3/s).
The distance of each gate from the water source (riser) was calculated by multiplying the gate number by gate spacing which is equal to 1.5 m apart. The amount of irrigation water flowing (Q) and its velocity (V) inside the hydro-flume was calculated using Toricelli equation (Equation (2)). Also the Reynolds numbers (Re) for each tested gated pipe were calculated using Equation (5) [13] and the type of water flow was also determined. Finally, the friction factor was calculated using Equation (4).
2.2.4. Advance and Recession Phase
The most important field data are the advance rates, which can vary throughout the irrigation season. The experimental procedure followed for determination of the advance trajectory was based upon the following steps:
1) Using field stakes and surveying tape, the tested furrows were divided into a number of stations having equal distances between them.
2) As the irrigation water advanced down the furrow, arrival times were recorded at the end of each reach.
When the flow area was equal to 10% of the maximum cross-sectional area, recession times were observed and recorded at each station.
2.2.5. Determination of the Infiltration Parameters (C, k and a)
An average values of 0.0001 m3/min/m furrow length, 0.446 and 0.002 for the steady-state final infiltration, C, the constants a (as the slope of the regression line) and k (as the y-intercept at time t = 1) respectively, as computed by [14] were used in this study. [15] exploits these parameters for the determination of the average infiltrated depth as stated below;
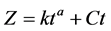 (7)
(7)
where;
Z = infiltrated volume per unit length after an infiltration opportunity time, t.
C = the basic intake rate (m3·m–1·min–1) =
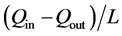 (8)
(8)
k and a = empirical fitting parameters.
Qin and Qout = the inflow and outflow rates, respectively, in m3·min–1.
L = furrow length (m).
A comparison of irrigation performance parameters between open field head ditch and gated-pipe:
2.2.6. Water Application Efficiency (Ea)
The Ea was calculated according to [16] as follows;
 (9)
(9)
where;
Ea = water application efficiency, percent.
Zreq = required depth of application.
L = field length (m).
Qo = discharge/furrow (m3/m).
tco = cutoff time (minute).
2.2.7. Percent Runoff (PRO)
Losses from the irrigation system via runoff from the field end are indicated in percent runoff;
 (10)
(10)
2.2.8. Deep Percolation Ratio (DPR)
Losses of water through drainage beyond the root zone, it is defined as:
 (11)
(11)
2.2.9. Christiansen Uniformity (CU)
In the present study the Christiansen Uniformity (CU) as computed using the following formula;
![]() (12)
(12)
where;
x = sum of the absolute deviation of individual observations from the mean value, M.
n = number of observations.
The head loss in the hydro-flume was calculated using Equation (3).
2.2.10. Conveyance Water Loss
A common open field head ditch sector of 200 m was selected for assessing the conveyance water loss. The open field head ditch was 2 m wide. A thin plate rectangular weir was used for monitoring the water flow at the water source. Then the water conveyance efficiency was calculated from the water volumes measured from two sites by the following formula [17] :
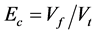 (13)
(13)
where: Ec is conveyance efficiency, Vf is volume of water delivered to the field and Vt is volume of water delivered from the source.
2.2.11. Water Saving
The water saved is referring to the consumption differences between gated pipe irrigation system and the conventional open field head ditch method.
3. Results and Discussion
3.1. Soil Moisture Content
Table 2 and Table 3 show the average values of the soil moisture content before and 3 days after irrigation for the two methods of irrigation for depth intervals of 20 cm down to one meter. Results indicated that in fields irrigated by the gated pipe system and due to the continuous wetting effect of irrigation, higher percentage of the volumetric moisture content (three days after irrigation) accumulated at the top layers of the soil. However under conventional furrow irrigation application using open field head ditch, results showed consistent soil water content at different sampling depths. The deep percolation of the soil moisture at infiltration depth below the effective root zone depth at the top of the furrows irrigated by gated pipe was mainly due to the low inflow rate (3 to 4 l/s) and the long irrigation time required to refill the root zone at the field end.
3.2. Distribution of Water Depth
Again Table 2 and Tables 3(a)-(c) present the amount of water added (infiltrated volume) for the soil profile (0 - 100 cm) in the evaluated furrows in different irrigation events (this table is a summary of 8 samples taken during the irrigation season). In the open field head ditch furrow irrigated field, the irrigation water added at the three locations was 69.1 mm at the top, 75.7 mm at the middle and 66.1 mm at the end of the furrow. Whereas, the irrigation water added using the gated pipe system at the three locations were 132.7 mm at the top, 46.1 mm at the middle and 101.9 mm at the end of the furrow, respectively.
Analyses show that (Table 3(c)) the mean difference in the volumetric soil moisture content (infiltrated volume) at the top, middle and bottom of the field using open ditch is statistically insgnificant. similar analyses performed for the infiltrated volume using gated pipefurrow irrigation system indicated that the mean difference are highly significat (P ≥ 0.5) compared to the open ditch irrigation system.
3.3. Irrigation Parameters for Open Field Head Ditch and Hydro-Flume
Tables 4-7 showed the performance evaluation of the open field head ditch and gated-pipe irrigation systems. These findings indicate that for irrigation number 7 and 11, the gated-pipe system of irrigation has a high value of application efficiency (Ea) (79% and 88%) compared with the Ea of the open field head ditch (69% and 71%). The percent of deep percolation (PDP) for the gated-pipe system is greater than the PDP obtained under open
Table 2 . Mean monthly climatic data during 2009/2010 and 2010/2011 seasons in Kenana Sugar Scheme*.
*Data taken from monthly weather reports of sugarcane research meteorological station at Kenana.
Table 3. (a) Volumetric soil moisture content (Mc) before irrigation((BI) andthree days after irrigation(AI) of the furrow irrigated using open field head ditch; (b) Volumetric soil moisture content (Mc) before irrigation (BI) and three days after irrigation (AI) of the furrow irrigated using gated pipe; (c) Summary of volumetric soil moisture content (Mc) before irrigation (BI) and three days after irrigation (AI) of the furrow irrigated using open ditch and gated pipe.
Table 5. Evaluation of the open field head ditch irrigation system (irrigation number 11). N = 0.04.
ETp* = Potential evapotranspiration.
field head ditch irrigation (Tables 4-7). This is mainly due to the fact that the deep percolation of the soil moisture at infiltration depth below the effective root zone depth at the top of the furrows irrigated by gated pipe was mainly due to the low inflow rate (3 to 4 l/s) and the long irrigation time required to refill the root zone at the field end. The present results also revealed that the percent of runoff (PRO) was higher under the open field head ditch system (20% - 31%) compared with the gated-pipe irrigation system (5% - 9%). Previous results stated that the PRO tends to be directly related to the inflow rate and inversely related to Ea. Results of the comparison between the two system shows that the gated-pipe system is better than the open field head ditch.
The infiltration profile parameters were used to calculate the Christiansen Uniformity Coefficient (CU) using Equation (12). Results showed that the CU for the gated pipe and the open field head ditch methods were equal to 70% - 76% and 79% respectively. The low value of CU was mainly due to the longer contact time which leads to spatial and temporal variations of the soil moisture distribution which is more evident at the top part and along the field irrigated with gated pipe.
3.4. Advance and Recession Phases
Results of the Advance, recession, intake opportunity time and infiltrated volume of the two systems were shown in Tables 6-9. It was observed that the intake opportunity time varied with furrow length, irrigation cycle and stage of cane growth, due to the variation of soil moisture condition before irrigation. This variation did not reflect a certain trend in both irrigation methods which implies that the fields were irrigated at random and at different available water depletion levels.
Using the gated pipe irrigation technique, the slow advance rate resulted from low water outflow (3 to 4 L/s) lead to non-uniform intake opportunity time over the field. Therefore using the gated pipe due to irrigation techTable8 Comparison of the gated pipe system for furrow irrigation (GP) with the open field head ditch (FC) in term of water and time saving.
GP = gated pipe system for furrow irrigation; FC = open field head ditch.
Table 9. Comparison of the net, gross and total water applied, cane yield and irrigation production efficiency between the two irrigation systems.
Table 10. Calculation of Reynold number, friction factors and the total head loss.
Data taken from the field management department of Kenana Sugar Scheme.
nique the advance phase should be completed as quickly as possible so that the intake opportunity time over the field will be uniform and then cut the inflow off when enough water has been added to refill the root zone. This can be accomplished with a high, but non-erosive, discharge onto the field. These options are available to solve this problem, partially:
a) Dyke the downstream end to prevent runoff;
b) Reduce the inflow discharge to a rate more closely approximating the cumulative infiltration along the field following the advance phase.
3.5. Water Conveyance Efficiency
The conventional open field head ditch water loss test (Equation (10)) shows that the water lost from 200 m study section for a 180 minute time period was 10 m3. The volume of water delivered to the field (Vf) was found to be 74 m3 and the volume of water delivered from the source (Vt) was 84 m3. Most of the water loss apparently occurred through canal leakage. The water conveyance efficiency for the open field head ditch was equal to 88%.
3.6. Water and Time Saving
Compared with open field head ditch method, the gated pipe system for furrow irrigation can reduce the irrigation quota by 20 to 65 m3/irrigation cycle depending on the pre-irrigation soil water content. The irrigation time saved when using open field head ditch system was ranging from 112 to 180 minutes per irrigation cycle depending on furrow length and the pre-irrigation soil water content (Table 8).
3.7. Irrigation Production Efficiency (IPE)
A comparison of the net, gross and total water applied, cane yield and irrigation production efficiency (IPE) between the two irrigation systems was shown in Table9 Results of the comparison indicate that the difference in the net and total irrigation water applied are highly significant (P ≥ 0.05). It was found that the field irrigated using the gated pipe system out yielded the field irrigated with open field head ditch but the difference is insignificant (P ≥ 0.05). Whereas, the obtained value of the irrigation production efficiency (IPE) of the field irrigated with gated-pipe system is statistically significant (P ≥ 0.05) compared with the IPE of the field irrigated with open field head ditch (Table 9).
3.8. Head-Loss through the Gated Pipe
In the present study the calculated friction factor (f) values (Table 10) were used for the determination of the loss in the total water head of the gated pipe. Results indicated that the magnitude of the loss in the total water head was directly related to the distance from water source (the riser). Higher head produces more water from the gates.
4. Economical Analysis
Following the results of the present study, the total irrigation cost saved for sugarcane production when using cultivar Co 6806 and irrigated when 55% to 60% of the available soil moisture is depleted (treatment D2). was determined as below.
5. Conclusions
From the results the following conclusions can be drawn;
The spatial and temporal variations of the soil moisture distribution which is more evident along the field irrigated with gated pipe resulted from prolonged irrigation time. In contrast to the gated pipe system, the open field head ditch furrow irrigation method provides more uniform water distribution along the irrigated furrows.
The present study indicates that the gated-pipe system has a high value of application efficiency (79% - 88%) compared with the open field head ditch (69% - 71%). The percent of deep percolation (PDP) for the gated-pipe system is greater than the PDP obtained under open field head ditch irrigation conditions mainly at the top part of the field due to the longer contact time of irrigation. Also the percent runoff (PRO) is higher under the open field head ditch system and the water conveyance efficiency for the open field head ditch is 88%. While the gated pipe needs more advance time, it can save 20 to 65 m3 of water/irrigation cycle with slightly lower uniformity coefficient (CU) and higher irrigation production efficiency (IPE) compared with the open field head ditch. In general, the hydro flume irrigation performance parameters are better than the open field head ditch. There are certain parameters, such as CU, which can be improved with more uniform infiltration opportunity time.
6. Recommendations
From the above mentioned results, it is concluded that, under Kenana conditions, the gated-pipe system is better than the open field head ditch irrigation system keeping in mind that for more uniform water distribution through irrigated furrows of the long fields of Kenana, increased pressure head at the inlet and/or larger openings of the hydro-flume gates may be necessary.
References
- Grillo, G., Walker, W.R. and Skogerboe, G.V. (1987) Mathematical Approach for Evaluating the Zero-Inertia Model, Surface Irrigation: Theory and Practice. Utah State University, New Jersey, 328-336.
- FAO (Food and Agriculture Organization) (1993) Small-Scale Irrigation for Arid Zones: Principles and Options. FAO, Rome.
- Raddy and Abdel-Hady, M. (1993) Project Evaluation of Irrigating System on Sandy and Calcareous Soils, Cairo.
- Smith, R.J., Watts, P.J. and Mulder, S.J. (1986) Analysis and Design of Gated Irrigation Pipelines. Agriculture and Water Management, 12, 99-115.
- Michael, A.M. (1978) Irrigation Efficiency Principles of Agricultural Engineering. Vol. 11, Jain Brothers, Jodhpur, 113-178.
- Abdel Wahab, D.M. (1996) Evaluation of Irrigation System under Kenana Condition. Annual Report of Sugarcane Research Department, Kenana Sugar Scheme, Sudan.
- Torricelli, E. (1643) Italian Physicist and Mathematician. http://en.wikipedia.org/wiki/Evangelista_Torricelli
- Abdel Wahab, D. M. (2004) Evaluation of Gated-Pipe Furrow Irrigation System under Kenana Condition. Annual Report of Research & Development.
- Darcy, H. (1845) Recherches Expérimentales Relatives au Mouvement de L’eau Dansles Tuyaux, Mallet-Bachelier, Paris. 268 Pages and Atlas (in French). http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae
- Blasius, H. (1913) Blasius Boundary Layer. Mathematical Physics, 56, 1-37. http://naca.larc.nasa.gov/reports/1950/naca-tm-1256
- Christiansen, J.E. (1942) Irrigation by Sprinkler. Agriculture Experimental Station Bulletin, 37, 1-124.
- Farbrother, H.G. (1973) Water Requirements of Crops in the Gezira. Annual Report of the Gezira Research Station, 139-172.
- Reynolds, O. (1883) An Experimental Investigation of the Circumstances Which Determine Whether The Motion of Water Shall Be Direct or Sinuous and of the Law of Resistance in Parallel Channel. Philosophical Transactions of the Royal Society, 174, 935-982.
- Abdel Wahab, D.M. (2000) Evaluation, Prediction and Optimization of Long Furrow Irrigation under Kenana Conditions. Ph.D. Dissertation, Irrigation and Water Management Institute, University of Gezira, Wad Medani.
- Kostiakov, A.N. (1932) On the Dynamics of the Coefficient of Water Percolation in Soils and on the Necessity for Studying it from a Dynamic Point of View for Purpose of Amelioration. Transactions of 6th Committee International Society of Soil Science, Russia, Part A, 17-21.
- Hart, W.E., Peri, G. and Skogerboe, G.V. (1979) Irrigation Performance: An Evaluation. Journal of Irrigation and Drainage Engineering, 105, 275-288.
- Bos, M.G. (1979) Standards for Irrigation Efficiencies of ICID. Journal of Irrigation and Drainage Engineering, 105, 37-43.


