Low Carbon Economy
Vol.3 No.1(2012), Article ID:17875,5 pages DOI:10.4236/lce.2012.31003
The Research on the Cooperation and Coordination Game in Constructing Low-Carbon Green Oil Port
![]()
Transportation Management College, Dalian Maritime University, Dalian, China.
Email: fhm468@163.com, dlmudgs531@yahoo.com.cn
Received December 5th, 2011; revised January 8th, 2012; accepted January 19th, 2012
Keywords: Oil Port; Low-Carbon Green; Cooperation; the Game
ABSTRACT
Constructing low-carbon green oil port is not only beneficial to change the present situation of Chinese oil port which has pollution problems and many risks, but also to increase the economic efficiency and improve the ability of sustainable development of low-carbon green oil port. While coordinating the cooperative relationship between each related enterprises participated in the construction of oil port low-carbon green oil port, is the important segment to build a low-carbon green oil port. This paper adopted the static game model under the asymmetric circumstance to research cooperative relations of low-carbon green oil port between the oil port enterprises and other enterprises and achieved good research achievements. The study results can provide for oil port supply chain related enterprise whether you choose cooperative strategy with the theory basis and the reference for decision.
1. Introduction
Oil port can be used as oil transport, transferring, storage base. Constructing low-carbon green oil port is not only beneficial to change the present situation of serious environmental pollutions and big risks in Chinese oil port, but also to increase and promote its economic benefits and the ability of sustainable development. The construction of low-carbon green oil port needs shipping enterprise, land transportation enterprise and storage enterprise to participate in jointly. How to coordinate the cooperation between the main bodies of the cooperation is the important segment to build a low-carbon green oil port. This paper is aimed at solving the problem.
The study on enterprises’ cooperation of constructing low-carbon green oil port in the oil port supply chain, especially on the cooperation and coordination game in constructing the low-carbon green oil port, in theory, is still in the blank stage, but as to partnership coordination theory, some scholars have done many researches. Such as: Feng DongGong (2010), Wang Xun (2008), Mahesh Nagarajan et al. (2008) introduced the theory of cooperation and coordination game to the organization and coordination mechanism. The paper presents the cooperation and coordination game model to study the harmonious relation in the cooperation [1-3]. Zhao Yingxue et al. (2010) introduced option contract, and constructed a cooperative game model of supply chain coordination relationship [4]. Zhuo XiangZhi (2010) established a symmetric and asymmetric static game model to study the instability and high failure rate in supply chain alliance partnerships [5]. Kirsten Schliephake et al. (2009), Hennart J. F. (1988), Kydd A. (2001) carried on analysis on harmonic stability of supply chain cooperative relationship respectively based on the resource theory, transaction theory and social dilemmas theory [6-8]. Shang Shiqiang (2005) constructed Nash equilibrium model to supply chain partnership, based on relational contracts and analyzed the self-execution [9]. Wang Jiuhe etc. (2007) pointed out the cooperative enterprise gained more benefit and high enthusiasm in Stackelberg model, by analyzing and comparing Stackelberg equilibrium model and the Nash equilibrium model of the port supply chain partnership, [10]. Zhao Na etc. (2009) put forward that we can be based on Agent to analyze port supply chain coordinative system [11].
In conclusion, although there are no research achievements on the cooperation and coordination game in building low-carbon green oil port, the literature research results have a good reference to this study.
In the cooperative work of constructing the low-carbon green oil port, oil port is in the key position. But it cannot complete without shipping enterprise, land transportation enterprise and the storage enterprise’s common participation. And cooperation from various ways will produce cooperation coordination game relationship. Oil port enterprises and other parties have equal status in the process. We can choose static game model under the asymmetric circumstance to analyze.
2. Oil Port and Related Enterprise’s Cooperation Coordination Game
Cooperative game model of constructing low-carbon green oil port of oil port enterprises and other enterprises in the supply chain is similar with cooperation and coordination model of oil port enterprise and shipping enterprise, and we often choose the static game model under the asymmetric circumstance to construct its cooperation relationship model. Therefore, this study only constructs cooperation and coordination model of the oil port enterprise and shipping enterprise.
2.1. Assumed Condition
1) In study of the cooperative relationships in lowcarbon green oil port, we assume that the partnership enterprises, such as oil port enterprise, shipping companies, are limitedly rational, and have certain analyzing ability. When one game party chooses one strategy, it can be rational to correctly judge.
2) When constructing the low-carbon green oil port, game party has two strategies to choose, namely “involved” and “don’t participate in”. “Involved” said enterprises will participate in the low-carbon green oil port construction, i.e. cooperation; “Don’t participate in” said enterprise will not take part in low-carbon green oil port construction, i.e. no cooperation.
3) In the process of the enterprises to participate in the construction of low-carbon green oil port mechanism, the government will give it certain subsidies.
2.2. Parameter Description
1) In the process of cooperative constructing low-carbon green oil port, if oil port enterprise A and shipping enterprise B are both involved in, then the benefit they get is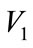 , while its benefit sharing rates are
, while its benefit sharing rates are  and
and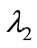 ; If oil port enterprise A or shipping enterprise B construct alone, the benefit respectively is
; If oil port enterprise A or shipping enterprise B construct alone, the benefit respectively is 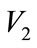 and
and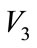 , and
, and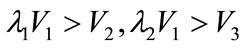 .
.
2) Set  and
and  respectively for pay costs of oil port enterprise A and shipping enterprise B in the construction of low-carbon green oil port,
respectively for pay costs of oil port enterprise A and shipping enterprise B in the construction of low-carbon green oil port, 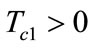 ,
,  , and
, and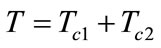 , T represents total pay cost,
, T represents total pay cost,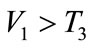 .
.
3) In the process of constructing the low-carbon green oil port, because of high environmental requirements to shipping enterprise’s berthing oil tanker, poor environmental protection shipping will be out the door of oil port enterprise. So in a certain extent it can reduce the oil port enterprise income, which can be set to S.
4) Set 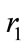 and
and 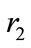 respectively for the government to the oil port enterprise and shipping enterprise subsidy rates. This subsidy rates depend on the pay cost of enterprise constructing low-carbon green oil port.
respectively for the government to the oil port enterprise and shipping enterprise subsidy rates. This subsidy rates depend on the pay cost of enterprise constructing low-carbon green oil port.
5) Set the probability of cooperation: set the probability of oil port enterprises to participate in the cooperation mechanism for x, and the nonparticipation probability is 1 − x; the probability of shipping enterprises to participate in cooperation mechanism for y, and the nonparticipation probability is 1 − y.
2.3. Modeling
Based on the asymmetric static game model, combining with cooperation mode analysis of oil port enterprises and other enterprises in the cooperation mechanism of low-carbon green oil port, and assumptions this paper set, the paper constructs cooperation and coordination relationship model of oil port enterprise and shipping enterprise. We can see this from the following Figure 1.
1) Income model of oil port enterprise. Based on the Figure 1, we can know the income model of oil port enterprise as shown in Figure 2.
Expected yields UA1 of that oil port enterprise A when it chooses to participate in cooperation construction is:
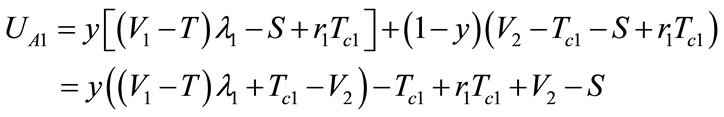
Expected yields UA2 of that oil port enterprise A when it doesn’t choose to participate in cooperation construction is: 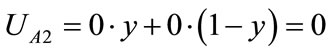
The mean income 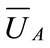 of oil port enterprise A is
of oil port enterprise A is 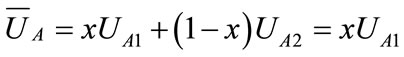
Replicated dynamic equation for earnings of constructing oil port enterprise A is:

Figure 1. Cooperation and coordination game model of oil port enterprise and shipping enterprise.

Figure 2. The oil port revenue model of the cooperation and coordination between oil port enterprise and shipping enterprise.
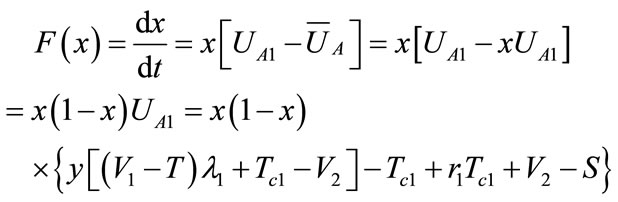
Making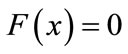 , solve
, solve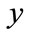 .Known: when
.Known: when
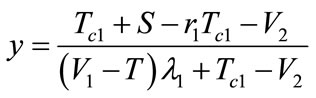 ,
, always equal zerono matter what value x takes (
always equal zerono matter what value x takes (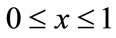 ), and the level is always in a stable state; when
), and the level is always in a stable state; when ,
,  and
and  are two stable states, but stable state also needs a certain disturbance rejection ability, namely to
are two stable states, but stable state also needs a certain disturbance rejection ability, namely to
meet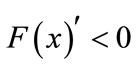 . Therefore, we need to derivate
. Therefore, we need to derivate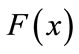 :
:
When 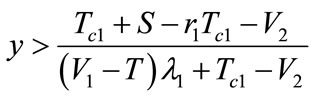
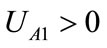 . If
. If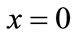 ,
, ; if
; if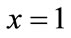 ,
,  , this is the stable state of the game model (ESS).
, this is the stable state of the game model (ESS).
When 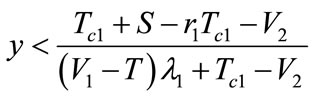
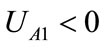 . If
. If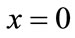 ,
, 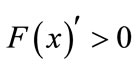 , Which is the stable state of the game model (ESS); if
, Which is the stable state of the game model (ESS); if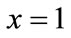 ,
,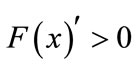 .
.
2) Shipping enterprise income model. Based on the Figure 1, we can know the shipping enterprise income model as shown in Fgure 3.
Expected yields  of that shipping enterprise B choose to participate in cooperation construction are:
of that shipping enterprise B choose to participate in cooperation construction are: 
Expected yields 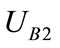 of that shipping enterprise B choose not to participate in cooperation construction are:
of that shipping enterprise B choose not to participate in cooperation construction are: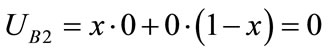 .
.
The mean income 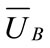 of shipping enterprise B is
of shipping enterprise B is
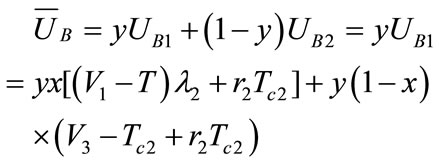
Replicated dynamic equation for earnings of constructing shipping enterprise B is:
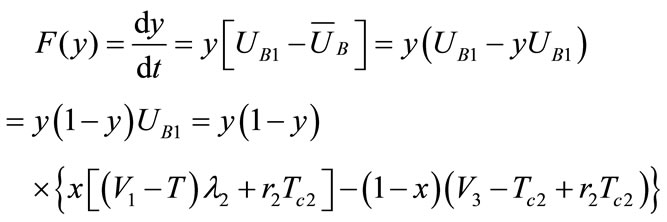
Making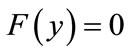 , solve x.
, solve x.
when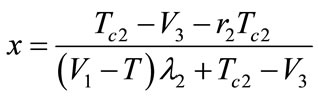 ,
,  always equal zero, no matter what value y takes (
always equal zero, no matter what value y takes ( ), the level is always in a stable state; when
), the level is always in a stable state; when
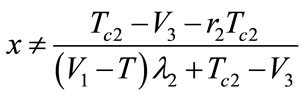 ,
, 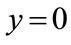 and
and 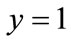 are two stable states, but stable state also needs a certain disturbance, namely to meet
are two stable states, but stable state also needs a certain disturbance, namely to meet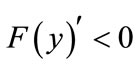 . Therefore, we need to derivate
. Therefore, we need to derivate :
:
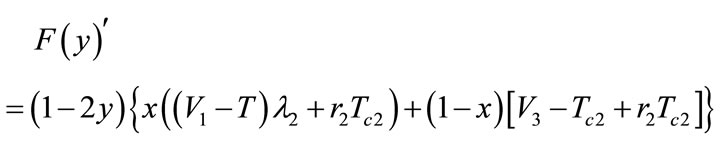
When ,
, . If
. If ,
,
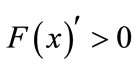 ; if
; if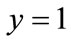 , then
, then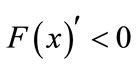 .This is the stable state of the game model (ESS).
.This is the stable state of the game model (ESS).
When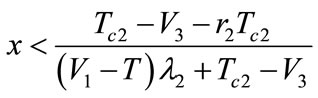 ,
, . If
. If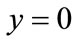 ,
,
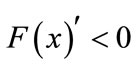 , which is the stable state of game model (ESS); if
, which is the stable state of game model (ESS); if ,
, .
.
Details use phase diagram to describe, just as shown in Figure 4.
Just as the Figure 4 shows: When the game begins, if the initial condition falls in the I area, the probability of the oil port enterprise A choosing to participate in low carbon green oil port cooperation is greater than
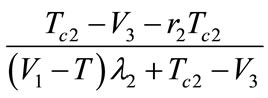 , and the probability of the shipping enterprise B choosing to participate in low carbon green oil port cooperation is greater than
, and the probability of the shipping enterprise B choosing to participate in low carbon green oil port cooperation is greater than

Figure 3. Shipping enterprise income model of cooperation coordination between oil port enterprise and shipping enterprise.
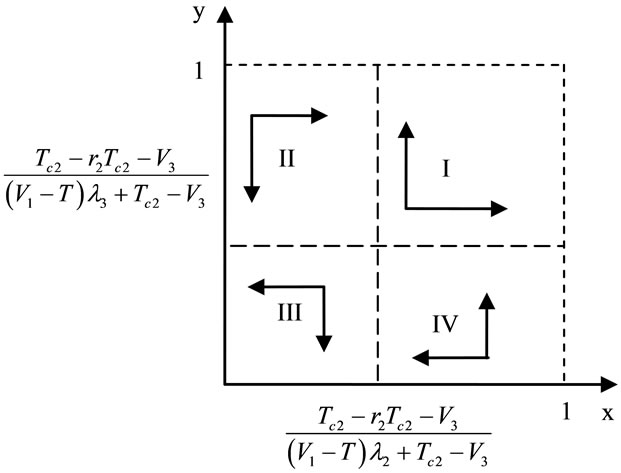
Figure 4. Replicated dynamic equation phase diagram.
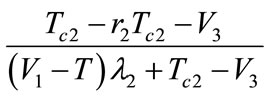 , so this game converges to
, so this game converges to ,
,
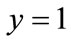 ; if the initial condition falls in the III area, the probability of the oil port enterprise A choosing to participate in low carbon green oil port cooperation is less than
; if the initial condition falls in the III area, the probability of the oil port enterprise A choosing to participate in low carbon green oil port cooperation is less than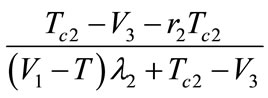 , and the probability of the shipping enterprise B choosing to participate in low carbon green oil port cooperation less than
, and the probability of the shipping enterprise B choosing to participate in low carbon green oil port cooperation less than
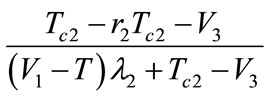 , so this game converges to
, so this game converges to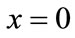 ,
,
 ; if the initial condition falls in the II area or III area, this game may converge to
; if the initial condition falls in the II area or III area, this game may converge to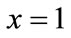 ,
, 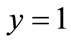 , or to
, or to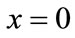 ,
, . Its ultimate equilibrium state depends on the best effort of oil port enterprise and shipping enterprise in the construction of low carbon green oil port.
. Its ultimate equilibrium state depends on the best effort of oil port enterprise and shipping enterprise in the construction of low carbon green oil port.
For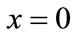 ,
, 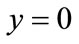 stable strategy, it means oil port enterprises and shipping companies don’t choose to participate in low carbon green oil port construction, i.e. no cooperation; for
stable strategy, it means oil port enterprises and shipping companies don’t choose to participate in low carbon green oil port construction, i.e. no cooperation; for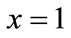 ,
, 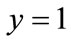 stable strategy, it means oil port enterprise and shipping companies choose to participate in low carbon green oil port construction, i.e. cooperation. Assumed that the probability of the oil port enterprise and shipping enterprise converge to
stable strategy, it means oil port enterprise and shipping companies choose to participate in low carbon green oil port construction, i.e. cooperation. Assumed that the probability of the oil port enterprise and shipping enterprise converge to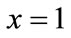 ,
,  stable strategy is p, I area
stable strategy is p, I area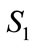 , distribution density of variable x and variable y respectively
, distribution density of variable x and variable y respectively 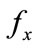 and
and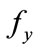 , then
, then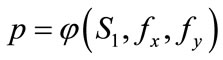 . Under the condition of variable distribution density unchanged, the greater area of I, the greater probability of the initial state in the I, the probability of the oil port enterprise and shipping enterprise converging to
. Under the condition of variable distribution density unchanged, the greater area of I, the greater probability of the initial state in the I, the probability of the oil port enterprise and shipping enterprise converging to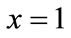 ,
,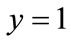 stable strategy is also bigger. Through the calculation, conclusion is:
stable strategy is also bigger. Through the calculation, conclusion is:
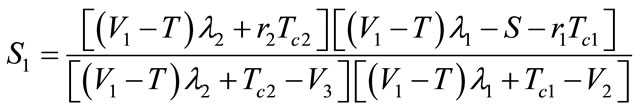 calculating the partial derivative of
calculating the partial derivative of , and assumed that game cooperation total cost T, cooperation total revenue
, and assumed that game cooperation total cost T, cooperation total revenue 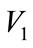 and profits K oil port enterprise and shipping enterprise got (K is a part of income
and profits K oil port enterprise and shipping enterprise got (K is a part of income 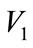 ) of both game parties, are certain, i.e.
) of both game parties, are certain, i.e.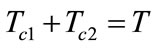 ,
, 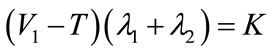 , and
, and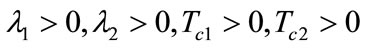 . Through calculating, gain: the probable extreme point of
. Through calculating, gain: the probable extreme point of 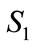 is:
is:

Therefore, when game cooperation total cost and cooperation total revenue of both game parties are certain, the contract which is most favorable to the stability of supply chain coalition should be: income distribution rate is:
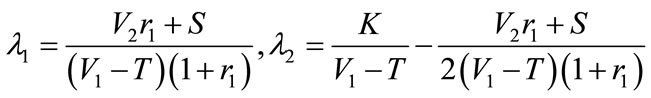 , and pay cost is:
, and pay cost is: .
.
3. Conclusion
This paper analyzes the relationship of cooperation and coordination between the oil port enterprise and other enterprises (land transportation enterprise, storage enterprise and shipping enterprise). Through the research, we know that the partnership enterprise chooses whether to cooperate is related to the size of the initial probability, when the smaller the initial probability. When the initial probability is smaller, the probability of both parties in the game tending to establish a stable cooperation is smaller, and vice versa. Therefore, the enterprise must be based on enterprise long-term interests, after much study and the careful consideration, so that it can make the decision which is beneficial to enterprise development. Research results can provide related enterprise with strong theoretical basis and decision-making reference when they choose to cooperate or not in the oil port supply chain.
4. Acknowledgements
This work was financially supported by humanities and social sciences research projects (Project number: 10YJA790045) from the Ministry of Education of P.R.C.
REFERENCES
- D. H. Feng, “Research on Port Cargo Organization and Coordination Mechanism Based on the Cooperative Game,” Dalian Maritime University, Dalian, 2010.
- X. Wang and J. X. Chen, “Game analysis of the Formation Mechanism of partnership in the Supply Chain,” Statistics and Decision, No. 7, 2008, pp. 66-68.
- M. Nagarajan and G. Sosic, “Game-Theoretic Analysis of cooperation among Supply Chain Agents: Review and extensions,” European Journal of Operational Research, Vol. 187, No. 3, 2008, pp. 719-745. doi:10.1016/j.ejor.2006.05.045
- Y. X. Zhao, S. Y. Wang, T. C. E. Cheng, X. Q. Yang and Z. M. Huang, “Coordination of Supply Chains by Option Contracts: A Cooperative Game Theory Approach,” European Journal of Operational Research, Vol. 207, No. 2, 2010, pp. 668-675. doi:10.1016/j.ejor.2010.05.017
- X. Z. Zhuo, X. Wang and Z. F. Wang, “Evolutionary Game Research of Supply Chain Coalition Partners Relationship,” Computer Engineering and Applications, Vol. 46, No. 1, 2010, pp. 208-210.
- K. Schliephake, G. Stevens and S. Clay, “Making resources Work More Efficiently—the importance of Supply Chain Partnerships,” Journal of Cleaner Production, Vol. 17, No. 14, 2009, pp. 1257-1263. doi:10.1016/j.jclepro.2009.03.020
- J. F. Hennart, “A Transaction Cost Theory of Equity Joint Ventures,” Strategic Management Journal, Vol. 9, No. 4, 1988, pp.361-374. doi:10.1002/smj.4250090406
- A. Kydd, “Trust Building Trust Breaking: The Dilemma of NATO enlargement,” International Organization, Vol. 55, No. 4, 2001, pp.801-828. doi:10.1162/002081801317193600
- S. Q. Shang and J. H. Ji, “Supply Chain Partnership Modeling and Self-Execution Analysis Based on the Relational Contracts,” Journal of Shanghai Jiao Tong University, Vol. 39, No. 3, 2005, pp. 479-483.
- J. H. Wang, “The Structure Analysis and optimization of the Port Enterprise Supply Chain,” Ph.D. Thesis, Yanshan University, Qin Huang Dao, 2007.
- N. Zhao, H. H. Zhu, H. B. Chen and G. X. Sun, “Coordination system of Port Supply Chain Based on Agent,” Marine Traffic Engineering, No. 2, 2009, pp. 57-59.

