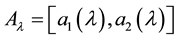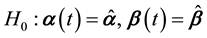Journal of Data Analysis and Information Processing
Vol.03 No.03(2015), Article ID:58425,11 pages
10.4236/jdaip.2015.33006
Fuzzy Varying Coefficient Bilinear Regression of Yield Series
Ting He, Qiujun Lu
College of Science, University of Shanghai for Science and Technology, Shanghai, China
Email: hetingfs@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2015; accepted 26 July 2015; published 29 July 2015
ABSTRACT
We construct a fuzzy varying coefficient bilinear regression model to deal with the interval financial data and then adopt the least-squares method based on symmetric fuzzy number space. Firstly, we propose a varying coefficient model on the basis of the fuzzy bilinear regression model. Secondly, we develop the least-squares method according to the complete distance between fuzzy numbers to estimate the coefficients and test the adaptability of the proposed model by means of generalized likelihood ratio test with SSE composite index. Finally, mean square errors and mean absolutely errors are employed to evaluate and compare the fitting of fuzzy auto regression, fuzzy bilinear regression and fuzzy varying coefficient bilinear regression models, and also the fore- casting of three models. Empirical analysis turns out that the proposed model has good fitting and forecasting accuracy with regard to other regression models for the capital market.
Keywords:
Fuzzy Varying Coefficient Bilinear Regression Model, Fuzzy Financial Assets Yield, Least-Squares Method, Generalized Likelihood Ratio Test, Forecast

1. Introduction
Researchers usually expect a more reliable estimate of dynamic indicators of the market data through rational design and adjustment with more flexible and applicable models when they study the financial assets price changes. The actual financial data which are often given in the form of interval are not only random but also contain fuzziness. Therefore, taking the innate fuzziness of actual financial data into account, starting with interval financial observed data and combining the features of interval financial series and finally establishing an analytical mode are big problems in analyzing assets price changes.
Since Zadeh [1] put forward the fuzzy set in 1965, the fuzzy set theory has been widely used in social science research, especially in the economic construction, financial investment, capital market operation and management etc. For interval financial observed data, Li Zhuyu et al. [2] defined the stationary of fuzzy financial time series as well as fuzzy financial assets yield series and then constructed a pth-order fuzzy auto regression (FAR) model, and also estimated the unknown coefficients by using fuzzy linear program (FLP) with satisfying the minimum fuzzy index and real meaning of financial yields. The result of estimation in [2] shows that yields convergence and fluctuation have the same trends; in addition, the model only can apply to centralized fuzzy data. This leads to deviations with the reality. In order to reflect the dynamic changes in financial yields in a period of time, Li Zhuyu et al. [4] learned the idea from D’Urso and T. Gastaldi [3] that fluctuations depended on the centers to some extent in a dynamic process, then built the fuzzy bilinear regression (FBR) model with fuzzy financial yields centers and fluctuations respectively, and estimated the unknown coefficients by fuzzy least- squares (FLS) method. Wang Donghua [5] suggested that the method of fuzzy linear program (FLP) was relatively simple so as to get a wide range result and was worse for our application.
Due to the influence of various kinds of social factors, financial asset price changes with non-linear dynamic characteristics, so the traditional method of estimation in the description of the non-linear problems tends to have larger error when modelling. Financial assets yield prediction model in literature [4] still needs to combine the explanatory ability on model, the relationship between the dynamic data, the fitting precision and prediction precision more ideally. Varying coefficient models (also called functional coefficient model) can effectively avoid the problem of the curse of dimensionality because of its obvious flexible model structure, and have a distinct advantage in exploring non-linear dynamic characteristics, reducing model specification errors, describing the features of data as well as forecasting. This article generalizes the fuzzy model in literature [4] to varying coefficient model, which is called fuzzy varying coefficient bilinear regression (FVCBR) model, by the correspondence between financial yields and the symmetric numbers used to depict its fuzziness and use fuzzy least-squares (FLS) method to deduce the estimator. Additionally, we test the adaptability of the proposed model by means of generalized likelihood ratio test. Mean square errors and mean absolutely errors are employed to evaluate and compare the fitting of fuzzy auto regression (FAR), fuzzy bilinear regression (FBR) and fuzzy varying coefficient bilinear regression (FVCBR) models, and also the forecasting of three models in and out of the sample period.
2. The Distance of Fuzzy Number Space
In order to introduce the distance of fuzzy number space, we first need to give the introduction to the symmetric numbers and its operational properties.
Definition 1 [6] . A fuzzy number
 is a fuzzy set of the real line
is a fuzzy set of the real line
 with satisfying the following conditions:
with satisfying the following conditions:
1) there exists an
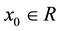 such that
such that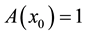 ;
;
2) for any , the
, the
 -level set
-level set
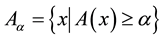 is an interval number.
is an interval number.
The set of all the fuzzy numbers is denoted by .
.
Definition 2 [6] . A fuzzy number
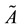 with the following membership function:
with the following membership function:
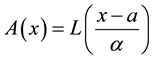 (1)
(1)
is called a symmetric fuzzy number and usually denoted by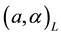 , where
, where
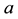
 and
and
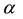
 are the center and spread of
are the center and spread of
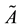 respectively. Besides,
respectively. Besides,
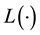
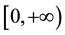
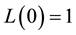
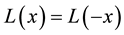
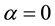
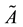

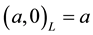
The set of all the symmetric fuzzy numbers is denoted by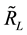
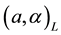
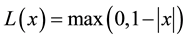
Proposition 1 [6] . Suppose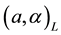
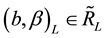
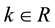
1)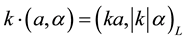
2)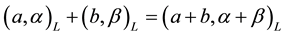
Let
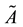
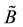
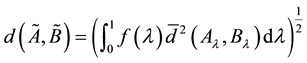
where f(λ) is an increasing function on [0,1] satisfying
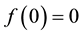
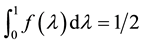
and
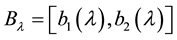
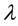
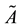
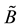
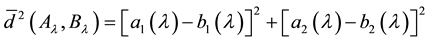
As pointed out in [7] , the monotonically increasing function
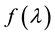
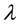
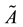
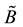

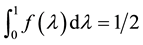
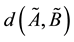
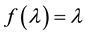
When
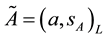
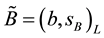
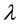
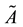

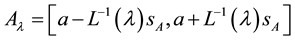
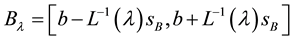
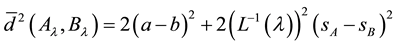
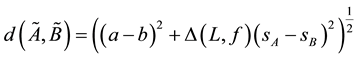
where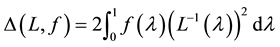
Proposition 21. If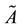
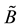
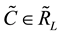

1)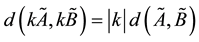
2)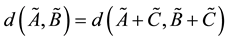
Proposition 32.
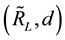
3. The Estimation and Test of Model
Suppose that
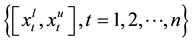
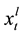
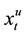
and highest prices of financial products. Fuzzy financial time series
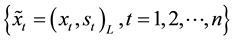
depiction of interval series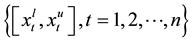
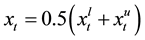
nancial product on t-th day and the series of centers

price;
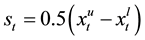
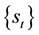
tainty of
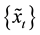
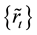
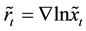
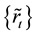
metric fuzzy numbers series
ing the following formula:
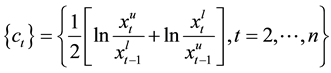
the series of spreads reflects the magnitude of nonrandomfluctuations and is expressed as following:
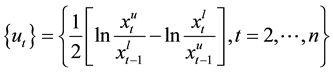
3.1. Fuzzy Auto Regression (FAR) Model
If
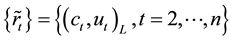
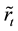
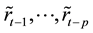
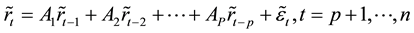
where
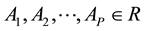

The p-th order fuzzy auto regression model has two obvious limitations, one of those is that the fuzzy auto regression as (6) will finally leads to the same trends of centers and spreads, another is that formula (6) can be equivalent to the combination of auto regression models built by two ordinary time series with centers and spreads respectively. However, only centralized data can omit the constant terms in auto regression models with traditional time series while in the common case of data, the constant terms usually cannot be ignored.
3.2. Fuzzy Bilinear Regression (FBR) Model
The fuzzy bilinear regression (FBR) model in [4] set up by the centers and spreads of fuzzy financial yields series respectively solves those two problems fundamentally.
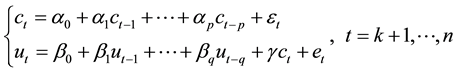
where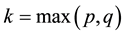

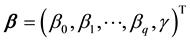
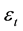
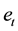
The model (7) respectively describes the auto regression relationship between the convergence of fuzzy financial yields on t-th day and the p-th order lagging value of yields, as well as the auto regression relationship between fluctuations and its p-th order lagging value. Meanwhile, the model also expresses the interdependent relationship between the fluctuations and the convergence of fuzzy financial yields. When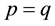

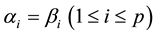

3.3. Fuzzy Varying Coefficient Bilinear Regression (FVCBR) Model
In the FAR model and FBR model, the regression coefficients being constants suggests that explanatory variables impact on explained variables constantly during the sample period. While in the study of financial assets yields prediction, the yields is a time series and the level of influence of various factors in different intervals will change. Consequently, linear models with constant coefficients are unfit for prediction and the varying coefficient models should put to use. The form of FVCBR model shows below:

In which the model coefficients are the function of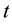
3.3.1. Coefficients Estimate of Fuzzy Varying Coefficient Bilinear Regression (FVCBR) Model
Considering the number of unknown coefficients of varying coefficient model will multiply as the sample size gets large, thus fitting models with traditional methods of estimation are not appropriate. Because of the above- mentioned disadvantages, the restricted weighted least-squares estimation is much used at present. Generally speaking, suppose that t0 is a given point in the domain of variable t, the existing observations
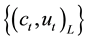
provide information to the model coefficients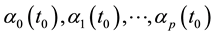
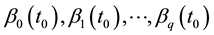
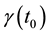
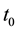
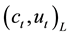
The kernel estimation is used to estimate the unknown coefficients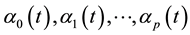
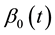
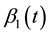


And it is minimized with respect to
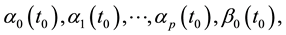
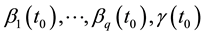
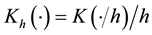
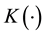
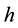
The restricted weighted least-squares problem is equivalent to minimizing the following equations:
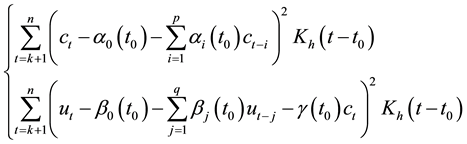
Let
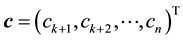
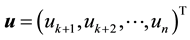
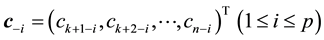
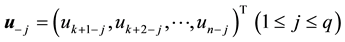
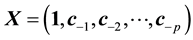
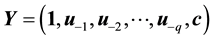
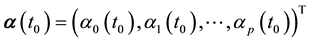
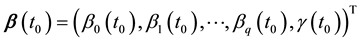
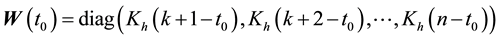
We here assume that the inverse matrix of
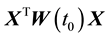
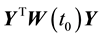
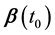
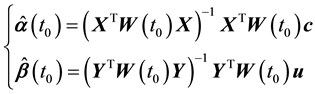
From (10) we can see the factor
If the observed values of explanatory variables are known, we can obtain the fitted values of explained variables at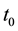

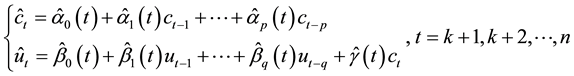
As in statistical nonparametric regression, two kinds of kernel functions are commonly used and one of them is Gaussian kernel:
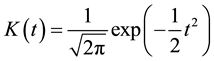
and the other is Beta kernel [8] :
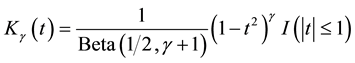
Here, we use the distance (3) used to fuzzify the cross-validation procedure [8] in statistics for selecting the optimal value of the smoothing parameter
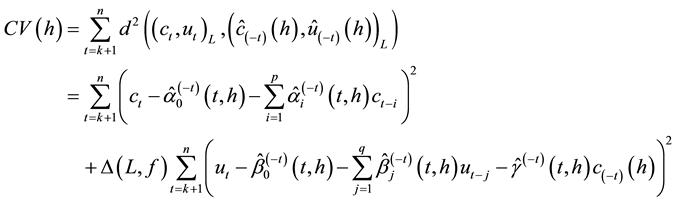
where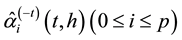
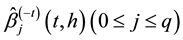
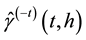
and spreads of the fuzzy coefficients under
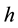
Then, select
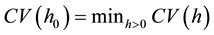
3.3.2. The Test of the FVCBR Model
As point out in [4] , FBR model can be used to analyze the fuzzy financial yields series, but whether the analysis model with constant coefficients are enough to embody the dynamic changes of yields is a question worth thinking about, that is, whether the effects of explanatory variables on explained variables will significantly change or nor as the time goes by? For that reason, we need to test the constant coefficients hypothesis, and
where

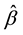
Here we use the generalized likelihood ratio (GLR) test [9] . Let
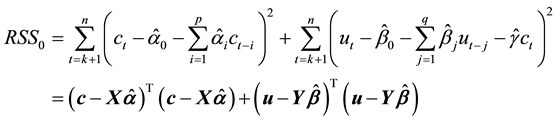
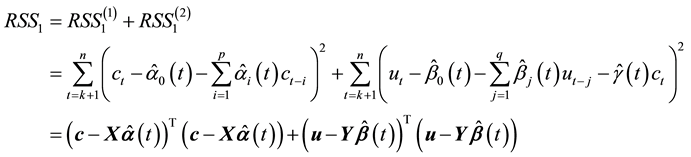
Here

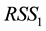
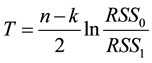
Then, the asymptotic distribution of statistic can be generalized by the method of Bootstrap. Specific steps are as follows:
Step 1. Let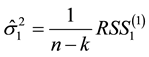
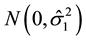
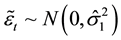

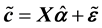
Let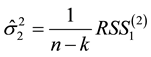
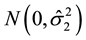
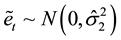


Step 2. Use the sample data to construct GLR statistics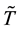
Step 3. Repeat Step 1 and Step 2 m times and then get
Step 4. The asymptotic distribution of GLR statistic
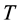
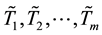
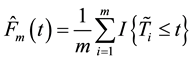
4. Empirical Analysis
Now, we will fit and forecast the fuzzy financial yields with the FVCBR model. The database consists of 119observations of the SSE Composite index from July 17, 2014 to January 9, 2015. Assume that



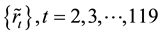
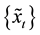


forecast samples
4.1. The Varying Coefficient Bilinear Regression Model of Fuzzy Financial Yields Series
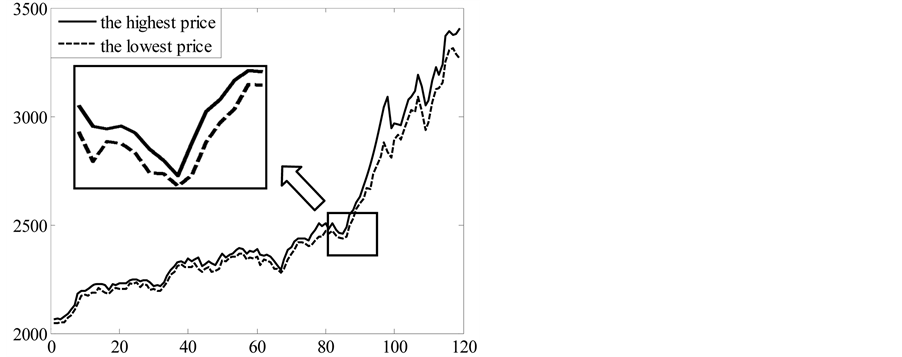
In Figure 1 we can see that the observations of the SSE Composite index
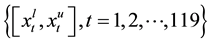
obvious increase with the time. Then, we adopt the method of run test to test the series of centers

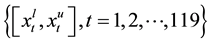
nificant level 5% suggests that the sequence of
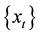

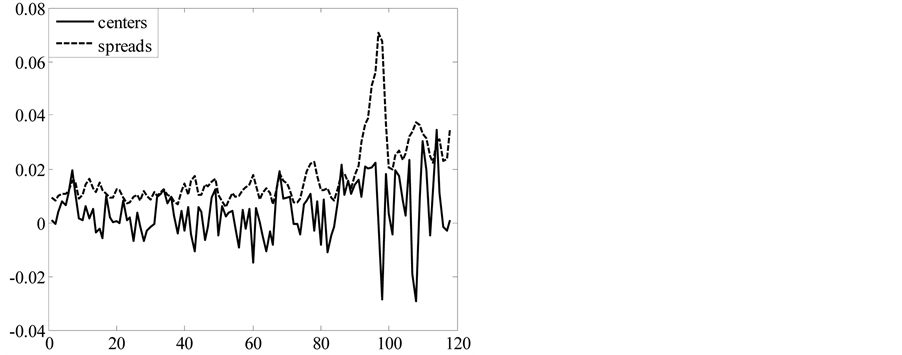
As can be seen in Figure 2, the sequence of yields
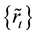
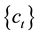
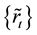

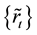
Figure 1. The series of interval observations of the SSE Composite index SSE Composite index (2014.7.17-2015.01.09) (2014.7.17-2015.01.09).
Figure 2. The fuzzy yields series of the SSE Composite index SSE Composite index (2014.7.17-2015.01.09) (2014.7.17- 2015.01.09).
Table 1. The fuzzy time series of the SSE Composite index/the run test of centers of fuzzy yields series.
Note: the test values are the averages of each sequence.
We can establish the FVCBR model for the conditional stationary financial yields
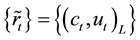
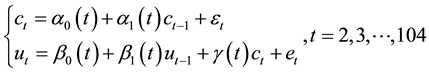
We select Epanechnikov kernel, Briweight kernel, Triweight kernel and Gaussian kernel to analysis respectively, and in turn denote above kernel functions as
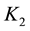

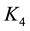

Suppose that
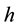
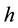
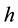
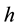
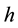
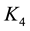
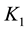

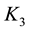
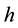
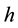
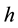
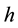
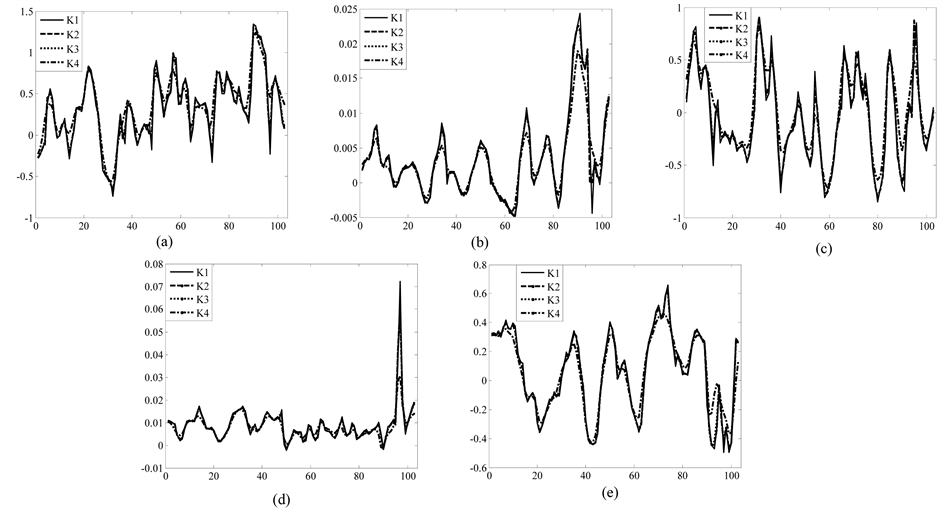
For every kernel function, we select the optimal bandwidth and then obtain the estimates of regression coefficients of model (20) at any point in time. Figure 4 shows the estimate values of regression coefficients of different kernel functions and also indicates that the regression coefficients vary similarly with the time although the different kernel functions, that is, different kernel function has little effect on the estimates values of coeffi- cients. Based on this result, we instead considering Gaussian kernel as the kernel function in this article. As we

Figure 3. The changes of CV values of every kernel function with h increasing (a) h is from 1 to 20; (b) h is from 1 to 5.
Figure 4. The estimates of regression coefficients of model (20). (a)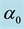
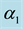
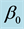
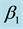

can see from the estimates of model (20) and Figure 4, the spreads of fuzzy yields have positive correlation to its first order lagging values while the relationship between the centers of fuzzy yields and its first order lagging values as well as the relationship between the spreads and current centers remain positive or negative in the dynamic changes.
Next, we will test the hypothesis of the regression coefficients are constants by using Gaussian kernel as the selected kernel function. Based on the data of SSE composite index and formula (18), we can get the generalized likelihood ratio (GLR) statistic T = 42.6781. When repeat the Step 1 and Step 2 of Bootstrap method for 100 times, that is, m = 100, the curve of asymptotic distribution of GLR statistic is as shown in Figure 5(a) and at this time the


4.2. Forecasting and Evaluation of Simulation
4.2.1. Forecasting
We forecast the real data from 105-th to 119-th with one-step-ahead prediction by using the model (20) and formula (10). The results are as shown in Table 2.
4.2.2. Evaluation of Simulation of the Model
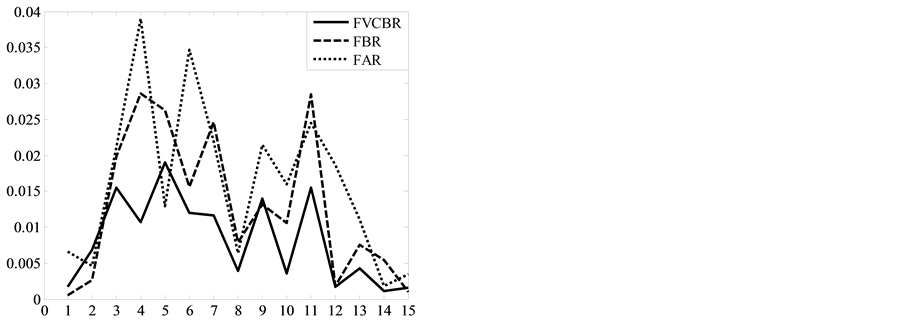
In order to compare to the prediction of FAR model and FBR model, we respectively calculate the absolute error of prediction and show them with curves (as see in Figure 6) of FAR model, FBR model and FVCBR model.
As we can see from Figure 6(a), when predict the centers, the absolute errors of FVCBR model are a little greater than FAR model and FBR model only on the 1st, the 2nd, the 5th and the 9th periods; meanwhile, when predict the spreads, the predicted values are all much close to the observed values at every period except the 1st, the 12th and the 14th periods. So, we preliminary infer that the predictions of FVCBR model are more precise than FAR model and FBR model.
For the purpose of judging the predictions and evaluations of simulation of the three models more accurately, we use the mean square error (MSE) and mean absolute error (MAE) that are often used in regression analysis to evaluate the fitting effects and prediction accuracy. Specifically, we calculate the MSE and MAE of financial yields
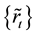

Figure 5. The asymptotic distribution of GLR statistic. (a) m = 100; (b) m = 1000.
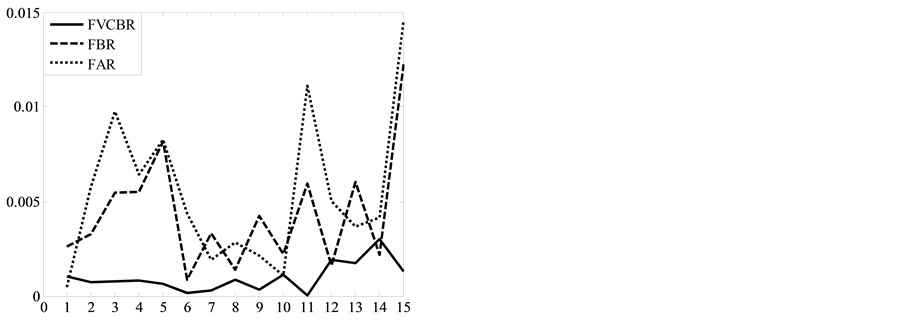
Figure 6. The comparisons of predictions of FAR model, FAR model and FVCBR model. (a) The sequence of centers; (b) The sequence of spreads.
Table 2. The results of one-step-ahead prediction of fuzzy varying coefficient bilinear regression model3.
Table 3. The errors measurements of fitting and forecasting of SSE composite index.
From Table 3, we can see no matter in and out of the sample period, the MSE and MAE of FVCBR model are all lower than FAR model and FBR model. This result proves that the fitting effects and prediction accuracy of FVCBR model are superior to FAR model and FBR model.
5. Conclusion
This article introduces the fuzzy financial yields series to deal with the interval observed samples in financial markets and constructs the fuzzy varying coefficient bilinear regression (FVCBR) model with satisfying the practical significance of financial yields. Besides, based on the complete distance between fuzzy numbers, we develop the fuzzy least squares method to obtain the estimates of the unknown coefficients. Empirical analysis shows that compared with constant coefficient regression model and fuzzy auto regression model, the varying coefficient regression has shown some improvements no matter in fitting effects or prediction. The fuzzy auto regression model has certain limitations in model fitting and forecasting because the auto regression of centers and spreads are considered independently rather than taking the effect that centers have on the spreads into account. Fuzzy varying coefficient bilinear regression explores the problem of financial fuzzy time series more flexibly and applicatively to make the fitted values and predictions be intervals and thus more consistent with the description of real financial market. Finally, this article only discusses the uncertainty of changes of financial assets price, that is, reflects the changes of yields only by fuzzy data but ignores the probability distribution of parameters. So, later research will focus on the coefficient estimates, statistical tests, model fitting and forecasting after introducing the random error, so as to give deciders more perspective to recognize and explain the changes of financial markets.
Cite this paper
TingHe,QiujunLu, (2015) Fuzzy Varying Coefficient Bilinear Regression of Yield Series. Journal of Data Analysis and Information Processing,03,43-54. doi: 10.4236/jdaip.2015.33006
References
- 1. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 2. Li, Z.-Y., Zhang, C. and Wang, T.-J. (2010) Studying on the Interval Financial Times Series and Evaluating on the Forecast. Journal of Applied Statistics and Management, 29, 129-136.
- 3. D’Urso, P. and Gastaldi, T. (2000) A Least-Squares Approach to Fuzzy Linear Regression Analysis. Computational Statistics and Data Analysis, 34, 427-440.
http://dx.doi.org/10.1016/S0167-9473(99)00109-7 - 4. Li, Z.-Y., Liu, W.-Y. and Wang, T.-J. (2009) Fuzzy Bilinear Regression of Yields Series. Statistical Research, 26, 68-73.
- 5. Wang, H.-D., Guo, S.-C. and Yue, L.-Z. (2014) An Approach to Fuzzy Multiple Linear Regression Mode Based on the Structured Element Theory. Systems Engineering—Theory & Practice, 34, 2628-2636.
- 6. Hu, B.-Q. (2010) Foundations of Fuzzy Theory. Wuhan University Press, Wuhan, 103-114.
- 7. Xu, R.N. (1991) A Linear Regression Model in Fuzzy Environment. Advances in Modelling Simulation, 27, 31-40.
- 8. Fan, J.Q. and Yao, Q.W. (2003) Nonlinear Time Series. Springer, Berlin, 243-245.
- 9. Cai, Z.W., Fan, J.Q. and Yao, Q.W. (2000) Functional-Coefficient Regression Models for Nonlinear Times Series. Journal of the American Statistical Association, 95, 941-956.
http://dx.doi.org/10.1080/01621459.2000.10474284
NOTES
1It is proved by proposition 1.
2It is proved by the density of the set of rational number in the set of real numbers.
3The regression coefficients in one-step-ahead prediction are previous estimates.