Journal of Data Analysis and Information Processing
Vol.02 No.04(2014), Article ID:51855,10 pages
10.4236/jdaip.2014.24013
Data based Calibration System for Radar used by Vehicle Activated Signs
Diala Jomaa1*, Siril Yella1, Mark Dougherty1, Karin Edvardsson2
1Department of Computer Engineering, Dalarna University, Borlänge, Sweden
2Department of Construction Technology, Dalarna University, Borlänge, Sweden
Email: *djo@du.se
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; revised 26 October 2014; accepted 18 November 2014
ABSTRACT
The accurate measurement of a vehicle’s velocity is an essential feature in adaptive vehicle activated sign systems. Since the velocities of the vehicles are acquired from a continuous wave Doppler radar, the data collection becomes challenging. Data accuracy is sensitive to the calibration of the radar on the road. However, clear methodologies for in-field calibration have not been carefully established. The signs are often installed by subjective judgment which results in measurement errors. This paper develops a calibration method based on mining the data collected and matching individual vehicles travelling between two radars. The data was cleaned and prepared in two ways: cleaning and reconstructing. The results showed that the proposed correction factor derived from the cleaned data corresponded well with the experimental factor done on site. In addition, this proposed factor showed superior performance to the one derived from the reconstructed data.
Keywords:
Vehicle activated signs, Doppler radar, vehicle velocity, experiment, calibration

1. Introduction
A range of road traffic safety solutions have been recently developed and used by public traffic agencies to ensure safety and traffic efficiency. One such traffic safety solution being investigated by traffic authorities is the Vehicle Activated Sign (VAS). VAS is a digital road sign that displays a message when a vehicle’s speed exceeds a pre-set trigger speed. At present, most existing VAS systems are static in nature. These systems have a pre-set trigger speed which is set relative to the static speed limit applied on a specific road. In certain cases, simply setting the trigger speed relative to the speed limit may not be optimal for the existing traffic conditions, thus limiting the efficiency of the VAS [1] [2] . Hence it is necessary to develop an adaptive Vehicle Activated Sign system (adaptive VAS) which will respond to traffic and road conditions. The adaptive VAS system consists of two fundamental stages: The first one is to collect accurate and significant data; whereas, the second is to automatically find the suitable trigger speed based on that data. Since the performance of the sign is sensitive to the trigger speed the ability to accurately calibrate the sign is an important factor for VAS systems. The aforementioned data could be detected by many kinds of devices, such as loop detectors, cameras, radar guns and Doppler radars. This study is concerned with the data that is mainly collected by a continuous wave Doppler radar.
The problem of data collection might seem simple and easy to achieve. In reality the problem is complex for several reasons. Firstly, since the velocities of the vehicles are acquired from a continuous wave Doppler radar, the vehicle is not travelling directly towards the radar but is slightly inclined at an angle (see Figure 1) [3] . Therefore, the radar will not measure the actual velocity, but only the relative velocity in the direction of the beam. The cosine of this angle between the radar unit and its target determines the magnitude of the error. This error is known as the cosine error and it becomes significant when the angle to the roadway is large. The greater the angle between the radar and the roadway, the lower is the indicated velocity [4] . The relationship between the measured velocity 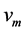 and the actual velocity
and the actual velocity 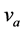 is usually expressed by the following Equation (1) [5] :
is usually expressed by the following Equation (1) [5] :
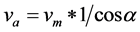 (1)
(1)
where:
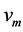 is the velocity of the vehicle detected by the radar
is the velocity of the vehicle detected by the radar
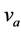 is the actual velocity of the vehicle
is the actual velocity of the vehicle
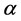 is the angle between the radar and the traveling direction of the vehicle
is the angle between the radar and the traveling direction of the vehicle
Secondly, a successful measurement requires a direct view of the radar towards the vehicles. If the radar is installed in a side fire position, the radar must be located parallel to the roadway and face the coming traffic at an angle . The distance to the oncoming lane should be between 0.5 and 3 metres. The radar is usually mounted in a side fire overhead position where the installation of the radar becomes more challenging. For this mounting, the radar must be set at a fixed height, so that its lower edge is 2.25 to 3.25 metres above the traffic lane’s ground. The radar must also be tilted to a 20˚ angle; otherwise the vehicles will not drive through the radar beam (see Figure 2). This installation is expected to be carefully set because precise alignment of the radar is the decisive factor in obtaining an exact velocity measurement and vehicle classification.
. The distance to the oncoming lane should be between 0.5 and 3 metres. The radar is usually mounted in a side fire overhead position where the installation of the radar becomes more challenging. For this mounting, the radar must be set at a fixed height, so that its lower edge is 2.25 to 3.25 metres above the traffic lane’s ground. The radar must also be tilted to a 20˚ angle; otherwise the vehicles will not drive through the radar beam (see Figure 2). This installation is expected to be carefully set because precise alignment of the radar is the decisive factor in obtaining an exact velocity measurement and vehicle classification.
Figure 1. Relation between actual velocity 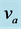 and measured velocity
and measured velocity 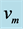 [3] .
[3] .
Figure 2. Doppler radar mounted on a sidefire overhead posi- tion and tiled to 20 degrees.
Setting the radar to a fixed height and distance can be done free from error, but eliminating errors due to the tilt of the radar to the oncoming lane is hard to achieve. Therefore measuring the angles accurately is proble- matic and requires careful measurement of road gradients and other factors. Thus, calibration has been set by subjective judgment rather than systematic judgment. In other words, the radar is typically placed at the site without a proper method and is simply set up “by eye”. A question raised in this paper is how calibration can be established with minimum equipment requirements in the field? Can a speed correction factor be derived from the available measurements collected by the radar? How can validation be completed through finding data driven by the correction factor? This paper proposes a systematic way to design an experiment for calibrating the radar with minimum requirements to be established in the field. The objective of this study is to perform a data driven calibration algorithm, which takes the data collected from two radars and derives the speed correction factor. The rationale behind using two radars is that no specialist or different equipment (or additional field personnel) are needed; once calibration has been done, the second radar can be redeployed to a new site.
The rest of the paper is organized as follows: At first, an overview about the calibration for a Doppler radar done in previous work is given in Section 2. In Section 3, data collection and experiment design are presented. Section 4 describes the calibration algorithm performed in this paper. An experiment is presented in Section 5. The results are explained in Section 6. The paper finally presents conclusions and proposes possible future studies in Section 7.
2. Related work
There are several methods that have been used in radar calibration. A common method is a tuning fork that is tuned to vibrate at a certain frequency and placed in front of the radar. This method has been previously tested and proved as a stable and suitable standard for calibrating Doppler police radar guns [6] . Another study examined the uncertainties of different methods in calibration of speed enforcement down to road radar. The proposed methods were tuning forks, a vehicle’s speedometer, speed simulators, and a fifth wheel [3] . The most uncertain method regarding vehicle speed was a vehicle’s speedometer and the least uncertain was the laboratory speed simulator. Uncertainty in the tuning fork method was approximately the same as the laboratory speed simulator. Another study developed a radar calibration system of Doppler/range radars with high precision. The developed system provides information regarding several parameters, such as the Doppler frequency shift, the frequency measured with a universal time interval counter, the emulated speed, and the weather conditions [7] and [8] . Due to the measurement error of frequency that directly affects the measured velocity, a new radar based velocity measuring system, based on a processor, was incorporated instead of calibrating the radar used in the their study. This system uses the Doppler principle based on underlying hardware design [9] . Furthermore, another study proposed a new vehicle speed and traffic flow measurement radar to get higher resolutions in speed and traffic flow management. This study is based on eliminating the interference of other vehicles on the road when detecting a certain vehicle [10] . A data fusion of Doppler radar with video camera had been proposed for a traffic surveillance system which was capable of automatically monitoring all vehicle speeds [11] . A majority of the work reported above considered a calibration method based on either comparing radar frequency or developing new calibration systems and to the best of our knowledge none have considered a data driven calibration. Data driven calibration methods were used in various traffic models such as speed-density model [12] and time gap model [13] .
3. Data collection and Experimental Design
A test site on Mjälga roadway in Borlänge, Sweden was selected for the experiment. No external factors, such as the presence of bends, junctions or roundabouts were present to affect the consistency of the data collection. The meaning of data consistency is that each vehicle which travels along the test site should be present in the data set. Since the aim of this study was to calibrate the radar used in the adaptive VAS system, two main components form the data collection system: VAS and three Siersega radars. The VAS used in the current study displays two warning messages in succession. The first is a reminder of the posted speed limit, which is 40 km/h, which is followed by a “SÄNK FARTEN” (reduce speed) message. Typically the messages are displayed only when the vehicle speed exceeds a pre-set threshold speed, i.e. the trigger speed.
The Siersega device is an advanced traffic counter. It consists of a Doppler radar sensor integrated by a Flash RAM data memory, a real time clock, a serial data interface and a battery pack. Individual vehicle data was collected by the Siersega placed across the roads 100 m before the VAS (Position A), at the site of the VAS (Position B) and 60 m after the VAS (Position C) (see Figure 3). The device at Position A is labelled as 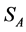 and the devices at Positions B and C are labelled as
and the devices at Positions B and C are labelled as 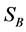 and
and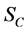 respectively. On each occasion that the Siersega recorded a time, the velocity, the direction of travel and the vehicle type for each individual vehicle for 24 hours a day for a whole week.
respectively. On each occasion that the Siersega recorded a time, the velocity, the direction of travel and the vehicle type for each individual vehicle for 24 hours a day for a whole week.
Data from the radar at the VAS is matched with data collected by two other radars installed at a distance of 60 meters and 100 meters on either side of the VAS (see Figure 3) for further analysis. Note that such radars are placed appropriately to cover the vehicles’ prior and posterior VAS velocities.
In addition, several test runs were carried out by the research team by driving a car on the road segment where the radars are installed; to be able to work out the baseline difference in the velocities reported by the radars as opposed to velocity of the car. Such difference has further been used to validate the correction factor obtained in this work (see Section 6). At this point it is worth mentioning that the baseline difference will be referred to as the experimental correction factor from this point forward. The experimental correction factor in the current case is equal to 1.18.
4. Calibration
Calibration in the current case is mainly based on mining the data collected and finding the distance correction factor. The distance correction factor is the ratio between the actual distance and the distance derived from the two radars. Figure 4 is an overview of the proposed calibration system. Data is preliminary explored to be able to detect discrepancies in the radar detection (see Section 4.1). Data is then preprocessed in two stages; detection and correction respectively (see Sections 4.2.1 and 4.2.2). Finally each individual vehicle is matched to calculate the correction factor that will be based on the distance travelled between the radars (see Section 4.3).
4.1. Data exploration
In ideal conditions, the radars should detect each vehicle and each vehicle should be visible to all of the three radars established on the road. In the real world the detection of the vehicles is often sensitive to some disturbances and this might lead to presence of missing values and outliers. At this point it is worth mentioning that the radars
Figure 3. Location of radars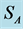 ,
, 

Figure 4. The stages of the calibration system.
should be time synchronized where the individual travel time is the time difference between the synchronous radars. However, there can be a delay between the radars’ clocks due to an incorrect setup of the clocks. Despite the radars being synchronized initially, the clocks may be delayed due to disturbances in the radar detection of the vehicle. The most challenging disturbance is the arrival of vehicles from different directions at the same time and at the same position. This means that the radar may be occupied by another vehicle passing from the other direction. Besides, overtaking and double counting can also contribute to the presence of missing values and outliers. Figure 5(a) presents a sketch showing vehicles and their corresponding times at different locations. Suppose Vehicle 













































Case 1: Vehicle 



Case 2: Vehicle 



4.2. Data preprocessing
Traffic data collected in real time often suffers from incomplete and noisy data. Data pre-processing was therefore employed to eliminate noisy data and also to be able to repair missing data [7] . Pre-processing in the current case deals mainly with detection and correction tasks respectively (see Sections 4.2.1 and 4.2.2).
4.2.1. Detection
In this step, three types of detections are of concern:
A. Detection of time delay
B. Detection of outliers
C. Detection of missing values
A. Detection of time delay
The detection of a time delay is first extracted from the data set by using a numerical algorithm. The fixed point iteration method is one of these algorithms that can be used in order to obtain an estimate as to the time delay between radars. The algorithm converges at a fixed point under some conditions given by the theorem described by previous mathematical study [14] . Based on the aforementioned study, the proposed algorithm starts at any point and recursively approaches to an approximate solution. In this paper, an optimal time delay 
1) Start by an initial value to time delay
2) Choose threshold

Figure 5. Sketch of the detection problem (a) Vehicle 









3) Calculate the estimated distance,
4) Derive expected error
5) Calculate a new time delay
6) If

7) If
where












B. Detection of outliers
At this point it is worth mentioning that detection of outliers mainly relies on understanding statistical data. Most of the outliers are usually detected by using either basic descriptive statistics, such as mean, median and standard deviation, or by visualizing the data using appropriate plots, such as scatter plots or box plots. Both show the mean prevalence of the value in the data. It should be noted that any record that significantly differs from the mean is considered as an outlier. In this work, vehicles traveling at a velocity that is higher or lower than the mean velocity relative to the data are regarded as outliers. For example, the common velocity of a motorcycle or truck differs from the common velocity of a car. Therefore data was grouped into four smaller groups based on the type of vehicle to aid in the detection of outliers. Grouping is based on the length of vehicles detected by the radar as follows:
Class 1: Motorcycle (length < 2 m)
Class 2: Cars (length >= 2 & length < 6 m)
Class 3: Trucks (length >= 6 & length < 9.5 m)
Class 4: Long trucks (length >= 9.5 & length < 25.5 m)
Based on this classification, the box plot in the figure below shows the outlier detection. The main idea is to obtain only vehicles with minimum standard deviation from the overall mean velocity. Larger variations in vehicle velocity provide inconsistency in the correction factor that will be derived later in this study. The first plots in Figure 6(a) are the velocities of vehicles respective to the four classes detected by Radar 
sign). The second plot in Figure 6(b) presents the velocities of vehicles respective to the four classes detected by Radar 



Figure 6. Vehicle velocities respective to Class 1 (motorcycle), Class 2 (cars), Class 3 (trucks) and Class 4 (trucks with trailers). (a) At radar


Radar 
C. Detection of missing values
In the current work detection of missing values mainly relies on the disturbance of radar detection which has been explained in an earlier section. Detection is therefore done by calculating the time gap. The time gap is the time difference between two successive individual vehicles. Matching is done based on these time gaps. If the difference between the time gaps is insignificant, a missing value is present. The difference is compared to a user defined threshold that cannot exceed 20 seconds. The threshold is chosen, after some in-field trials, based on the average max time gap that may occur between vehicles.
4.2.2. Correction
After the detection of the location of missing values and outliers in the data set, the data is corrected in two ways:
・ Data cleaning: The data is cleaned by removing records that are detected as outliers and missing values. After this stage, the data contains only the records that are matched with the lowest vehicle variation.
・ Data construction: The data is completely constructed by filling in missing records and keeping all outliers. The main idea of the data construction is to build a complete data set without missing any individual vehicle. The best estimate of the missing value is derived from the time and velocity of the vehicle passing from the opposite direction.
4.3. Matching and correction factor
The basic idea is to find the velocity obtained by the radar by calculating the expected distance travelled by the vehicles. For instance, time records from Radar 



where:












Figure 7. Histogram for vehicle velocities. (a) At radar



5. Analysis
The calibration system presented in previous section (see Section 4) is tested on two data sets:
・ Data Set 1: Data Set 1 was collected by Radar 

・ Data Set 2: Data Set 2 was collected by Radar 

As explained earlier (see section 4.2.1), the optimal time delay between the deployed radars should be first noticed. Figure 8 shows the optimal time delay obtained from the numerical algorithm proposed in earlier section. Note that the optimal value is reached when the time delay is approaching the minimum value that the algorithm can provide.
In Figure 8(a), the time delay between Radar 







Figure 9 and Figure 10 show the matched velocities for vehicles from Data Set 1 and Data Set 2, respectively. In Figure 9(a) and Figure 10(a), the data is cleaned by removing records of missing occurrences. In Figures 9(b) and Figure 10(b), the data is reconstructed to fill in missing data.
6. Results and Discussion
The results of the proposed correction factors are depicted in Table 1. The proposed correction factor is performed on both data sets prepared on either cleaning the data or constructing the data. Note that in the table below, the distance between 




where:
xa is the actual distance between radars
xm is the estimated distance used in Equation (4)
Results obtained clearly indicate that the correction factor obtained after data cleaning was much closer to the reference correction factor than the one obtained through data reconstruction. A fitted linear regression and goodness of fit (R-squared) to identify the relationship between the matched velocities has also been investigated. The fact that the R-squared value for the cleaned Data set 2 is higher when compared to Data Set 1 further reinforces our findings (see Table 1). Note that the correction factor is even closer to the reference correction factor and the normalized root mean squared error(NRMSE) is low when the distance between the radars is equal to 60 meters in particular, cleaned Data Set 2. A good discussion about NRMSE can be found elsewhere [17] . The fact that the proposed correction factor reported using cleaned Data Set 2 is closer to the experimental correction factor (see Section 3) i.e. 1.18, further supports the findings.
Table 1. Comparison between different correction factors, NRMSE and R-squared respective to Data Set 1 and Data Set 2.

Figure 8. (a) The optimal time delay between Radar 




Figure 9. Matching velocities for vehicles travelling between Radar 


Figure 10. Matching velocities for vehicles travelling between Radar 

7. Conclusion and future work
In this paper, a data based calibration system was applied to accurately correct vehicle velocity collected by a Doppler radar and used on the adaptive VAS system. A data driven system entails an ability to preprocess the gathered data and to match individual vehicles to find out the correction factor for vehicle velocities detected by radar. In fact, the correction factor is the ratio for the actual vehicle velocities to the measured velocities by the radar. In this study, the proposed correction factor, extracted directly from data collected by two Doppler radars placed at a pre-set distance apart, corresponds well to the true correction factor derived from the experimental calibration at the site. The proposed correction factor obtained from the cleaned data also showed more superior performance than that from the reconstructed data, indicating that filling the missing values with an estimated time and velocity provided an inaccurate data set. An estimation of time and velocity for missing values could be improved with an intelligent prediction algorithm to get further accuracy of the reconstructed data. However, the study reveals the correction factor for vehicle velocity which allows avoiding dealing with the mounting problem of the Doppler radar. The validation performed is rather a comparison with the experiment on site. Another type of validation needs to be established and explored to ensure the accuracy of the calibration system. One plausible way of testing the accuracy is by comparing the calibration system against a baseline method such as a tuning fork. Testing the system at other test sites also needs to be done in further studies.
In the near future, an adaptive fuzzy inference system can be developed to calibrate radar installation. The input to such a system can be the distance of the road, the mounting height and the tilted angle and the output is the correction factor. Also, a real time video surveillance algorithm can facilitate the detection of vehicles, the classification of vehicle types, the accurate counting of vehicles and the time difference between records. Using the real time surveillance algorithm, individual vehicles can be definitely tracked where many types of radar can be calibrated simultaneously. Monitoring and voice recording systems can be another way to calibrate the radar by analyzing the voice signals detected from the traffic. A mobile application can be a good tool to calibrate the radar on site. A mobile phone application can make it easier to track the time and velocity at a certain location using the phone’s GPS. Finally, a VAS can be developed in a way that is automatically adapted to the location by using artificial intelligence techniques.
Acknowledgements
The authors thank SafeX for their generously help in collecting the data particularly in radar maintenance and sign movement from one site to the other. Our thanks are also extended to Westcotex for their valuable technical support for server communication with the radar and data logger, Borlänge authority for allowing us to change test sites and Vectura for offering radars to the experiment. Indeed we thank Intelligent Transport System, ITS Dalarna for supporting this research.
References
- Jomaa, D., Yella, S. and Dougherty, M. (2013) Review of the Effectiveness of Vehicle Activated Signs. Journal of Transportation Technologies, 3, 123-130. http://dx.doi.org/10.4236/jtts.2013.32012
- Rämä, P. and Kulmala, R. (2000) Effects of Variable Message Signs for Slippery Road Conditions on Driving Speed and Headways. Transportation Research Part F: Traffic Psychology and Behaviour, 3, 85-94. http://dx.doi.org/10.1016/S1369-8478(00)00018-8
- Jendzurski, J. and Paulter, N.G. (2009) Calibration of Speed Enforcement Down―The Road Radars. Journal of Research of the National Institute of Standards and Technology, 114, 137-148. http://dx.doi.org/10.6028/jres.114.009
- Grakovski, A., Ovchinnikov, V. and Kamenchenko, S. (2010) Acoustic Signals Processing and Appliance for the Problem of Traffic Flow Monitoring. Transport and Telecommunication, 11, 4-10.
- Goodson, M.E. (1985) Technical Shortcomings of Doppler Traffic Radar. Journal of Forensic Sciences, JFSCA, 30, 1186-1193.
- Dujmich, L.C. (1980) Radar Speed Detection: Homing in on New Evidentiary Problems. Fordham Law Review, 48, 1138-1164.
- Fernandez, J.R.O., Briso-Rofriguez, J.C., Calvo-Gallego, J., Burgos-Garcia, M., Perez-Martines, F. and Arana-Pulido, V.A. (2012) Doppler Radar Calibration System. IEEE A&E Systems Magazine, 27, 20-28.
- Weil, C.M., Camell, D., Novotny, D.R. and Johnk, R.T. (2005) Across the Road Photo Traffic Radars: New Calibration Techniques. Proceedings on 15th International Conference on Microwaves, Radar and Wireless Communications MIKON, 3, 889-892.
- Sattibabu, G., Sridevi, C.H., Siva, S.P.T. and Ganika Sridevi, S. (2012) Design of Velocity-Measuring System with Doppler Radar Concept and FFT Algorithm Based on ARM Processor for Traffic Safety. International Journal of Advanced Research in Electronics and Communication Engineering, 1, 22-27.
- Zhang, J. (2009) The Traffic-Flow Detection Based on Pseudo-Random Coded Radar. Proceedings on International Conference on Measuring Technology and Mechatronics Automation, 9, 630-632.
- Roy, A., Gale, N. and Hong, L. (2011) Automated Traffic Surveillance Using Fusion of Doppler Radar and Video Information. Mathematical and Computer Modelling: An International Journal archive, 54, 531-543.
- Jiang, Z., Li, S.B. and Liu, X.Q. (2012) Parameters Calibration of Traffic Simulation Model Based on Data Mining. Journal Transportation System Engineering and Information Technology, 12, 28-33.
- Kant, D.S., Balaji, P. and Shriniwas, A.S. (2012) Time Gap Modeling Using Mixture Distributions under Mixed Traffic Conditions: A Statistical Analysis. Journal Transportation System Engineering and Information Technology, 12, 72-84. http://dx.doi.org/10.1016/S1570-6672(11)60233-X
- Daili, N. (2008) Numerical Approach to Fixed Point Theorems. International Journal of Contemporary Mathematical Sciences, 3, 675-682. http://dx.doi.org/10.1016/j.trb.2005.10.002
- Dion, F. and Rakha, H. (2003) Estimating Dynamic Roadway Travel Times Using Automatic Vehicle Identification Data for Low Sampling Rates. Transportation Research Part B, 40, 745-766.
- Wei, S., Jian, W., Bai-gen, C. and Qin, Y. (2003) A Novel Vehicle Detection Method Based on Wireless Magneto-Re- sistive Sensor. Proceedings on 3rd International Symposium on Intelligent Information Technology Application, 3, 484-487.
- Armstrong, S.J. and Collopy, F. (1992) Error Measures for Generalizing about Forecasting Methods: Empirical Comparisons. International Journal of Forecasting, 8, 69-80. http://dx.doi.org/10.1016/0169-2070(92)90008-W
NOTES
*Corresponding author.



























