Journal of Data Analysis and Information Processing
Vol.2 No.1(2014), Article ID:43253,7 pages DOI:10.4236/jdaip.2014.21003
Dealing with Empty and Overabundant Answers to Flexible Queries
Department of Information Technology, FATEC-SP/CEETEPS, São Paulo, Brazil
Email: samyr.moises@fatec.sp.gov.br, slago@fatecsp.br
Copyright © 2014 Samyr Abrahão Moises, Silvio do Lago Pereira. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Samyr Abrahão Moises, Silvio do Lago Pereira. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 22, 2013; revised December 28, 2013; accepted February 6, 2014
KEYWORDS
Relational Database; Fuzzy Logic; Flexible Query; Empty Answer; Overabundant Answer
ABSTRACT
In traditional database applications, queries intend to retrieve data satisfying precise conditions. As a result, thousands of data can be retrieved (overabundant answer) or, even worse, no data at all (empty answer). In both cases, the queries must be reformulated to produce more significant results and, typically, many related queries are submitted by a user before he can be finally satisfied. To overcome these problems, this paper proposes a unified solution in the framework of flexible queries with fuzzy semantics. This solution, based on the concept of semantic proximity and implemented in a tool for flexible query answering, allows the automatic reformulation of queries with empty or overabundant answers.
1. Introduction
In traditional database applications, the queries submitted by a user are rigid and intend to retrieve data satisfying precise conditions [1]. As a result, the user can obtain tens of thousands of data or, even worse, no data at all. In the former case, the user can be overwhelmed because he has no means of deciding what is the best answer; and, in the latter, he can be frustrated because he has no answer. In both cases, the user tends to reformulate his queries in order to obtain a more significant result. Thus, typically, many related rigid queries are submitted by a user before he can be finally satisfied [2].
To overcome these problems, many works in literature propose the use of flexible queries [3-5], that is, queries with vague conditions whose semantics is based on fuzzy logic [6]. In this setting, each answer retrieved by a query has a satisfaction degree between 0 and 1. More precisely, the result of a flexible query is a set of all answer satisfying, in some degree, the vague conditions imposed by the query. Clearly, the advantage of this approach is that the chance of obtaining an empty answer set is reduced and, by sorting an overabundant answer set in decreasing order of satisfaction degree, the selection of the best answer is simplified. Even though, flexible queries are not sufficient to completely avoid these problems.
In fact, there are situations where no available data can satisfy a flexible query with degree greater than 0 (Empty Answer Problem—EAP). Most of the solutions to EAP proposed in the literature are based on automatic relaxation [7-10], that is, the weakening of the predicates used in a vague condition, to obtain a less restrictive variant of it. On the other hand, there are also situations where a huge amount of data can satisfy a query with degree equal to 1 (Overabundant Answer Problem—OAP). The very few solutions to OAP proposed in the literature are based on automatic intensification [11,12] that is, the strengthening of the predicates used in a vague condition, in order to obtain a more restrictive variant of it.
As pointed out in many works, the major challenge in solving EAP (or OAP) is to find a form of relaxation (or intensification) that preserves, as much as possible, the semantics of the original query submitted by the user. As we have noticed, since relaxation and intensification are inverse transformations, no unified solution to EAP and OAP has been proposed in the literature. Thus, this also seems to be a challenge in solving these problems.
In this paper, a transformation based on the concept of semantic proximity [13] of fuzzy predicates is proposed. The main advantage of this transformation is its capability of dealing with both problems (EAP and OAP), while maintaining, as much as possible, the semantics of the original query submitted by the user.
The rest of this paper is organized as follow: Section 2 presents a fuzzy semantics for flexible queries; Section 3 proposes a unified solution to EAP and OAP, based on the concepts of semantic proximity and query modification; Section 4 describes a tool implemented for flexible query answering, based on the solution proposed in this work; Section 5 presents the conclusions of this paper.
2. Semantic Model for Flexible Queries
This section presents a fuzzy semantics for flexible queries and some illustrative examples.
2.1. Fuzzy Sets and Fuzzy Logic
Let U be a universe of discourse. A fuzzy set F in U is characterized by a membership function µF:U ® [0,1]. The value µF(x), for each x Î U, denotes the membership degree of x in the fuzzy set F.
In fuzzy logic, the semantics of a predicate is based on the concept of fuzzy set and is defined by a membership function. Moreover, the semantics of a compound fuzzy formula is derived from the semantics of its predicates and logical connectives (Ù and Ú), usually defined by minimum t-norm and maximum s-norm [14].
There are many standard membership functions which can be used to define the semantics of a fuzzy predicate (e.g., sigmoidal and Gaussian) [3]. However, due to its computational simplicity, the trapezoidal function is the most commonly used in practice. In fact, only symmetric trapezoidal functions are used in this work.
A symmetric trapezoidal function, with argument x and fixed parameters b, c and d, is defined as follows:
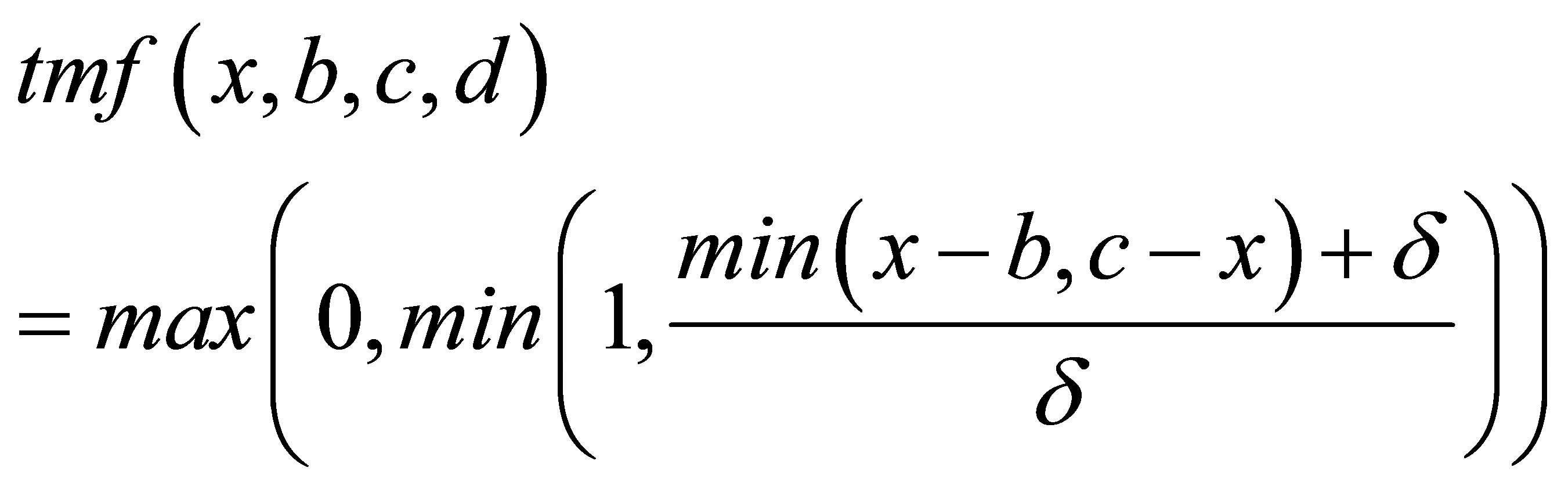 (1)
(1)
Let µT = tmf(x, b, c, d) be a symmetric trapezoidal function. The core of µT is the set of all x such that µT(x) = 1, that is, core(µT) = [b, c]. The support of µT is the set of all x such that µT(x) > 0, that is, supp(µT) = [b - d, c + d]. The boundary of µT is the set of all x such that 0 < µT(x) < 1, that is, bnd(µT) = supp(µT) - core(µT). The α-cut of µT is the set of all x such that µT(x) ³ α, for 0 £ α £ 1. If b = c, then µT is called triangular function. In this case, the core of µT has a single element, called prototype of µT.
2.2. Vague Conditions and Flexible Queries
A simple vague condition is a fuzzy predicate that takes as argument the value of an attribute in a relational database table. For example, considering a table with attributes salary, age and budget, the following simple vague conditions can be defined:
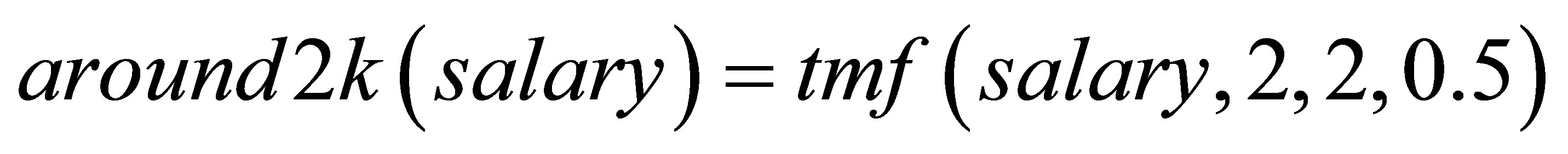 (2)
(2)
 (3)
(3)
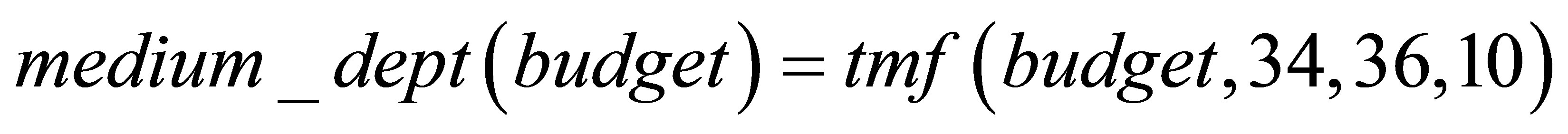 (4)
(4)
For instance, around2k(1.7) expresses the proposition “US$ 1.7(K) is a salary around US$ 2(K)”. Analogously, about_fourty(39) expresses the proposition “39 years is about 40 years” and medium_dept(23) expresses the proposition “a department with budget of US$23(K) is a medium one”. The interpretation of these predicates is shown in Figure 1.
Notice that the choice of a particular membership function to define the semantics of a fuzzy predicate is very subjective, but always must take into account the human intuition in the context of application.
The truth degree of a simple vague condition is the value of its membership function. For instance:

Figure 1. Semantics of simple vague conditions.
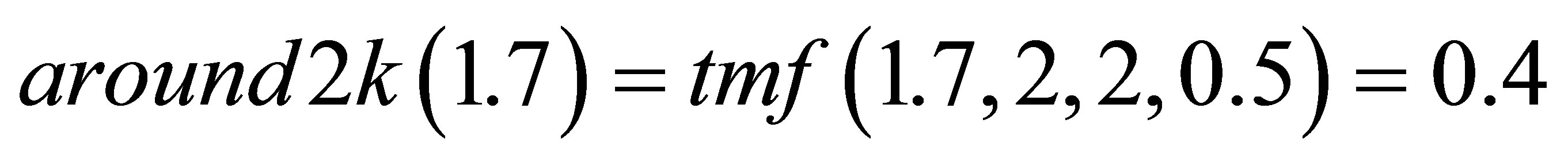 (5)
(5)
 (6)
(6)
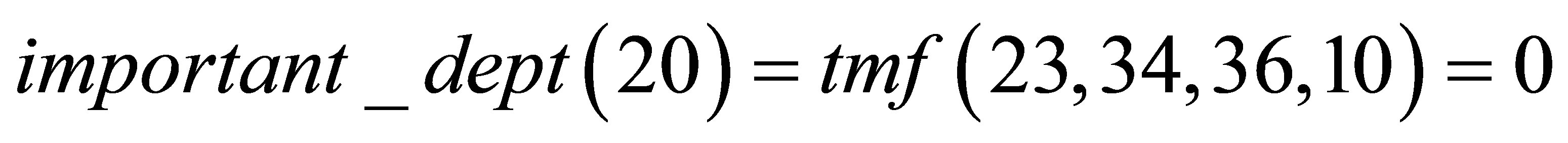 (7)
(7)
Therefore, the condition around2k(1.7) is partially true (truth degree of 0.4); about_fourty(39) is completely true (truth degree of 1); and the condition medium_dept(23) is completely false (truth degree of 0).
A complex vague condition is a formula composed of fuzzy predicates and connectives (e.g., conjunction and disjunction). The truth degree of a complex vague condition is the value of its formula. In this work, the value of A Ù B is defined as min(A, B) and the value of A Ú B is defined as max(A, B). Thus, for example, the value of the complex condition around2k(1.7) Ù about_fourty(39) is min(0.4, 1) = 0.4; and the value of the complex condition about_fourty(39) Ú medium_dept(20) is max(1, 0) = 1.
A vague condition can be a simple or a complex vague condition. A flexible query is a query with a vague condition. The answer set for a flexible query is the set of all data satisfying its vague condition, at least in some degree. Therefore, in order to avoid that a flexible query retrieves too many data with very low truth degrees, frequently an α-cut value is specified as a flexible query parameter. In this case, only data with degrees greater than or equal to α are retrieved.
2.3. An Illustrative Example
To illustrate the use of flexible queries, an example adapted from [11] is considered. This example concerns a table of employees with four attributes (i.e., name, salary, age and budget), as shown in Table 1.
In the first scenario, the user needs to retrieve data of employees who earn salary around US$ 2(K). Thus, he submits a flexible query with vague condition around2k. As shown in Table 2, this query is completely satisfied by Dupont (truth degree of 1), but it is only partially satisfied by Martin (truth degree 0.4). The remaining answers are not significant (truth degree 0).
In the next scenario, the user needs to retrieve data of employees who work in a medium department and are about forty years old. Thus, he submits a flexible query with vague condition “medium_dept Ù about_forty”. However, as shown in Table 3 no available data can satisfy this query with degree greater than 0. Indeed, this is the very situation referred as the EAP.
In the last scenario, the user submits a flexible query with vague condition medium_dept, in order to retrieve data of employees who work in a medium department. However, as shown in Table 4, a “huge” amount of the available data (relatively to the size of the table) satisfies this flexible query with degree equal to 1 and the user has
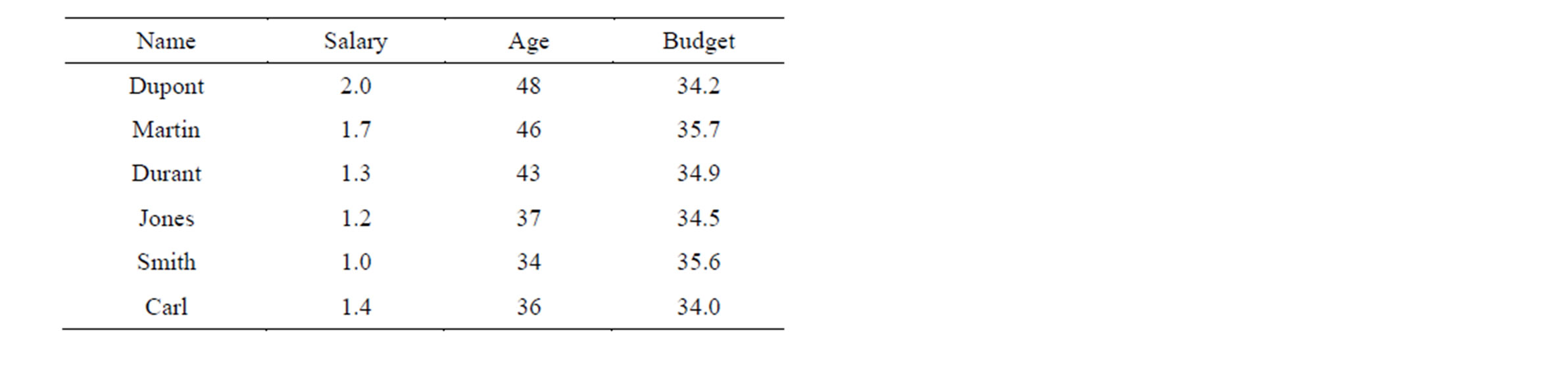
Table 1. Table of employees.
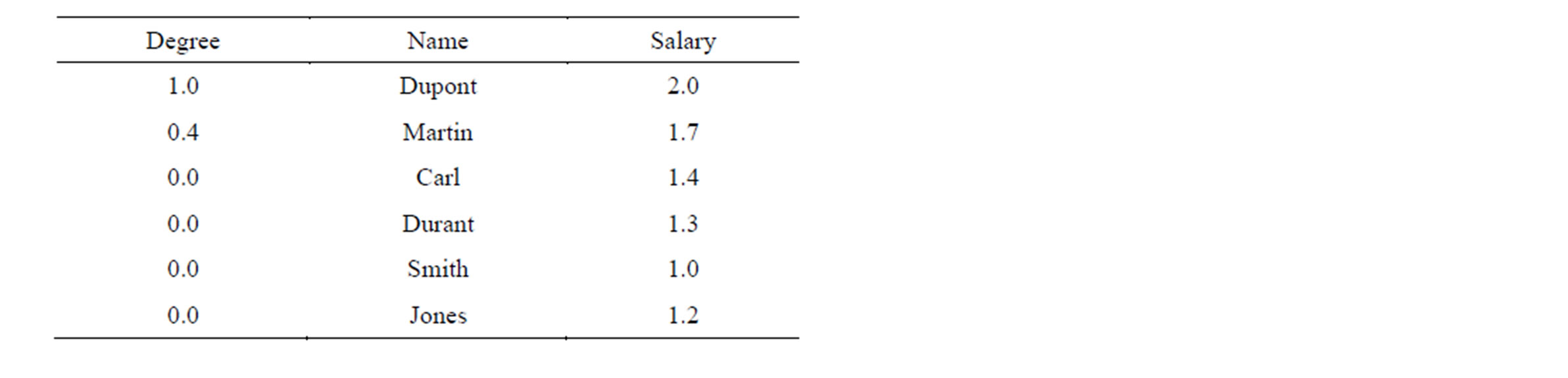
Table 2. Answers to a flexible query.

Table 3. Empty Answer Problem (EAP).

Table 4. Overabundant Answer Problem (OAP).
no means of selecting the best answers. This is the situation referred as OAP.
3. A Unified Solution to EAP and OAP
This section defines the concepts of semantic proximity, predicate transformation and query modification; afterwards, a unified solution to EAP and OAP is proposed.
3.1. Semantic Proximity
Let U be a subset of the real line. A proximity relation is a reflexive and symmetric fuzzy relation E on U, i.e., mE(x, x) = 1 and mE(x, y) = mE(y, x), for x, yÎU. The value mE(x, y) is the degree of approximated equality of x and y.
A relative proximity relation is defined in terms of the ratio x/y, that is, mE(x, y) = mR(x/y), where R is a tolerance parameter such that:
• mR(x) = 0 if x £ 0 (to avoid zero-division, assuming that approximately equal values have same sign);
• mR(1) = 1 (to guarantee the reflexivity property, that is, mE(x, x) = mR(x/x) = 1); and
• mR(x) = mR(1/x) (to guarantee the symmetric property, that is, mE(x, 1) = mE(1, x)).
Furthermore, to ensure symmetry, the support of R must be of the form , with 0 £ e < 1.
, with 0 £ e < 1.
In fact, R is a fuzzy predicate expressing “closer to 1”. Based on it, we can define the relation mN(x, y), called negligibility relation, that expresses “x is negligible (or insignificant) relatively to y” as follows:
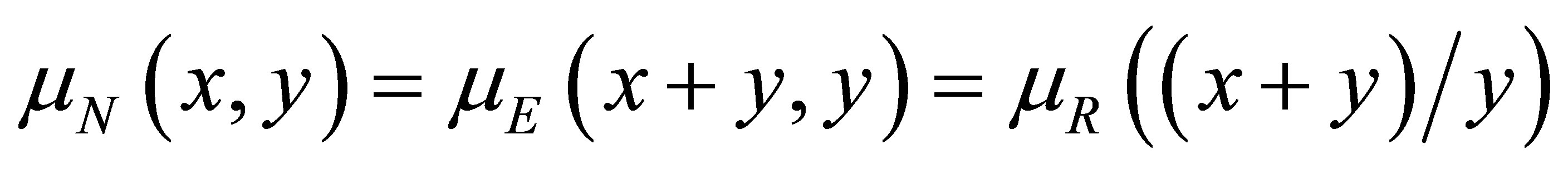
In order to guarantee all the properties of these three relations, it was proved in [13] that, using the interval
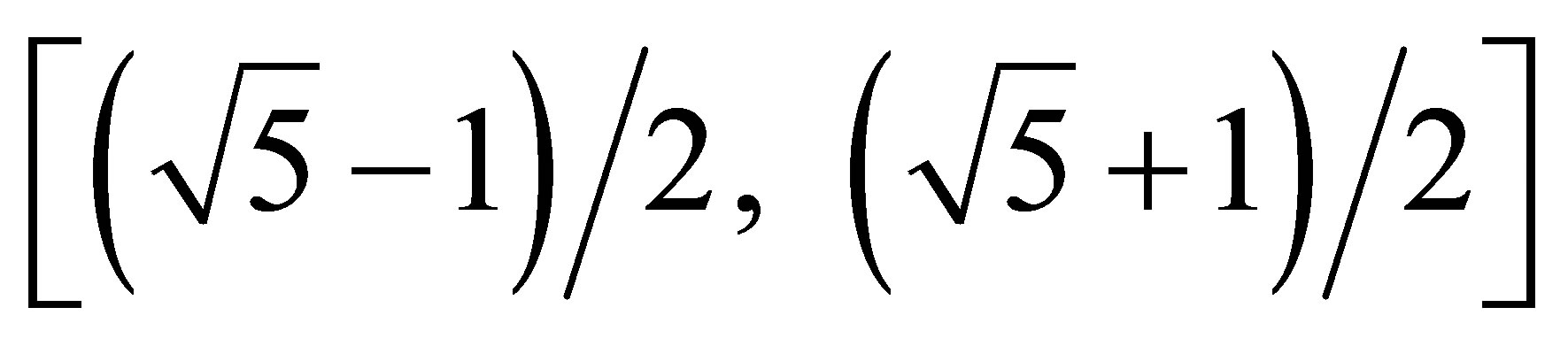 as support of R, all α-cut of R in the form
as support of R, all α-cut of R in the form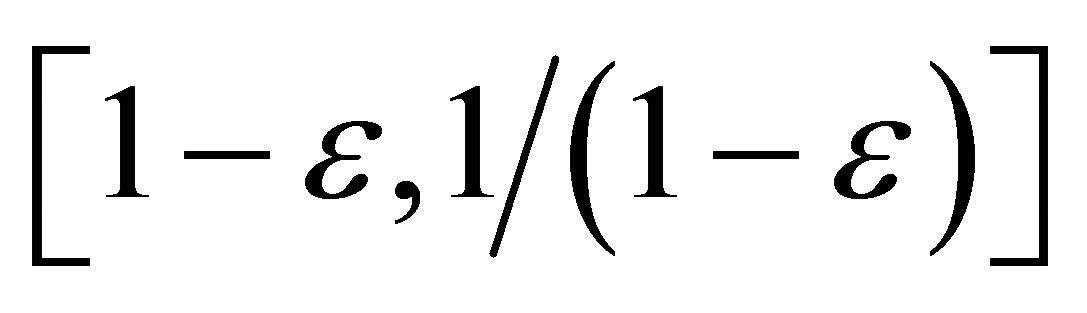 must have
must have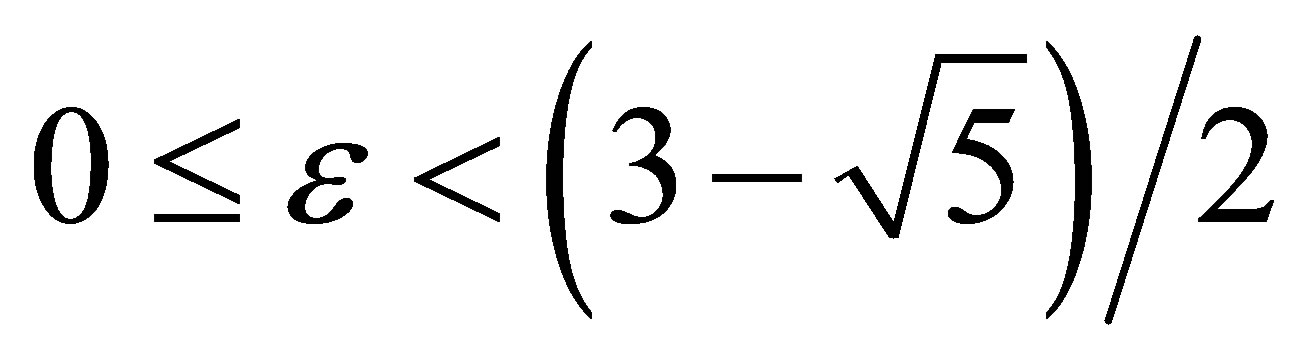 , that is, e Î [0, 0.38].
, that is, e Î [0, 0.38].
Therefore, if a transformation must preserve semantic proximity, the maximal relaxation allowed for a fuzzy membership function used as condition in a query being relaxed is restricted to the tolerance value e = 0.38.
3.2. Predicate Transformations
A predicate transformation T transforms a predicate P in a related variant T(P). When semantic proximity is taken into account, the resulting variant is semantically near to P, but it can be less restrictive or more restrictive than P.
Let P be a predicate, characterized by a trapezoidal membership function mP(x) = tmf(x, a, b, d). The predicate transformations proposed in literature [12,13,15] are mainly based on the following simple principles:
• If P leads to an empty answer set, clearly, all available data is out of supp(mP) = [b - d, c + d]. Therefore, to solve this problem, a relaxation transformation T must stretch the interval [b - d, c + d], so that supp(mP) Ì supp(mT(P)). This idea is shown in Figure 2(a).
• If P leads to an overabundant answer set, clearly, most part of the available data is in core(mP) = [b, c]. Therefore, to solve this problem, an intensification transformation T must shrink the interval [b, c], so that core(mT(P)) Ì core(mP). This idea is shown in Figure 2(b).
3.3. Query Modification Approaches
Let Q be a flexible query with vague condition C and let
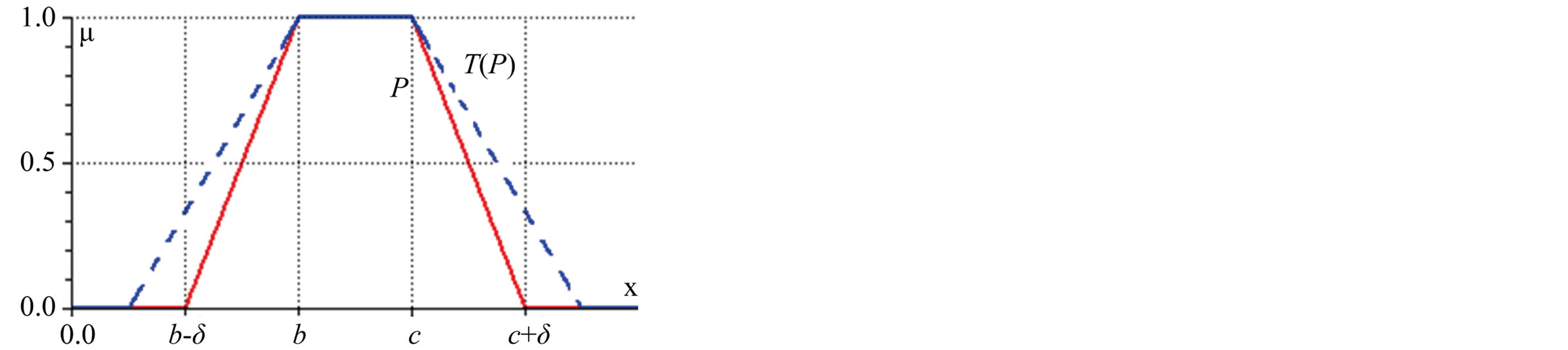 (a)
(a) (b)
(b)
Figure 2. Transformations: (a) stretch and (b) shrink.
T be a predicate transformation. There are two main approaches to obtain a new variant Q’ of Q, by applying T to predicates in C. In the local modification approach, T is applied only to some predicates in C; and in the global modification approach, T is applied to all predicates in C.
The local modification approach is appropriated when the cause of an empty answer to Q must be identified. In this case, a lattice of all possible variants of Q must be traversed (in a breadth-first search fashion) and, for each variant Q’ of Q, an answer set must be retrieved. Thus, if this answer set is not empty, the cause of the empty answer to Q can be explained by the modified predicates in the vague condition of the successful variant Q’. For example, a lattice for variants of a query Q with vague condition P1 Ù P2 Ù P3 is depicted in Figure 3. Supposing that the first non empty answer set is retrieved by the variant T(P1) Ù P2 Ù P3, then we can say that the cause of the empty answer to Q is P1.
A drawback of the local modification approach is that, in the worst case, it consumes exponential time. Therefore, in many practical applications, the cost of using the local query modification may be prohibitive.
Another drawback of local query modification is that the semantics of a variant Q’ may not match, as much as possible, the semantics of Q, because the predicates in Q are transformed in an arbitrary order (i.e., without taken into account the user’s preferences, which are unknown).
For example, consider a flexible query Q with a vague condition P1 Ú P2 Ú P3, that has an empty answer set (e.g., mPi(x) = 0, for all i and all available data x). Clearly, the intuitive semantics of disjunction is not exclusive. However, if a transformation is applied to relax only P1, and this is sufficient to retrieve a non empty answer set, then
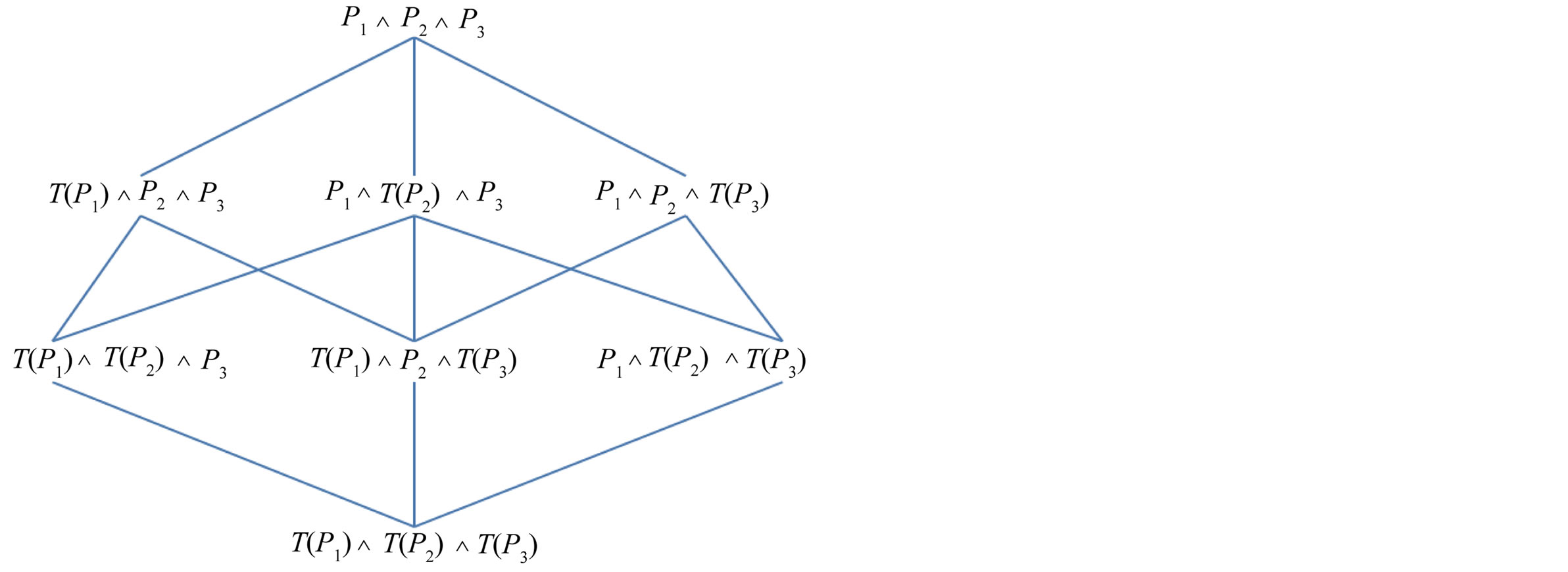
Figure 3. Lattice of variants of a query.
this answer set will contain only data satisfying P1 (i.e., the preference of P1, relatively to the other predicates in Q, is increased). On the other hand, if Q has an overabundant answer set (i.e., mPi(x) = 1, for all i and the most part of the available data x) and a transformation is applied to intensify only P1, then the resulting answer set will contain relatively few data completely satisfying P1 (i.e., the preference of P1, relatively to the other predicates in Q, is decreased). Similar problems can also occur for flexible queries with conjunctive conditions.
Therefore, since our aim is not to explain failing queries, the global modification approach will be adopted.
3.4. The Stretch & Shrink Transformation
Let mP(x) = tmf(x, b, c, δ) be a symmetric trapezoidal function, with support [b - d, c + d] and core [b, c], and let x be a value selected from an available dataset. It is known that if the all possible values of x are in the interval [-¥, b - d] or [c + d, +¥], then we have an EAP. Inversely, if all possible values of x are concentrated in the interval [b, c], we have an OAP. Thus, to solve both problems, we propose a transformation that, simultaneously, stretches the support and shrinks the core of mP.
More precisely, the stretch & shrink transformation of a symmetric trapezoidal function mP(x) = tmf(x, b, c, δ) is a symmetric triangular function S(mP(x)) = tmf(x, m, m, δ'), where 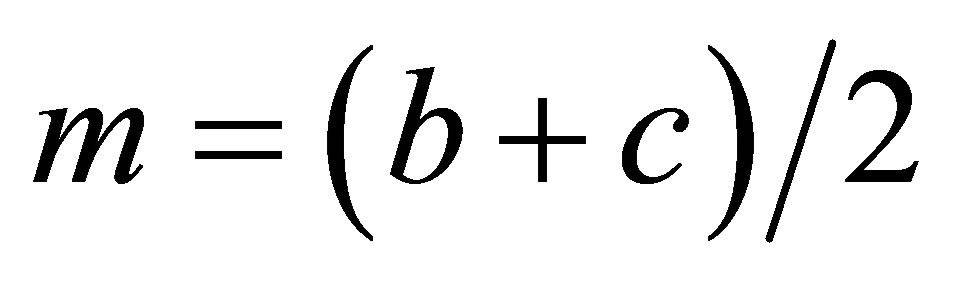 and
and , with negligible value e = 0.38. This idea is depicted in Figure 4.
, with negligible value e = 0.38. This idea is depicted in Figure 4.
As discussed in Subsection 3.1, the negligible value e ensures that S(mP(x)) is semantically not so far from mP(x). Indeed, when the stretch & shrink transformation is used to solve the OAP, the query with vague condition S(mP(x)) retrieves the same answer set retrieved by the query with vague condition mP(x), except due to the fact that the new answer set can be sorted in decreasing order of satisfaction degrees and, consequently, the user can select the best answers relatively to the prototype of S(mP(x)). On

Figure 4. Stretch & shrink transformation.
the other hand, when the stretch & shrink transformation is used to solve the EAP, the query with vague condition S(mP(x)) retrieves answers whose values are approx- imately equal to those in the boundaries of mP(x).
For example, considering the fuzzy predicates defined in Subsection 2.2, we have:
 (8)
(8)
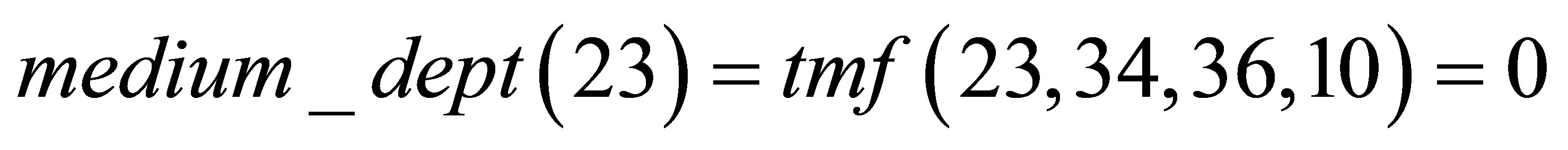 (9)
(9)
Now, by applying the transformation S to these predicates, we obtain:
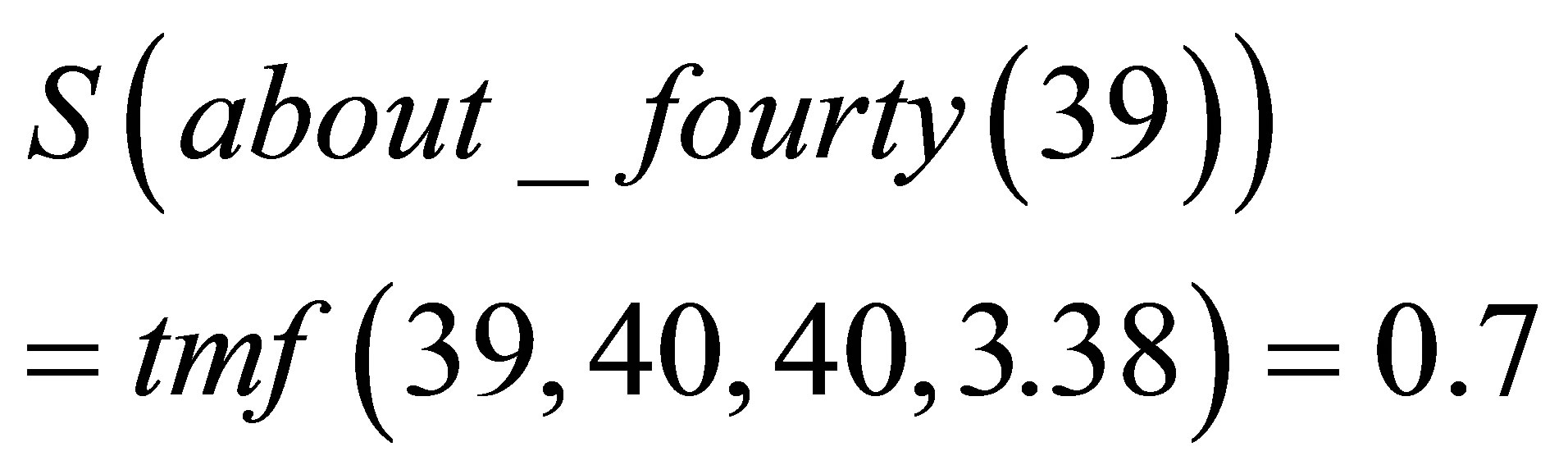 (10)
(10)
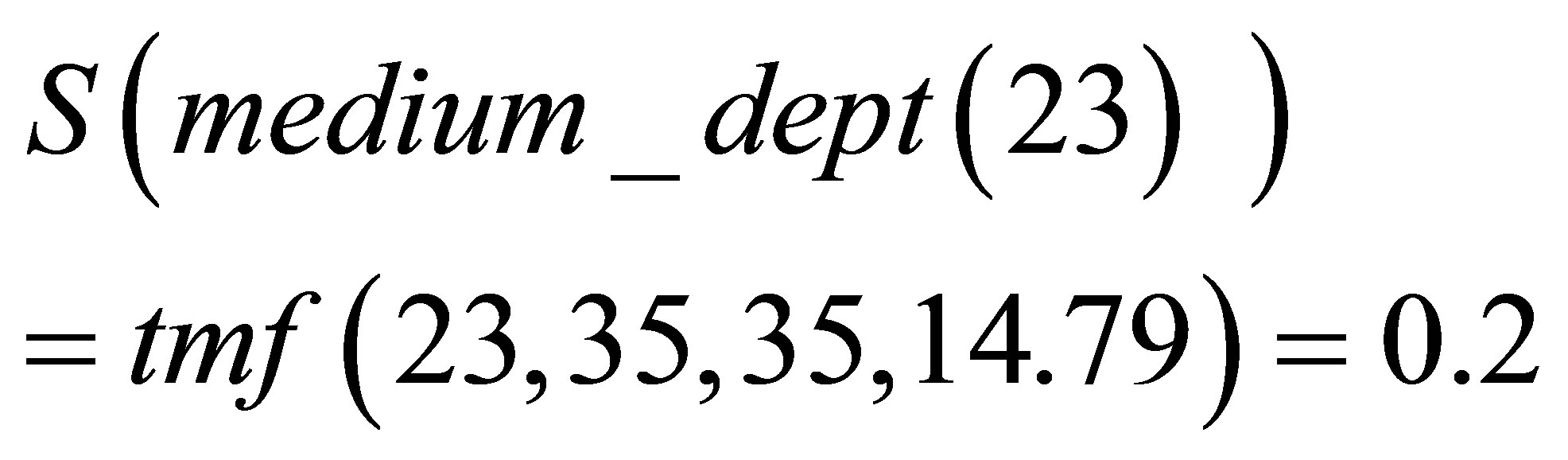 (11)
(11)
As can be observed, the transformation S relaxes the predicate medium_dept (solving an EAP) and intensifies the predicate about_fourty (solving an OAP).
It is worth to note that, the proposed transformation S always solves an OAP. However, the same does not occur with an EAP. If the available dataset does not contain any data satisfying S(mP(x)), this problem persists.
4. A Tool for Flexible Query Answering
To validate our proposal, a simple tool for flexible query answering was developed in SWI-Prolog [16], using the ODBC library to access the relational database MySQL [17]. This tool is composed of two applications:
• The Membership Function Designer is used to define predicates over attributes of a database table.
• The Flexible Query Executer is used to execute a flexible query submitted by a user or to automatically reformulate a flexible query that leads to an EAP or to an OAP (by applying the transformation stretch & shrink, proposed in the last section).
4.1. Membership Function Designer
The Membership Function Designer helps the user in the definition of the fuzzy predicates to be used as conditions in flexible queries. By using this application, the user can choose one of several predefined types of membership functions (e.g., Gaussian, bell and sigmoidal) and adjust its parameters, according to his intuition about the concept to be expressed by the predicate. After choosing the desired function, the user must select a table, and an attribute of it, to which the predicate will be associated. For example, Figure 5 shows the definition of the fuzzy predicate about_fourty, with argument age, for the table Employee.
The graphic for the defined function is plotted when the user clicks the button Plot. This helps him to validate its definition. When the user is finally satisfied, he can save the definition in the MySQL database, by clicking the button Save. After that, the new predicate can be used in flexible queries submitted to the associated database.
All information about fuzzy predicates defined by the user is maintained in a MySQL relational database table.
4.2. Flexible Query Executer
The Flexible Query Executer allows the user to formulate and to execute flexible queries in the connected database. When an EAP or an OAP occurs, this application also allows the user to submit a new related query, which is automatically reformulated by the system.
To formulate a flexible query, the user must specify the attributes to be selected, the table from which these attributes will be selected, a precise condition, a vague condition and a threshold (i.e., an a-cut).
To submit a flexible query, the user must to click the button Execute. As a result, the can see the corresponding query in standard SQL (automatically generated by the application) and the corresponding answer set (sorted in decreasing order of degrees). For example, Figure 6

Figure 5. Definition of a fuzzy predicate.

Figure 6. An example of EAP.
shows the result of the execution of a flexible query with vague condition medium_dept and about_fourty.
When the user faces an EAP (Figure 6), he can also click the button Stretch & Shrink to automatically submit a reformulated query to solve the problem (Figure 7).
Analogously, when the user faces an OAP (Figure 8), he can also click the button Stretch & Shrink to solve the problem, as can be seen in Figure 9.
4.3. Empirical Results
A series of experiments was performed to test the functionality of the developed tool.
In these experiments it was considered flexible queries with various types of vague conditions, such as conjunctive, disjunctive, negated and mixed conditions. It was also considered flexible queries with precise conditions and vague conditions.
In all the experiments, the results retrieved by the queries were compatible with those intuitively expected.
5. Conclusions
This paper proposes a unified solution to overabundant and empty answer problems, in the framework of flexible queries with fuzzy semantics.
The proposed solution consists in a predicate transformation, based on the concepts of semantic proximity and global query modification. This transformation, named stretch & shrink, is capable of relaxing or intensifying a query, in order to solve an empty or an overabundant answer problem.
To validate our proposal, a tool for flexible query answering was implemented. The experiments performed with this tool showed the effectiveness of the approach to the development of cooperative answering systems in the framework of flexible queries with fuzzy semantics.
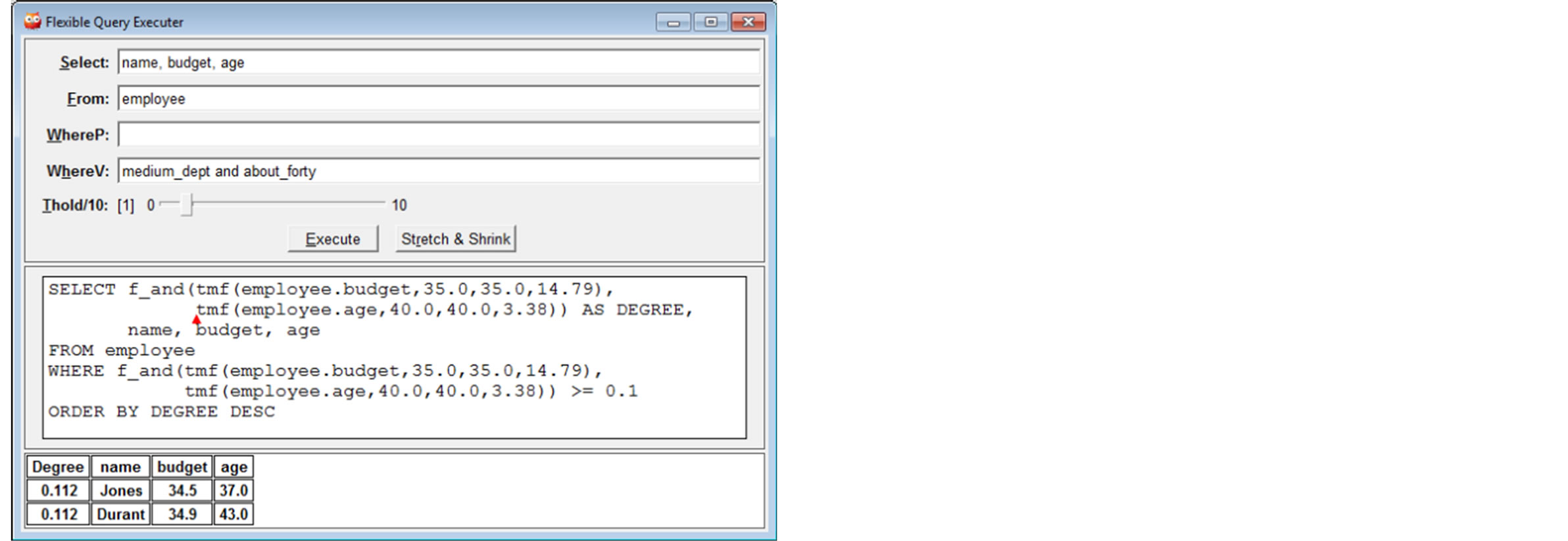
Figure 7. Solving EAP.
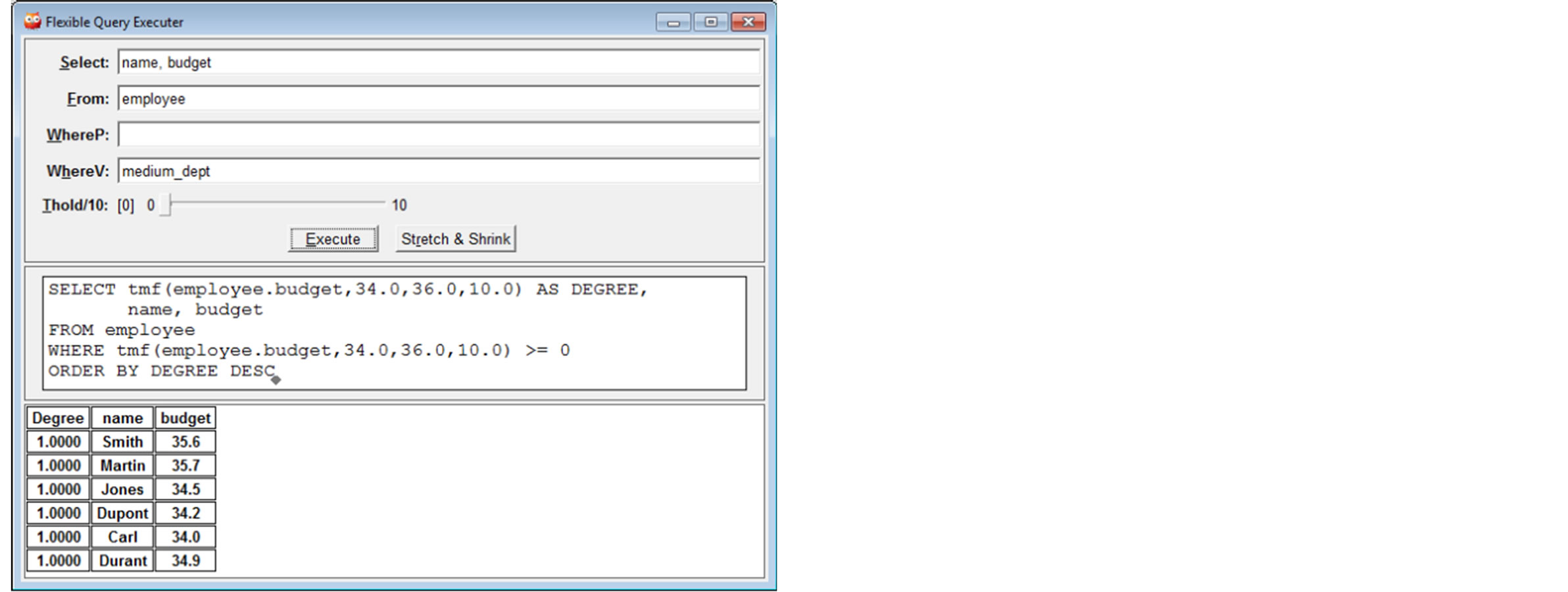
Figure 8. An example of OAP.
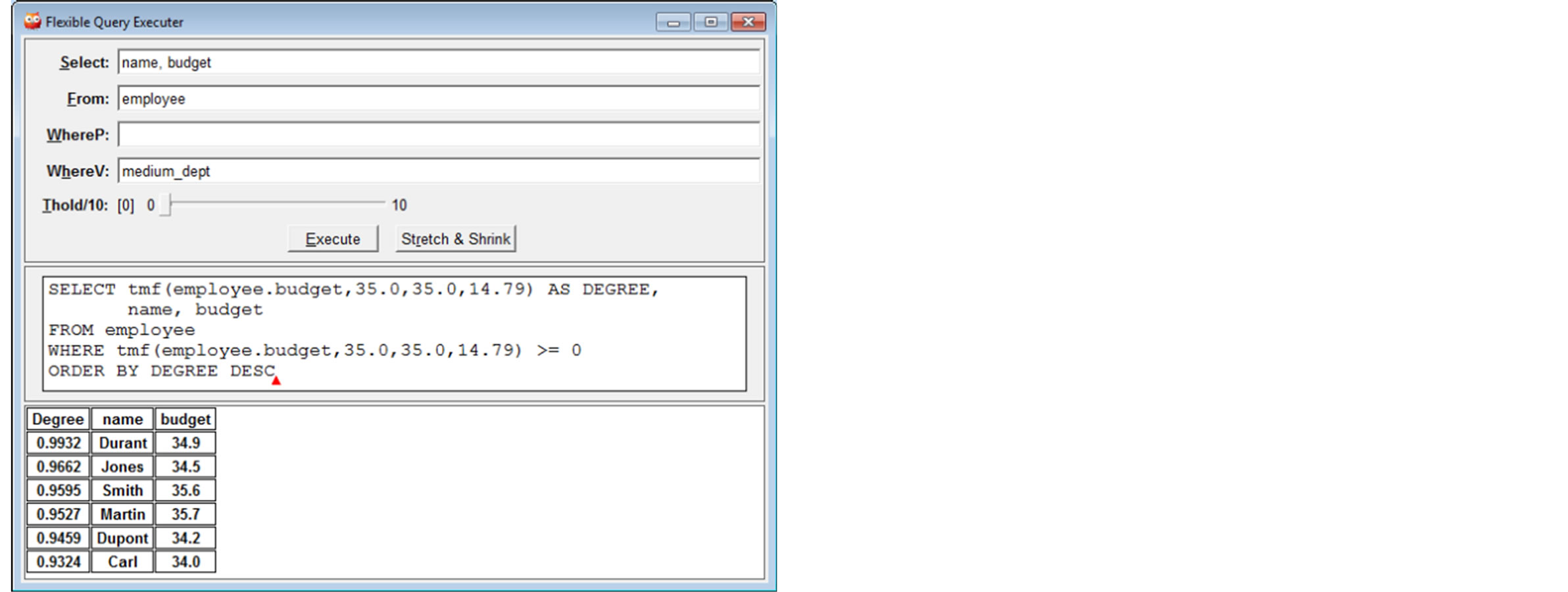
Figure 9. Solving OAP.
In future works, we intend to test the efficiency of the approach, when applied to large databases.
Acknowledgements
This research is supported by CNPq (Brazilian National Counsel of Technological and Scientific Development), under grant numbers 305484/2012-5 and 104200/2013-8.
REFERENCES
- S. Abiteboul, R. Hull and V. Vianu, “Foundation of Databases,” Addison-Wesley, Boston, 1994.
- A. G. Maguitman, “Intelligent Support for Knowledge Capture and Construction,” Ph.D. Dissertation, Indiana University, Indianapolis, 2004.
- D. H. Lee and M. H. Kim, “Accommodating Subjective Vagueness through a Fuzzy Extension to the Relational Data Model,” Information Systems, Vol. 18, No. 6, 1993, pp. 363-374. http://dx.doi.org/10.1016/0306-4379(93)90013-Q
- J. Galindo, A. Urrutia and M. Piattini, “Fuzzy Databases: Modeling, Design and Implementation,” Idea Group Publishing, Hershey, 2006.
- Z. M. Ma and L. Yan, “A Literature Overview of Fuzzy Database Models,” Journal of Information Science and Engineering, Vol. 24, No. 1, 2008, pp.189-202.
- L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- P. Bosc, A. Hadjali and O. Pivert, “Weakening of Fuzzy Relational Queries: An Absolute Proximity RelationBased Approach,” Mathware & Soft Computing, Vol. 14, No. 1, 2007, pp. 35-55.
- T. Gausterland, “Cooperative Answering through Controlled Query Relaxation,” IEEE Expert, Vol. 12, No. 5, 1997, pp. 48-59. http://dx.doi.org/10.1109/64.621228
- I. Muslea, “Machine Learning for Online Query Relaxation,” 10th International Conference of Knowledge and Discovery and Data Mining, Washington DC, 2004, pp. 246-255.
- T. Andreasen and O. Pivert, “On the Weakening of Fuzzy Relational Queries,” First 8th International Symposium on Methods for Intelligence System, Charlote, October 1994, pp. 144-153.
- P. Bosc, A. Hadjali and O. Pivert, “About Overabundant Answers to Flexible Queries,” Proceedings of the 11th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU’06), Paris, 2-7 July 2006, pp. 2221-2228.
- P. Bosc, A. Hadjali and O. Pivert, “Empty versus Overabundant Answers to Flexible Relational Queries,” Fuzzy Sets and Systems, Vol. 159, No. 12, 2008, pp. 1450-1467. http://dx.doi.org/10.1016/j.fss.2008.01.007
- A. Hadj Ali, D. Dubois and H. Prade, “Qualitative Reasoning Based on Fuzzy Relative Orders of Magnitude,” IEEE Transactions on Fuzzy Systems, Vol. 11, No. 1, 2003, pp. 9-23. http://dx.doi.org/10.1109/TFUZZ.2002.806313
- L. Wang, “A Course in Fuzzy Systems and Control,” Prentice-Hall, Upper Saddle River, 1997.
- E. E. Kerre and M. de Cock, “Linguistic Modifiers: An Overview,” In: G. Chen, M. Ying and K.-Y. Cai, Eds., Fuzzy Logic and Soft Computing, Vol. 9, Kluwer Academic Publishers, Norwell, 1999, pp. 69-85.
- I. Bratko, “Prolog Programming for Artificial Intelligence,” 4th Edition, Pearson, London, 2011.
- Oracle, “MySQL 5.6 Reference Manual.” http://dev.mysql.com/doc/refman

