International Journal of Geosciences
Vol.06 No.10(2015), Article ID:60662,12 pages
10.4236/ijg.2015.610088
Characterization of Source Parameters and Some Empirical Relations between Them for Kachchh Region, Gujarat, India: Implication of January 26, 2001 Bhuj Earthquake and Its Aftershock Sequence
Parul C. Trivedi1*, Imtiyaz A. Parvez2
1India Meteorological Department, Ahmedabad, India
2CSIR Fourth Paradigm Institute (Formerly C-MMACS), Bangalore, India
Email: *pctrivedi123@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 August 2015; accepted 24 October 2015; published 28 October 2015
ABSTRACT
Study of source parameters of small to moderate and large earthquakes is important to understand the differences and similarities between dynamic ruptures of different earthquakes and clarifying the scaling relations. In the present study, we have characterized source parameters and presented new and revised empirical relationships between various source parameters for Kachchh region of Gujarat, India to facilitate to draw first-order conclusions regarding the trends in the region. We have studied total 202 aftershocks of shallow-focus (hypo central depth less than 40 km) and moderate magnitude recorded over the Kachchh region during January 2001 to December 2012 by different seismological observatories of India Meteorological Department. We have adopted the spectral technique for source parameter estimation, where S-wave displacement spectra are considered and applied Fast Fourier Transform (FFT) to compute displacement spectra. We have followed the Brune’s source model for our estimation and the estimated values of source parameters show close approximation to the global values. While derived empirical relations between different source parameters, they demonstrate direct or inverse proportion to linear or power scale. Interrelation between seismic moment, rupture parameters, corner frequency and radiated seismic energy can be summarized as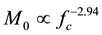 ,
, 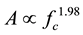 ,
,  and ER µ M0 and ER µ Mw for our analysis. Stress drop distribution over the Kachchh region is very scattered and due to its peculiar behavior, it is difficult to derive its empirical relation with other source parameters. Sufficient accuracy on measuring source parameters like corner frequency stress drop, rupture dimensions, radiated seismic energy etc. helps to understand earthquake processes in the region. This is the first ever attempt to establish empirical relation between different source parameters for Kachchh region for longer aftershock sequence and they are useful to assess future earthquake potential over the region.
and ER µ M0 and ER µ Mw for our analysis. Stress drop distribution over the Kachchh region is very scattered and due to its peculiar behavior, it is difficult to derive its empirical relation with other source parameters. Sufficient accuracy on measuring source parameters like corner frequency stress drop, rupture dimensions, radiated seismic energy etc. helps to understand earthquake processes in the region. This is the first ever attempt to establish empirical relation between different source parameters for Kachchh region for longer aftershock sequence and they are useful to assess future earthquake potential over the region.
Keywords:
Source Parameters, Bhuj Earthquake, Aftershock Sequence, Empirical Relations

1. Introduction
Hazard analysis involved with seismic activity is based on the estimation of the future earthquake potential in a given region. The future earthquake potential of a fault is evaluated from estimates of fault rupture parameters which are directly related to earthquake magnitude. Source parameters of small to moderate and large earthquakes are important for understanding the differences and similarities between dynamic ruptures of small and large earthquakes and clarifying the scaling relations. However, it is often difficult to accurately determine source parameters of small earthquakes because relatively high-frequency seismic waves excited by small earthquakes are easily scattered and attenuated along the path. Many researchers have published their studies on source parameters for different regions of the world [1] -[4] . The purpose of this study is to characterize the source parameters and to present new and revised empirical relationships between various source parameters for Kachchh region of Gujarat province of India. In this study, the source parameters discussed most often are seismic moment M0, moment magnitude Mw, stress drop Δσ, corner frequency fc and rupture area A. We have interrelated some of these parameters on the basis of assumptions of similarity and scaling and spectral source theories.
2. Data and Methodology
2.1. Data
For the present study, we have used total 202 aftershocks of magnitude Mw ≥ 4.0 (except some events of 3.5 < Mw < 4.0) for the aftershock sequence of January 26, 2001 Bhuj earthquake. The data include shallow-focus (hypo central depth less than 40 km), continental intraplate earthquakes from January 26, 2001 to December 31, 2012 recorded by different seismological observatories of India Meteorological Department (IMD). The epicentral locations of all earthquakes under the study are shown in Figure 1. For each earthquake in the data used, we have estimated earthquake source parameters including seismic moment, moment magnitude, rupture radius and rupture area, stress drop and radiated seismic energy which describe the source dynamics in the best possible way. Data are categorized the type of measurement and the most accurate value is selected for further analysis. To develop empirical relations among various source parameters for Kachchh region, from the larger database, some of the aftershocks data are evaluated but excluded from further study because of poor-quality of data.
2.2. Method
There are two approaches to describe source parameters. The simplified approach describes the seismic source by limited number of parameters such as the origin time and location, initial rupture, magnitude, intensity or acceleration of measured ground shaking and sometimes fault plane solution. These are easily obtainable parameters and provide quick information to the public and concern authorities. Nevertheless, they are fundamental for different research, they are not sufficient to describe the true nature and geometry or the energy release by the source. The second approach deals with the detailed analysis of a given event i.e., analyzing near and far-field waveforms and spectra of seismic waves. It provides important information on energy distribution at the source of the seismic event in the frequency domain. We have adopted the second approach i.e. the spectral technique for source parameter estimation and followed the Brune’s [5] source model for our estimation, where S-wave displacement spectra are considered. The spectral analysis for local and regional events is performed in single
Figure 1. Epicentral locations of seismic events (Mw ≥ 3.5) for the present study.
trace mode from the three-component seismogram. An example of the three-component seismogram recorded at station Bhuj for moderate earthquake of magnitude Mw ~ 5.5 is shown in Figure 2. The onset of S-wave arrival time was estimated from the displacement spectra recorded at a given station and then they were band pass filtered between 0.1 and 20.0 Hz. From the filtered waveform, a time window of 10 second duration was selected for all the analysis undertaken in this study. We have applied Fast Fourier Transform (FFT) to compute displacement spectrum. The spectral analysis performed here is based on the Brune’s [5] model and assumptions about the geometrical spreading and inelastic attenuation. Out of 202 moderate magnitude aftershocks under this study, displacement spectra for some selected aftershocks recorded by Bhuj seismological observatory are displayed in Figure 3.
2.3. Basic Formulations
Theoretical displacement spectrum d(f) according to Brune [5] can be written as,
 (1)
(1)
where, M0 is the seismic moment (N.m),  is defined as radiation pattern function and taken as 0.55 (average value of different fault geometry), f is frequency (Hz), fc is corner frequency (Hz), ρ is density at the source and taken 2700 kg/m3, Vp,s is seismic-wave velocity of the corresponding phase and they are 6.2 km/sec for P-wave and 3.6 km/sec for S-wave. In equation (1), the term G (r,h) represents geometrical spreading, for S- wave, it has been considered to depend on distance and depth. For distance r and depth h, geometrical spreading G(r,h) = 1/r (for r < 100 km) and G(r,h) = 1/(100 × r)1/2 [6] . In the present study, all earthquakes are of shallow depth i.e. depth less than 40 km, thus we have considered G(r,h) = 1/r throughout this study. According to the Brune’s [5] source model, D(f) is the diminution function due to inelastic attenuation and can be given as follow,
is defined as radiation pattern function and taken as 0.55 (average value of different fault geometry), f is frequency (Hz), fc is corner frequency (Hz), ρ is density at the source and taken 2700 kg/m3, Vp,s is seismic-wave velocity of the corresponding phase and they are 6.2 km/sec for P-wave and 3.6 km/sec for S-wave. In equation (1), the term G (r,h) represents geometrical spreading, for S- wave, it has been considered to depend on distance and depth. For distance r and depth h, geometrical spreading G(r,h) = 1/r (for r < 100 km) and G(r,h) = 1/(100 × r)1/2 [6] . In the present study, all earthquakes are of shallow depth i.e. depth less than 40 km, thus we have considered G(r,h) = 1/r throughout this study. According to the Brune’s [5] source model, D(f) is the diminution function due to inelastic attenuation and can be given as follow,
 (2)
(2)
Figure 2. Three-component seismogram recorded at Bhuj for the event January 28, 2001(Mw 5.5).
where, k accounts for kappa, the near-surface high frequency attenuation with the constant kappa having a value of 0.025 for Kachchh region [7] , t is taken as travel time and Q(f) is frequency dependent inelastic attenuation. Furthermore, taking the attenuation factor into account and following the Andrews [8] , the amplitude spectrum in frequency domain is a product of a source and site spectral function and a propagation path term. Thus, the amplitude spectrum of the ith event recorded at jth station at a distance of r and for frequency f can be written as [9] - [11] ,
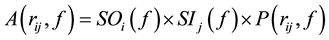 (3)
(3)
where, SOi and SIj are source and site spectral function respectively and P(rij, f) is the propagation path term which can be expressed as,
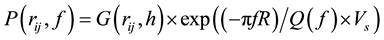 (4)
(4)
The term G(rij,h) is geometrical spreading and similar to G(r, h) of Equation (1) as discussed earlier and Vs is assumed to be 3.6 km/sec based on a velocity model of the Kachchh region [12] [13] . We have considered a known Q(f) relation based on the result of the coda-Qc study of the Kachchh region by Mandal et al. [14] and expressed by Equation (5),
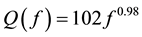 (5)
(5)
In the coda Qc study, Mandal et al. [14] have used Aki and Chouet’s [15] technique, where the coda waves were assumed to be composed of the backscattered S-waves. Thus, the Qc estimates obtained using Aki and Chouet’s [15] technique can be considered to be very close to the estimates of Q(f) [16] . Mandal et al. [17] also experimented the effect of Q on the site response estimates considering three available frequency dependent relations, i.e., 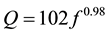 (from local coda waves by Mandal et al. [14] ),
(from local coda waves by Mandal et al. [14] ), 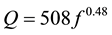 (from regional Lg waves by Singh et al. [18] ) and
(from regional Lg waves by Singh et al. [18] ) and 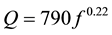 (obtained by Bodin and Horton, [19] from the study of ground- motion prediction) and found no significant difference in the shape and amplitude of the site response estimates using the aforementioned three Q values.
(obtained by Bodin and Horton, [19] from the study of ground- motion prediction) and found no significant difference in the shape and amplitude of the site response estimates using the aforementioned three Q values.
Figure 3. Displacement spectra for some events recorded at station Bhuj.
In a homogeneous half-space, M0 can be determined from the spectra of seismic waves observed at the Earth’s surface by using the relationship given by Brune [5] ,

where, R is epicentral distance (km) and Ω0 is long period amplitude level (m-sec).
From the spectral parameters, other parameters like moment magnitude, source radius, stress drop and radiated seismic energy are derived using Equation (3) to Equation (8) as follows,
Moment magnitude (Hanks and Kanamori, [20] ),

Rupture radius and area,


where, r is rupture radius (km), A is rupture area (sq∙km) and fc is corner frequency (Hz).
Stress drop (Kellis-Borok, [22] ),

Radiated seismic energy (Richter, [23] ),

3. Results and Discussion
The results of our analysis are summarized in Table 1 and displayed by graphs from Figures 4-7. Errors associated in estimation of source parameters can be represented by standard deviation and mean values. The mean and standard deviation values in estimation of seismic moment can be given below [24] ,

Figure 4. Relation between corner frequency and other source parameters.
Table 1. Estimated source parameters for Kachchh region.
Figure 5. Relation between moment magnitude, seismic moment and rupture area.

Figure 6. Relations between radiated seismic energy and other parameters.
Mean of seismic moment,

Standard deviation of seismic moment,

We have followed the same procedure as mentioned above to calculate mean and standard deviation in corner frequency and rupture radius. Stress drop values are highly deviate from the mean hence we have derived percentage error for stress drop which can be defined as,
Figure 7. Distribution of stress drop over Kachchh region.

Mean values of corner frequency, seismic moment, rupture radius and stress drop are 2.886 Hz, 2.3 × 1016 N.m, 0.597 km and 200.8 bar respectively whereas standard deviation in estimation of corner frequency, seismic moment and rupture radius are 1.296 Hz, 0.67 N∙m and 0.361 km respectively. As discussed, we have calculated an average % error in the estimation of stress drop as stress drop values are discrete and they found to be 3%.
In the process, we have further derived empirical relations between the estimated source parameters, which are described individually in following subsequence. The empirical relations between source parameters we have derived in the present study can be grouped in three different categories, i.e., empirical relations for seismic moment, empirical relations for rupture parameters and empirical relations for radiated seismic energy.
3.1. Empirical Relations for Seismic Moment
Seismic moment relations with corner frequency and rupture area are shown in Figure 4(a) and Figure 4(b) respectively. According to Hanks and Kanamori [20] and Hanks et al. [25] , seismic moment is related to rupture area. An average displacement after the rupture can be given as 









3.2. Empirical Relation for Rupture Area
Rupture area to corner frequency relation is shown in Figure 5. According to Figure 5, rupture area inversely proportionate to the square of corner frequency, i.e. 
3.3. Empirical Relations for Radiated Seismic Energy
Figure 6(a) and Figure 6(b) represents radiated seismic energy to seismic moment and moment magnitude relation respectively. Early attempts to quantify the size of earthquakes were based on estimating the intensity of damage in earthquakes. With the advent of broadband seismometers, we can now directly integrate seismic velocity data to determine radiated seismic energy [32] . Additionally, radiated seismic energy is not only a measure of the size of the earthquake but also a macroscopic parameter that can be used to obtain insights into the rupture mechanisms of earthquakes. For the present work, we have found radiated seismic energy ranging from 2.2 × 1010 J to 2.0 × 1013 J for Kachchh region for the magnitude range from 3.5 < Mw < 5.7. It has been observed that each earthquake has unique characteristics even if they are of same category and of same region. The radiated seismic energy is an important parameter that represents the dynamic characteristic of the earthquake mechanics and helps to understand differences between earthquakes. From Figure 6(a) and Figure 6(b), it can be observed that radiated seismic energy follows linear relation to M0 and Mw. Choy and Boatwright [33] analyzed 394 shallow-focus earthquakes over the globe and obtained the relation between radiated seismic energy and moment




3.4. Stress Drop Distribution
Stress drop results are listed in the Table 1 and estimated stress drop values ranges from 68.4 bar to 299.8 bar for January 2001 Bhuj aftershock sequence, which are in accordance with global values for intraplate earthquakes. Due to peculiar behavior of stress drop over the region, it is difficult to establish the relation between stress drop and other source parameters; therefore we have presented here its spatial distribution over the Kachchh region in Figure 7. Stress drop changes on the fault are one of the most significant indicators specifying dynamic behavior of earthquake ruptures [5] . The relationship between stress drop, apparent stress and earthquake moment remains a controversial topic due to the difficulty in correcting propagation effects [36] .
Earthquakes with higher stress drops will have more intense ground motions. Large earthquake populations reveal strong variations in stress drop but little in the way of systematic behavior or dependence on seismic moment [37] . Because static stress drop measurements depend on the corner frequency cubed, the small uncertainties in corner frequency, map into large uncertainties in the stress drop and it is often unclear how much of this variability is due to measurement error rather than variability in source properties [38] [39] . In this study, as stated earlier, we have found no systematic relationship of stress drop with seismic moment and other source parameters; however, we have found several anomalous events with very high stress drops than average values. The energetic events could have high stress drop or high rupture velocity, which suggest that there might be a population of earthquakes that have particularly intense strong ground motion for their size. Stress drop distribution over Kachchh region is less discussed so far and we have observed that high stress drop values (>200 bar) are found away from the fault in the most of cases whereas low and moderate stress drop values (<200 bar) are observed for events at the fault or near the fault. Not a single event located at the fault which exhibits high stress drop value except one at North Wagad fault in this study.
Faultwise stress drop distribution can be described as follow:
Events located near Gora Dungar fault show lower stress drop values compared to other faults of Kachchh region.
Gedi fault having moderate stress drop events.
Western part of widely known North Wagad fault exhibits moderate stress drop values at the same time eastern part exhibits that of higher values. Northwest of South Wagad fault can be characterized by higher stress drop values.
Only few events with high stress drop values are observed at Kachchh Mainland fault (KMF) and that is again at extreme eastern end of KMF. While North of KMF and South of KMF are confined with high stress drop events.
This difference in stress drop from one fault to another can be explained with fault geometry, frictional strength of faults and crustal brittleness. There are several possible reasons for variation in stress drop over the Kachchh region. The inferred high heat flow for Kachchh region can be attributed to the presence of mafic instructive at lower crustal depths in the region [40] , which leads to higher deep crustal temperatures. This cold mafic crust provides enough brittleness to generate large earthquake with high stress drop in the lower crust. Another possibility is that the stress drop varies due to variations of pore fluid pressure [41] .
4. Conclusions
In the present study, the source parameters of crustal earthquake for moderate magnitude occurred in Kachchh seismic zone were estimated using Brune’s theory by estimating corner frequency and the low frequency asymptote from the spectral technique. The estimated source parameters are summarized in Table 1 and are in accordance with the global values of intraplate earthquakes. The empirical relationships between the source parameters are also proposed. On the basis of analysis carried out during our study, we have come to the following conclusions:
Seismic moment and hence the moment magnitude are inversely proportional to corner frequency for Kachchh region and in accordance with Gutenberg-Richter relation [34] .
Seismic moment to rupture area relation from our analysis is identical to the average relation suggested by Abe [30] .
Estimated stress drop values are found to be very scattered. Stress-drop behavior also depends on the tectonic characteristics of the region. Moreover, the properties of the earth’s crust change from one to another location. Thus, stress drop observations cannot extrapolate from high stress drop regions to moderate or low stress drop regions and vice versa even for earthquakes of similar magnitudes. Lower stress drop values estimated for the events are recorded near the fault while higher stress drop values are found for events recorded far away from the fault irrespective of magnitude.
An important outcome of our study is that the full range of magnitude we have considered is having power scale with rupture size. Radiated seismic energy ranges from 1010 J to 1013 J and exhibits linear relation with M0 and Mw.
Sufficient accuracy on measuring source parameters like stress drop, rupture dimensions and radiated seismic energy helps to understand earthquake source processes. It has considerable implications for studies of earthquake rupture physics and seismic hazards for large earthquake. By applying proper conditions and considering uncertainties in locations, we can increase our ability to estimate ground motion from large earthquakes. We conclude that even though, the quantitative prediction of earthquake initiation is an extremely complicated task, by integrating knowledge of the propagation of seismic waves and strength of seismic shaking, the state of stress in the crust and detailed slip inversions combining geodetic methods, earthquake mitigation can be achieved and it is the best possible practical approach to save the loss of lives and properties.
Acknowledgements
The authors are grateful to India Meteorological Department for providing valuable data and permission to publish this work. We would like to extend our sincere thanks to Scientist-In-Charge, CSIR Fourth Paradigm Institute (formerly C-MMACS) for providing the facilities. We are thankful to Mr. Sandeep Agarwal for his help to solve Seisan related issues.
Cite this paper
Parul C.Trivedi,Imtiyaz A.Parvez, (2015) Characterization of Source Parameters and Some Empirical Relations between Them for Kachchh Region, Gujarat, India: Implication of January 26, 2001 Bhuj Earthquake and Its Aftershock Sequence. International Journal of Geosciences,06,1127-1139. doi: 10.4236/ijg.2015.610088
References
- 1. Darragh, R.B. and Bolt, B.A. (1987) A Comment on the Statistical Regression Relation between Earthquake Magnitude and Fault Rupture Length. Bulletin of the Seismological Society of America, 77, 1479-1484.
- 2. Kanamori, H. and Anderson, D.L. (1975) Theoretical Basis of Some Empirical Relations in Seismology. Bulletin of the Seismological Society of America, 65, 1073-1096.
- 3. Purcaru, G. and Berckhemer, H. (1982) Quantitative Relations of Seismic Source Parameters and a Classification of Earthquakes. In: Duda, S.J. and Aki, Eds., Quantification of Earthquakes, Tectonophysics, 84, 57-128. http://dx.doi.org/10.1016/0040-1951(82)90154-8
- 4. Singh, S.K., Bazan, E. and Esteva, L. (1980) Expected Earthquake Magnitude from a Fault. Bulletin of the Seismological Society of America, 70, 903-914.
- 5. Brune, J. (1970) Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes. Journal of Geophysical Research, 75, 4997-5009. http://dx.doi.org/10.1029/JB075i026p04997
- 6. Herrmann, R.B. and Kijko, A. (1983) Modelling Some Empirical Vertical Component Kg Relations. Bulletin of the Seismological Society of America, 73, 157-171.
- 7. Singh, S.K., Apsel, R.J., Fried, J. and Brune, J.N. (1982) Spectral Attenuation of SH-Waves along the Imperial Fault. Bulletin of the Seismological Society of America, 72, 2003-2016.
- 8. Andrews, D.J. (1986) Objective Determination of Source Parameters and Similarity of Earthquakes of Different Size, Earthquake Source Mechanics. American Geophysical Union, Washington DC, 259-268.
- 9. Lermo, J. and Chavez-Garcia, F.J. (1993) Site Effect Evaluation Using Spectral Ratios with Only One Station. Bulletin of the Seismological Society of America, 83, 1574-1594.
- 10. Nath, S.K., Sengupta, P. and Kayal, J.R. (2002) Determination of Site Response at Garhwal Himalaya from the Aftershock Sequence of 1999 Chamoli Earthquake. Bulletin of the Seismological Society of America, 92, 1071-1081. http://dx.doi.org/10.1785/0120000246
- 11. Nath, S.K., Biswas, N.N., Dravinski, M. and Papageorgiou, A. (2002) Determination of S-Wave Site Response in Anchorage, Alaska in the 1 - 9 Hz Frequency Band. Pure and Applied Geophysics, 159, 2673-2698. http://dx.doi.org/10.1007/s00024-002-8753-4
- 12. Mandal, P. (2007) Sediment Thicknesses and Qs vs. Qp Relations in the Kachchh Rift Basin, Gujarat, India Using Sp Converted Phases. Pure and Applied Geophysics, 164, 135-160.
http://dx.doi.org/10.1007/s00024-006-0158-3 - 13. Mandal, P. and Pujol, J. (2006) Seismic Imaging of the Aftershock Zone of the 2001 Mw 7.7 Bhuj Earthquake, India. Geophysical Research Letters, 33, Article ID: L05309.
- 14. Mandal, P., Jainendra, S., Joshi, S., Kumar, S., Bhunia, R. and Rastogi, B.K. (2004) Low Coda-Qc in the Epicentral Region of the 2001 Bhuj Earthquake of Mw 7.7. Pure and Applied Geophysics, 161, 1635-1654. http://dx.doi.org/10.1007/s00024-004-2525-2
- 15. Aki, K. and Chouet, B. (1975) Origin of Coda Waves: Source, Attenuation and Scattering Effects. Journal of Geophysical Research, 80, 3322-3342. http://dx.doi.org/10.1029/jb080i023p03322
- 16. Mandal, P., Chadha, R.K., Satyamurty, C., Raju, I.P. and Kumar, N. (2005) Estimation of Site Response in Kachchh, Gujarat, India, Region Using H = V Spectral Ratios of Aftershocks of the 2001 Mw 7.7 Bhuj Earthquake. Pure and Applied Geophysics, 162, 2479-2504. http://dx.doi.org/10.1007/s00024-005-2784-6
- 17. Mandal, P., Dutta, U. and Chadha, R.K. (2008) Estimation of Site Response in the Kachchh Seismic Zone, Gujarat, India. Bulletin of the Seismological Society of America, 98, 2559-2566.
http://dx.doi.org/10.1785/0120070309 - 18. Singh, S.K., Pacheco, J.F., Bansal, B.K., Perez-Campos, X., Dattatrayam, R.S. and Suresh, G. (2004) A Source Study of the Bhuj, India, Earthquake of 26 January 2001 (Mw 7.6). Bulletin of the Seismological Society of America, 94, 1195-1206. http://dx.doi.org/10.1785/012003212
- 19. Bodin, P. and Horton, S. (2004) Source Parameters and Tectonic Implications of Aftershocks of the Mw 7.6 Bhuj Earthquake of Bhuj Earthquake of January 26, 2001. Bulletin of the Seismological Society of America, 94, 818-827. http://dx.doi.org/10.1785/0120030176
- 20. Hanks, T.C. and Kanamori, H. (1979) A Moment-Magnitude Scale. Journal of Geophysical Research, 84, 2348-2350. http://dx.doi.org/10.1029/JB084iB05p02348
- 21. Ben-Menahem, A., Smith, S.W. and Teng, T.L. (1965) A Procedure for Source Studies from Spectrums of Long Period Seismic Body Waves. Bulletin of the Seismological Society of America, 55, 203-235.
- 22. Keilis-Borok, V.I. (1959) An Estimation of the Displacement in an Earthquake Source and of Source Dimensions. Annali di Geofisica, 12, 205-214.
- 23. Richter, C.F. (1958) Elementary Seismology. W.H. Freeman, San Francisco, 768.
- 24. Archileta, R.J., Cranswick, E., Muellar, C. and Spudich, P. (1982) Source Parameters of the 1980 Mammoth Lakes, California, Earthquake Sequence. Journal of Geophysical Research, 87, 4595-4607.
http://dx.doi.org/10.1029/JB087iB06p04595 - 25. Hanks, T.C., Hileman, J.A. and Thatcher, W. (1975) Seismic Moment of Larger Earthquakes of the Southern California Region. Geological Society of America Bulletin, 86, 1131-1139.
2.0.CO;2>http://dx.doi.org/10.1130/0016-7606(1975)86<1131:SMOTLE>2.0.CO;2 - 26. Izutani, Y. (2005) Radiated Seismic Energy from the Mid Niigata, Japan, Earthquake of October 23, 2004 and Its Aftershocks. Geophysical Research Letters, 32, Article ID: L21313.
http://dx.doi.org/10.1029/2005GL024116 - 27. Mayeda, K.M., Yoo, S., Walter, W.R., G?k, R.M. and Malagnini, L. (2012) Improved High Frequency Discrimination: A New Approach to Correct for Regional Source Scaling Variations. 2012 Monitoring Research Review: Ground-Based Nuclear Explosion Monitoring Technologies, 453-458.�
- 28. Kanamori, H. and Rivera, L. (2004) Static and Dynamic Scaling Relations for Earthquake and Their Implications for Rupture Speed and Stress Drop. Bulletin of the Seismological Society of America, 94, 314-319. http://dx.doi.org/10.1785/0120030159
- 29. Walter, W.R., Mayeda, K. and Patton, H. (1995) Phase and Spectral Ratio Discrimination between NTS Earthquakes and Explosions, Part I: Empirical Observations. Bulletin of the Seismological Society of America, 85, 1050-1067.
- 30. Abe, K. (1975) Determination of Static and Dynamic Fault Parameters of the Saitama Earthquake of July, 1968. Tectonophysics, 27, 223-238. http://dx.doi.org/10.1016/0040-1951(75)90018-9
- 31. Abercrombie, R. (1995) Earthquake Source Scaling Relationships from ?1 to 5 ML Using Seismograms Recorded at 2.5-km Depth. Journal of Geophysical Research, 100, 15-24.
http://dx.doi.org/10.1029/95JB02397 - 32. Boatwright, J. and Choy, G.L. (1986) Teleseismic Estimates of the Energy Radiated by Shallow Earthquakes. Journal of Geophysical Research, 91, 2095-2112.
http://dx.doi.org/10.1029/JB091iB02p02095 - 33. Choy, G.L. and Botwright, J.L. (2012) Radiated Seismic Energy and Energy Magnitude. In: Bormann, P., Ed., New Manual of Seismological Observatory Practice (NMSOP-2), IASPEI, GFZ German Research Centre for Geosciences, Potsdam, 1-9.
- 34. Gutenberg, B. and Richter, C.F. (1956) Earthquake Magnitude, Intensity, Energy and Acceleration. Bulletin of the Seismological Society of America, 46, 105-145.
- 35. Choy, G.L. and Boatwright, J.L. (1995) Global Patterns of Radiated Seismic Energy and Apparent Stress. Journal of Geophysical Research, 100, 18205-18228. http://dx.doi.org/10.1029/95JB01969
- 36. Ide, S., Beroza, G., Prejean, S. and Ellsworth, W. (2003) Apparent Break in Earthquake Scaling Due to Path and Site Effects in Deep Borehole Recordings. Journal of Geophysical Research, 108, 2271. http://dx.doi.org/10.1029/2001jb001617
- 37. Allmann, B.P. and Shearer, P.M. (2009) Global Variations of Stress Drop for Moderate to Large Earthquakes. Journal of Geophysical Research, 114, Article ID: B01310.
- 38. Prieto, G.A., Thomson, D., Vernon, F., Shearer, P. and Parker, R. (2007) Confidence Intervals for Earthquake Source Parameters. Geophysical Journal International, 168, 1227-1234.
http://dx.doi.org/10.1111/j.1365-246X.2006.03257.x - 39. Sonley, E. and Abercrombie, R.E. (2006) Effects of Methods of Attenuation Correction on Source Parameter Determination. In: Abercrombie, R., Ed., Earthquakes: Radiated Seismic Energy and the Physics of Faulting, AGU, Washington DC, 91-97. http://dx.doi.org/10.1029/170GM11
- 40. Mandal, P., Rastogi, B.K., Satyanarayan, H.V.S. and Kousalya, M. (2004) Results from Local Earthquake Velocity Tomography: Implications toward the Source Process Involved in Generating the 2001 Bhuj Earthquake in the Lower Cruts Beneath Kachchh (India). Bulletin of the Seismological Society of America, 94, 633-649. http://dx.doi.org/10.1785/0120030056
- 41. Rice, J.R. (1990) Fault Stress States, Pore Pressure Distributions and the Weakness of the San Andreas Fault (Abstract). Eos, Transactions American Geophysical Union, 71, 1652.
NOTES
*Corresponding author.













