International Journal of Geosciences
Vol.05 No.13(2014), Article ID:52330,12 pages
10.4236/ijg.2014.513128
Assessment of the Relationships among Catchments’ Morphometric Parameters and Hydrologic Indices
Sotirios Karalis, Efthimios Karymbalis, Kanella Valkanou, Christos Chalkias, Petros Katsafados, Kleomenis Kalogeropoulos, Vasileios Batzakis, Antonios Bofilios
Department of Geography, Harokopio University of Athens, Athens, Greece
Email: skaralis@teiath.gr, karymbalis@hua.gr, kvalkanou@hua.gr, xalkias@hua.gr, pkatsaf@hua.gr, kalogeropoulos@hua.gr, mpatzakis@gmail.com, bofiliosa@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 October 2014; revised 2 November 2014; accepted 25 November 2014
ABSTRACT
In Greece the hydrological analysis of ephemeral streams has been especially difficult due to the lack of precipitation and discharge gauges. This study focuses on the investigation of possible relationship between morphometric characteristics of small to medium drainage basins and hydrological indices in order to discover morphometric parameters “predictors” of flash flood potential of ungauged catchments. Twenty-two morphometric parameters of twenty-seven drainage basins (ranging in area between 3.6 km2 and 330.5 km2) located in the northern part of the Peloponnese in southern Greece were calculated utilizing GIS software ArcGIS10. Hydrological modeling was performed using a simplified Matlab implementation of TOPMODEL, a conceptual model based on the principle of variable contributing area to runoff production through saturated overland flow, and LISEM, a physically based hydrologic and soil erosion model. Rainfall-runoff simulations were performed for an extreme precipitation event. The simulations outcomes, which include the peak discharge, time to peak and the percentage runoff, were correlated with the morphometric parameters of the catchments. Results were not consistent between the two models, probably due to their different structure, with the LISEM results being closer to what is anticipated. The results demonstrate that area, length of the basin, perimeter and compactness factor appear better correlated with the peak discharge (Qpeak) of the catchment. The same parameters as well as Melton’s number correlate with percentage runoff (C), while “celerity” of the flood wave (length of the basin/time to peak) is better correlated with relief, indicating that as the relief becomes greater, the response of the basin becomes fastest.
Keywords:
Geomorphometry, Hydrologic Modeling, TOPMODEL, LISEM, Greece

1. Introduction
In Greece a lot of drainage basins are relatively small with steep slopes, configured by torrents with braided main channel morphology. These systems for most of the year are usually dry or of low discharge but become particularly active during extreme flash flood events of low frequency but high magnitude. Such exceptionally high runoff may be a source of significant damage and serious loss to human infrastructures. Despite the importance of these floods, the hydrological analysis of ephemeral streams has been especially difficult due to the lack of precipitation and discharge gauges [1] . Therefore any analysis of flood balances of isolated events contributes to a better understanding of the processes involved in the genesis of extreme runoff.
Generally the floods in the Mediterranean area are linked to climatologic events, but there are some factors which can intensify the flood phenomenon. Among them, the geomorphological characteristics of the drainage network, the morphology of the catchment and human interventions are the most important. On a qualitative basis, it is well known that hydrologic processes are influenced by the organization of the drainage networks as well as by the geomorphometric properties of the catchments [2] - [4] . Many previous studies deal with the investigation of the relations between drainage basin parameters and hydrologic indices [2] [5] and have tried to establish the link between the hydrological response of a catchment and descriptors of its physical attributes [4] [6] - [8] .
Fluvial forms are the result of a long process of drainage basin evolution under the action of water and thus interrelationships should exist between morphometric parameters and discharge. The determination of these interrelationships is very useful in making regional generalizations and forecasts, as well as in deriving hydrological data for rivers especially if no direct measurements are available [9] . Additionally there are relations between drainage basin morphometric parameters and flood potential which are significant for flood forecasting in ungauged basins. Some correlation based approaches attempt to quantify the relations among drainage basin parameters and hydrologic indices [10] . However, a general quantification of these effects is still a research task.
The aim of this study is to investigate―through hydrological modeling―the role of the geomorphometric characteristics of the drainage basins, expressed through quantitative morphometric parameters, in the generation of extreme surface runoff. Among the principal objectives of this paper is to discover the potential existence of “predictor” parameters of the flooding potential of small to medium size catchments. For this purpose twenty- two morphometric variables describing twenty-seven drainage basins are examined and their relationships with hydrologic indices, derived from the hydrologic models TOPMODEL and LISEM, are investigated.
2. Study Area
This study focuses on twenty-seven drainage basins, ranging in area between 3.6 km2 and 330.5 km2, located in northern Peloponnese in southern Greece (Figure 1). The main channels of the drainage networks follow a SSE- NNW flow direction and discharge into the Gulf of Corinth.
The Corinth rift is considered to be the most active neotectonic feature within the Eastern Mediterranean [11] [12] . Active faulting on the southern side of the Gulf has resulted in more than 950 m of Pleistocene uplift of the mountains in the south, where the investigated catchments are located. The area of the southern part of the basins consists of geological formations of Mesozoic age (mainly limestones, but also cherts and flysch layers which belong to the geotectonic zones of Olonos-Pindos and Gavrovo-Tripolis, respectively). The northern part of the catchments is dominated by Late Pliocene fluvial and lacustrine sands, silts and conglomerates, passing upwards to Quaternary marls and Gilbert-fan delta conglomerates [13] .
The climate of the north Peloponnese is coastal Mediterranean (Köppen: Csb) with mean annual temperature 14.5˚C, mean temperature of the coldest month 10.6˚C and mean temperature of the warmest month 26.4˚C. Rainfall exhibits a strong gradient in the west-east direction ranging from more than 1500 mm of rain over the mountains of central Peloponnese to less than 450 mm in the east [14] .
Some of the streams have perennial flow but many are torrents with only ephemeral flow. Parts of the catchments, especially along the lower reaches of some of these streams, have often suffered extensive flooding during extreme rainfall events. The most severe floods happened on January 11th and 12th 1997 and caused loss of life for six people and extensive damage of houses especially in the city of Corinth, at the lower reaches of Xerias river [4] . The drainage basins, with the exception of Vouraikos River catchment, are not monitored. Hence there are no available measurements of precipitation and water discharge for the flash food events that have affected the catchments.
Figure 1. Location of drainage basins in the study area.
3. Methodology
3.1. Geomorphometric Analysis
Quantitative geomorphic methods can provide means of measuring size and form properties of drainage networks and basins. In this study the geomorphometric analysis of the investigated catchments was carried out with GIS software ArcGIS10.
The twenty-two morphometric parameters used in this study are shown in Table 1. They were calculated through the 25 m × 25 m resolution DEM. According to [15] there are two general classes of calculated parameters that can be correlated to hydrologic data 1) linear scale measurements as the area of the basin, the perimeter of the basin, the maximum elevation of the basin, the elevation at the outlet, the total length of channels within the basin, the total length of 20 m contour lines within the basin, the slope of the basin, the drainage density, the basin’s relief, the mean elevation of the watershed, the elevation of the centroid, the length of the longest flow path in the basin and the slope of the longest flow path and 2) dimensionless numbers as the Melton’s ruggedness number, the basin’s circularity, the elongation ratio, the relief ratio, the index of ruggedness based on relief and other relief ratios.
3.2. Hydrologic Modeling
Hydrologic modeling was conducted using two rainfall-runoff models: TOPMODEL and LISEM.
TOPMODEL is an example of a conceptual approach. The version that is used in this study is a simplified MATLAB implementation of TOPMODEL [26] .
TOPMODEL is based on the idea that topography exerts a dominant control on flow routing through upland catchments [27] . For TOPMODEL stream-flow is the sum of subsurface flow and of overland flow from saturated contributing areas:
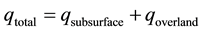
The important characteristics of a hillslope that influence the likelihood of areas of saturation developing are the upslope “contributing area” and the slope of the block. The effect of topography is quantitatively captured by the Topographic Index (TI), defined as:
Table 1. Morphometric parameters of drainage basins calculated for this study. A short description of the parameters as well as their symbols and formulas are also given. (e is the equidistant of contour lines −20 m).

where
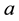 is the upslope contributing area per unit contour length
is the upslope contributing area per unit contour length
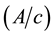 and
and
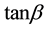 is the local slope.
is the local slope.
The most significant parameters of TOPMODEL are m [L] and T [L2T−1], and they are both physical soil parameters (for a discussion of the parameters, see [28] ). The selection of
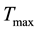 and
and
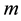 values was based on visual inspection and comparison of the observed and simulated hydrographs at the hydrological station of Zachlorou in the gauged basin of Vouraikos River (Figure 2), located in the western part of the study area (Figure 1). The values of the main parameters
values was based on visual inspection and comparison of the observed and simulated hydrographs at the hydrological station of Zachlorou in the gauged basin of Vouraikos River (Figure 2), located in the western part of the study area (Figure 1). The values of the main parameters
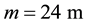 and
and
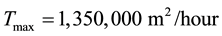 were derived from this calibration, and used throughout the 29 simulations.
were derived from this calibration, and used throughout the 29 simulations.
Since many of the catchments were large and rather elongated, we included a routing module in the model. This routing module accounted for simple translation of the hydrograph.
LISEM, after Limburg Soil Erosion Model [29] [30] is a physically-based hydrologic and soil erosion model operating at the catchment scale. The model has been designed to simulate runoff and erosion as a consequence
Figure 2. The observed and simulated hydrographs of a rainfall event at the hydrological station of Zachlorou in Vouraikos River basin. The comparison of these hydrographs led to the selection of the values of m and Tmax.
of single rainstorms in agricultural catchments of a size ranging from 1 ha up to approximately 100 km2, but it has been also used in larger basins.
The model is one of the first examples of a physically based model that is completely integrated in a raster Geographical Information System, PCRaster [31] . LISEM needs a minimum of 24 raster maps depending on the input options selected in the interface.
A raster grid-cell can have more than one type of surface. The infiltration characteristics vary according to the surface and the infiltration is calculated for each type. An average water height is then calculated for each grid- cell, resulting in an average hydraulic radius with which the velocity is calculated. The velocity
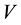 (m/s) is calculated with Manning’s formula:
(m/s) is calculated with Manning’s formula:
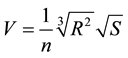
in which: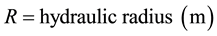 , calculated with the flow width and average water height;
, calculated with the flow width and average water height;
 sine of the slope (fraction);
sine of the slope (fraction);


The discharge

in which
and


For the distributed overland and channel flow routing, a four-point finite-difference solution the kinematic wave is used together with Manning’s equation. The kinematic wave is done over the Local Drain Directions map that forms a network which connects cells in 8 directions.
In our application LISEM was used as a rainfall-runoff model, assuming no infiltration or canopy retention since we were interested in the effects of landscape topography alone (after all, this is what the morphometric parameters describe). No explicit parameters were thus needed in the model, except from values of Manning’s n. The time step of the LISEM model runs was one minute.
In this study, three hydrological indices were considered, namely Qpeak (peak discharge), which was the largest value of the discharge in the simulated hydrograph (in mm), the percentage runoff (C = discharge/rainfall) and the time to peak (number of hours that the peak discharge lagged after the rainfall peak). In order to scale time to peak to the dimensions of the basins, one more index, the “celerity” of the flood wave (length of the longest flow path/time to peak) was also calculated. This was only possible for LISEM results due to fine detail of the time to peak that was given in minutes.
4. Results and Discussion
The values of the morphometric variables of the catchments are presented in Table 2. The same table includes the hydrologic indices derived from the simulated flood hydrographs of the extreme rainfall event (80 mm in 3 hours) derived from the application of TOPMODEL and LISEM.
The identification of all the possible paired relationships between the morphometric characteristics of the catchments and the hydrologic parameters for the drainage basins of the study area was attempted with the calculation of the values of the correlation coefficients (Table 3(a) for TOPMODEL and Table 3(b) for LISEM).
With respect to the significance of geomorphometric properties in hydrology and flood processes, scaling effects have to be considered. Spatial thresholds affecting changes in runoff-morphometry relations have to be determined. For this, the drainage basins of the study area were grouped into three groups: small catchments with an area lower than 10 km2, medium-sized catchments having an area between 10 and 100 km2 and large basins with an area larger than 100 km2.
The two models produced qualitative different correlations among catchment morphometric parameters and hydrologic indices. In particular, due to its internal structure (the calculation of the TI), TOPMODEL predicts a strong negative correlation between the slope of the basin (Sl) and the peak discharge










LISEM runs give a different, more “intuitive” view. In these results, peak discharge
















LISEM results better fit to our understanding of an extreme flood event in a dry or semidry environment, dominated by a large proportion of overland, infiltration excess (Hortonian) type of flow.
It is interesting at this point to examine some of the LISEM hydrographs in order to gain an insight into the outcomes of the simulations. We will consider three examples, one for small size basins, one for medium size basins and one for large basins (location of basins in Figure 3).
In Figure 4(a) we see the hydrographs for two small catchments that have nearly the same area, but behave very differently. Anonymous 5 has a much larger flood response and also a greater time lag. This can be “predicted” by the differing morphometry of the two catchments.
Table 2.Values of selected morphometric parameters for the investigated drainage basins.Hydrologic indices derived from the simulated flood hydrographs of the extreme rainfall event are also included for TOPMODEL and LISEM.
Table 3. Correlation matrix of morphometric catchment parameters and hydrological parameters derived from simulated hydrographs after the application of TOPMODEL (a) and LISEM (b); for all twenty-seven basins as well as for each one of the three drainage basins’ groups: small catchments (<10 km2), medium catchments (10 - 100 km2) and large catchments (>100 km2). The best correlation results of the analysis (with correlation coefficient > 0.7) are marked with red while moderate correlations (0.5 < correlation coefficient < 0.7) are marked in yellow color.
Figure 3. Location of basins selected for (LISEM) hydrograph analysis.
Even though no significant correlations between geomorphometric parameters and peak discharge




In Figure 4(b) the hydrographs of two medium size catchments are shown that are very close with regards to their morphometric characteristics. In such cases we could look for morphometric characteristics that differ greatly, like for instance, in this case, relief





In Figure 5 we see the original hydrographs on the left (discharge in m3/s), while on the right we have normalized them for their respective area (discharge in mm/hr). The normalized hydrographs reveal that the lowest runoff producing basin is Vouraikos which is consistent with the strong negative correlation of peak discharge


When studying the LISEM correlation matrix, we note that correlations of peak discharge








Time to peak correlates well with perimeter, and the flood wave “celerity” (length of the longest flow path/

Figure 4. Comparison of hydrographs: (a) for two small size basins; (b) for two medium size basins.

Figure 5. Comparison of three large basins’ hydrographs (original and normalized values).
Figure 6. Compactness factor?Peak discharge scatter plot for medium and large basins.
time to peak) correlates well with relief (Figure 7(a)). This is somehow expected, since a larger elevation difference will force the flood quickly towards the outlet.
Percentage runoff correlates well with relief ratios (relief divided by the length of the longest flow path-di- mensionless) and Melton’s number (Figure 7(b)), also dimensionless.
5. Conclusions
The main research idea was to identify geomorphometric parameters on the catchment scale termed “representative geomorphometric parameters” that have hydrologic relevance (“effective parameters”). Two rainfall-runoff models (TOPMODEL and LISEM) were employed to run simulations for a set of 27 ungauged torrential catchments in North Peloponnese. These models are highly dependent on topography, either implicitly (TOPMODEL through the definition of TIs) or explicitly (LISEM through the kinematic wave solution of overland flow), but

Figure 7. (a) Relief - celerity plot for all basins; (b) Melton’s ruggedness number - percentage runoff scatter plot for all basins.
differ both in temporal detail and also in the consideration of the runoff mechanisms. The comparison of the correlation coefficients between the catchments’ geomorphometric parameters and the hydrologic indices revealed that among the two models, LISEM is more suitable for the simulation of extreme flood events in mountainous torrential steams of a semi-arid environment (like the study area in North Peloponnese) dominated by a large proportion of overland, Hortonian type of flow.
The strong correlation coefficients among some of the morphometric parameters and the hydrologic indices derived from the LISEM runs showed that morphometric analysis is crucial in any hydrological investigation and that there are relationships between some geomorphometric parameters and flash flood response as well as flood potential of torrential drainage basins. Hence the estimation of some basin parameters (compactness factor, relief, relief ratio and Melton’s number) can lead to effective prediction of some hydrologic indices regarding flooding. More specifically compactness factor is a good predictor for flash-flood peak discharge


Some issues, unaddressed in this study (most importantly, the effect of the boundary conditions?parameters and rainfall event?, the sensitivity of the model results, the effect of raster size in the calculation of the morphometric parameters and the size of the sample) can be explored in further studies, as far as this report is considered as a first step in an ongoing research.
Acknowledgements
The authors are grateful to the Research Committee of the Harokopio University of Athens, Greece, for funding the project that is described in this paper. The authors would also like to thank the reviewers for their constructive comments and the Editor of the journal.
References
- Karymbalis, E., Chalkias, C., Ferentinou, M. and Maistrali, A. (2011) Flood Hazard Evaluation in Small Catchments Based on Quantitative Geomorphology and GIS Modeling: The Case of Diakoniaris Torrent (W. Peloponnese, Greece). In: Lambrakis, N., Stournaras, G. and Katsanou, K., Ed., Advances in the Research of Aquatic Environment, Environmental Earth Sciences, Springer-Verlag, Berlin Heidelberg, 137-145. http://dx.doi.org/10.1007/978-3-642-19902-8_15
- Gregory, K.J. and Walling, D.E. (1973) Drainage Basin. Form and Process: A Geomorphological Approach. Edward Arnold, London.
- Howard, A.D. (1990) Role of Hypsometry and Planform in Basin Hydrologic Response. Hydrological Processes, 4, 373-385. http://dx.doi.org/10.1002/hyp.3360040407
- Karymbalis, E., Katsafados, P., Chalkias, C. and Gaki-Papanastassiou, K. (2012) An Integrated Study for the Evaluation of Natural and Anthropogenic Causes of Flooding in Small Catchments Based on Geomorphological and Meteorological Data and Modeling Techniques: The Case of the Xerias Torrent (Corinth, Greece). Zeitschrift für Geomorphologie, 56, 045-067. http://dx.doi.org/10.1127/0372-8854/2012/S-00072
- Cooke, R.U. and Doornkamp, J.C. (1990) Geomorphology in Environmental Management. 2nd Edition, Oxford University Press, Oxford.
- Post, D.A. and Jakeman, A.J. (1996) Relationships between Catchment Attributes and Hydrological Response Characteristics in Small Australian Mountain Ash Catchments. Hydrological Processes, 10, 877-892.
- Post, D.A. and Jakeman, A.J. (1999) Predicting the Daily Streamflow of Ungauged Catchments in SE Australia By Regionalizing the Parameters of a Mumped Conceptual Rainfall-Runoff Model. Ecological Modelling, 123, 91-104. http://dx.doi.org/10.1016/S0304-3800(99)00125-8
- Runge, J. and Nguimalet, C.R. (2005) Physiogeographic Features of the Oubangui Catchment and Environmental Trends Reflected in Discharge and Floods at Bangui 1911-1999, Central African Republic. Geomorphology, 70, 311- 324. http://dx.doi.org/10.1016/j.geomorph.2005.02.010
- Zăvoianu, I. (1985) Morphometry of Drainage Basis, Developments in Water Science, 20. Elsevier Publications, Amsterdam, 4-5.
- Moore, I.D., Grayson, R.B. and. Ladson, A.R. (1991) Digital Terrain Modelling: A Review of Hydrological, Geomorphological and Biological Applications. Hydrological Processes, 5, 3-30. http://dx.doi.org/10.1002/hyp.3360050103
- Armijo, R., Meyer, B., King, G., Rigo, A. and Papanastassiou, D. (1996) Quaternary Evolution of the Corinth Rift and Its Implications for the Late Cenozoic Evolution of the Aegean. Geophysical Journal International, 126, 11-53. http://dx.doi.org/10.1111/j.1365-246X.1996.tb05264.x
- McNeil, L. and Collier, R. (2004) Uplift and Slip Rates of the Eastern Eliki Fault Segment, Gulf of Corinth, Greece, Inferred from Holocene and Pleistocene Terraces. Journal of the Geological Society, 161, 81-92. http://dx.doi.org/10.1144/0016-764903-029
- Bornovas, I. and Rondoyanni, Th. (1983) Geological Map of Greece, Scale 1:500,000. Institute of Geology and Mineral Exploration, Athens.
- Katsafados, P., Kalogirou, S., Papadopoulos, A. and Korres, G. (2012) Mapping Long-Term Atmospheric Variables over Greece. Journal of Maps, 8, 181-184. http://dx.doi.org/10.1080/17445647.2012.694273
- Strahler, A.N. (1957) Quantitative Analysis of Watershed Geomorphology. Transactions, American Geophysical Union, 38, 913-920. http://dx.doi.org/10.1029/TR038i006p00913
- Horton, R.E. (1945) Erosional Development of Streams and Their Drainage Basins: Hydrophysical Approach to Quantitative Morphology. Geological Society of America Bulletin, 56, 275-370. http://dx.doi.org/10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2
- Roche, M. (1963) Hydrology de Surface. Gauthier-Villars, Paris.
- Strahler, A.N. (1952) Dynamic Basis of Geomorphology. Geological Society of America Bulletin, 63, 923-938. http://dx.doi.org/10.1130/0016-7606(1952)63[923:DBOG]2.0.CO;2
- Black, P.E. (1996) Watershed Hydrology. 2nd Edition, Ann Arbor Press, Chelsea.
- Schumm, S.A. (1956) Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geological Society of America Bulletin, 67, 597-646.
- Melton, M.A. (1965) The Geomorphic and Palaeoclimatic Significance of Alluvial Deposits in Southern Arizona. Journal of Geology, 73, 1-38. http://dx.doi.org/10.1086/627044
- Church, M. and Mark, D.M. (1980) On Size and Scale in Geomorphology. Progress in Physical Geography, 4, 342- 390. http://dx.doi.org/10.1177/030913338000400302
- Miller, V.C. (1953) A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee. Department of Geology Columbia University, New York, 389-402.
- Gravelius, H. (1914) Grundrifi der gesamten Gewcisserkunde. Band I: Flufikunde (Compendium of Hydrology, Vol. I. Rivers, in German). Goschen, Berlin.
- Strahler, A.N. (1968) Quantitative Geomorphology. In: Fairbridge, R.W., Ed., The Encyclopedia of Geomorphology, Reinhold Book Crop., New York.
- Hornberger, G.M., Raffensperger, J.P., Wiberg, P.L. and Eshleman, K.N. (1998) Elements of Physical Hydrology. The Johns Hopkins University Press, Baltimore and London.
- Beven, K.J. and Kirkby, M.J. (1979) A Physically Based Variable Contributing Area Model of Basin Hydrology. Hydrological Sciences Bulletin, 24, 43-69. http://dx.doi.org/10.1080/02626667909491834
- Beven, K. (1997) TOPMODEL: A Critique. Hydrological Processes, 11, 1069-1085. http://dx.doi.org/10.1002/(SICI)1099-1085(199707)11:9<1069::AID-HYP545>3.0.CO;2-O
- De Roo, A.P.J., Wesseling, C.G. and Ritsema, C.J. (1996) LISEM: A Single Event Physically-Based Hydrologic and Soil Erosion Model for Drainage Basins: I. Theory, Input and Output. Hydrological Processes, 10, 1107-1117. http://dx.doi.org/10.1002/(SICI)1099-1085(199608)10:8<1107::AID-HYP415>3.0.CO;2-4
- De Roo, A.P.J., Offermans, R.J.E. and Cremers, N.H.D.T. (1996) LISEM: A Single Event Physically-Based Hydrologic and Soil Erosion Model for Drainage Basins: II. Sensitivity Analysis, Validation and Application. Hydrological Processes, 10, 1119-1126. http://dx.doi.org/10.1002/(SICI)1099-1085(199608)10:8<1119::AID-HYP416>3.0.CO;2-V
- Van Deursen, W.P.A. and Wesseling, C.G. (1992) The PC-Raster Package. Department of Physical Geography, Utrecht University. http://www.pcraster.nl
- Chow, V.T., Maidment, D. and Mays, L. (1988) Applied Hydrology. McGraw Hill International Editions, New York.












