International Journal of Geosciences
Vol.05 No.11(2014), Article ID:50422,8 pages
10.4236/ijg.2014.511104
A Micro Study to Determine Porosity, Hydraulic Conductivity, Permeability and the Discharge Rate of Groundwater in Ondo State Riverbeds, Southwestern Nigeria
Akintayo D. Omojola, Sunday J. Akinpelu, Abisola M. Adesegun, Olukayode D. Akinyemi
Department of Physics, College of Natural Sciences, Federal University of Agriculture, Abeokuta, Nigeria
Email: akintayoomojola@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2014; revised 11 September 2014; accepted 5 October 2014
ABSTRACT
Laboratory study of three riverbed soil samples denoted as A, B and C have been carried out by determining the soils Porosity, Hydraulic conductivity, Permeability and also investigating if there are points of convergence between the discharge rate and angle of tilt for the above mentioned samples. The experimental results for Porosity were approximately within 34% - 37%, Hydraulic conductivity was within 3.02 × 10−5 - 9.70 × 10−5 (m/s) and Permeability was within 2.74 × 10−12 - 8.80 × 10−12 (m2). Pressure generally increases as distance of flow increases for θ = 5˚ - 25˚ but there was decrease in pressure as distance of flow increases for all three samples when θ = 0˚. The points of convergence for the discharge rate ranged from 0.001 × 10−10 - 4.54 × 10−10 (m3/s), while the angle of tilt convergence points ranged from 0.1˚ to 3.6˚. There was increase in discharge rate as angle of tilt increases for all three samples.
Keywords:
Pressure Digital Manometer, Pressure Gradient, Global Positioning System, Riverbed

1. Introduction
Soil Porosity, Hydraulic conductivity and Permeability play vital roles in determining groundwater movement at any point on the surface of the earth. This in turn determines the discharge rate among other properties. There has been no clear evidence of research work to determine soil properties in Ondo State despite its natural endowments of tree crops, highlands and rocks surrounding the state. This study of flow in porous media helps us to understand and predict the extent of underground water movement based on their properties among other things [1] [2] . Porosity is the fraction of the total soil volume that is taken up by the pore space. Hydraulic conductivity is the rate of flow of water through a cross sectional area under a unit Hydraulic gradient at the prevailing temperature [3] and Permeability is the property or capacity of a porous rock, sediment or soil for transmitting a fluid without impairment of the medium; it is a measure of the relative ease of flow under unequal pressure [3] . Materials that are more solid will reduce the flow rate, while materials that are more porous will increase the flow rate. The rate and direction of groundwater flow at a given location are driven by Hydraulic gradient which in turn is determined by the boundaries of the system and the location and strength of the discharge rate [4] . This work is aimed at determining the Porosity, Hydraulic conductivity, Permeability and also studying the relationship that exists between points of convergences of the discharge rate of groundwater against angle of tilt for three different soil samples from different locations in Ondo State.
Ondo is one of the six states that make up the South West geopolitical zone of Nigeria. It has interstate boundaries with Ekiti and Kogi states to the north, Edo State to the east, Delta State to the southeast, Osun State to the northwest and Ogun State to the southwest. The Gulf of Guinea lies to its south and its capital is Akure. It has a land mass of about 14788.723 square kilometers (Km2) and it geographically lies entirely in the tropical belt. The tropical climate of the state is broadly of two seasons which are the rainy season between April and October and dry season between November and March. A temperature throughout the year ranges between 21˚C to 29˚C and humidity is relatively high. The annual rainfall varies from 2000 mm in the southern areas to 1150 mm in the northern areas. It has vegetation with high forest zone (rain forest) in the south and sub-savannah forest in the northern fringe. Generally, the land rises from the coastal part of Ilaje, Ese-Odo and Okitipupa areas to highlands and inselbergs to the northern parts of the state. Figure 1 shows an aerial view of some parts of Ondo State.
2. Materials and Methods
2.1. Theoretical Background
The governing Darcy’s equation for a flow through a porous material of Permeability [k] can be written as [5] :
 (1)
(1)
This can be expressed as:
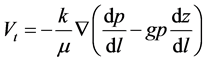 (2)
(2)
where l is the flow directional distance, Vt is the volume flux across a unit area of the porous media in unit time
Figure 1. An aerial view of some part of Ondo State (Courtesy Ondo State ministry of information).
along flow path l, z is a vertical coordinate considered positive downward, P is the liquid density (water) and g is the acceleration due to gravity.  is the pressure gradient along l at the point to which Vt refers, and
is the pressure gradient along l at the point to which Vt refers, and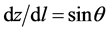 , where θ is the angle between l and the horizontal.
, where θ is the angle between l and the horizontal.
 (3)
(3)
where:
Q = Discharge rate (m3/s);
A = Average cross-sectional area perpendicular to the line of flow (m2).
It follows that:
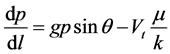 (4)
(4)
For a medium that is completely saturated with an incompressible fluid and is horizontally placed tube, for which 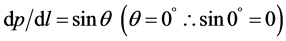 Equations (4) becomes:
Equations (4) becomes:
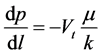 (5)
(5)
2.2. Experimental Methods
Riverbed soil samples were collected from three major areas in Ondo State which is located in the Southwestern part of Nigeria as described in Figure 2. The first sample was collected from Ile-Oluji/Okeigbo, denoted as sample A, the second from Owo denoted as sample B and the third sample from Akoko North-West in Ikare- Akoko denoted as C. These samples were taken undisturbed from the riverbeds by placing a cylindrical metal tin of known weight of length 0.1 m and diameter 4.4 × 10−2 m is opened at both end on the undisturbed fine soil and the metal core were pushed into the soil. The cylindrical tin was removed with the aid of a sharp flat metal material and a thin layer cotton material was used to tie the base of each sample to ensure that the soil sample do not pour out of the cylindrical tin. A global positioning system was used to acquire locations (longitude, latitude and elevation) from which these soils were gotten as described by Table 1. The samples were later taken to the soil department for Hydraulic conductivity and Permeability test, where the constant head method was used. Porosity test was carried out using volumetric approach. A constant height of water of 0.09 was maintained and the discharge rate [Q], drained in the beaker per minute was noted. The Hydraulic conductivity [K] of each sample was then determined since the discharge rate [Q], the length of the sample (height of the soil in the cylindrical tin) [L], cross sectional area of the sample in the cylindrical tin [A], time required for the quantity of water to be discharged [t] and the head constant (height of the water) [h] are known. The Hydraulic conductivity was then calculated using the relation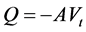 , where V is the flow velocity and using Darcy’s law
, where V is the flow velocity and using Darcy’s law 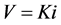 thus by expressing the Hydraulic gradient i as
thus by expressing the Hydraulic gradient i as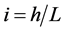 , where h is the head constant and L the flow path length, this gives:
, where h is the head constant and L the flow path length, this gives:
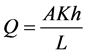 (6)
(6)
Making K subject of the formula gives
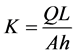 (7)
(7)
Thus Permeability [k] was determined using Hubert King’s relation [6] of the form
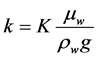 (8)
(8)
where:
μw = Viscosity of water;
ρw = Density of water;
k = Permeability;
K = Hydraulic conductivity;
g = Gravitational constant.
Figure 2. Map of Nigeria showing Ondo State with sample locations.
Table 1. Sample location parameter.
Also the Porosity [f] was determined using volumetric approach. This was done by calculating the soil’s bulk and particle density [7] in which the cylindrical tins with the wet soil were oven dried and weighed. The corresponding weight of the dry soil sample was measured using a sensitive scale weighing balance to get the bulk density and an assumed particle density of 2.65 g/cm3 was used [8] . Equation (9) describes the relation used for calculating the Porosity, which is given as:

A graph of Porosity, Hydraulic conductivity and Permeability was plotted against samples A, B and C as described in Figure 3. Table 2 describes the experimental results for Porosity, Hydraulic conductivity and Permeability.
In another experiment, the materials involved were sample A, B and C, PVC pipes of various lengths and diameters, retort stands, water and a digital pressure manometer. The PVC pipes used for this study were purchase from a local shop with diameters of different range (1.5 × 10−2 m, 2.0 × 10−2 m, 2.7 × 10−2 m, 3.0 × 10−2 m and 3.5 × 10−2 m). Each was cut into five different lengths (L = 0.25 m, 0.5 m, 1.0 m, 2.0 m and 3.0 m), as described in Table 3. The PVC pipes used were as well drilled at intervals [dl] with respect to the various lengths. Length 0.25 m was drilled at an interval of 0.04 m, length 0.5 m at 0.08 m, length 1.0 m at 0.16 m, length 2.0 m at 0.32 m and 3.0 m at 0.48 m. Each sample was loaded into the PVC pipes of various lengths and diameters. An elbow joint was attached to each PVC pipes to make room for an L-shaped structure which store water at constant height of 0.06 m. This height of water was maintained and excess water was drained off through the connected rubber tubing of the digital pressure manometer. The L-shaped PVC pipes were made to stand at angles θ = 0˚,
Table 2. Experimental results for Porosity, Hydraulic conductivity and Permeability.
Figure 3. Flow parameter of the samples.
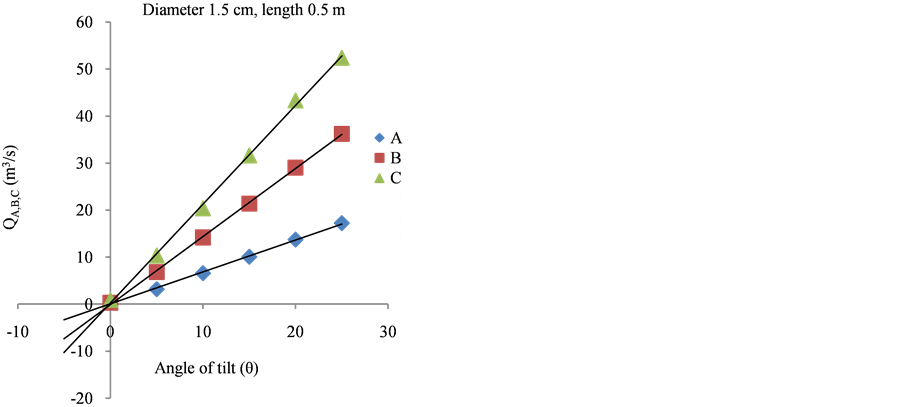
5˚, 10˚, 15˚, 20˚ and 25˚. The digital manometer (with tube diameter of 0.002 m) was connected from the rubber tubing head to the drilled holes on the PVC pipes. Measurements were made at every angle of tilt and the corres- ponding values of the pressures p were determined with respect to the various tube dimensions and the points of intervals. The graphs of dp/dl (N/m3) describe Pressure against distance of flow as illustrated in Figure 4(A), Figure 4(B) and Figures 5(A)-(E). Also, Figures 6(A)-(C) illustrates the graphs of discharge rate against the angles of tilt (θ). Table 4 describes the discharge rates and angles of convergence points for samples A, B & C.
3. Results and Discussion
Table 2 describes the experimental result for Porosity, Hydraulic conductivity and Permeability. The experimental results for the Porosity for sample A, B and C were within approximately 34% - 37%. These values were consistent [9] -[13] . The experimental results for the Hydraulic conductivity were within 3.02 × 10−5 - 9.70 × 10−5 (m/s); these values were within range [8] [14] . Also, the values for Permeability were also within 2.74 × 10−12 - 8.80 × 10−12 (m2) which was within range [15] . It was observed that Porosity increases gradually from sample A-C as seen in Table 2 and Figure 3 respectively. This point to the fact that there exist similar soil characteristic types between all three samples. The Porosity percentage difference between sample A and B was 1.5%, that of sample A and C was 1.6% and that of B and C was 3.1%. Table 2 and Figure 3 also reveal that there was an increase in Hydraulic conductivity and Permeability respectively. This generally implies that as Porosity increases, Hydraulic conductivity and Permeability will as well increase.
At θ = 0˚, there was generally slight decrease in pressure as distance of flow increases for all three samples A, B and C in Figure 4(A), Figure 4(B) and Figures 5(A)-(E). Sample C of diameter 1.5 cm and length 0.25 m in Figure 4(A) when θ = 0˚ had the highest fall in pressure gradient in which dp/dl = −3.15 and the least fall in pressure gradient was recorded in sample A of diameter 3.5 cm and length 0.25 m in Figure 4(B), whose pressure gradient was dp/dl = −0.35. Also in Figure 5(A), for θ = 0˚, sample A of diameter 1.5 cm and length 0.5 m
Table 3. Length parameter in meters (m) for the PVC pipes.

Figure 4. (A) Pressure gradient with the highest fall at 0˚; (B) Pressure gradient with the least fall at 0˚.



Figure 5. (A) Pressure gradient with the highest fall at 0˚; (B) Pressure gradient with the least fall at 0˚; (C) Pressure gradient with the least fall at 0˚; (D) Pressure gradient with the least fall at 0˚; (E) Pressure gradient with the least fall at 0˚.
Table 4. Discharge rates and angles of convergence for sample A, B and C.
D = Diameter of PVC pipe; L = Length of PVC pip; Q = Discharge rate (m3/s); θ = Angle of convergence in degree.


Figure 6. (A) Least discharge rate at [QAB] and one of the least angles of tilt at [θAB]; (B) Highest discharge rate at [QBC]; (C) Highest angle of tilt at [θAB].
had the highest fall in pressure gradient where dp/dl = −0.65 while the least fall in pressure gradient was the same in Figures 5(B)-(E) respectively with dp/dl = −0.125. It was observed that pressure increases with increase in distance of flow for θ = 0˚ – 25˚ for samples A, B and C for both length and diameter [16] .
Convergence points of discharge rate against angle of tilt were observed between samples QAB, QAC, QBC, and QAB, QAC, QBC as illustrated in Table 4. A point was observed where QAB = QAC = QBC = 0.6˚ which was independent of discharge rate. The convergence point for the discharge rate ranged from 0.001 × 10−10 (m3/s) to 4.45 × 10−10 (m3/s) while the angle of tilt convergence point ranged from 0.1˚ to 3.6˚. Figure 6(A) showed the least discharge rate and one of the least angles of tilt, Figure 6(B) showed the highest discharge rate and Figure 6(C) showed the highest angle of tilt.
4. Conclusion
The study of these riverbed sediments in Ondo State which is located in the Southwestern region of Nigeria reveals that there exist close soil types going by the values obtained for Porosity. This might be attributed to common sources of flow and other factors. It was also noticed that as Porosity increases, Hydraulic conductivity and Permeability increases. The Porosity of sample A, B and C soil types fell within silt [11] -[13] . Hydraulic conductivity and Permeability fell within silty sand and fine∕clean sand as described by [15] . This study showed that the discharge rates for the three soil samples were low, meaning that more water was absorbed. This explains the reason why this region is categorized as high forest zone and the growing of tree crops. There is a need for more research work to be done in this region since their main stay is agriculture; this will help predict groundwater movement and how to harness its use.
References
- Mirus, B.B., Perkins, K.S., Nimmo, J.R. and Singha, K. (2009) Hydrologic Characterization of Desert Soils with Varying Degrees of Pedogenesis 2, Inverse Modeling for Effective Properties. Vadose Zone Journal, 8, 496-509. http://dx.doi.org/10.2136/vzj2008.0051
- Zhu, J. and Sun, D. (2009) Effective Soil Hydraulic Parameters for Transient Flows in Heterogeneous Soils. Vadose Zone Journal, 8, 301-309. http://dx.doi.org/10.2136/vzj2008.0004
- American Geological Institute (1972) Glossary of Geology.
- Morin, R.H. (2006) Negative Correlation between Porosity and Hydraulic Conductivity Insand-and-Aquifers at Cape Cod, Massachusetts, USA. Journal of Hydrology, 136, 52.
- Frick, T.C. and Taylor, R.W. (1978) Petroleum Production Handbook. McGraw-Hill Book Co, Boston, 23.
- Ghildyal, B.P. and Tripathi, R.P. (1987) Soil Physics. Wiley Eastern, New Delhi, 286.
- Blake, G.R. and Hartge, K.H. (1986) Methods of Soil Analysis. Part 1. Physical and Mineralogical Methods. In: Klute, A., Ed., Soil Science Society of America, 2nd Edition, Madison, 363-375.
- Stephens, D.B., Hsu, K.C., Prieksat, M.A., Ankeny, M.D., Blandford, M., Roth, T.L., Kelsey, J.A. and Whitworth, J.R. (1998) A Comparison of Estimated and Calculated Effective Porosity. Journal of Hydrology, 6, 156-165.
- Fetter, C.W. (1993) Contaminant Hydrogeology. Macmillan Publishing Company, New York.
- Domenico, P.A. and Schwartz, F.W. (1990) Physical and Chemical Hydrogeology. John Wiley and Sons, New York, 824.
- Freeze, R.A. and Cherry, J.A. (1979) Groundwater. Prentice-Hall, Englewood Cliffs, 604.
- Todd, D.K. (1980) Groundwater Hydrology. 2nd Edition, John Wiley, New York, 535.
- Driscoll, F.G. (1986) Groundwater and Wells. 2nd Edition, Johnson Division, St Paul, 1089.
- Gupta, S., Mohanty, B.P. and Köhne, J.M. (2006) Soil Hydraulic Conductivities and Their Spatial and Temporal Variations in a Vertisol. Soil Science Society of America Journal, 70, 1872-1881.
- West, T.R. (1995) Geology Applied to Engineering. 1st Edition, Prentice-Hall, Upper Saddle River, 560.
- Akinyemi, O.D., Akinpelu, S.J. and Adesegun, A.M. (2012) Permeability of Abeokuta Riverbed Sediments. Special Topics. Reviews in Porous Media: An International Journal, 3, 289-296.