International Journal of Geosciences
Vol.5 No.7(2014), Article
ID:46971,10
pages
DOI:10.4236/ijg.2014.57062
Variability of Sand Mobility Surrounding Cylinder Object Freely Resting on the Seabed under the Action of Typhoon
Chongguang Pang*, Liqian Liu
Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao, China
Email: *chgpang@qdio.ac.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 30 April 2014; revised 22 May 2014; accepted 12 June 2014
Abstract
In sandy sediments, scour and fill is the key process contributed to mine burial. The scour processes surrounding the cylinder mines freely resting on the sandy seabed under the 12-hr combined action of tidal currents and wind-generated waves, especially over typhoon events are numerically simulated using the DRAMBUIE model. The East China Sea is a good case study due to the dominant impact of summer typhoon events on sediment transport and scour. The numerical results show that the scour depth generally increases with time under the combined current and wave stresses exerted on the seabed, while the depth of the scour pit depends on infill once the currents subside. There is a positive relationship between the scour depth and the bottom orbital velocity after experiencing 12-hr wave action including storm waves, while the relation is not linear. The experimental results also display an elevated trend for scour depth with the increase of orbital velocity. The numerical results reveal a surprising phenomenon: the mobility of sand altering with the increasing bed shear stress larger than the certain threshold, which is also manifested as the curves of scour depth with the different grain size might cross each other. For laboratory experiments, the variability of sand mobility does not occur, likely because typhoon storm waves cannot be reproduced in the flume. More numerical tests indicate that the intersection will be triggered by the division of critical Shields parameter. The preliminary analysis suggests that the phenomenon never documented is likely generated from the error of empirical formulae.
Keywords:Scour Process, Sediment Grain Size, Bottom Orbital Velocity, Typhoon Events, Variability of Sand Mobility, DRAMBUIE Model

1. Introduction
Bottom mines in shallow water are particularly difficult to find when they are partially or wholly buried. The ability to predict mine burial both for planning and during operations is, therefore, of great importance to the naval forces. Processes known to contribute to mine burial include burial at impact, usually in low-strength muddy sediments, scour and fill in sandy sediments, focused by this paper, bedform migration or transverse bedform movement, liquefaction or fluidization of the sediment, and so on (Wilkens and Richardson, 2007) [1] .
By now there have been some models for predicting the scour burial. Comparing with WISSP (Wave-Induced Spread Sheet Prediction) model, NBURY model (developed in 1980 for German Navy), and Mulhearn model (a model about large migrating bedforms developed by the Australian Defence Science Technology Organization), DRAMBUIE (Defense Research Agency Mine Burial Environment) model can combine tidal current, wave, sediment grain size, water depth and the characteristics of bottom-resting objects better when estimating scour and burial progress, and it is more easily implemented than Vortex-Lattice model (developed by Jenkins and Inman at Scripps) (Friedrichs, 2001) [2] . Moreover it has been verified by in-situ experiments (Elmore and Richardson, 2003) [3] , and been widely used by many researchers (Testik et al., 2007; Guyonic et al., 2007; Cataño-Lopera et al., 2007) [4] -[6] . Therefore, this paper predicts the scour-induced burial of cylinder mine freely resting on seabed in the East China Sea using the DRAMBUIE model.
Most experimental investigations, along with the dimensional analysis, showed that the scour burial depth of the object is primarily a function of the following: the Keulegan-Carpenter (KC) number, the Shields parameter, or both parameters. Other properties that might also play a role are the mean grain size, the density of the sediment and the density of water, the length to diameter ratio of object, and so on (Cataño-Lopera et al. 2007) [6] . In this paper, two primary external parameters determining scour burial characteristic are investigated during the scour process, which are the Shields parameter and mean grain size. In Chinese shelf seas, the dominant forcing from which the Shields parameter is calculated, is comprised of tidal current and wave motion, expressed as bottom orbital velocity. Over long time scales (such as season) the tidal current remains nearly stable, while the bottom orbital velocity changes intensively, particularly during typhoon events. Hence, this paper will explore the bottom orbital velocity under the action of typhoon events, grain size of seabed sand and their impacts on the scour depth surrounding the cylinder mine in the East China Sea using the DRAMBUIE model.
2. The Theory of DRAMBUIE and Its Implementation
DRAMBUIE model was developed to predict the burial of isolated free-settling objects (e.g., cylinder mines) resting on a bed of mobile sandy sediment under the action of waves and tidal currents (Friedrichs, 2001) [2] .
2.1. The Scientific Basis of DRAMBUIE Model
An empirical formula (Whitehouse, 1998) [7] is used to describe the increase in scour pit depth over time about a target located in a steady, unidirectional flow
 , (1)
, (1)
where S¥ is final scour depth as time approaches infinity, and also named as equilibrium scour depth, T is the burial time-scale factor which governs the rate of scour pit growth, P is a fitting coefficient, P = 0.6 for a horizontal cylinder, P = 0.5 for a vertical cylinder.
The value of S¥ is given as a relationship between Shields parameter q¥ and critical Shields parameter qcr in the following manner
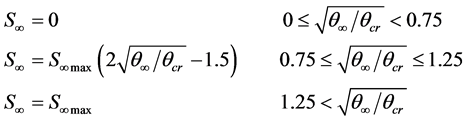 , (2)
, (2)
where 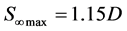 is the maximum depth of scour pit, D is the diameter of cylinder. The presence of cylinder locally speeds up the current velocity via an empirically determined “velocity multiplier”, so the initial grain movement happens when
is the maximum depth of scour pit, D is the diameter of cylinder. The presence of cylinder locally speeds up the current velocity via an empirically determined “velocity multiplier”, so the initial grain movement happens when 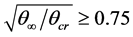 .
.
The critical Shields parameter qcr for initial sediment movement is evaluated empirically to be
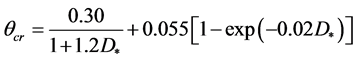 , (3)
, (3)
where  is the dimensionless grain size, n = 10−6 m2/sec, is the kinematic viscosity of water, s is the ratio of sediment density to water (2.65 for siliceous sediment), g is gravitational acceleration, d50 is the median diameter of sediment particles.
is the dimensionless grain size, n = 10−6 m2/sec, is the kinematic viscosity of water, s is the ratio of sediment density to water (2.65 for siliceous sediment), g is gravitational acceleration, d50 is the median diameter of sediment particles.
The another variable T is empirically calculated by the following formula
 ,(4)
,(4)
where A = 0.095 and B = −2.02.
Both S¥ and T contain Shields parameter q¥, so the last unknown variable needed to be solved, is defined as
 ,(5)
,(5)
where t is the total bed shear stress, rs is the density of sediment, 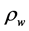 is the density of water at the sediment interface.
is the density of water at the sediment interface.
2.2. Calculating the Total Bed Shear Stress
In this paper, the widely used and well-proven method presented in book by Soulsby (1997) [8] , and being assessed its performance with experiment data by Elmore and Richardson’s paper (Elmore and Richardson, 2003) [3] is chosen to calculate τ. The total shear stress τ is obtained from the stresses induced by wave action, τw, and by currents, τc. The following formulae show their relationship
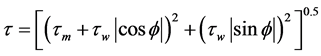 , (6)
, (6)
where f is the angle between the current stress and wave stress vectors, τm is the mean shear stress induced by waves and currents, in the same vector direction as τc
 . (7)
. (7)
 is calculated by the depth-averaged current velocity U, and wave-induced stress
is calculated by the depth-averaged current velocity U, and wave-induced stress ![]() is given by the wave-induced bottom orbital velocity Ub.
is given by the wave-induced bottom orbital velocity Ub.
 is calculated by
is calculated by
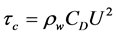 , (8)
, (8)
where U is the depth-averaged current velocity, CD is the drag coefficient calculated by
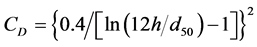 , (9)
, (9)
where h is water depth.
Wave-induced stress τw is calculated by
 , (10)
, (10)
where fw is the wave friction factor
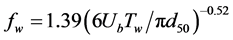 , (11)
, (11)
where Tw is the wave period and Ub is the wave-induced bottom orbital velocity.
2.3. Implement DRAMBUIE Model with MATLAB
The DRAMBUIE model is coded to run on a PC in MATLAB in time-stepped fashion to make it applicable to quasi steady-state conditions. The program is designed to calculate the scour pit depth by inputting current data and wave data at every time step. Here the size of time step is set to be 1 hour for the assumption of quasi-steady state.
Inputs involve the diameter of cylinder D = 0.5 m, water depth h = 30 m, median diameter of sediment d50, depth-averaged tidal current velocity U, wave-induced bottom orbital velocity Ub, and wave period T with time resolution of 1 hour. Outputs include total bed shear stress τ, Shields parameter q¥, final or equilibrium scour pit depth S¥ and scour pit depth S.
d50, depth-averaged tidal current velocity U, wave-induced bottom orbital velocity Ub, and wave period T with time resolution of 1 hour. Outputs include total bed shear stress τ, Shields parameter q¥, final or equilibrium scour pit depth S¥ and scour pit depth S.
Numerical tests have been performed to explore the impacts of grain size and bottom orbital velocity on the scour depth surrounding the cylinder mine freely resting on the seabed. The East China Sea was chosen as an ideal locale for the study. In every summer, the East China Sea is strongly affected by the passage of severe typhoon for several times. Storm-waves and currents associated with the passage of severe typhoon generally cause widespread mobilization of bottom sediments, and rapid scour burial of cylinder mines. In this study, the scour processes impacted by typhoon-induced bottom orbital velocities are manifested using numerical tests. For the DRAMBUIE has only been tested the applicability of cylinder on the fine sand (Elmore and Richardson, 2003) [3] , the range of grain size on the seabed should be restrained in fine and medium sand with the median diameter of 0.05 mm to 0.5 mm, which are dominant sediment types in the East China Sea.
3. Results and Discussion
3.1. Scour Processes Surrounding the Cylinder Mine
The tidal current is assumed as semi-diurnal tide with the fluctuations on the order of 0.4 m/s, which typically occurs in the East China Sea (Wang and Ye, 2007) [9] . The scour processes surrounding the cylinder mines are displayed by several numerical tests with different bottom orbital velocity and grain size.
Figure 1 shows the hydraulic forcing during the 12-hr passage of severe typhoon at the water depth of 30 m, including the tidal current, the orbital velocity induced by winter monsoon of 10 m/s, and typhoon respectively (assuming an outer wind speed of 25 m/s, and a maximum of 35 m/s), in the East China Sea. Wave-induced bottom orbital velocity Ub and its direction a have been numerically simulated by SWAN (Simulating Waves Nearshore) model from http://www.swan.tudelft.nl/. The a is essential for calculating the angle f between the current stress vectors and wave stress vectors. At 30 m, the bottom orbital velocities induced by winter monsoon, outer and maximum typhoon are 0.02, 0.32 and 0.64 m/s respectively.
The scour processes surrounding the cylinder mines freely resting on the sandy seabed under the 12-hr combined action of tidal currents and wind-generated waves at 30 m are illustrated in Figure 2. With the presence of cylinder mines, the combined velocity mostly exceeds the threshold for mobility for the sand sediment due to

Figure 1. The hydrodynamic factors, including tidal current with the fluctuations in solid line, orbital velocity driven by winter monsoon of 10 m/s in solid line with cross marker, orbital velocity induced by 25 m/s outer wind speed of typhoon in solid line with circle marker, orbital velocity generated by 35 m/s maximum wind speed of typhoon in dashed line.
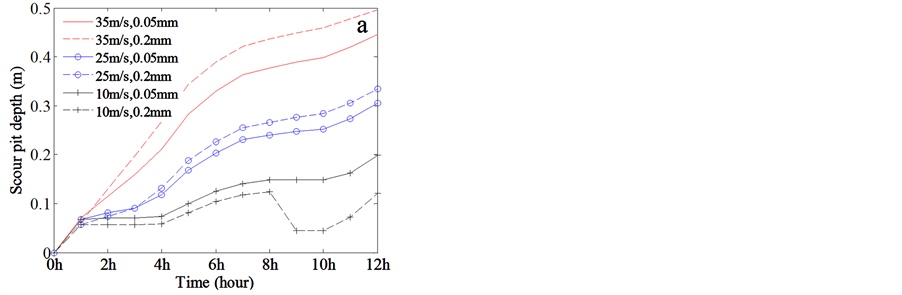
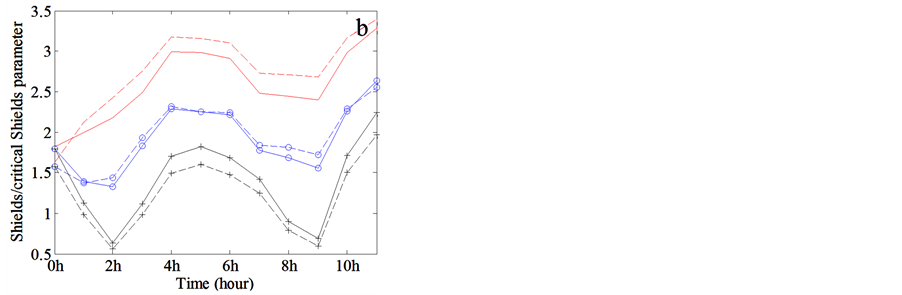

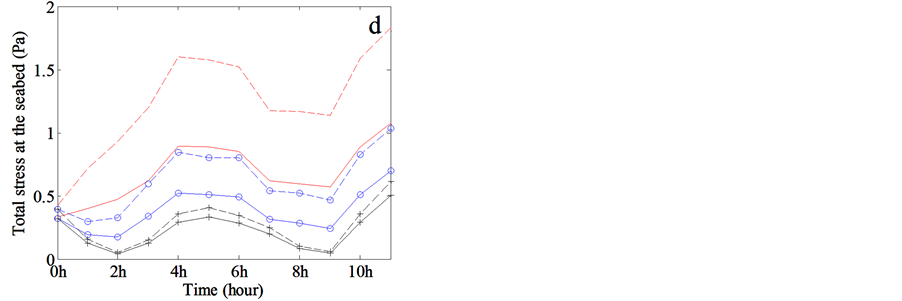
Figure 2. The scour processes surrounding the cylinder mines freely resting on the sandy seabed under the 12-hr combined action of tidal currents and wind-generated waves at 30 m. (a) The scour pit depth; (b) Ratio of Shields to critical Shields parameter; (c) The Shields parameter and (d) Total shear stress exerted on the seabed. The solid line represents very fine sand sediment with median diameter of 0.05 mm, medium sand with median diameter of 0.2 mm shown in dashed line. The line with cross marker denotes the scour process under the wave action generated by 10 m/s wind, the line with circle marker indicates 25 m/s wind-generated wave action, and the line without marker demonstrates the wave action generated by 30 m/s typhoon.
“velocity multiplier”, even if the bottom orbital velocity is very small and can be nearly ignored under the action of winter monsoon. It can be also seen that the shear velocity from the tidal currents alone is regularly above the 3/4 of threshold level to mobilize the sediment. Once mobilized, the sediment will be transported by the mean currents due to both the tides and wind driven flows, and the local scour surrounding the cylinder mines will develop.
The scour pit depth generally increases with time under the combined shear stresses exerted on the seabed even though assuming the infill occurrence. Nevertheless, as soon as the currents subside and the shear velocity decreases down to 3/4 of critical velocity, the sediment would fill the pit, and the infill occurs. For example, at the ninth hour, when the shear velocity created by both tidal current and 10 m/s wind wave action is less than 3/4 of critical value for very fine sand of 0.05 mm, the scour pit depth diminishes due to infill, as shown in dashed line with cross marker of Figure 2(a).
There is a positive relationship between the scour pit depth and the bottom orbital velocity after experiencing 12-hr wave action, while the relation is not linear (Figure 2(a)). At the water depth of 30 m, the depth of scour pit for sand with median diameter of 0.2 mm was 0.12 m, 0.33 m, and 0.49 m respectively, responding to the orbital velocity of 0.02 m/s, 0.32 m/s and 0.64 m/s for winter monsoon, outer wind speed, and maximum speed of typhoon.
The increasing rate of scour depth is not only related to bottom orbital velocity, but also connected with median grain size of sediment on the seabed (Figure 2(a)). That is to say, the depth of scour pit varied with median grain size of sediment even in same dynamic conditions, whereas the difference between variable grain sizes is not significant. Furthermore, the other protruding phenomenon is that the mobility (or erodibility) of sand alters with the increasing bed shear stress mainly produced by the increasing orbital velocity, causing their scour depths to vary simultaneously. As shown in Figure 2(a), the scour depth for very fine sand is all through slightly deeper than that for medium sand under the combined action of tide and 10 m/s winter monsoon, whereas the scour depth for very fine sand is mostly shallower than that for medium sand under the action of 25 m/s or 35 m/s typhoon when the orbital velocity and bed shear stress increase. In addition, the curves of scour evolution with different grain size intersect at the first hour for 35 m/s wind-generated storm, and at the third hour for 25 m/s wind-generated storm. The unique phenomenon will be elucidated as the Section 3.3.
The ratio of Shields to critical Shields parameter, the Shields parameter and total shear stress exerted on the seabed during 12-hr wave actions are illustrated in Figures 2(b)-(d), respectively. Large bottom orbital velocity always produces the corresponding large bed shear stress, accompanying with the bigger stress for coarser grain size. Moreover, the discrepancy between very fine sand and medium sand will enlarge when the orbital velocity is elevated (Figure 2(d)). The Shields parameter changes similarly excepting the smaller value for coarser grain size while the orbital velocity increases, and the Shields curves with different orbital velocity might cross each other (Figure 2(c)). The ratio of Shields to critical Shields parameter follows nearly the same trend as total shear stress, while the difference between two grain sizes alters with the increasing orbital velocity, in other words, the ratio for very fine sand is slightly bigger than medium sand when orbital velocity is small, but the situation is reversed as orbital velocity is largely enhanced, shown in Figure 2(b).
3.2. Laboratory Experiments on Scour Burial
Laboratory experiments on scour burial under the wave action have been performed. However typhoon storms cannot be physically simulated due to the limited capability of laboratory equipments. The flume is supplied with a 20 m long, 0.7 m wide and 0.7 m deep working section. The water depth of working section is 0.3 m. Two basic types of bed sand are used, fine sand with median grain size of 2 - 3φ (0.1 - 0.2 mm) and 0 - 1φ (0.5 - 1.0 mm) coarse sand. The red cylinder model mine with the diameter of 5 cm and length of 22 cm freely rests on the sand bed with two positions of vertical cylinder (case 1) and horizontal cylinder (case 2), as shown in Figure 3. For each basic sand type, 9 sets of wave action are tested. The experiment results are shown in Table 1 for fine sand, including averaged amplitude and near-bottom orbital velocity during wave actions, median grain size and scour depth surrounding cylinder mine after 2-hr wave actions.
The following formulae are obtained by the method of least squares, where r is correlation coefficient. The simple linear fitting are chosen due to the constraint of experimental number.
For case 1 (vertical cylinder), 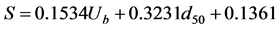 , r = 0.7106;
, r = 0.7106;
For case 2 (horizontal cylinder), 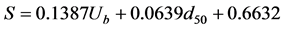 , r = 0.6252.
, r = 0.6252.
The empirical formulae display an elevated trend for scour depth with the increase of orbital velocity and with the reduction of grain size, which the median diameter of grain size reduces when the value in φ unit increases. The experimental results are similar to the above-obtained numerical ones (shown in the previous section), and
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 3. Experimental results on scour burial of cylinder model mine after 2-hr wave actions. Design wave of 17 cm amplitude and 2.0 s period for coarse sand, (a) vertical cylinder and (b) horizontal cylinder; Design wave of 20 cm amplitude and 2.0 s period for fine sand, (c) vertical cylinder and (d) horizontal cylinder.
also similar to those documented studies (e.g., Farhoudi and Shayan, 2014 [10] ). Nevertheless, the variability of sand mobility does not occur, likely because typhoon storm waves cannot be reproduced in the flume. Therefore, the paper will depend on more numerical tests to explore the variability of sand mobility in the following section.
3.3. Variability of Sand Mobility
More numerical tests have been done to verify the distinctive phenomenon, the mobility (or erodibility) of sand varying with the increasing bed shear stress at times, which are displayed in Figure 4. The output parameters involve the scour pit depth (S in Formula (1)), time-scale factor (T in Formula (4)), final scour pit depth as time approaches infinity (S¥ in Formula (2)), ratio of Shields to critical Shields parameter (q¥/qcr in Formula (2), (3)), the Shields parameter (q¥ in Formula (5)) and total shear stress exerted on the seabed (τ in Formula (6)). The water depth is set to be 30 m, and the depth-averaged current velocity is fixed at 0.3 m/s. The bottom orbital velocity ranges from 0.0 m/s to 0.5 m/s. The median grain sizes of sand on the seabed are assumed to be four levels, 0.05 mm, 0.1 mm, 0.2 mm and 0.5 mm.
Around 0.4 m/s combined velocity, the curves of scour depth with different grain size cross each other (Figure 4(a)). The fine sand is easier to be scoured when combined velocity is less than 0.4 m/s, while the situation is reversed, and the coarse sand is more easily mobilized once the velocity exceeds 0.45 m/s. That is to say, the variability of mobility of seabed sand appears to exist.
The time-scale factor and final scour depth for variable grain sizes of seabed sand are manifested in Figure 4(b) and Figure 4(c), from which the scour depth is calculated. Both of them might cross each other with the increasing combined velocity at certain values, 0.36 m/s for time-scale factor, and around 0.4 m/s for final scour
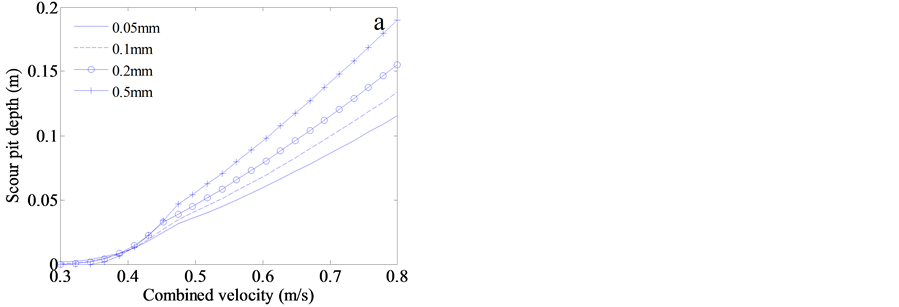
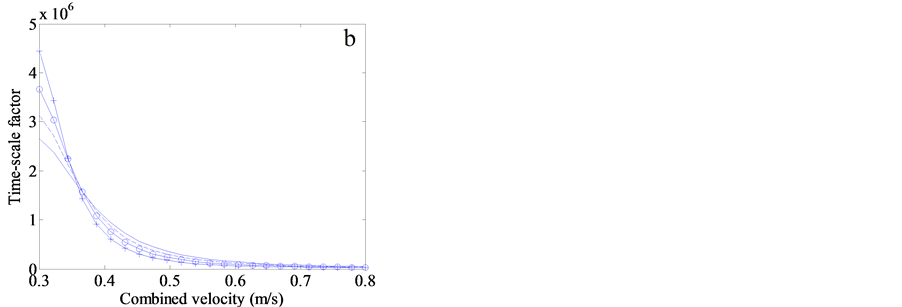
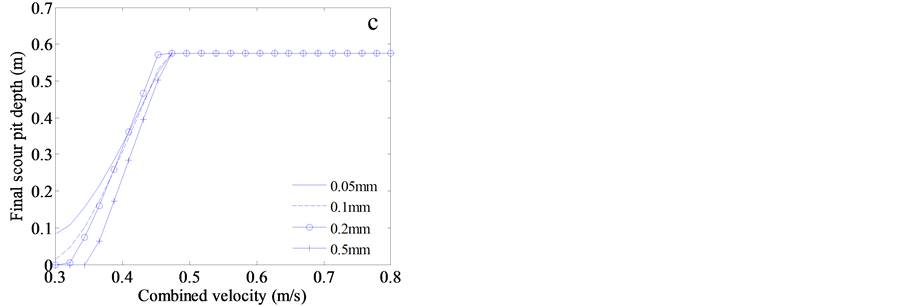
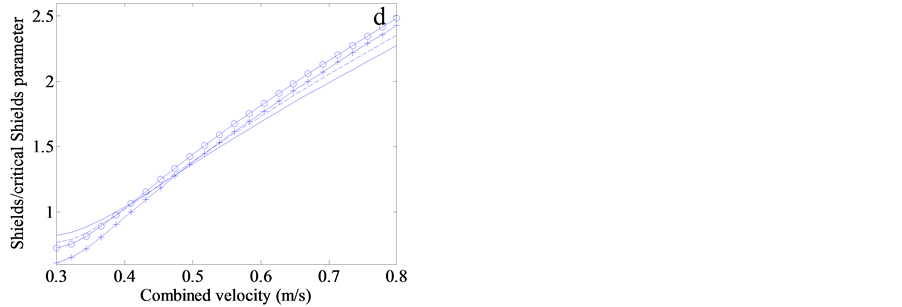
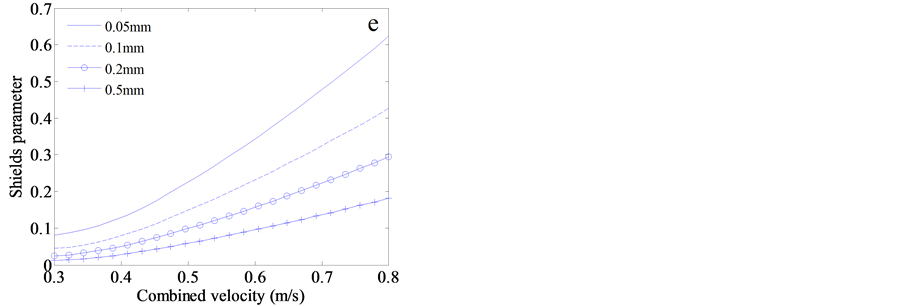
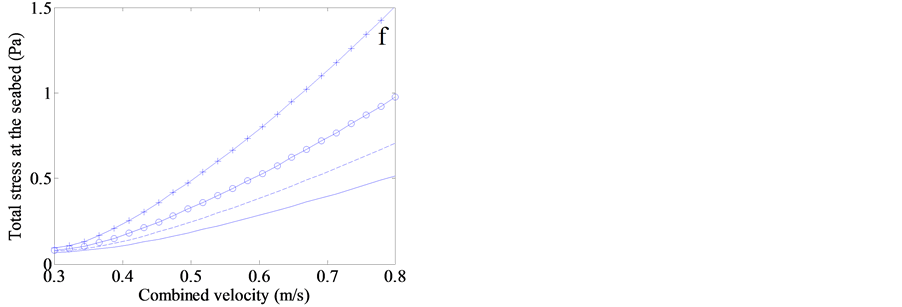
Figure 4. Numerical results about the impact of grain size and bottom orbital velocity on the scour depth surrounding the cylinder mine freely resting on the seabed at 30 m, which is integrated for 1 hr. The depth- averaged current velocity is fixed at 0.3 m/s. The bottom orbital velocity ranges from 0.0 m/s to 0.5 m/s, the combined velocity is only a sum of depth-averaged current velocity and bottom orbital velocity. The median grain size of sand on the seabed is set from 0.05 mm to 0.5 mm. The variables with different grain size change with the increase of bottom orbital velocity, involving (a) the scour pit depth, (b) time-scale factor, (c) final scour pit depth, (d) ratio of Shields to critical Shields parameter, (e) the Shields parameter and (f) total bed shear stress.
depth. However, if investigating the Shields parameter and total shear stress, intersection does not occur (Figure 4(e) and Figure 4(f)). At the same combined bottom velocity, larger total shear stress generally exerts on the coarser sand seabed. With the increasing combined velocity, the difference in total shear stress between very fine sand and medium sand enlarges. At 0.8 m/s, the shear stress exerted on the sandy seabed with median grain size of 0.5 mm is nearly three times larger than that of 0.02 mm median grain size (Figure 4(f)). Nevertheless, for Shields parameter, it is contrary that coarser sand results in smaller Shield parameter, and still no intersection between different grain sizes (Figure 4(e)). When the Shields parameter is divided by the critical value, the intersection will be triggered with the increasing combined bottom velocity, shown in Figure 4(d). More surprisingly, the ratios for 0.05, 0.1, and 0.2 mm median diameter cross each other, while the ratios for 0.2 and 0.5 mm almost remain parallel with the increase of bottom velocity.
The above-mentioned result on the variability of mobility of seabed sand, only calculated from the empirical Formulae (1) to (4) is bewildering, and probably unreal. The previous (e.g., Farhoudi and Shayan, 2014 [10] ) and this paper’s experiments and studies generally demonstrate an increasing trend for maximum scour depth with reduction of grain size due to imposed resistance of larger sized particles, and the trend is irrelevant to the bottom velocity or bed shear stress. The variability of mobility of seabed sand with the increasing bed shear stress has never been documented, and could not be explained reasonably, so that the phenomenon is likely generated from the error of empirical formulae.
However, Sui et al. [11] indicated an interesting conclusion, that when any armor-layer having the same grain size overlies, the equilibrium scour depth of the scour pit will increase with the increase in the particle size of bed material. Hence, in some special circumstances, the scour depth might deepen with the increasing grain size.
More specific designed experiments should be conducted to verify the relationship between scour depth and grain size in various cases, thus an approach and empirical formulae presented by Whitehouse [8] could be improved to conform to experimental results or to eliminate the error by adding a empirical parameter on grain size when the bed shear stress exceeds the cross point.
4. Conclusions
The scour processes surrounding the cylinder mines freely resting on the sandy seabed under the 12-hr combined action of tidal currents and wind-generated waves, especially over typhoon events are numerically simulated using the DRAMBUIE model at 30 m of the East China Sea.
The numerical results show that at the simulated location, the shear velocity from the tidal currents alone is regularly above the 3/4 of threshold level to mobilize the sediment, and the local scour occurs. The scour depth generally increases with time under the combined shear stresses exerted on the seabed including the current and wave stress, excepting that the currents subside and the shear velocity decreases down to 3/4 of critical velocity, the infill will occur. There is a positive relationship between the scour depth and the bottom orbital velocity after experiencing 12-hr wave action including storm waves, while the relation is not linear. The experimental results also display an elevated trend for scour depth with the increase of orbital velocity. The scour depth varies slightly with the median grain size of sediment even in same dynamic conditions. The numerical results also reveal a surprising phenomenon: the mobility of sand altering with the increasing bed shear stress larger than the certain threshold, which is also manifested as the curves of scour depth with the different grain size might cross each other. However, the variability of sand mobility does not occur during our laboratory experiments, likely because typhoon storm waves cannot be reproduced in the flume.
More numerical tests indicate that the intersection will be triggered with the increasing combined bottom velocity when the Shields parameter is divided by the critical Shields parameter. The preliminary analysis suggests that the phenomenon never documented is likely generated from the error of empirical formulae. More specific designed experiments should be conducted to verify the existence of the variability of seabed sand’s mobility.
Acknowledgements
Thanks for the fund of the Major State Basic Research Development Program of China (973 Program) (No. 2012CB956004).
References
- Wilkens, R.H. and Richardson, M.D. (2007) Guest Editorial Special Issue on Mine Burial Processes. IEEE Journal of Oceanic Engineering, 32, 1-2. http://dx.doi.org/10.1109/JOE.2007.890937
- Friedrichs, C.T. (2001) A Review of the Present Knowledge of Mine Burial Processes. http://web.vims.edu/~cfried/reports/2001/Friedrichs2001_ONR_N000140110169_Final_Report.pdf
- Elmore, P.A. and Richardson, M.D. (2003) Assessing Scour Model Performance with Experimental Data. Proceedings of OCEANS 2003, San Diego, 22-26 September 2003, 2350-2354.
- Testik, F.Y., Voropayev, S.I., Fernando, H.J. and Balasubramanian, S. (2007) Mine Burial in the Shoaling Zone: Scaling of Laboratory Results to Oceanic Situations. IEEE Journal of Oceanic Engineering, 32, 204-213.http://dx.doi.org/10.1109/JOE.2007.890970
- Guyonic, S., Mory, M., Wever, T.F., Ardhuin, F. and Garlan, T. (2007) Full-Scale Mine Burial Experiments in Wave and Current Environments and Comparison with Models. IEEE Journal of Oceanic Engineering, 32, 119-132. http://dx.doi.org/10.1109/JOE.2007.890951
- Catano-Lopera, Y.A., Demir, S.T. and García, M.H. (2007) Self-Burial of Short Cylinders under Oscillatory Flows and Combined Waves plus Currents. IEEE Journal of Oceanic Engineering, 32, 191-203. http://dx.doi.org/10.1109/JOE.2007.890968
- Whitehouse, R.J.S. (1998) Scour at Marine Structures: A Manual for Practical Applications. Thomas Telford, London.http://dx.doi.org/10.1680/sams.26551
- Soulsby, R. (1997) Dynamics of Marine Sands: A Manual for Practical Applications. Thomas Telford, London.
- Wang, K. and Ye, D. (2007) Quasi-Harmonic Analysis on One-Day Series Current Data at Three Anchored Stations in the East China Sea. Marine Sciences, 31, 18-25.
- Farhoudi, J. and Shayan, H.K. (2014) Investigation on Local Scour Downstream of Adverse Stilling Basins. Ain Shams Engineering Journal, 5, 361-375. http://dx.doi.org/10.1016/j.asej.2014.01.002
- Sui, J.Y., Afzalimehr, H., Samani, A.K. and Maherani, M. (2010) Clear-Water Scour around Semi-Elliptical Abutments with Armored Beds. International Journal of Sediment Research, 25, 233-244. http://dx.doi.org/10.1016/S1001-6279(10)60041-8
NOTES

*Corresponding author.


