International Journal of Geosciences
Vol.06 No.01(2015), Article ID:53501,8 pages
10.4236/ijg.2015.61003
Dust as a Potential Tracer for the Flow over Topography
Pinhas Alpert, Joseph Barkan
Department of Geosciences, Tel-Aviv University, Tel-Aviv, Israel
Email: pinhas@post.tau.ac.il, yossib@post.tau.ac.il
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 December 2014; accepted 22 January 2015; published 26 January 2015
ABSTRACT
The distribution of mineral dust around topographical obstacles is examined, employing the dimensionless Froude number that describes different flow regimes in a fluid. Flow around a peak with a near-circular shape in a dusty environment like the Sahara and the Sahel was examined in order to investigate the distribution of the dust around the obstacle. The Total Ozone Mapping Spectrometer Aerosol Index (TOMS-AI) daily Aerosol Index, the u and v wind components and the temperature, were used for the period 1979-1992, i.e. 14 years. It is found by the AI data that the shape of the dust distribution around the circular peak is in good agreement with the shape of the peak itself. Additionally good correlation exists between the vertical distribution of the dust above the peak and the Froude Number in its vicinity. This method allows for the first time the investigation of the flow above and around topographical obstacles in different flow conditions in the open space employing dust as the flow tracer.
Keywords:
Dust, Sahara, Froude Number, TOMS, Topographic Flow

1. Introduction and Scientific Background
Extensive research exists about the hydrodynamics of boundary layer flow over complex terrain. The research was made by employing both physical experiments (Chomaz et al., 1992 [1] ) and numerical models (Smolarkiewitz and Rotunno, 1989 [2] 1990 [3] ). Particular effort was made to study the behavior of the flow around and above obstacles (Reisner and Smolarkiewitz, 1994 [4] ; Hughes and Ofosu, 1987 [5] ). It was found that when the Froude number is low, i.e. less than one, the flow regimes are characterized by splitting of the upwind flow (Reisner and Smolarkiewitz, 1994 [4] ).
In recent years, advanced satellite tools have been operated to follow the aerosol distribution over Earth on a daily basis, i.e. MODIS, TOMS-AI, MISR etc. (Dubovik et al., 2008 [6] ; Chin et al., 2004 [7] ; Jaenicke., 1990 [8] ).
The purpose of this preliminary study is to examine the distribution of mineral dust around topographical obstacles in order to identify consistent features that may serve as indicators to the effects of various mountainous obstacles as well as the atmospheric stability on the flow dynamics in their vicinity. For instance, the Froude number (Fr) was often employed as an indicator whether the air-stream will flow above or around the obstacle (Stull, 1988. [9] ). For Fr < 1 air would rather flow around the hill while for Fr > 1 air would flow above the hill. The Froude Number may be defined as
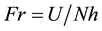 (1)
(1)
where U is the mean wind speed in the air column between the mountain peak and the background; N is the Brunt Vaisala Frequency and h is normally taken equal to the mountain height, dz. The Brunt Vaisala Frequency is defined as:
 (2)
(2)
Hence, for high Fr numbers one would expect to get higher dust concentrations over or near the mountain peak and the opposite for small Fr numbers. Our basic hypothesis would therefore be that a positive relationship exists between the amount of dust over the mountain peak and the Fr number.
In this paper we first present the methodology of our research for a near-circular mountain shape, examine the location of the dust minimum around the peak vicinity and its relation to the Fr number. As mentioned above, this is a preliminary study aimed to examine a relatively simple topographic obstacle with a close to a circular shape.
2. Methodology
2.1. Description of the Topographical Site
In the Gebel Mara massif in Sudan (with a peak of 3000 m ) we choose a mountain with a nearly circular peak, height of 2000 m and the bottom of 1000 m ASL (Figure 1) situated in a dust-rich environment.
The airflow around this topographical shape is investigated with the aid of remotely-sensed observations of dust. The research was made for 14 months of May between 1979-1992, as May is a dust-rich month.
2.2. Description of the Dust Data (TOMS AI) and the Meteorological Data
The Total Ozone Mapping Spectrometer Aerosol Index (TOMS-AI) daily Aerosol Index, the u and v wind components and the temperature, were used for the years 1979-1992, i.e. 14 years. As mentioned above, we used May data. The TOMS-AI daily data were used in order to estimate an index for the total atmospheric column dust amount (Herman et al., 1997 [10] ). This index utilizes the spectral contrast of two ultraviolet channels: 340 nm and 380 nm. It is positive for dust and proportional to the amount of the aerosol in the atmospheric column along the line of sight. The TOMS-AI index is an effective measure for dust mainly at altitudes higher than 1 km , and was shown to be effective in improving dust initialization for dust prediction models (Alpert et al., 2002 [11] ). As far as the reliability of the AI calculation below 1 km is concerned, (Herman et al. 1997 [10] ) indicated that UV-absorbing aerosols in the boundary layer near the ground could not readily be detected by this method. It means that the accuracy of AI is low below 1 km . However, Torres et al. 2002 [12] considered that for mineral dust this restriction for TOMS AI is not so relevant and AI does allow the detection of dust particles even close to the ground. The site we have chosen is above 1 km . Though we are aware about the disadvantage of poor horizontal resolution of the TOMS ( 50 km ) we have to consider the great advantage of the TOMS AI, namely, that due to the very low albedo of the UV particularly over land, it allows a daily noontime dust measurement everywhere, above both land and sea (Prospero et al., 2002 [13] ). It is the only dust-measuring instrument with this capability that is operated since 1979.
The u and v horizontal wind components i.e. wind vectors for the 14 year averages were extracted from the ECMWF 40 year Reanalysis (ERA-40) with resolution of 2.5˚ × 2.5˚, while for the daily data in May 1985 and 1990 (see below) we used the NCEP/NCAR reanalysis (see more details in Section 2.3).
Figure 1. Depiction of the shape of Gebel Mara including the AI isoline in its vicinity with the minimum AI region next to the peak.
2.3. Methodology of the Data Processing
For the peak and its surrounding area a topographical map was prepared (full lines) which contained also the average 14 months isolines of AI (dashed lines) and the 14-month average wind vectors at the mean height of the peak (Figure 2). This height was chosen to be the nearest standard pressure-level, namely 850 hPa, at about the mid-height between the background base and the peak of the mountain, 1 and 2 km respectively.
The AI data were taken from the Giovanni TOMS online visualization and analysis website. The average wind and temperature data is from the ERA-40 reanalysis project and the daily data from the Twentieth century reanalysis (V2) of NCEP/NCAR 1981-2008. The topography was prepared with the Terra program of the US Navy through the GRADS program.
Twentieth century reanalysis (V2) of NCEP/NCAR, 1981-2008, is with 2˚ latitude and 2.5˚ longitude resolution. The AI isolines were created on the basis of the AI data and the AI at the peak and upwind from the peak were determined by these isolines and the wind data.
Figure 1 shows a sketch for the Gebel Mara peak which contains the outline of the mountain (full line), and of the AI isoline (dashed line) in its vicinity with the minimum AI region next to the peak. The minimum AI-dust is found northward to the Gebel Mara peak.
To determine the linkage between the character of the flow around the obstacle and the distribution of the dust over the mountain, several parameters were computed: a) The Froude Number (Fr); b) The Brunt Vaisala
Figure 2. Topography of the Gebel Mara region at the mean height of the peak- 850 hPa (contour full lines, interval 200 m), the AI isolines (dashed lines, interval 0.05), wind vectors at 850 hPa. The AI and the wind averaged for May 1978-1992.
Frequency (N); c) The average AIp at the peak top; d) The average AI upwind from the peak, i.e. the background dust level (AIb). For the areas defined as peak and as background see Table 1.
Where in Equations (1) and (2), g is the gravity; Δθ is the vertical potential temperature difference between the peak and the background;
 is the average potential temperature of the air column between the peak and the background; and Δz is the height difference between the mountain top and the background area. The Froude number definition was given in Equation (1).
is the average potential temperature of the air column between the peak and the background; and Δz is the height difference between the mountain top and the background area. The Froude number definition was given in Equation (1).
The average monthly values for every year of AI on the peak, i.e. AIpeak the, difference between AIpeak and AIb, the Fr number and N for the relevant month (May), were calculated. Correlations were computed as follows: a)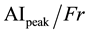 , b)
, b)
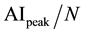 (Table 1). In Figure 3, the scatter diagram of AI on the peak vs. the Froude Number as well as the correlation with the AI at the peak (R = 0.79), is presented.
(Table 1). In Figure 3, the scatter diagram of AI on the peak vs. the Froude Number as well as the correlation with the AI at the peak (R = 0.79), is presented.
Although in high wind events the difference between the peaks and the background tends to diminish and even disappear and consequently the abovementioned correlations will not be relevant, our results show quite high correlations in spite of our averaging approach. In order to examine this assumption about the average results, we prepared daily data in two May months, namely 1985 and 1990 and on the basis of these data computed the daily Froude Number whose values almost in all the 62 days are below 1, suggesting that most of the dust is flowing around the peak and verifying the assumption of the average (Figure 4, Figure 5). Moreover, it can be seen in Figure 6 and Figure 7 that in most of the cases there is more dust at the bottom then on the peak but the Froude number is still less than 1. Note that the cases with more dust on the peak occur when the absolute dust value is high and the stability is relatively low. Presumably, these are border cases, only about 20% from the 62 days.
Another assumption resulting from our averaging approach is that the dust supply is frequent. First of all, the site we are dealing with, is positioned within a sandy desert so there is a high probability that dust in the atmosphere is present most of the time. Second, the strong activity of the wind and the heating of the surface in this desert area cause strong vertical movement that uplift the sand quite often. So there is an unceasing supply of dust presents in the atmosphere and is available around the study site (Israelevich, 2002 [14] ).
Table 1. Gebel mara-details (14 years average).
Fr?Froude Number, N?Brunt Vaisala Frequency, AI?Aerosol Index. All variables measured and computed for May 1978-1992. AI was measured in Gebel Mara and vicinity.
Figure 3. Scatter diagram of the AI on the peak vs. the Froude Number, 14 year average.
Figure 4. Daily froude number?May 1990.
Figure 5. Daily froude number?May 1985.
Figure 6. Daily AI on the top and at the bottom?May 1985.

Figure 7. Daily AI on the top and at the bottom?May 1990.
2.4. The Canary Islands Case
Continuous satellite pictures which were taken above the Eastern Atlantic show a dust wave emanating from the African continent, flowing westward and in its way engulfing the mountainous Canary Islands (Figure 8). These pictures demonstrate so beautifully the effect of the topography on the dust movement.
3. Results
Regarding the relative position of the minimum AI, a clear one in the total column aerosol as expressed by the TOMS-AI is found in the proximity of the mountain peak. This suggests that a definite portion of the dust does not flow above the mountain. Furthermore, the AI isolines generally follow the contours of the obstacle and the minimum AI is shifted towards the north of the peak. The AI based on average of 14 months difference between the peak and the background is shown in Table 1. A good example of this behavior of an entirely different environment in the Canary Islands was provided (see Section 2.4). Examination of the daily data verifies the results of the averaging approach.
There is no clear relation between the average position of the minimum AI and the average wind flow. Presumably the local topography is the dominant factor.
The correlations between AI & Froude Number as well as the AI & Brunt Vaisala Frequency were found high i.e. 0.79 and −0.7 respectively (Table 1). This is as expected since increase in the Fr number should be accompanied by increased AI on the peak, while increase in the atmospheric stability should be accompanied by AI peak reduction.
The distribution of the dust around the circular peak of Gebel Mara in Sudan was examined. The AI data are showing that the shape of the dust distribution around the peak is quite in good agreement with the shape of the peak itself. There exists a reasonably high correlation between the amount of the total column dust above the peak and the Froude Number in its vicinity.
These results suggest that our proposed method may serve as a natural open air laboratory for investigation of flow dynamics over complicated terrain.
Next, we wish to examine with the same methodology different mountain shapes and the relative wind vector
Figure 8. Satellite pictures of dust engulfing the Gran Canary Island.
as well as the other relevant factors i.e. stability (N), amount of background dust, the Coriolis effect in different latitudes, including the Southern Hemisphere.
The present study allows the investigation of the flow deflections over different topographical obstacles and the only limitation is the availability of such in the dusty environments over the Earth.
Acknowledgements
The authors wish to thank L. Gonzales for providing the Meteosat images and Professor D. Tanre for discussions in the very early stage of the paper, both from LOA.
We thank late Y Kaufman for early discussions about this idea.
We acknowledge the ERA40, the NCEP/NCAR reanalysis and the Giovanni TOMS Online Visualize teams whose data enabled this research. We also acknowledge Helmholtz DESERVE project for its support.
References
- Chomaz, J.M., Bonneton, P., Butet, A. and Perrier, M. (1992) Froude Number Dependence of the Flow Separation Line on a Sphere Towed in a Stratified Fluid. Physics of Fluids A, 4, 254-258. http://dx.doi.org/10.1063/1.858353
- Smolarkiewitz, P.K. and Rotunno, R. (1989) Low Froude Number Flow past Three Dimensional Obstacles Part I: Baroclinically Generated Lee Vortices. Journal of the Atmospheric Sciences, 46, 1154-1164. http://dx.doi.org/10.1175/1520-0469(1989)046<1154:LFNFPT>2.0.CO;2
- Smolarkiewitz, P.K. and Rotunno, R. (1990) Low Froude Number Flow past Three Dimensional Obstacles Part II: Flow Reversal Zone. Journal of the Atmospheric Sciences, 47, 1498-1511. http://dx.doi.org/10.1175/1520-0469(1990)047<1498:LFNFPT>2.0.CO;2
- Reisner, J.M. and Smolarkiewitz, P.K. (1994) Thermally Forced Low Froude Number Flow past Three Dimensional Obstacles. Journal of the Atmospheric Sciences, 51, 117-133.
- Hughes, R.L. and Ofosu, K.N. (1987) Froude Number Effects on Flow over Topography. Geophysical & Astrophysical Fluid Dynamics, 38, 177-191. http://dx.doi.org/10.1080/03091928708219203
- Dubovik, O., Lapyonok, T., Kaufman, Y.J., Chin, M., Ginoux, P., Kahn, R.A. and Sinyuk, A. (2008) Retrieving Global Aerosol Sources from Satellites Using Inverse Modeling. Atmospheric Chemistry and Physics, 8, 209-250. http://dx.doi.org/10.5194/acp-8-209-2008
- Chin, M., Chu, A., Levy, R., Remer, L., Kaufman, Y., Holben, B., Eck, T., Ginoux, P. and Gao, Q.X. (2004) Aerosol Distribution in the Northern Hemisphere during ACE-Asia: Results from Global Model, Satellite Observations, and Sun Photometer Measurements. Journal of Geophysical Research-Atmospheres, 109, D23S90. http://dx.doi.org/10.1029/2004JD004829
- Jaenicke, R. (1990) Problems of the Distribution of the Global Aerosol. Russian Chemical Reviews, 59, 959-972. http://dx.doi.org/10.1070/RC1990v059n10ABEH003569
- Stull, R. (1988) An Introduction to Boundary Layer Meteorology. Kluwer Academic Publication, 666 p. http://dx.doi.org/10.1007/978-94-009-3027-8
- Herman, J.R. and Celarier, E. (1997) Earth Surface Reflectivity Climatology at 340-380 nm from TOMS Data. Journal of Geophysical Research, 102, 28003-28011. http://dx.doi.org/10.1029/97JD02074
- Alpert, P., Krichak, S.O., Tsidulko, M., Shapir, H. and Joseph, H. (2002) A Dust Prediction System with TOMS Initialization. Monthly Weather Review, 130, 2335-2345. http://dx.doi.org/10.1175/1520-0493(2002)130<2335:ADPSWT>2.0.CO;2
- Torres, O., Bhartia, P.K., Herman, J.R., Sinyuk, A., Ginoux, P. and Holben, B. (2002) A Long-Term Record of Aerosol Optical Depth from TOMS Observations and Comparison to Aeronet Measurements. Journal of the Atmospheric Sciences, 59, 398-413. http://dx.doi.org/10.1175/1520-0469(2002)059<0398:ALTROA>2.0.CO;2
- Prospero, J.M., Ginoux, P.O., Torres, S., Nicholson, E. and Gill, T.E. (2002) Environmental Characterization of Global Sources of Atmospheric Soil Dust Identified with the NIMBUS 7 Total Ozone Mapping Spectrometer (TOMS) Absorbing Aerosol Product. Reviews of Geophysics, 40, 1002. http://dx.doi.org/10.1029/2000RG000095
- Israelevitch, P.L., Levin, Z., Joseph, J.H. and Ganor, E. (2002) Desert Aerosol Transport in the Mediterranean Regionas Inferred from the TOMS Aerosol Index. Journal of Geophysical Research, 107, 4572. http://dx.doi.org/10.1029/2001JD002011









