International Journal of Geosciences
Vol.4 No.10A(2013), Article ID:41480,10 pages DOI:10.4236/ijg.2013.410A003
Modeling Microbial Decomposition in Real 3D Soil Structures Using Partial Differential Equations
1International Joint Unity (UMI 209) UMMISCO, IRD, Bondy Cedex, France
2INRA, UMR, Environnent and Bigcrops, Thiverval Grignon, France
3School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Vietnam
4Laboratory of Numericalanalysis and Computer Science (LANI), Ummisco UMI 209, IRD, Saint Louis Unit, University Gaston Berger of Saint Louis, Saint-Louis, Senegal
5UMMISCO-Cameroon, International Joint Unity UMMISCO, University of Yaounde 1, Cameroon, IRD (Institut de Recherche pour le Developpement), University of Paris
6CNRS, UMR 7618-Biochemistery and Continenatal Areas Ecology, Thiverval-Grignon, France
Email: jonase@hi.is
Copyright © 2013 Doanh Nguyen-Ngoc et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Doanh Nguyen-Ngoc et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received September 12, 2013; revised October 11, 2013; accepted November 8, 2013
Keywords: Partial Differential Equations; Soil; Microbial Decomposition; Pore Space; 3D Geometry Modelling; Computed Tomography
ABSTRACT
Partial Differential Equations (PDEs) have been already widely used to simulate various complex phenomena in porous media. This paper is one of the first attempts to apply PDEs for simulating in real 3D structures. We apply this scheme to the specific case study of the microbial decomposition of organic matter in soil pore space. We got a 3D geometrical representation of the pore space relating to a network of volume primitives. A mesh of the pore space is then created by using the network. PDEs system is solved by free finite elements solver Freefem3d in the particular mesh. We validate our PDEs model to experimental data with 3D Computed Tomography (CT) images of soil samples. Regarding the current state of art on soil organic matter decay models, our approach allows taking into account precise 3D spatialization of the decomposition process by a pore space geometry description.
1. Introduction
It is a fact that soil structure is a heterogeneous media and organic matter decomposition in soil is one of the most complex ecological processes. The nature of organic matter, the dynamic of microorganisms, the environmental conditions etc. are the major factors which influence the decomposition of organic matter. Despite that microbial dynamics plays an important role in soil organic matter decomposition, the majority of organic matter models make the assumption that carbon limitation is controlled only by the intrinsic degradability of organic matter [1]. There are few models that take into account the rule of exoenzymes produced by microorganisms to convert complex substrates into available compounds [2]. Moreover, most of organic matter models do not consider the physical heterogeneity that controls partly the availability of organic matter to microorganisms [3].
In the recent contributions [4,5], the authors tried to simulate the diffusion of soluble carbon substrate in soil in 2D or 1D. Some attempts were also made to simulate enzyme diffusion in artificial structured environments [6,7]. But none of these models consider explicitly the real 3D soil structure. It is obvious that soil organic matter modeling needs to be in 3D soil structure because 1D or 2D representations of soil structure [8,9] can only supply partial information on the nature of overlapping [10]. Yet the improved performance of 3D X-ray computed tomography sensors now makes it possible to obtain very high resolution images of soil sample volume.
Indeed, such non-destructive imaging technologies (Xray tomography or CAT, laser scanning confocal microscopy or LSCM) can generate digital gray scale images that visualize 3D soil structure at aggregate [11] and also smaller intra-aggregate scale (16 μm in [12]; 3 μm in [13]).
Recently, the new model of Monga et al. in [14] simulated the decomposition of organic matter at a microscale using computer tomography images of real 3D soil but it does not take into account the diffusion process of dissolved organic matters. The main reason is that it costs a lot of time for computing diffusion process in 3D soil structure even with a very strong computer.
In this study we present an organic matter model that focuses on both transformation and diffusion processes in a 3D soil structure. We use Partial Differential Equations (PDEs) in order to simulate biological activity. In fact, models available in literature that simulates the biological activity in porous media use different techniques like cellular automata to simulate biomass growth in biofilms [15], Partial Differential Equations (PDEs) to simulate biomass recycling in fungal colonies [16] and multiagent system to simulate the impact of earthworms on soil structure [17]. In this work, we focus on the PDE method because 1) PDEs have been widely used to simulate various complex phenomena, particularly including transformation and diffusion processes in porous media but few studies have used this approach to biological soil systems; 2) the recently increasing performances of computer PDE solvers make it possible to simulate more and more complex systems.
This paper dealt with the application of PDEs to simulate organic matter degradation in real micro 3D structures and also took the diffusion into account. We tested our method using high resolution 3D CT of real soil images. Our work faces the problem of solving a nonlinear PDE system (reaction-diffusion) in a non-regular 3D mesh.
The paper is organized as follows. Section 2 presents the biological model. Section 3 presents the mathematical model of soil organic matter decay using PDE system. The PDE system is formed by reaction diffusion equations. The approximation of the model weak solutions is found by using a finite element method and a Newton algorithm. In Section 4, we implement the resolution algorithm by using Freefem3d software [18,19]. In Section 5, we present a validation of our PDE model to a experimental result. Section 6 presents a conclusion and some perspectives. Detailed Freefem3d code is given in Appendix.
2. Biological Model
Our aim is to simulate microbial decomposition in a nonregular 3D geometric volume shape defined by pore space. In this case pore space is described by a set of volume primitives [14,20-22]. Therefore, we take as input the following data:
• Geometrical representation of pore space using a network (attributed relational valuated graph) volume primitives [14,20-22].
• Parameters describing the initial spatial distribution of elements involved in biological activity: microbial biomass (MB), fructose (F), solid microbial wastes (SW), decomposed soluble microbial metabolites (DSM), un-decomposed soluble microbial metabolites (UDSM) and inorganic organic matter (CO2).
Thus, we assume that the microbial decomposition process involves six biological elements noted MB, F, SW, DSM, UDSM and CO2. We denote F the amount of fructose which is added into the environment. And we assume that it diffuses through water path to be consumed by microbial biomass (MB) for their maintenance and growth. It is supposed that MB does not move, so we assume that their diffusion coefficient is very small comparing with others. We further assume that the dead MB is transformed into three kinds of organic matters: solid microbial wastes (SWs) which cannot be consumed by MB and cannot diffuse, un-decomposed soluble microbial metabolites (UDSMs) which can diffuse but cannot be consumed by MB, decomposed soluble microbial metabolites (DSMs) which can be consumed again by MB and can diffuse. MB breathes to produce inorganic carbon (CO2) [2]. Figure 1 summarizes the biological process inside one spatial unit. The output of the simulation system for each step time is the precise distribution of biological activity parameters, i.e.: MB density, F density, SW density, DSM density, UDSM density and CO2 density.
Therefore, we provide a kind of animated film showing spatially the evolution of biological characteristics. From these information, we can easily compute the classical global evolution curves: CO2 content, UDSM content, MB content...
3. Presentation of the Model Using PDE
Let  be the domain representing the soil pore space. Let
be the domain representing the soil pore space. Let  be a given time and
be a given time and
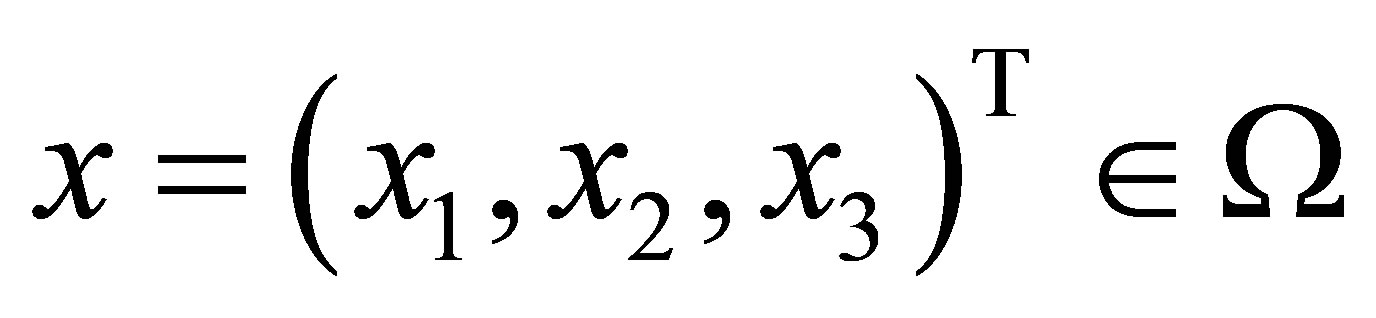 be a point of the pore space. We denote
be a point of the pore space. We denote ,
,  ,
,  ,
, 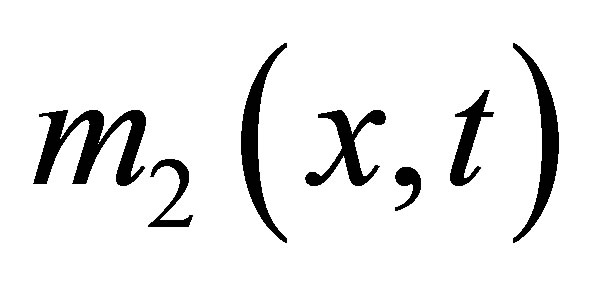 ,
, 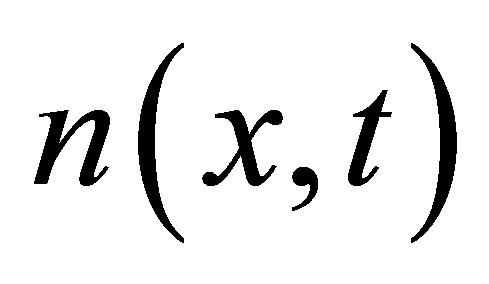 and
and  the densities of microbial (MB), of fructose (F), of solid microbial wastes (SW), of un-decomposed soluble microbial metabolites (UDSM), of decomposed soluble microbial metabolites (DSM) and of inorganic organize matter (CO2) at position
the densities of microbial (MB), of fructose (F), of solid microbial wastes (SW), of un-decomposed soluble microbial metabolites (UDSM), of decomposed soluble microbial metabolites (DSM) and of inorganic organize matter (CO2) at position 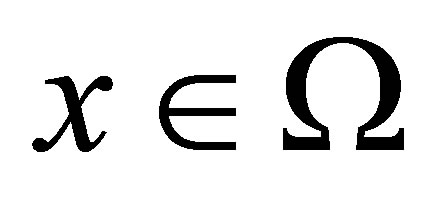 and at time
and at time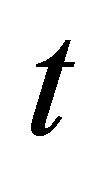 , respectively.
, respectively.
In the next subsections, we presented replicator equations for the variations of quantities of the six biological elements.

Figure 1. Biological processes inside one spatial unit (geometrical primitive).
3.1. Microbial Biomass (MB)
Let  be an elementary volume in
be an elementary volume in . The variation of the quantity of MB in
. The variation of the quantity of MB in  is due to: microbial diffusion, microbial growth, microbial mortality and microbial breathing. Thus during the breathing, microbial decomposers lose a part of their masses. The following equation summarizes the process:
is due to: microbial diffusion, microbial growth, microbial mortality and microbial breathing. Thus during the breathing, microbial decomposers lose a part of their masses. The following equation summarizes the process:

We assume that the MB growth depends on the quantities of fructose (F) and of decomposed soluble microbial metabolites (DSMs). We also assume that microbial consumes F and DSMs according to the Monod equation, proposed in J.D. Murray’s book [23], as follows:
 (1)
(1)
where the variables are set as follows. b is the concentration of microbial decomposers, k is the maximal growth rate,  is the half-saturation constant, f is the concentration of fructose, n is the concentration of decomposed soluble microbial metabolites.
is the half-saturation constant, f is the concentration of fructose, n is the concentration of decomposed soluble microbial metabolites.
The above equation describes microbial decomposers growth rate.Thus, the variation of b is expressed by the following equation:
 (2)
(2)
where  is the diffusion operator,
is the diffusion operator,  represents the microbial decomposers diffusion coefficient,
represents the microbial decomposers diffusion coefficient, 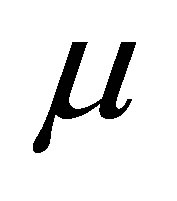 is set to the mortality rate,
is set to the mortality rate, 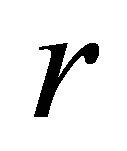 is set to the breathing rate.
is set to the breathing rate.
3.2. Fructose (F)
F density variation comes from: F diffusion and consumption of F by microbial decomposers. Thus, the following equation summarizes F density variation process:

F variation is ruled by the following equation:
 (3)
(3)
where  is the diffusion operator,
is the diffusion operator, 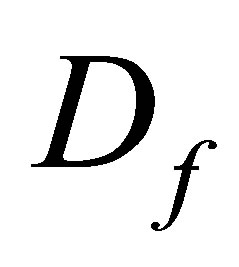 represents the F diffusion coefficient.
represents the F diffusion coefficient.
3.3. Solid Microbial Wastes (SWs)
SW quantity variation comes from the transformation of a part of MB mortality.

Thus SW quantity variation is expressed by the following equation:
 (4)
(4)
where 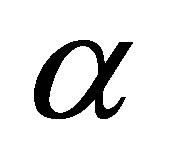
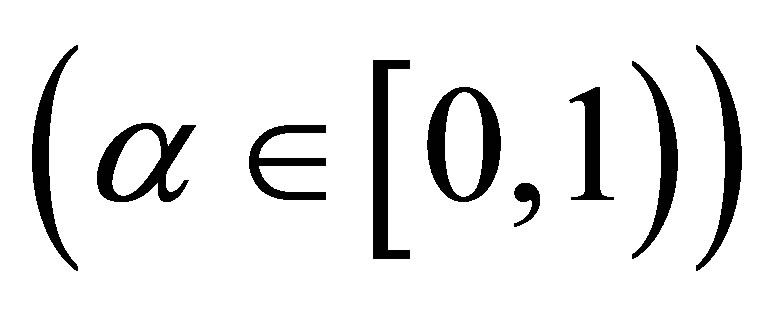 is the rate of dead MB transformed into SW.
is the rate of dead MB transformed into SW.
3.4. Undecomposed Soluble Microbial Metabolites (UDSM)
UDSM quantity variation is caused by the transformation of a part of MB mortality and the diffusion process as follows:
UDSM quantity variation is expressed by the following equation:
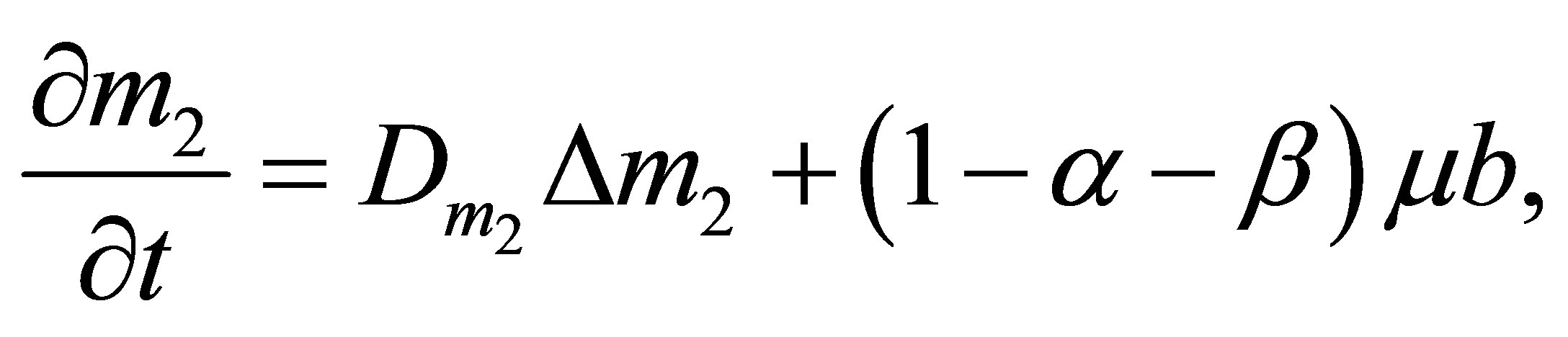 (5)
(5)
where  is the diffusion operator,
is the diffusion operator, 
 is the rate of dead MB transformed into UDSM.
is the rate of dead MB transformed into UDSM.
3.5. Decomposed Soluble Microbial Metabolites (DSM)
DSM density variation comes from: DSM diffusion, a part of dead MB and consumption of DSM by microbial decomposers. Thus, the following equation summarizes DSM density variation process:

DSM variation is ruled by the following equation:
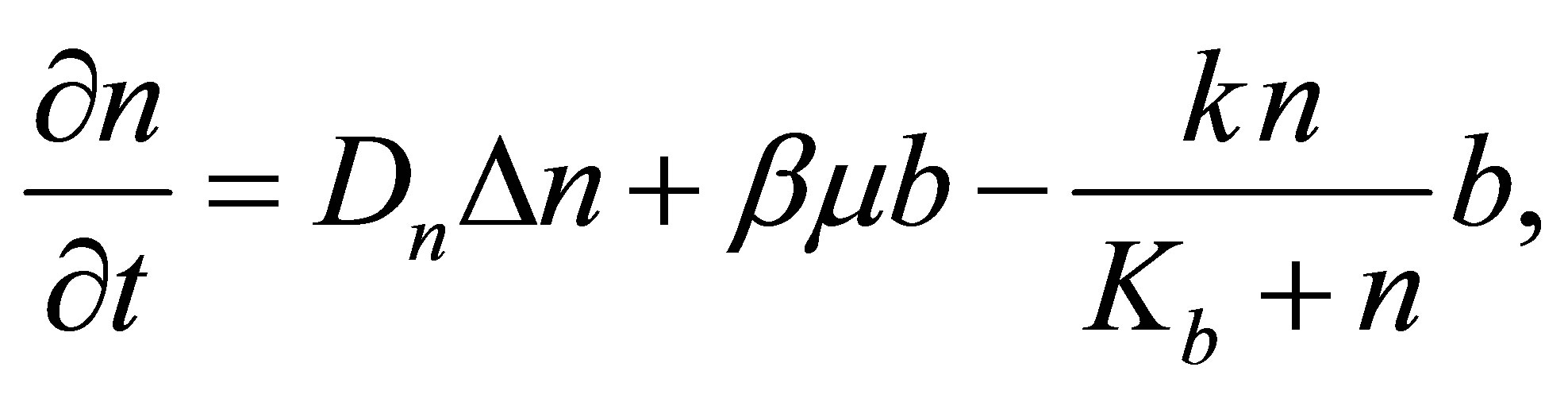 (6)
(6)
where Δ is the diffusion operator,  represents DSM diffusion coefficient and
represents DSM diffusion coefficient and 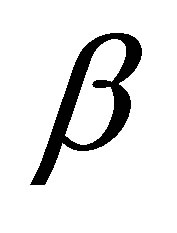 is the rate of dead MB transformed into DSM.
is the rate of dead MB transformed into DSM.
3.6. Inorganic Carbon (CO2)
Inorganic carbon (CO2) variation is due to its diffusion and to its production by microbial decomposers (MB) during breathing.

The CO2 dynamics equation reads as follows:
 (7)
(7)
where  is the diffusion operator,
is the diffusion operator, 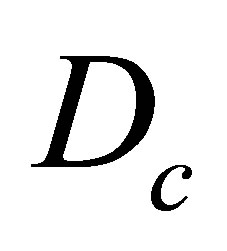 is set to the CO2 diffusion coefficient.
is set to the CO2 diffusion coefficient.
3.7. Boundary Conditions
We assume that biological activities act only insde  and there is not any outside forces that effect on the dynamics inside
and there is not any outside forces that effect on the dynamics inside . It means that flow is null on
. It means that flow is null on 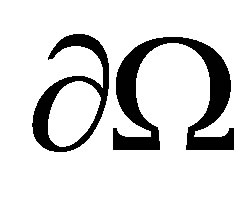 for all variables. Therefore, on the border of
for all variables. Therefore, on the border of  noted
noted , we use the Neumann boundary conditions.
, we use the Neumann boundary conditions.
3.8. The Complete PDE System
In this section we use the above equations describing variable variations to set a global PDE system modeling biological dynamics. Let 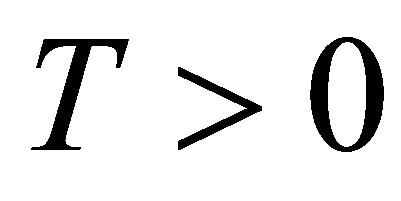 be a fixed time and let’s define
be a fixed time and let’s define
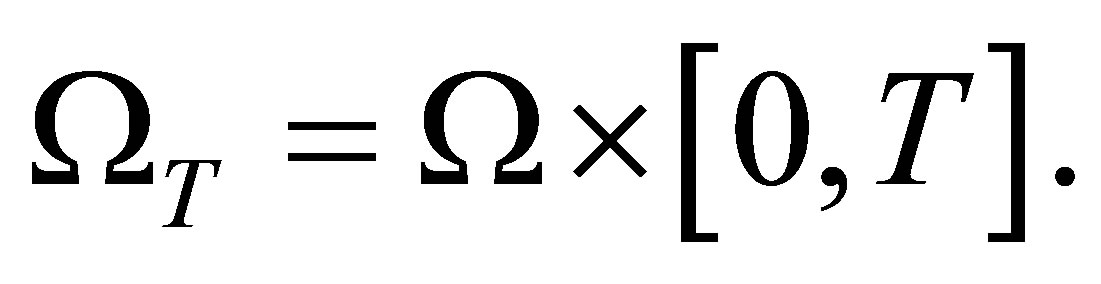 (8)
(8)
Therefore, the whole system of partial differential equations governing the biological model becomes in :
:
 (9)
(9)
 (10)
(10)
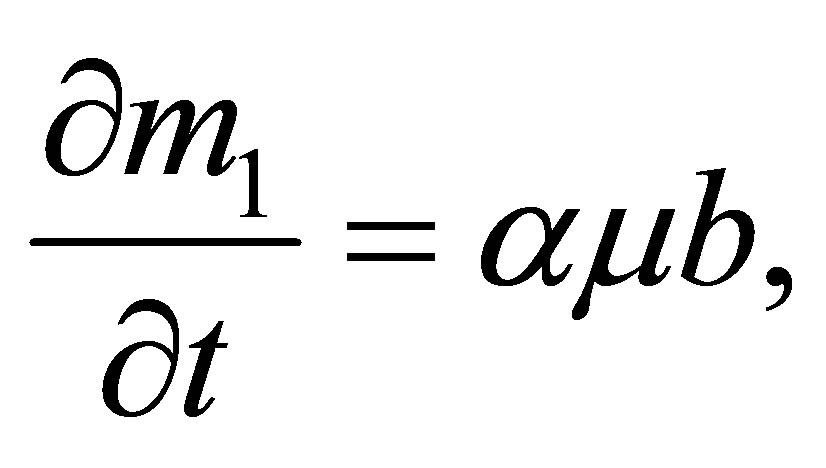 (11)
(11)
 (12)
(12)
 (13)
(13)
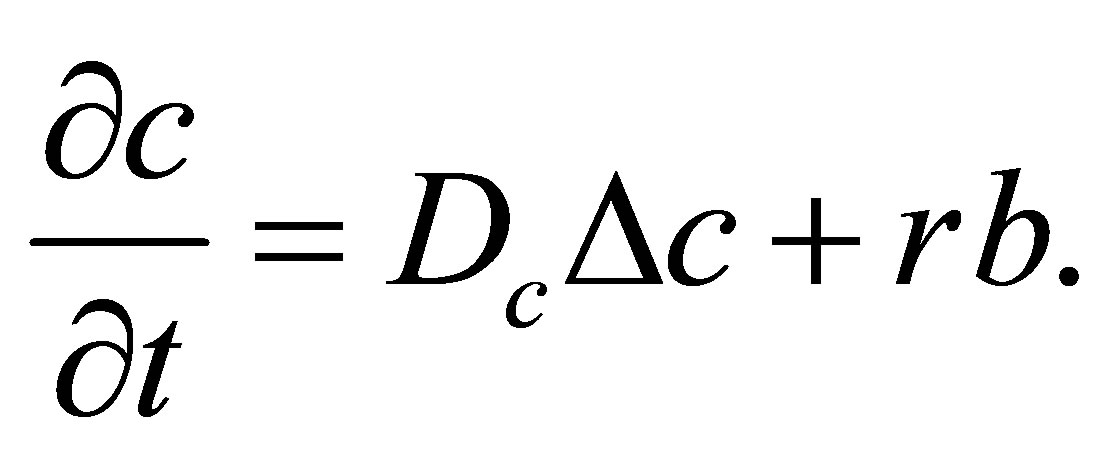 (14)
(14)
We use Neumann homogeneous boundary conditions and the following initial conditions in Ω: 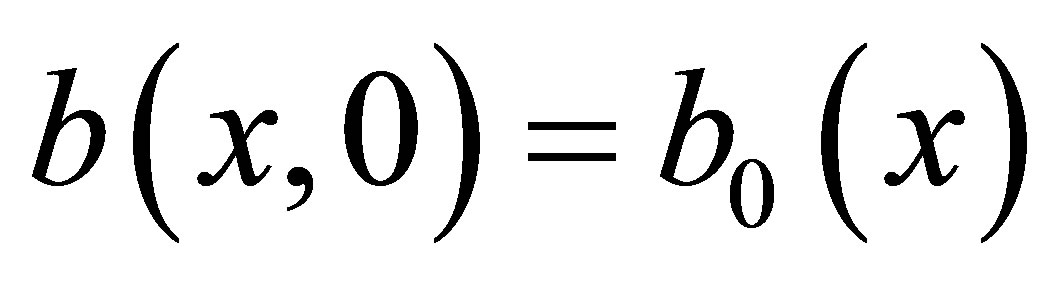 for MB,
for MB, 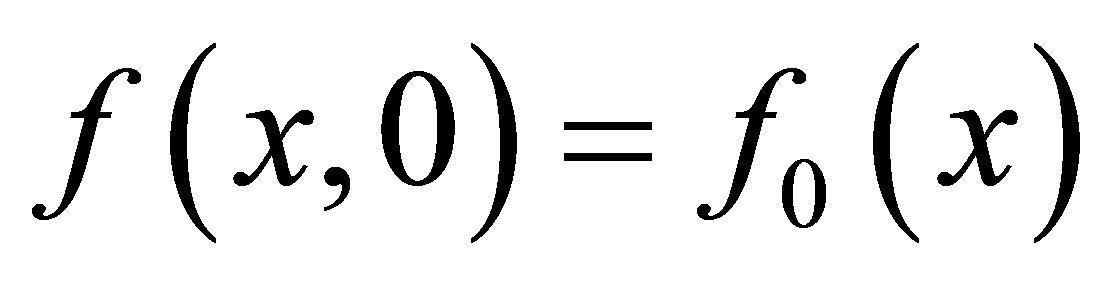 for F,
for F, 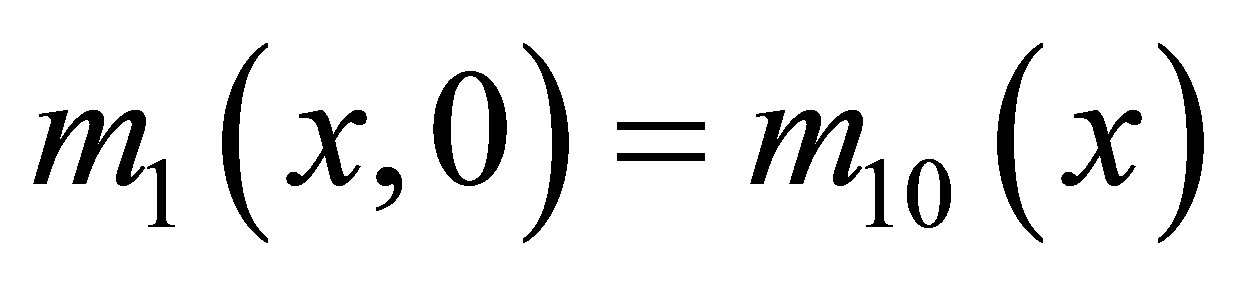 for SW,
for SW, 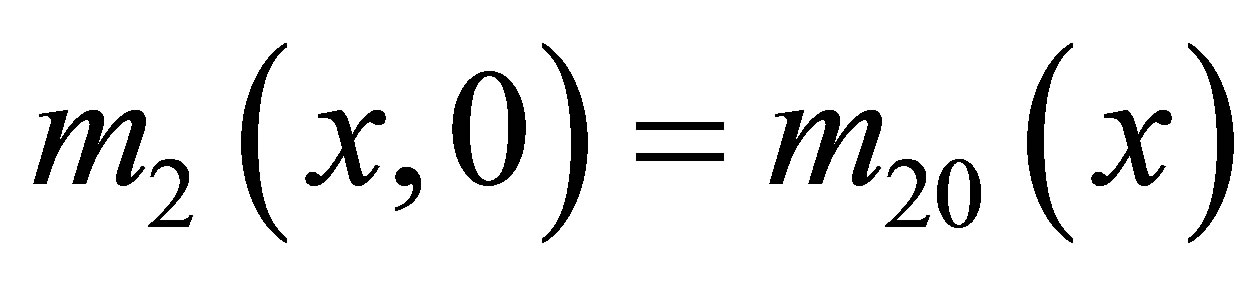 for UDSM,
for UDSM, 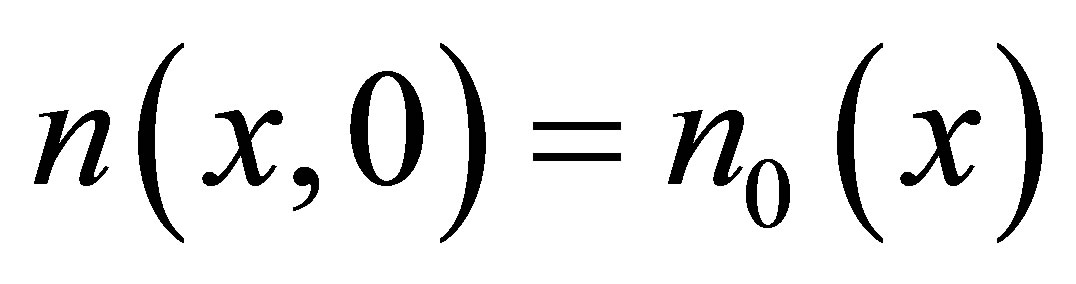 for DSM and
for DSM and 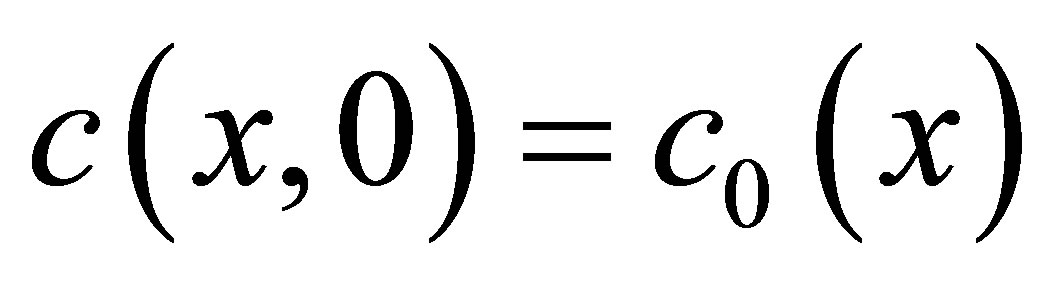 for CO2. The intitial conditions are given by the functions of position
for CO2. The intitial conditions are given by the functions of position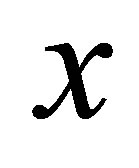 , i.e. amount of the biological elements at the beginning are known at any position in
, i.e. amount of the biological elements at the beginning are known at any position in .
.
Therefore, the above PDE system describes precisely microbial decomposition of organic matter in soil. In the following section, we show how to solve this PDE system which can practically simulate soil biological activity.
4. Numerical Solution of the Complete PDE Model
4.1. PDE Vectorial System Formulation
We simplify the system writing by transforming it into a vector form. Let’s define vectors in the following way:
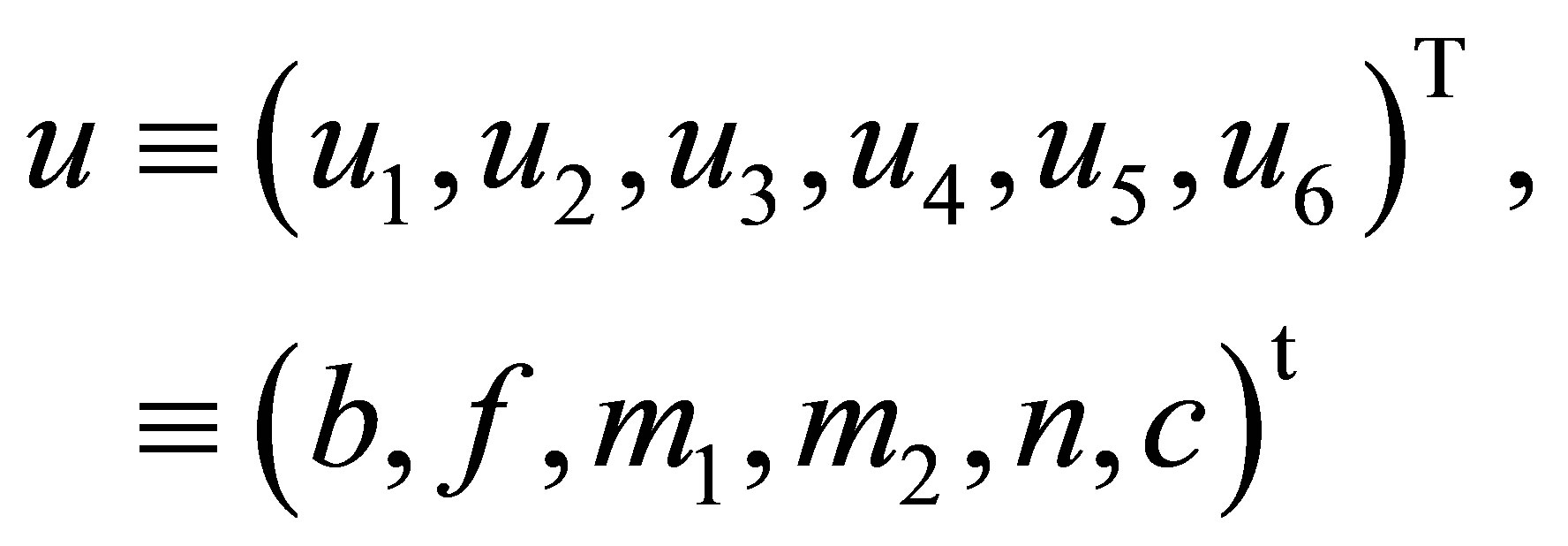 (15)
(15)
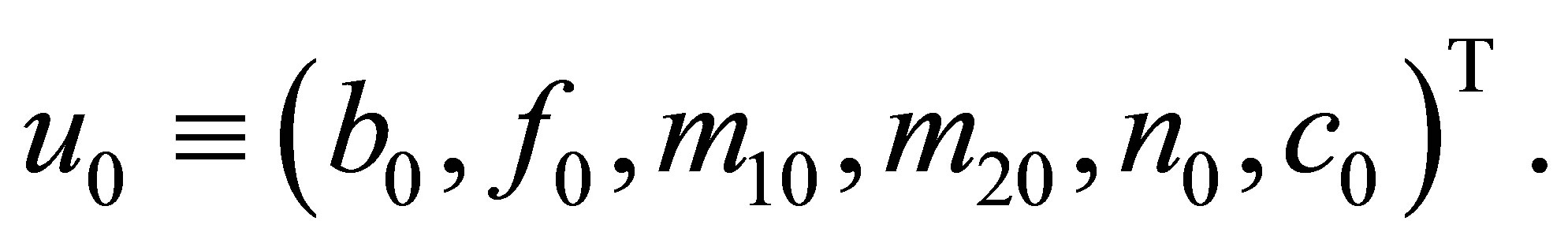 (16)
(16)
The diffusion coefficients matrix  is defined as follows:
is defined as follows:
 (17)
(17)
The reaction terms of equations are represented by functions  defined as follows:
defined as follows:
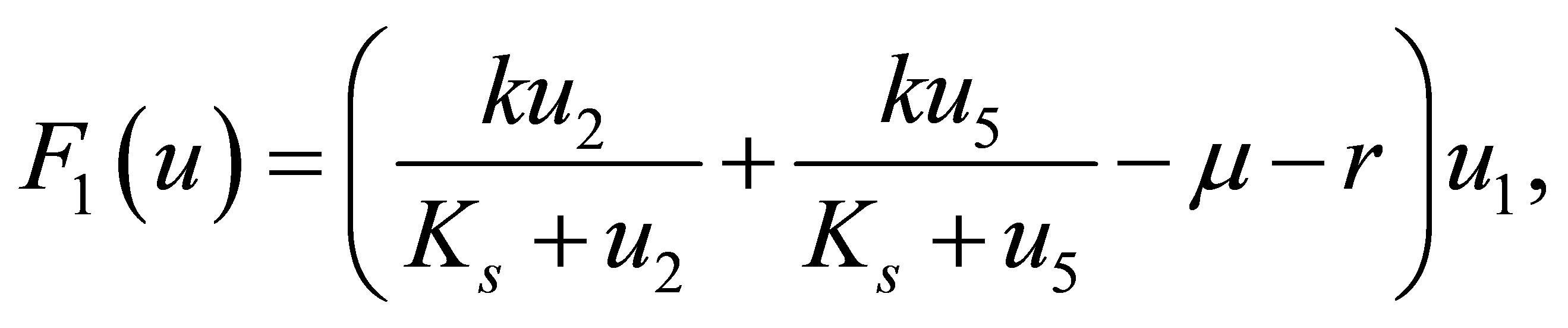 (18)
(18)
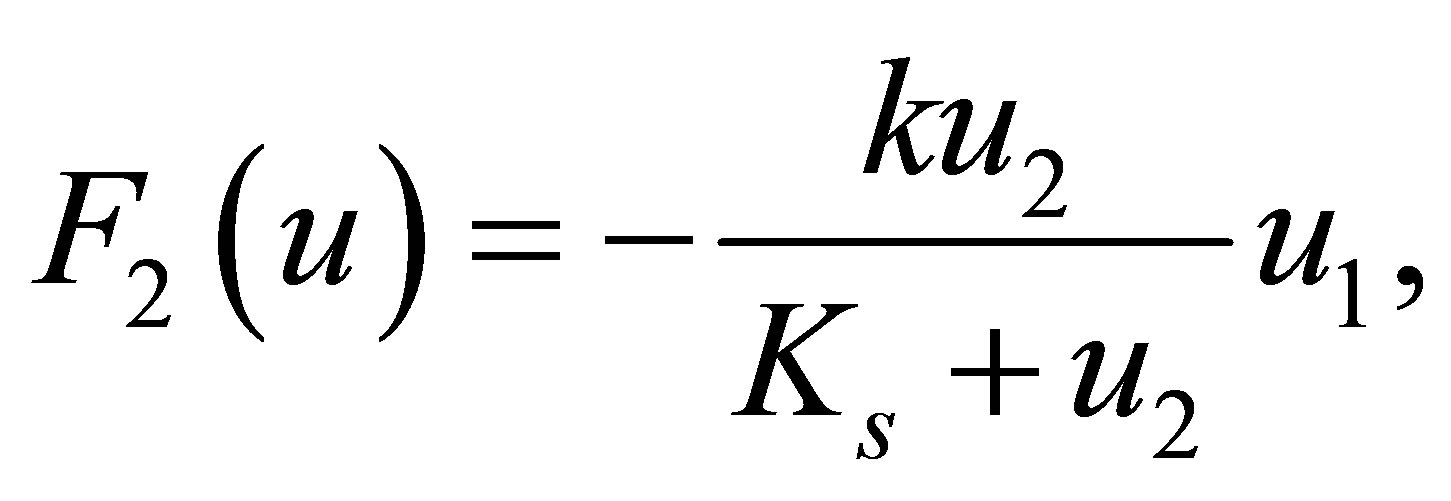 (19)
(19)
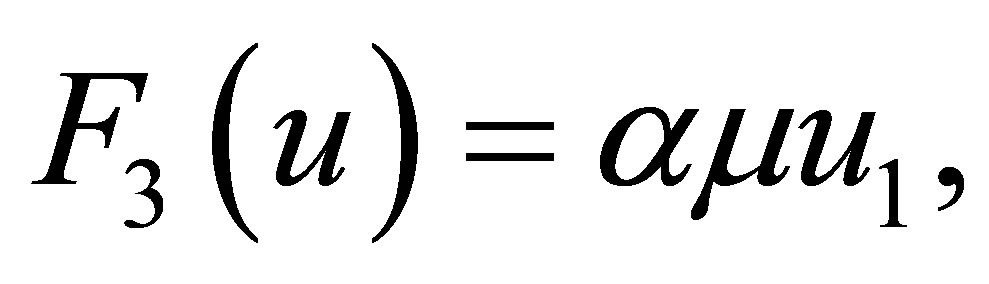 (20)
(20)
 (21)
(21)
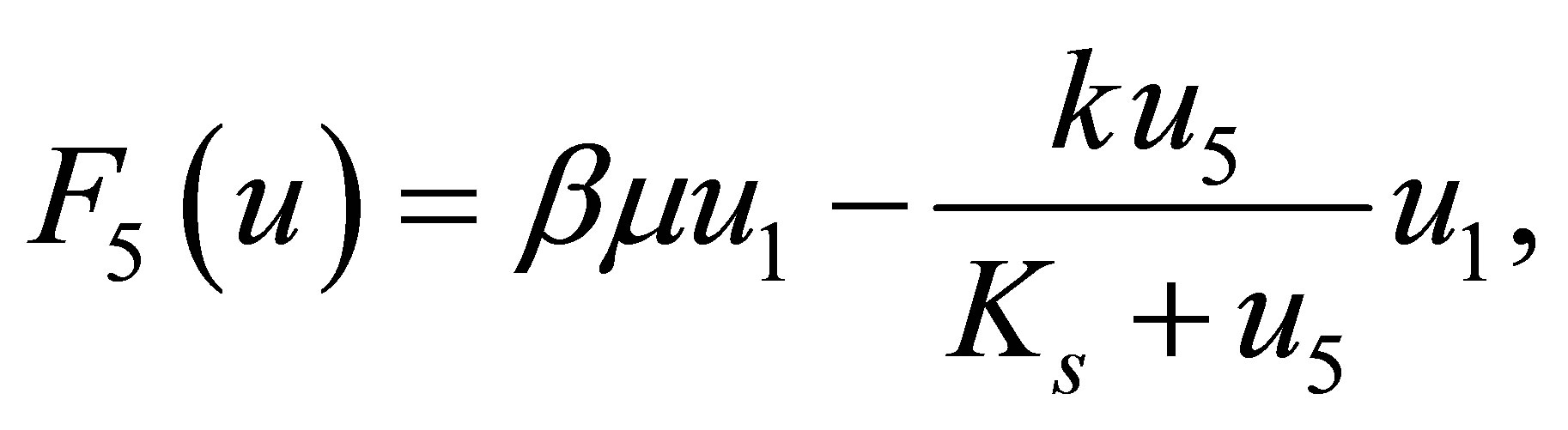 (22)
(22)
 (23)
(23)
Let’s define the vector function  such that
such that
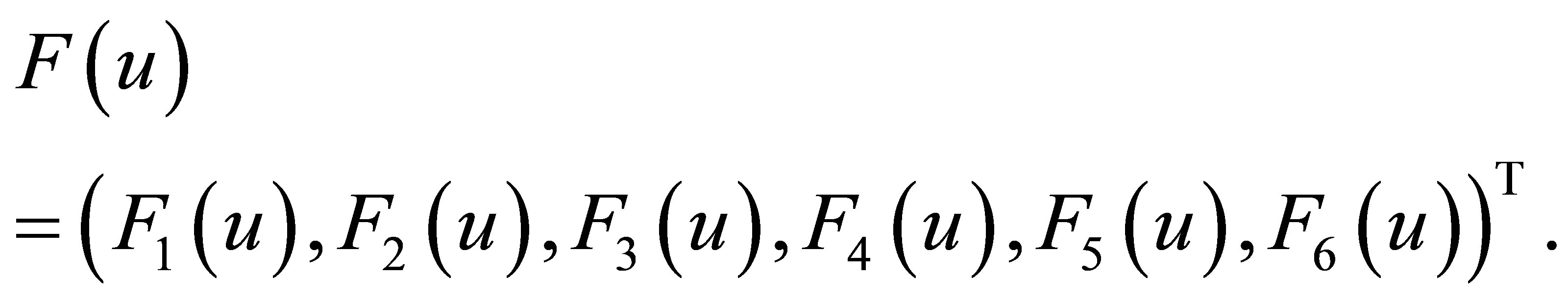 (24)
(24)
The vector form of the system is
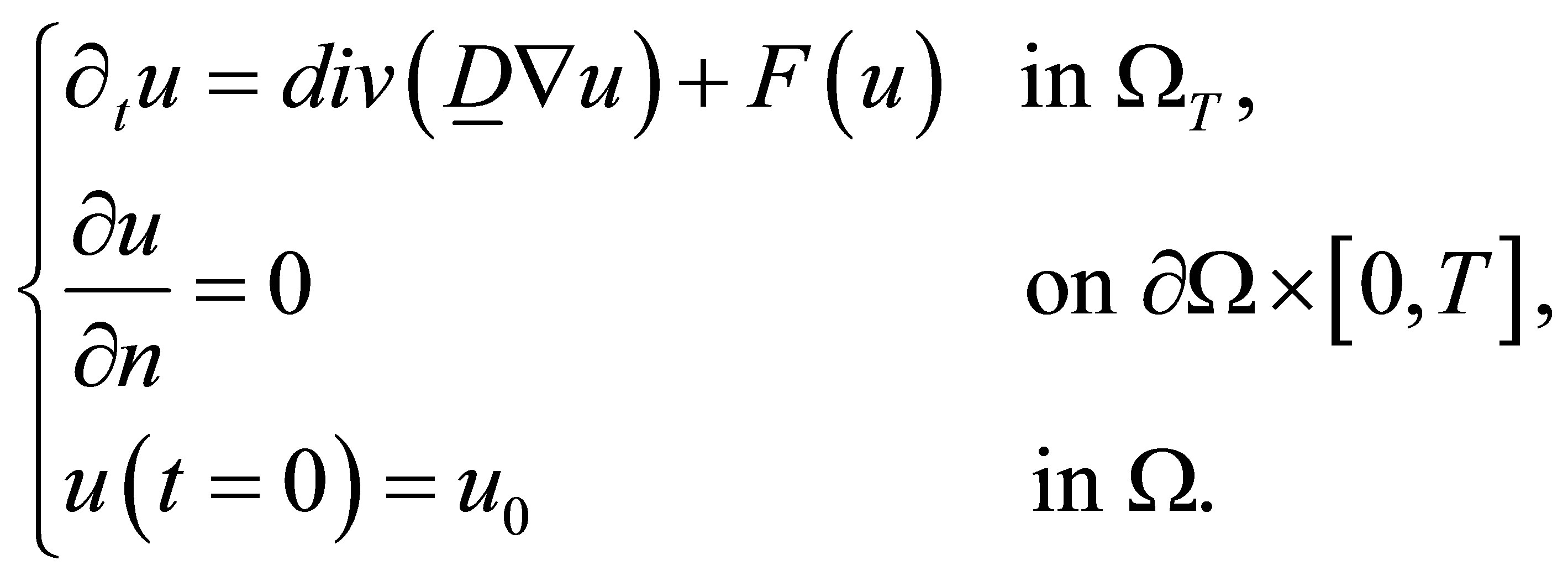 (25)
(25)
4.2. System Variational Formulation
Let’s introduce the following Sobolev space
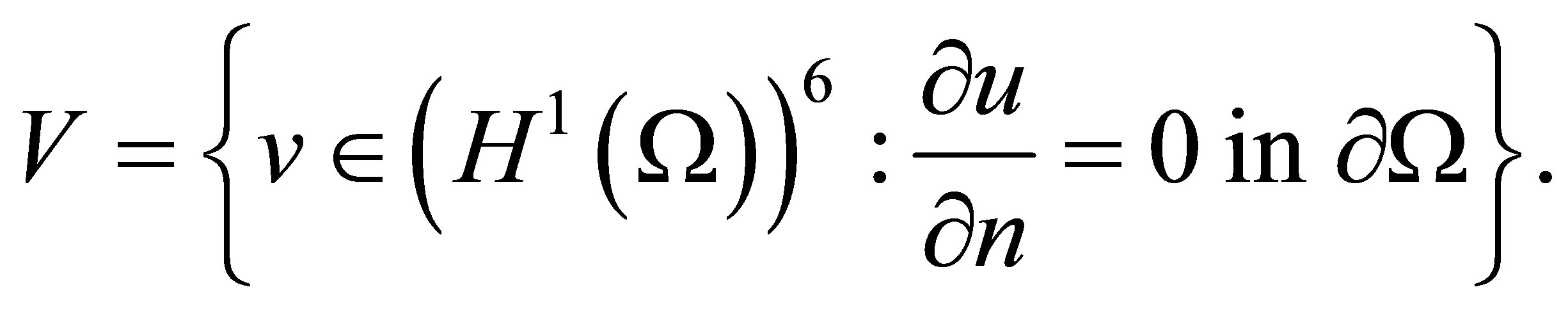 (26)
(26)
Assuming that data are sufficiently regular, the variational formulation consists in finding a function 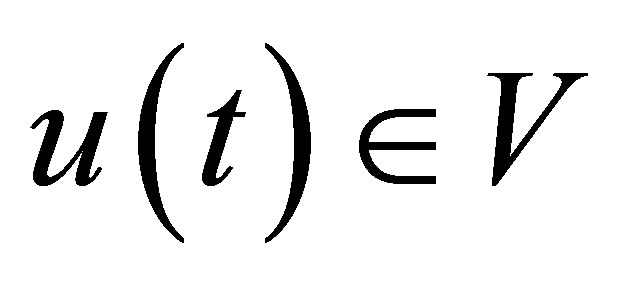 such that:
such that:
 (27)
(27)
4.3. Resolution Scheme of the Variational System
4.3.1. Building a Mesh  of Domain
of Domain 
A mesh of pore space  can be built from a geometrical representation of pore space [14,20-22]. The following algorithm can then be use to build a mesh:
can be built from a geometrical representation of pore space [14,20-22]. The following algorithm can then be use to build a mesh:
• Computing the geometrical primitives network representing pore space We follow the approach described in [14,20-22]. In detail, we compute an adjacency graph representing pore space using 3D computed tomography image of a soil sample. Geometrical primitives can be chose, for instance, the balls as in [12]. Therefore, we obtain an adjacency graph of balls describing pore space where each node is attached to a ball representing a pore within common sense [14,20-22].
• Building a mesh by using all centers of the balls From all centers of the balls, we build a tetrahedra mesh for . In order to do that, we propose using the Delaunay triangulation program developed at INRIA by the GAMMA project [24,25].
. In order to do that, we propose using the Delaunay triangulation program developed at INRIA by the GAMMA project [24,25].
Building the mesh following this way is exactly the same idea as in [14,22] where the transformation process acts inside each ball and the diffusion process acts between the connected balls. Instead of the geometrical modelling approach using updating graph in [14,22], here we consider in this work the mathamatical modelling approach. We are trying to use the benefits of the approach in order to better model biological activities.
• Pruning the mesh We do pruning the mesh in order to neglect edges between two centers of balls that do not connect. Now we get a mesh 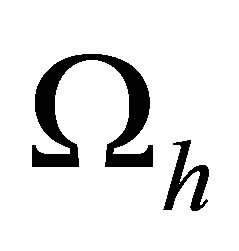 of domain
of domain .
.
After building a mesh  of domain
of domain , we solve the variational formulation (27) in the following discrete space:
, we solve the variational formulation (27) in the following discrete space:
 (28)
(28)
4.3.2. Numerical Scheme
The numerical resolution of the problem is divided into three steps:
• Step 1: We discretize the problem via finite element method in the finite dimensional space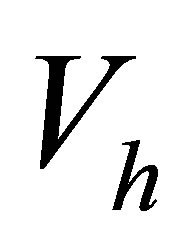 . The problem consists in solving the following system
. The problem consists in solving the following system
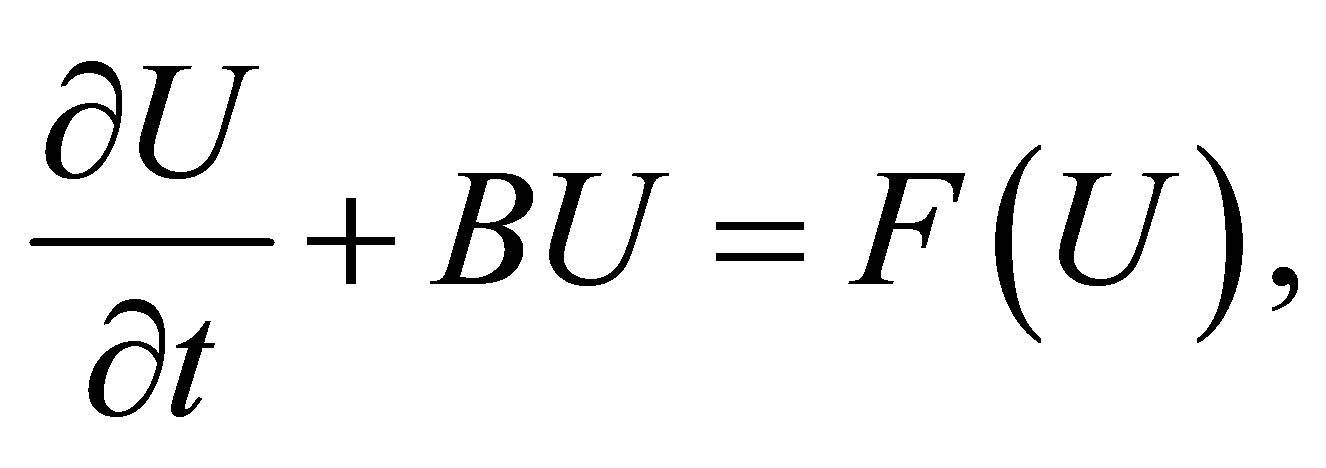 (29)
(29)
where
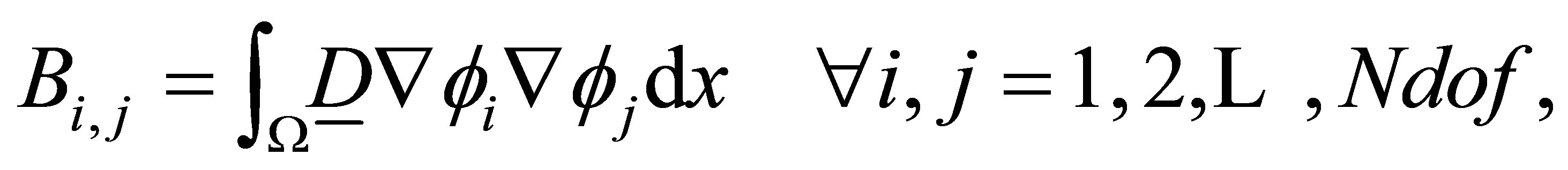 (30)
(30)
and
 (31)
(31)
where 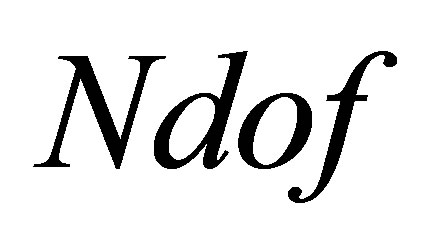 is the number of freedom degrees. The sequence
is the number of freedom degrees. The sequence  defines the basis functions of the space
defines the basis functions of the space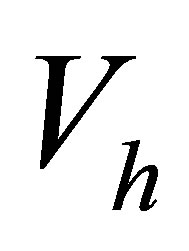 .
.
• Step 2: We use implicit scheme to discretize time.
Let  be a positive integer denoting the number of time steps.
be a positive integer denoting the number of time steps.
We call the step time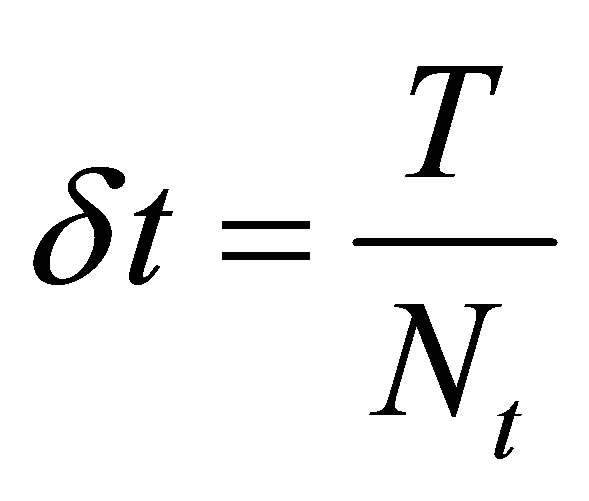 .
.
The numerical scheme is:
 (32)
(32)
which can be as follows:
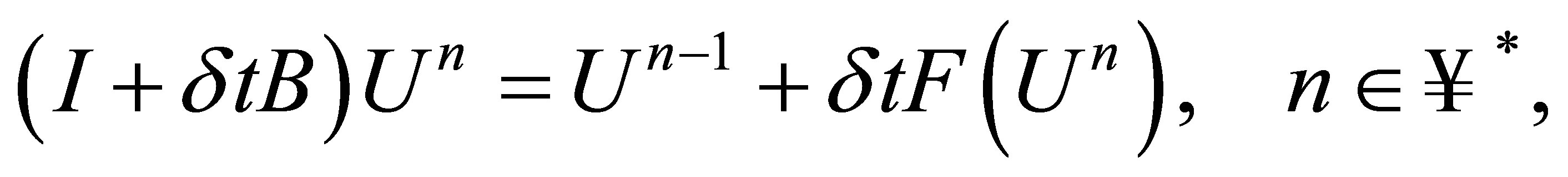 (33)
(33)
where 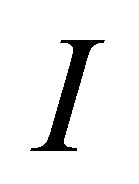 is the identity matrix,
is the identity matrix, 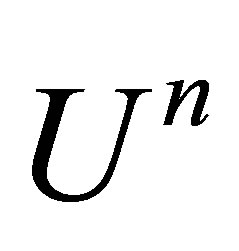 is the solution at time
is the solution at time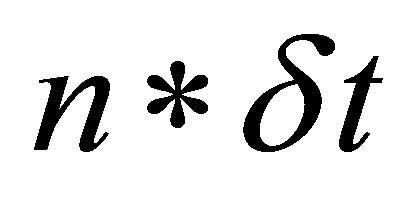 .
.
• Step 3: We linearize the function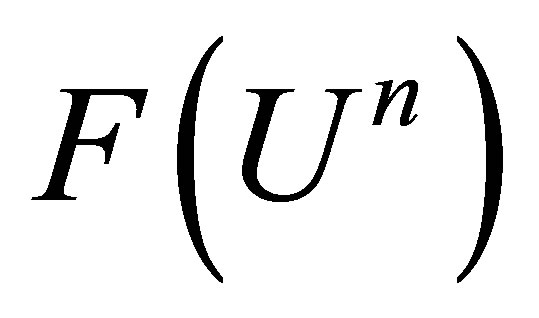 . We ignore
. We ignore 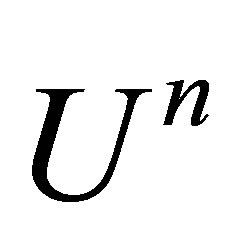 at the time
at the time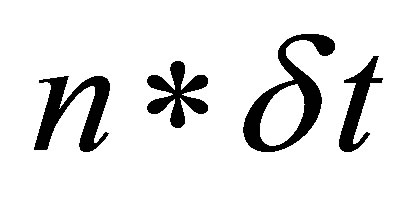 . Therefore, we note
. Therefore, we note 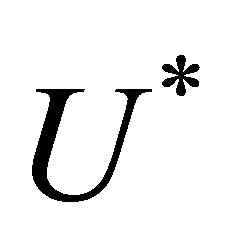 the approximation of
the approximation of 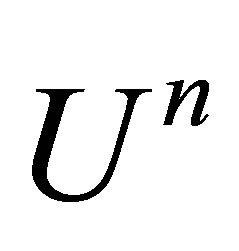 and
and  the correction term. We obtain:
the correction term. We obtain:
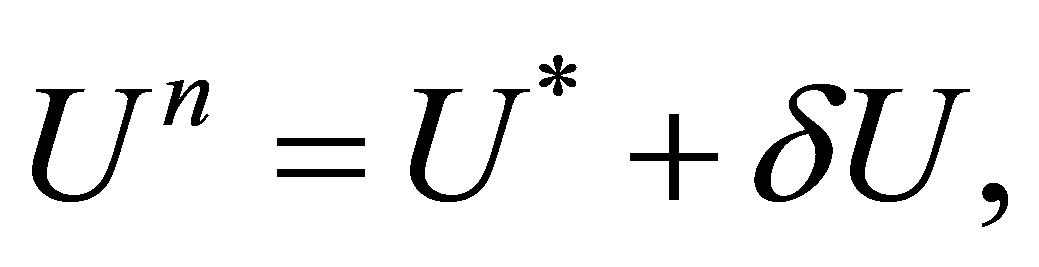 (34)
(34)
so the numerical scheme becomes:
 (35)
(35)
We consider the following approximation:
 (36)
(36)
The numerical scheme becomes:
 (37)
(37)
4.3.3. Resolution Algorithm
From the initial conditions, we know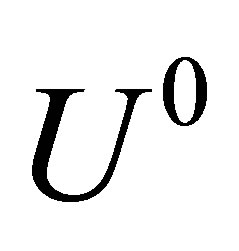 . Then in order to find solution
. Then in order to find solution 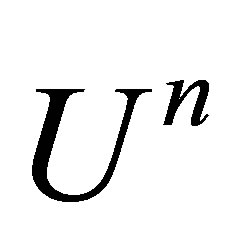 knowing
knowing , we initialize
, we initialize  to
to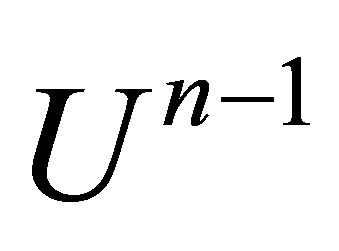 . Afterwards, we repeat the numerical scheme by replacing the term
. Afterwards, we repeat the numerical scheme by replacing the term  by
by 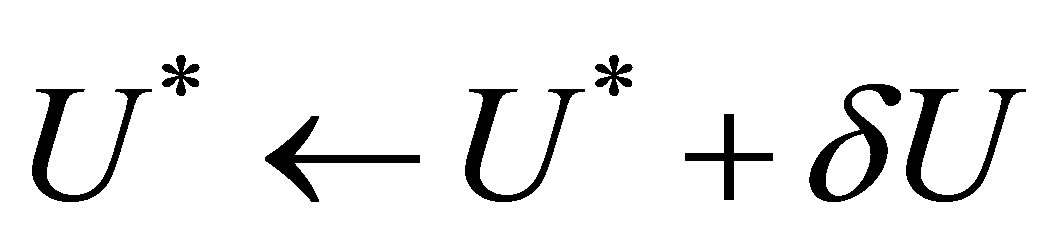 after each iteration. Two stopping criteria are defined:
after each iteration. Two stopping criteria are defined:
• we define a maximal number of iterations called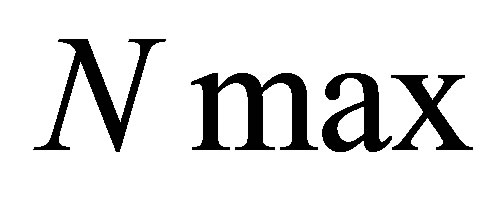 ;
;
• we define a very small positive real  and we stop the loop if the norm of
and we stop the loop if the norm of 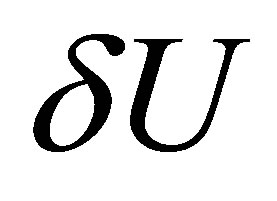 is smaller than
is smaller than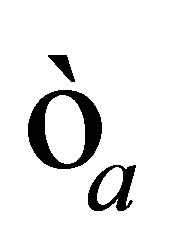 .
.
When one of the stopping criteria is satisfied, 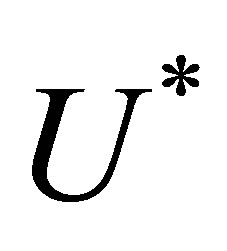 represents the searched solution. Thus, the resolution algorithm can be described as follows:
represents the searched solution. Thus, the resolution algorithm can be described as follows:
1) 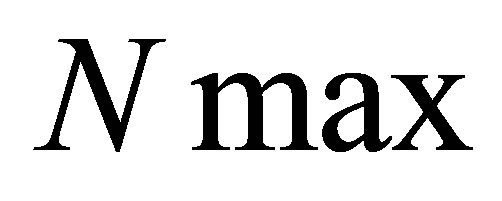 and
and  are fixed.
are fixed.
2)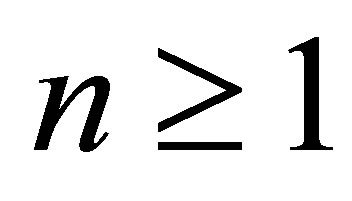 ,
, 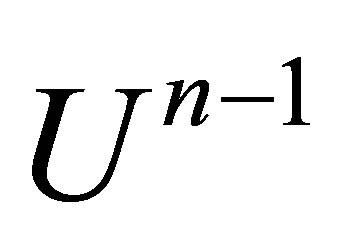 is known.
is known.
a)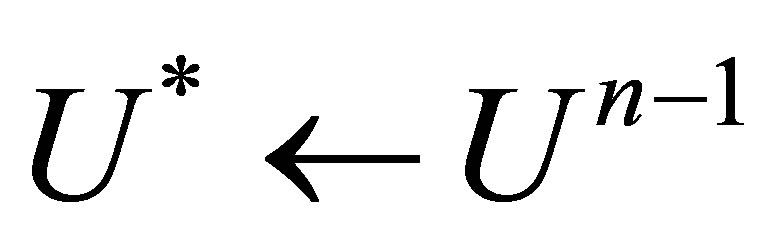 b) the beginning of the loop for linearization.
b) the beginning of the loop for linearization.
i) Solve
 (38)
(38)
ii) Update
 (39)
(39)
iii) If the condition on  or
or  is satisfied, the loop is stopped.
is satisfied, the loop is stopped.
c) .
.
In Appendix, we give the Freefem3d code we implement for solving the system.
5. Experimental Results on Real Data
We have validated our PDE model on real data of sand. The soil is sampled in the surface layer (0 - 20 cm) of an agricultural field at the INRA experimental site of Feucherolles (FEU) (50 km west of Paris) in France. The soil columns were scanned by means of a high resolution micro-CT machine (SIMCT Equipment: SIMBIOS, University of Abertay Dundee, Scotland) operating at 90 KeV and a current of 112 mA.
Using X-ray tomography we compute a 3D Computed Tomography (CT) image of a sand sample. The sizes of the original image are: 1650 μm × 1650 μm × 1745 μm. The voxel is cubic of resolution: 5 μm × 5 μm × 5 μm. Figure 2 shows slices (1650 μm × 1650 μm) of the 3D volume image. We extract from the (1650 μm × 1650 μm × 1745 μm) image a (400 μm × 400 μm × 400 μm) image for memory requirements and computing time reasons. Figure 3 shows successive slices (400 μm × 400 μm) of the (400 μm × 400 μm × 400 μm) 3D image extracted.
The second stage provides a set of voxels corresponding to pore space. The threshold is computed using the expected porosity of the sample. Figure 4 shows a cross section representing pore space (white color), the porosity is 35%. Using the geometric model for the 3D representation of the pore space described in [14,20-22], we calculate the network of balls.
Afterwards the balls are drained for the following values of water pressure ψ = −0.01 MPa and ψ = −0.001 Mpa corresponding respectively to situations that are relatively wet (high water pressure) and dry (low water pressure), respectively. For water pressure ψ = −0.01 MPa we get 649776 balls and for water pressure ψ = −0.001 Mpa we get 569175 balls. Figure 5 shows perspective views of the ball based pore space representation. Figure 6 shows the tetrahedral mesh building from all the centers of the balls.
We built the model for two different values of water pressures (high water pressure, wet and low water pressure, dry). Initial microbial biomass (40 g) is put on the mesh such that probability of microbial being in a node is proportional to the radius of the bal which corresponds to the node. At the beginning, 300 g fructose is uniformly distribute in the mesh. Diffusion coefficients of fructose, CO2 and DSM are equal to 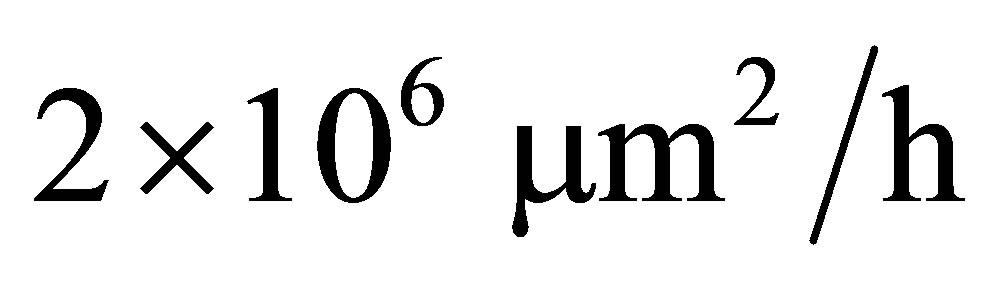 [26] while diffusion coefficient of microbe is equal to
[26] while diffusion coefficient of microbe is equal to 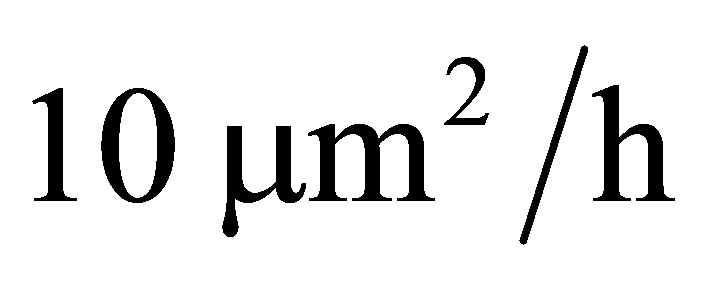 which is very small in comparison with diffusion coefficient of the others since we assume that microbial does not move. We compare experimental carbon flow curves as well as dissolved organic matter (DOC) amount with the ones provided by our PDE model. We test our PDE model for five different types of microbial species: Arthrobacter sp 3R, 7R and 9R, Rhodococcus sp 6L and 5L. Parameter values for simulation are taken from the investigation of Coucheney in [27] which are given in Table 1.
which is very small in comparison with diffusion coefficient of the others since we assume that microbial does not move. We compare experimental carbon flow curves as well as dissolved organic matter (DOC) amount with the ones provided by our PDE model. We test our PDE model for five different types of microbial species: Arthrobacter sp 3R, 7R and 9R, Rhodococcus sp 6L and 5L. Parameter values for simulation are taken from the investigation of Coucheney in [27] which are given in Table 1.
Figure 7 shows an example of the simulation results obtained from the PDE model. The four classical global evolution curves (CO2, DOC, microbial biomass and
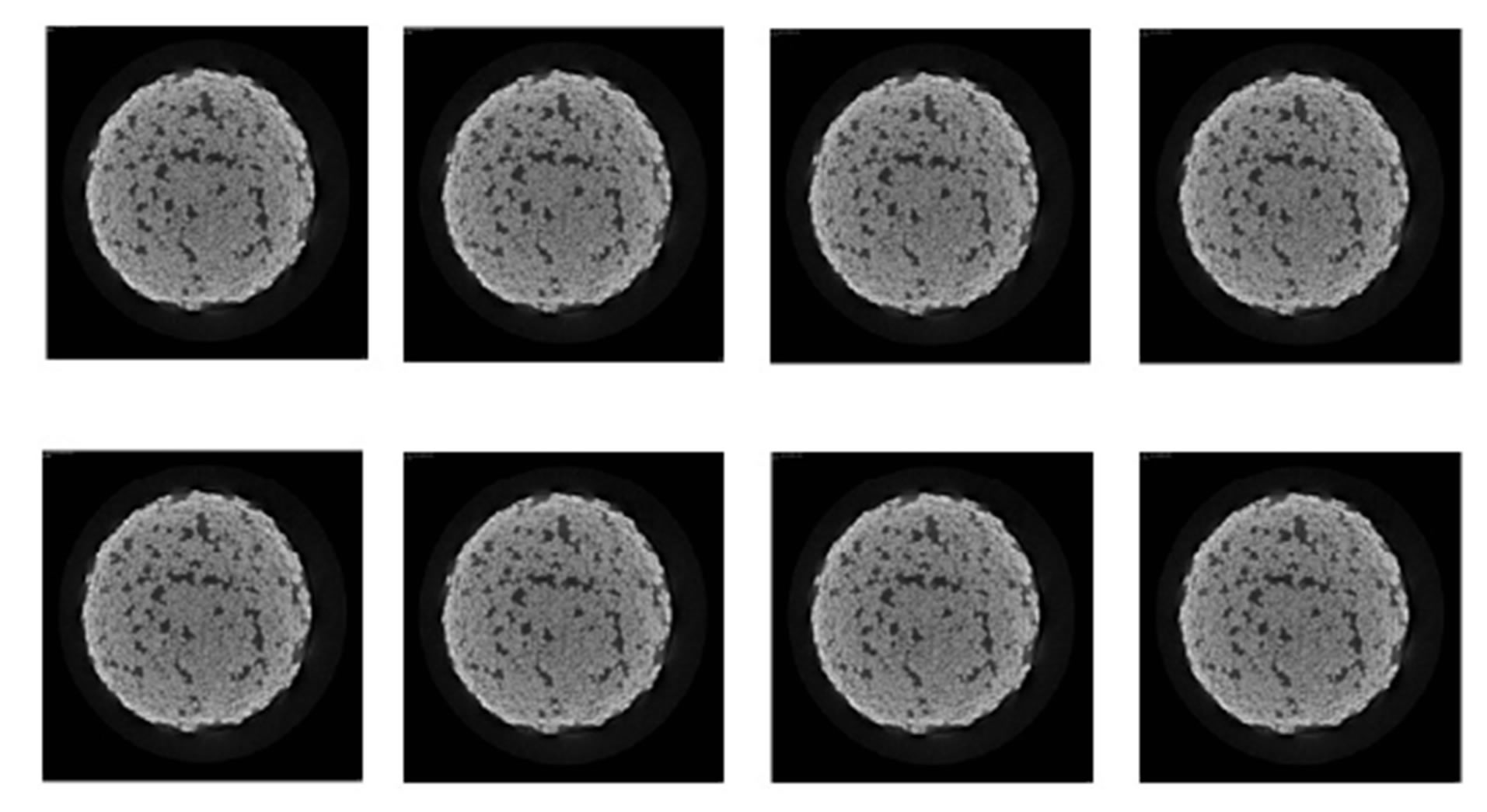
Figure 2. Successive slices (1650 μm × 1650 μm) of CT image of a sand soil sample.

Figure 3. Successive slices (400 μm × 400 μm) of the (400 μm × 400 μm × 400 μm) 3D image extracted.

Figure 4. Cross section representing pore space (white color), the porosity is 35%.
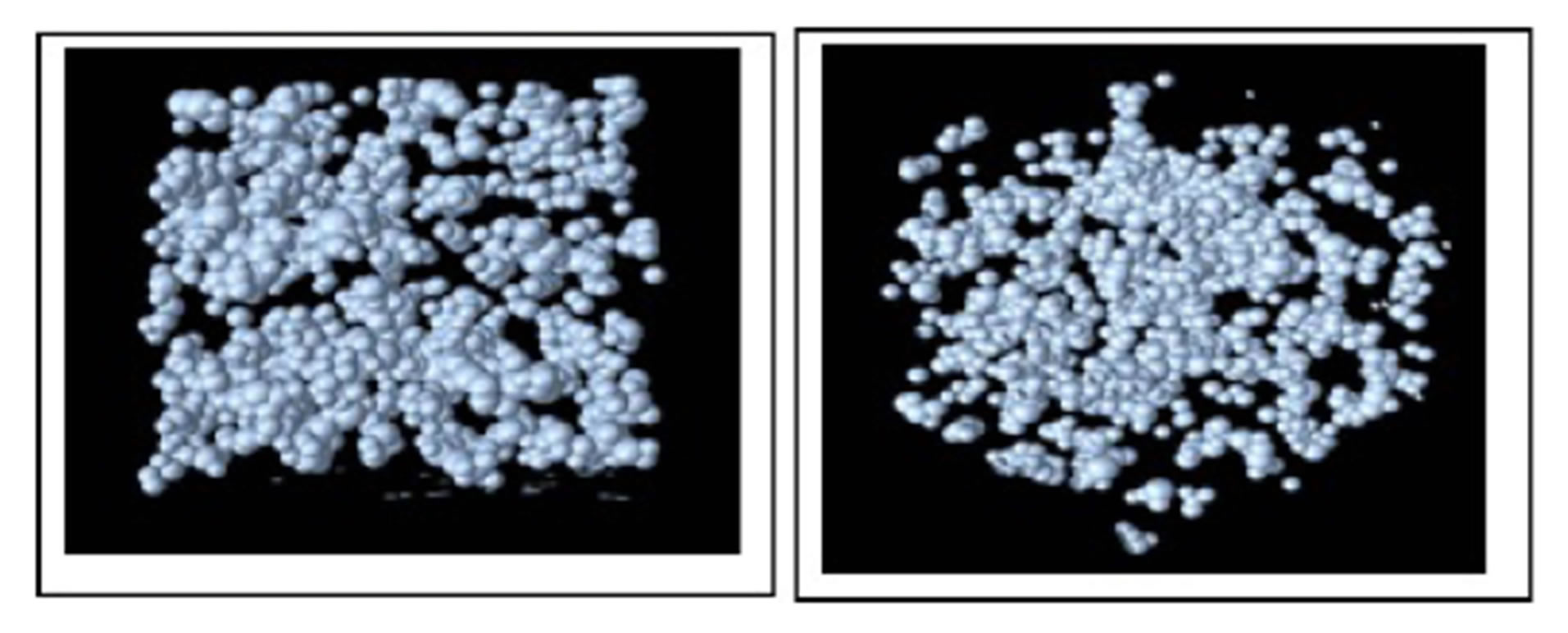
Figure 5. Perspective views of the ball based pore space representation. We display only the balls whose radius is at least 10.

Figure 6. A tetrahedral mesh building from the centers of 1000 balls.

Table 1. Parameter values are used in the simulation where ,
, 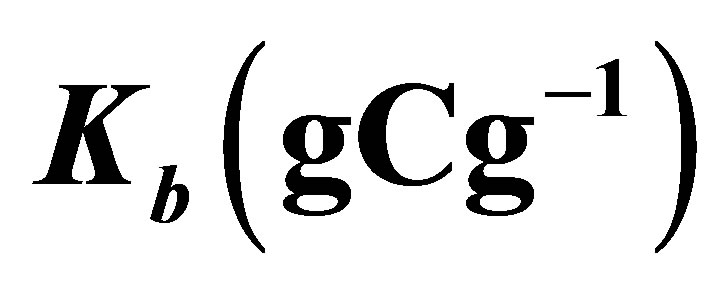 ,
,  and
and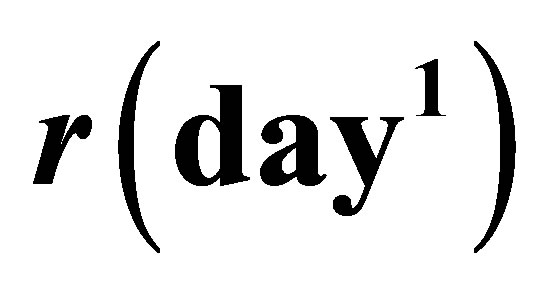 .
.
fructose) are presented for Rhodococcus sp 6L. One can see in the figure that fructose was rapidly decomposed by microbial for both cases (high and low water pressures). It was completely decomposed around the second day. The microbial biomass is therefore grows fast in the first two days. It is then decreases the days after. Since growth of CO2 is propotional to the microbial biomass in our model. Hence, the amount of CO2 grows fast at the second day then it grows slower the days after. This result is similar to what we observe from the data of CO2 for the both cases with high and slow water pressures.
In Figure 8, we show a comparison between experimental data and our PDE model about CO2 and DOC of of Arthrobacter sp 3R, 7R and 9R. The left hand side is about wet condition (high water pressure) and the right hand side is about dry condition (low water pressure). Black solid and black dash are about CO2 and DOC predicted from the PDE model. Grey solid with square marks and tri-angle marks are about CO2 and DOC from

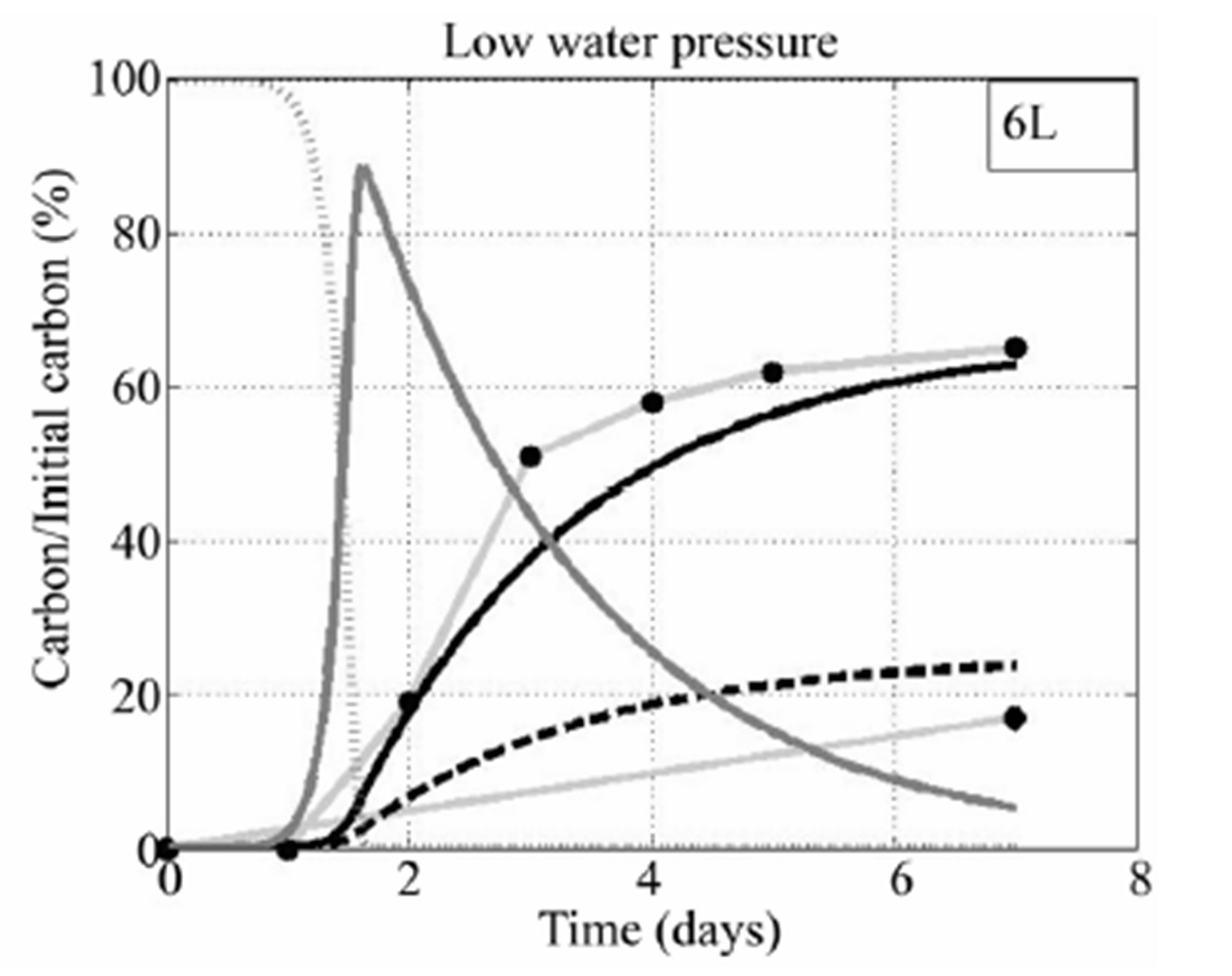
Figure 7. Simulation results of four biological elements of Rhodococcus sp 6L are presented. The above figure is about simulation with high water pressure and the below figure is about simulation with low water pressure. In the above figure: grey solid with square marks is about experimental CO2, grey solid with tri-angle marks is about experimental DOC. In the below figure: grey solid with circle marks is about experimental CO2, grey solid with tetra-angle marks is about experimental DOC. Both: black solid is about CO2 from the model, black dash is about DOC from the model, grey dark solid is about microbial biomass, grey dark dots is about fructose.
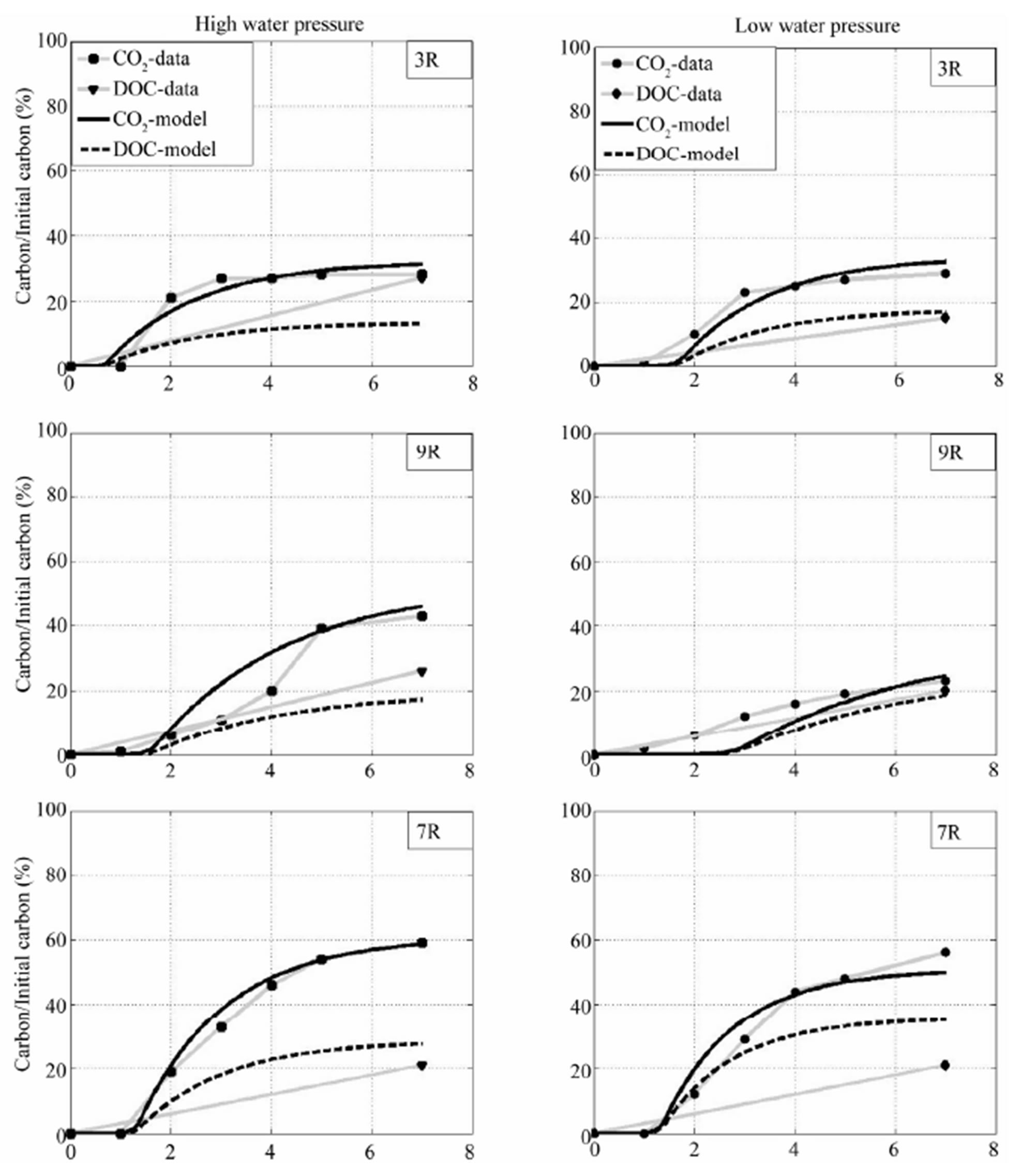
Figure 8. Comparison between model and experimental data for Arthrobacter sp 3R, 7R and 9R. On the left hand side is about high water pressure, on the right hand side is about low water pressure. Solid line is about CO2 from the PDE mode, dash line is about DOC from the model, square is about experimental CO2, circle is about experimental DOC.
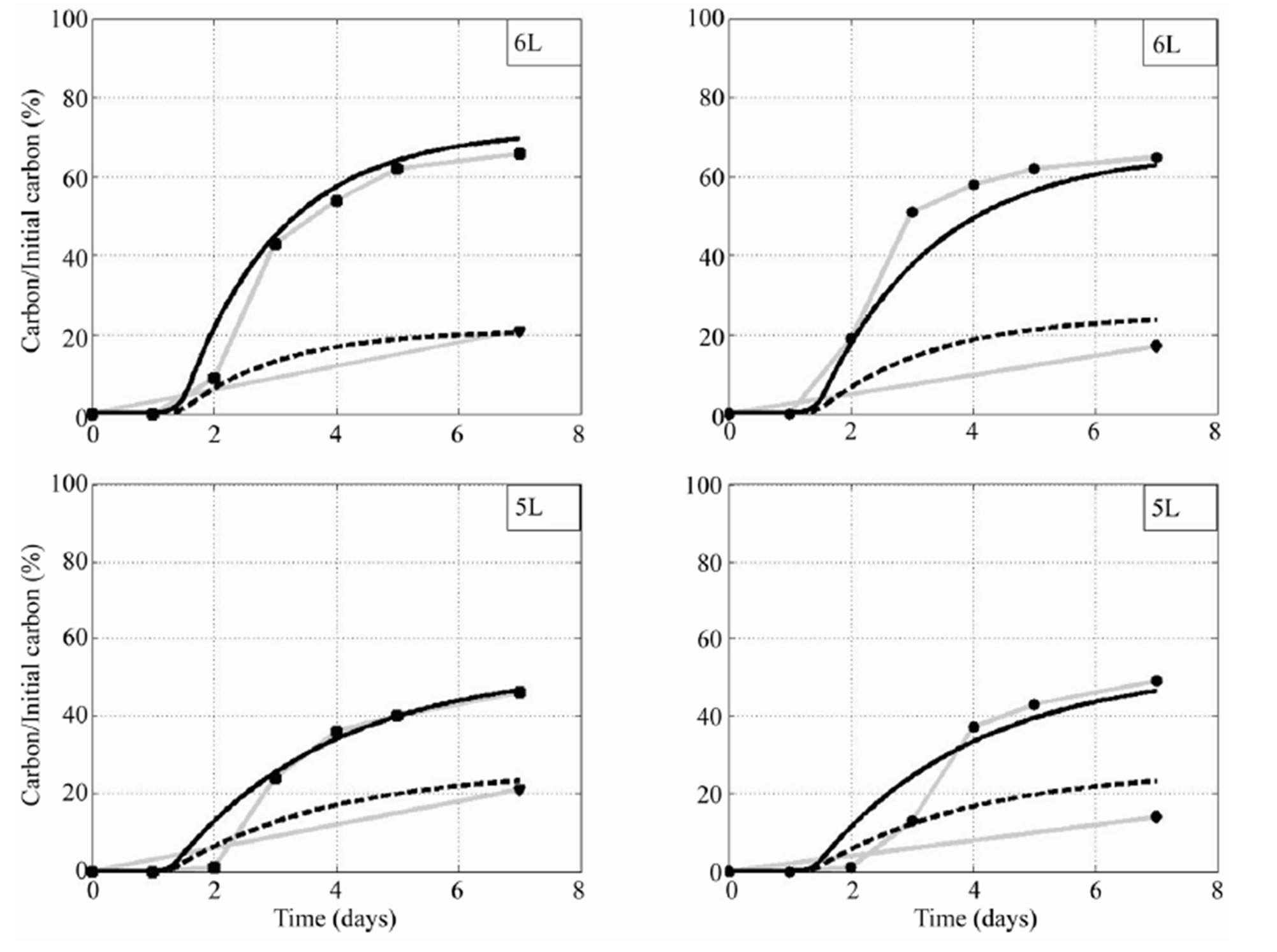
Figure 9. Comparison between model and experimental data forfor Rhodococcus sp 6L and 5L. On the left hand side is about high water pressure, on the right hand side is about low water pressure. Solid line is about CO2 from the PDE mode, dash line is about DOC from the model, square is about experimental CO2, circle is about experimental DOC.
experimental data in the wet condition (left), while grey solid with circle marks and tetra-angle marks are about CO2 and DOC from experimental data in dry condition (right). Similar comparison can be seen in Figure 9 for Rhodococcus sp 6L and 5L. It is noticed that we assumed that the sum of decomposable and undecomposable bacteria metabolites (DMM + UDMM) is simulated at the end of the experiment in order to measure the bound value of the DOC. Therefore, the DOC-model is expected greater than DOC-data. One can see in Figures 8 and 9 that DOC-model is greater than DOC-data in most cases except the case Arthrobacter 3R and 9R with high water pressure. It can be seen that CO2 fits very well to CO2-data for all cases. It is sligtly different between the two with Arthrobacter 7R in low water pressure.
6. Conclusion and Perspectives
In this study we have proposed a new model of organic matter decomposition in the 3D soil pores. The novelties of our approach are to consider the real 3D microstructures of soil, to take into account diffusion and transformation processes. To our knowledge, this is the first attempt to describe diffusion process in 3D soil structure thanks to the strength of PDEs. We applied our PDE model to real CT images of soil in which we add realistic amount of organic matter and microorganisms. We validated our model to experimental results. In particular, we compare experimental carbon flow curves as well as DOC amount with the ones provided by our PDE model at two different water pressures. The simulation results show that our PDE model fits reasonably well to the experimental results. In this current contribution, we just consider the dynamics of single microbial species. In future studies, simulations with real experimental data will be carried out with our model in order to analyze microbial competition of degradation under different water contents.
7. Acknowledgements
The authors thank Valrie POT for the acquisition of CT images and for many fruitful discussions. We are grateful to Olivier Pironneau, Frdric Hecht, Stphane Del Pino for their explainations and adds to adapt the freefem3d software to the model implementation. We also acknowledge with thanks to Mamadou Sy and Abdou Sne according to mathematical and numerical useful comments and help.
REFERENCES
- C. Fang, P. Smith, J. U. Smith and J. B. Monrieff, “Incorporating Microorganisms as Decomposers into Models to Simulate Soil Organic Matter Decomposition,” Geoderma, Vol. 129, No. 3-4, 2005, pp. 139-146. http://dx.doi.org/10.1016/j.geoderma.2004.12.038
- J. P. Schimel and M. N. Weintraub, “The Implications of Exoenzyme Activity on Microbial Carbon and Nitrogen Limitation in Soil: A Theoretical Model,” Soil Biology and Biochemistry, Vol. 35, No. 4, 2002, pp. 549-563. http://dx.doi.org/10.1016/S0038-0717(03)00015-4
- Manzoni and Porporato, “Soil Carbon and Nitrogen Mineralization: Theory and Models across Scales,” Soil and Biochemistry, Vol. 41, No. 7, 2009, pp. 1355-1379.
- T. Long and D. Or, “Aquatic Habitats and Diffusion Constraints Affecting Microbial Coexistence in Unsatured Porous Media,” Water Resources Research, Vol. 41, No. 8, 2005, 10 p. http://dx.doi.org/10.1029/2004WR003796
- I. Joachim, P. Christian, S. Thilo and K. Ellen, “MicroScale Modeling of Carbon Turnover Driven by Microbial Succession at a Biogeochemical Interface,” Soil Biology and Biochemistry, Vol. 40, No. 4, 2008, pp. 864-878. http://dx.doi.org/10.1016/j.soilbio.2007.10.018
- S. D. Allison, “Cheaters, Diffusion and Nutrients Constrain Decomposition by Microbial Enzymes in Spatially Structured Environments,” Ecology Letters, Vol. 8, No. 6, 2005, pp. 626-635. http://dx.doi.org/10.1111/j.1461-0248.2005.00756.x
- Y. A. Vetter, J. W. Deming, P. A. Jumars and B. B. Krieger-Brockett, “A Predictive Model of Bacterial Foraging by Means of Freely Released Extracellular Enzymes,” Microbial Ecology, Vol. 36, No. 1, 1998, pp. 75-92. http://dx.doi.org/10.1007/s002489900095
- C. J. Moran and A. B. McBratney, “Acquisition and Analysis of Three Component Digital Images of Soil Structure,” Journal of Soil Science, Vol. 43, No. 3, 1992, pp. 541-549. http://dx.doi.org/10.1111/j.1365-2389.1992.tb00159.x
- J. Bouma, P. A. Droogers and G. Boer, “Parameters for Describing Soil Macroporisity Derived from Staining Patterns,” Geoderma, Vol. 83, No. 3-4, 1998, pp. 293-308. http://dx.doi.org/10.1016/S0016-7061(98)00005-6
- A. Ringrose-Voase, “Measurement of Soil Macropore Geometry by Image Analysis of Sections through Impregnated Soil,” Plant and Soil, Vol. 183, No. 1, 1996, pp. 27-47. http://dx.doi.org/10.1007/BF02185563
- Y. Capowiez, “Difference in Borrowing Behaviour 661 and Spatial Interaction between the Two Earthworm Species Aporrectodea nocturna and Allobophora chlorotica,” Biology and Fertility of Soils, Vol. 30, No. 4, 2000, pp. 341-346. http://dx.doi.org/10.1007/s003740050013
- O. Monga, N. F. Ngom and J. F. Delerue, “Representing Geometric Structures in 3D Tomography Soil Images: Application to Pore Space Modeling,” Computers and Geosciences, Vol. 33, No. 9, 2007, pp. 1140-1161. http://dx.doi.org/10.1016/j.cageo.2006.11.015
- S. Peth, R. Horn, F. Beckmann, T. Donath, J. Fischer and A. J. M. Smucker, “Three Dimensional Quantification of Intra Aggregate Pore Space Features Using Synchrotron Radiation Based Microtomography,” Soil Science Society of America Journal, Vol. 72, No. 4, 2008, pp. 897-907. http://dx.doi.org/10.2136/sssaj2007.0130
- O. Monga, M. Bousso, P. Garnier and V. Pot, “3d Geometrical Structures and Biological Activity: Application to Microbial Soil Organic Matter Decomposition in Pore Space,” Ecological Modelling, Vol. 216, No. 3-4, 2008, pp. 291-302. http://dx.doi.org/10.1016/j.ecolmodel.2008.04.015
- A. M. Tartakovsky, T. D. Scheibe and P. Meakin, “PoreScale Model for Reactive Transport and Biomass Growth,” Journal of Porous Media, Vol. 12, No. 5, 2009, pp. 417-434. http://dx.doi.org/10.1615/JPorMedia.v12.i5.30
- R. E. Falconer, J. L. Bown, N. A. White and J. W. Crawford, “Biomass Recycling: A Key to Effcient Foraging by Fungal Colonies,” OIKOS, Vol. 116, No. 9, 2007, pp. 1558-1568. http://dx.doi.org/10.1111/j.0030-1299.2007.15885.x
- N. Marilleau, C. Cambier, A. Drogoul, J. L. Chotte, E. Perrier and E. Blanchart, “Multiscale MAS Modelling to Simulate the Soil Environment: Application to Soil Ecology,” Simulation Modelling Practice and Theory, Vol. 16, No. 7, 2008, pp. 736-745. http://dx.doi.org/10.1016/j.simpat.2008.04.021
- S. Del Pino and O. Pironneau, “Asymptotic Analysis and Layer Decomposition for the Couplex Exercise,” Computational Geosciences, Vol. 8, No. 2, 2007, pp. 149-162. http://dx.doi.org/10.1023/B:COMG.0000035076.46993.dd
- C. Dobrzynski, P. J. Frey, B. Mohamadi and O. Pironneau, “Fast and Accurate Simulations of Air-Cooled Structures,” Computer Methods applied in Mechanical Engineering, Vol. 195, 2006, pp. 3168-3180.
- N. F. Ngom, P. Garnier, O. Monga and S. Peth, “Extraction of Three Dimensional Soil Pore Space from Microtomography Images Using a Geometrical Approach,” Geoderma, Vol. 163, No. 1-2, 2011, pp. 127-134. http://dx.doi.org/10.1016/j.geoderma.2011.04.013
- N. F. Ngom, O. Monga, M. M. O. Mohamed and P. Garnier, “3D Shape Extraction Segmentation and Representation of Soil Microstructures Using Generalized Cylinders,” Computers and Geosciences, Vol. 39, 2012, pp. 50-63. http://dx.doi.org/10.1016/j.cageo.2011.06.010
- O. Monga, M. Bousso, P. Garnier and V. Pot, “Using Pore Space 3d Geometrical Modelling to Simulate Biological Activity: Impact of Soil Structure,” Computers and Geosciences, Vol. 35, No. 9, 2009, pp. 1789-1801. http://dx.doi.org/10.1016/j.cageo.2009.02.007
- J. D. Murray, “Mathematical Biology. I: An Introduction,” Springer, 2003, 551 p.
- P. J. Frey, H. Borouchaki and P. L. George, “3D Delaunay Mesh Generation Coupled with an Advancing-Front Approach,” Computer Methods in Applied Mechanics and Engineering, Vol. 157, No. 1-2, 1998, pp. 115-131. http://dx.doi.org/10.1016/S0045-7825(97)00222-3
- P. L. George and H. Borouchaki, “Premières Expériences de Maillage Automatique par une Mthode de Delaunay Anisotrope en Trois Dimensions,” INRIA, 2002, 272 p.
- R. C. Weast, “Handbook of Chemistry and Physics 62nd Edition 1981-1982,” CRC Press, Inc., 1981, 1700 p.
- E. Coucheney, “Effets Combinés de Facteurs Climatiques et de la Diversité sur le Fonctionnement de Communautés Bactériennes: Respiration et Métabolomique,” Université Pierre et Marie Curie, 2009, 194 p.
Appendix. Algorithm Code Using Freefem3D
The freefem3d code corresponding to the algorithm is the following:
Step 1. Getting the mesh from the source file.
meshM = read(medit, “tetranuage.mesh”)
Step 2. Defining the data. Functions  of type femfunction defined on the mesh
of type femfunction defined on the mesh  are used to represent reaction terms of the system. To solve the nonlinearity of the reaction functions, we use the same type to define approximate functions eb, ef, em1, em2, en, and ec. The same function type is used to build terms of correction db, df, dm1, dm2, dn, and dc. The parameters such as diffusion coefficients, growth and death rate of MB are declared using double type.
are used to represent reaction terms of the system. To solve the nonlinearity of the reaction functions, we use the same type to define approximate functions eb, ef, em1, em2, en, and ec. The same function type is used to build terms of correction db, df, dm1, dm2, dn, and dc. The parameters such as diffusion coefficients, growth and death rate of MB are declared using double type.
Step 3. Defining and initializing the functions representing variable densities. Initial functions are declared with the femfunction type defined on M. The ofstream function permits to create a file to save solutions. The quantities of the variables are obtained by integrating their density in the pore space represented by the mesh M. Thus, we use the following Freefem3d code to implement the numerical scheme:
// opening of a file named “outputpathname” to save results of stream out put = of stream(“outputpathname”);
// saving of the time and initial quantities
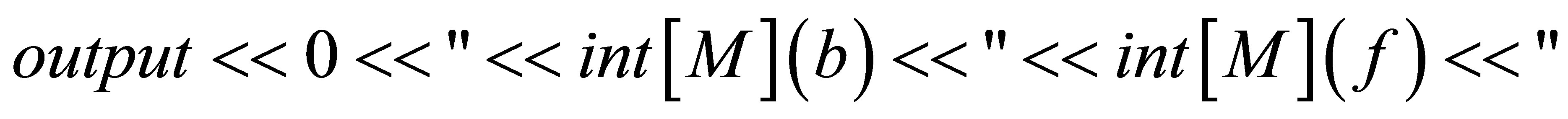
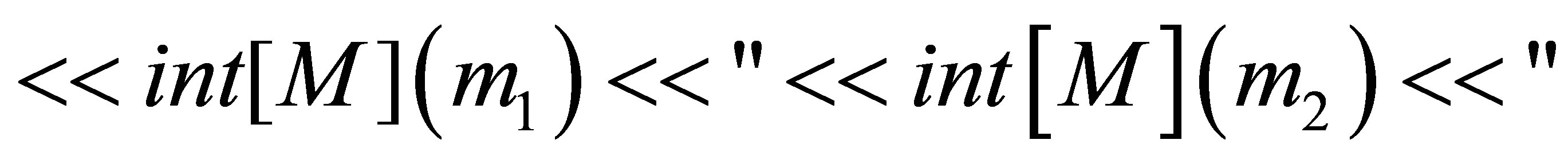
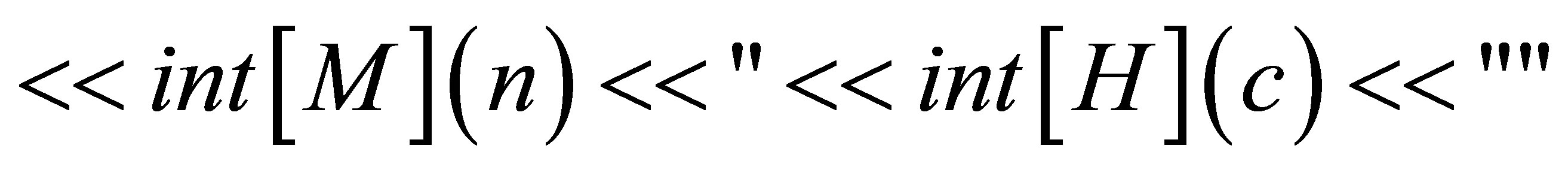
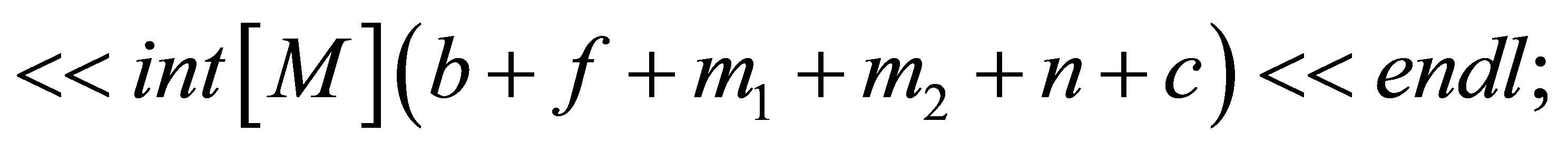
// defining the time loop, 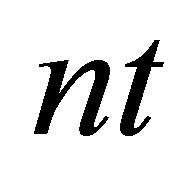 is the number of time steps
is the number of time steps

{
// we initialize the iteration counter to solve the nonlinearity
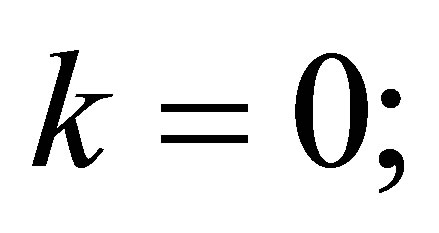
// we initialize approximate functions
 ;
;
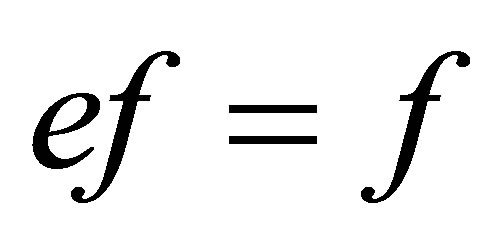 ;
;
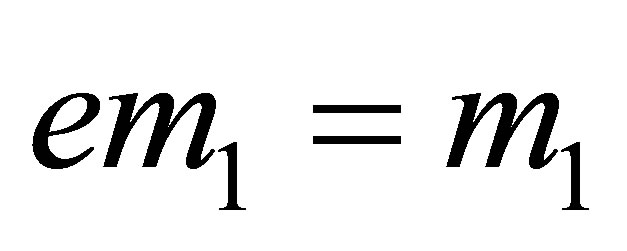 ;
;
 ;
;
 ;
;
 ;
;
// loop for linearizing the system do
{
//we redefine the reaction terms as functions of approximate terms.
// solving the system to find correction terms.
// Db, Df, Dn, Dc are diffusion coefficients.
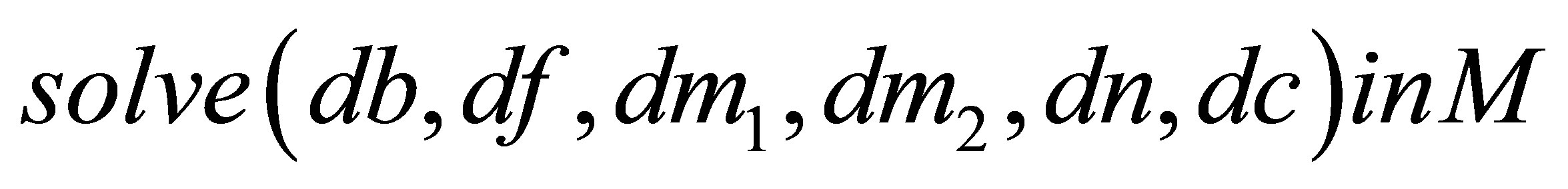
{
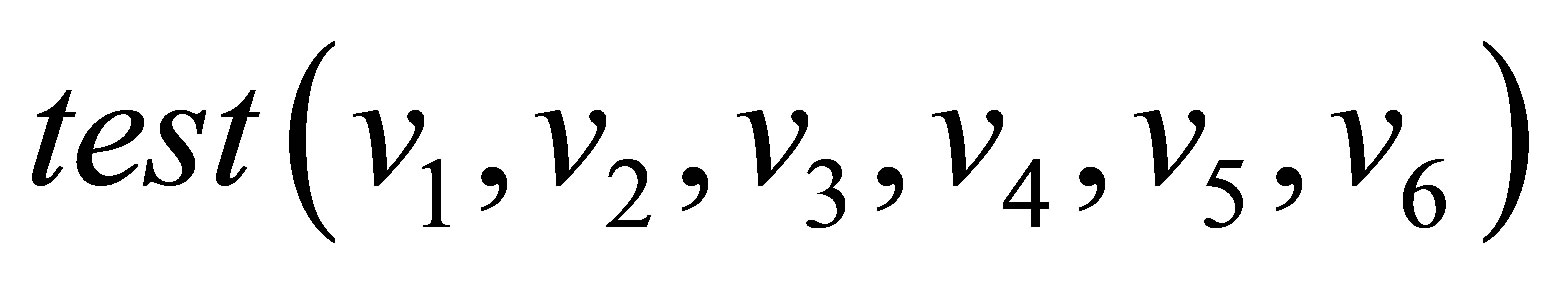
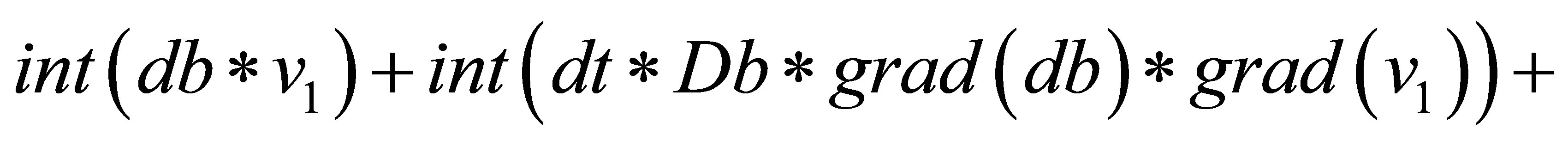

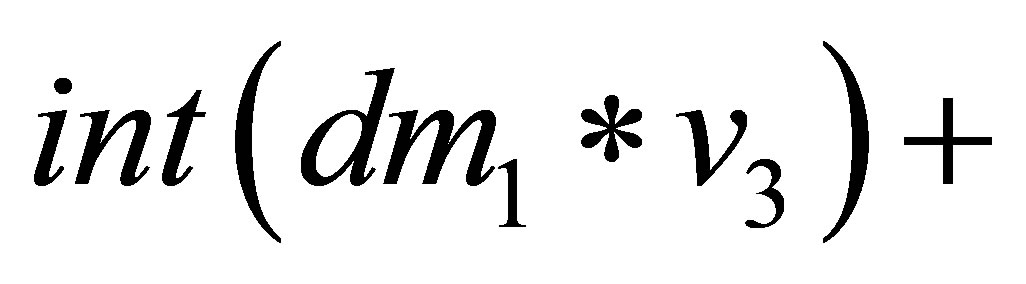

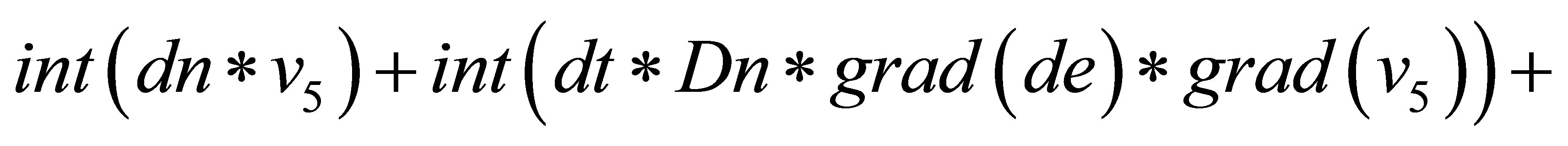

=
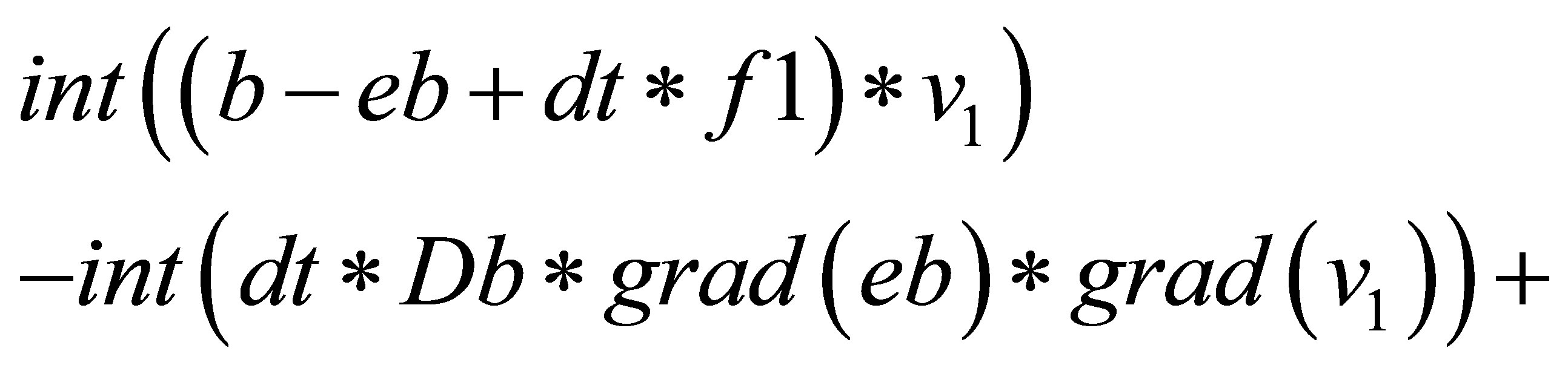
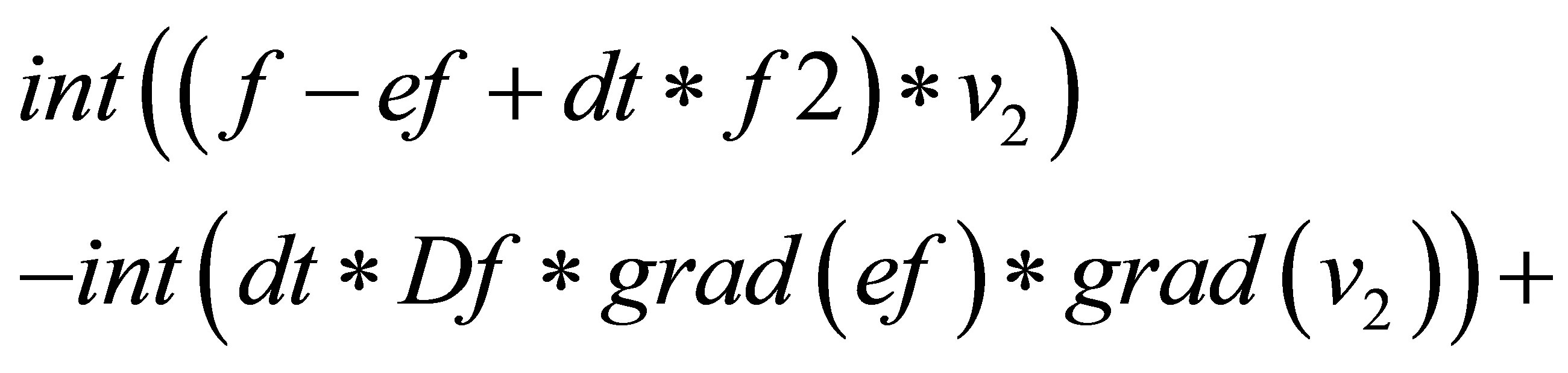
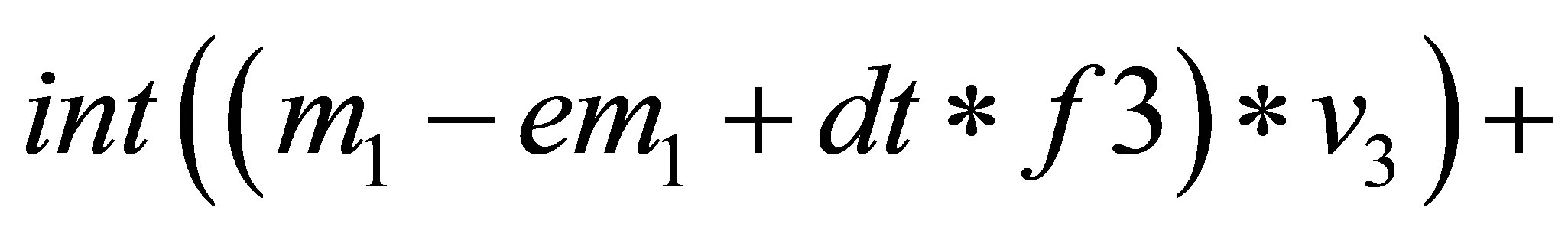
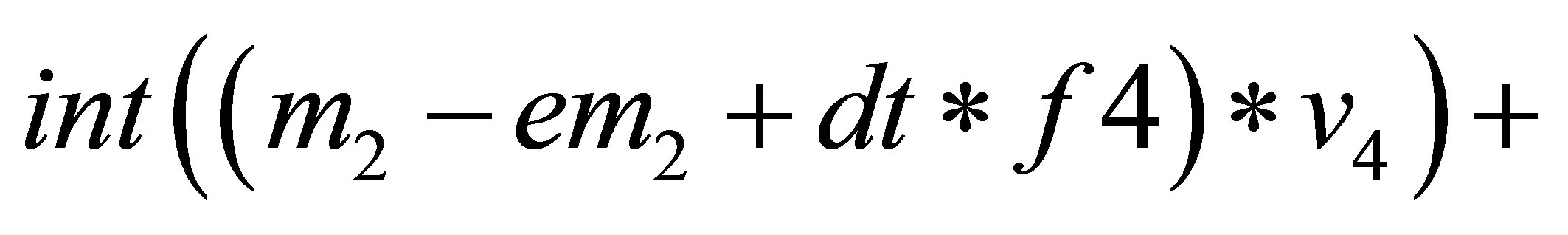

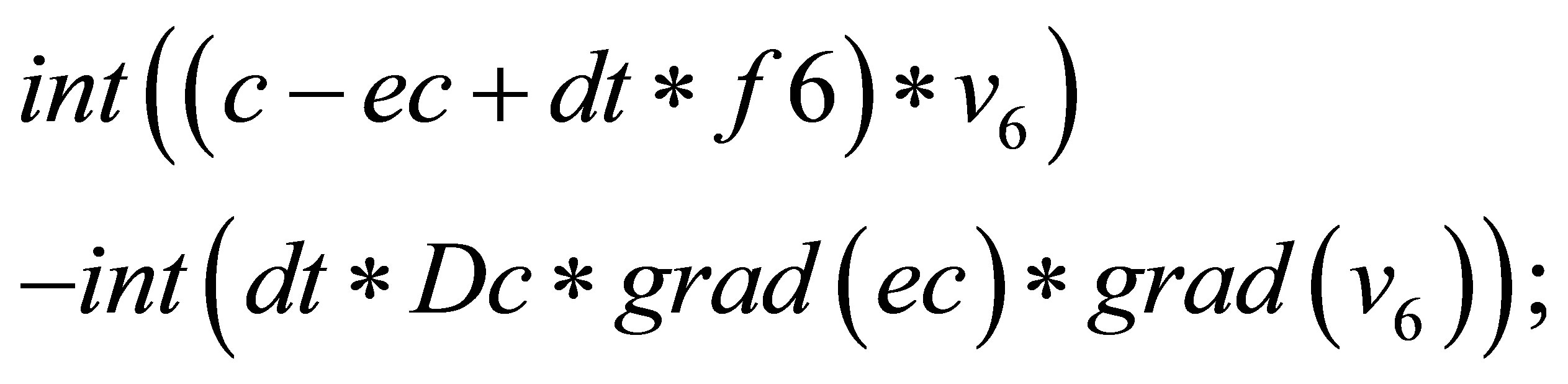
}
// updating of approximate functions
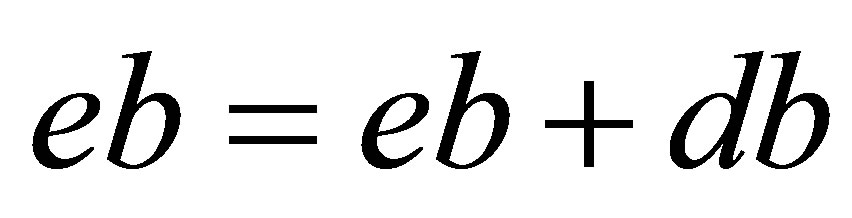 ;
;
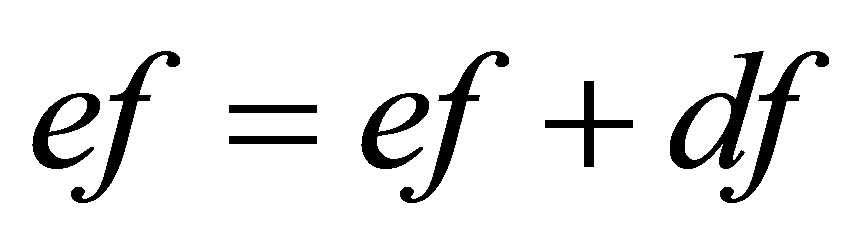 ;
;
 ;
;
 ;
;
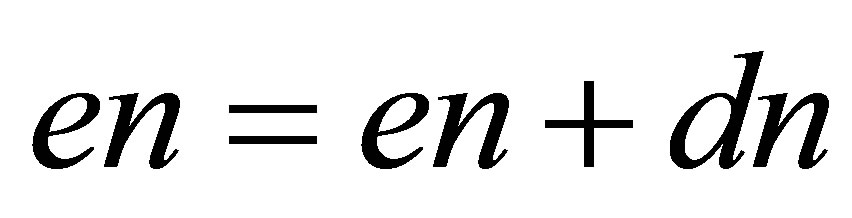 ;
;
 ;
;
// incrementing of the counter 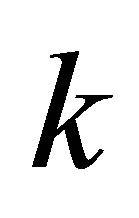
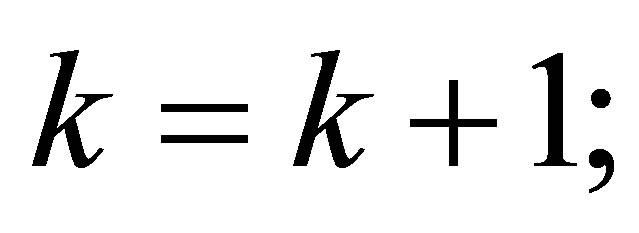
// we stop the loop if one of the criteria is satisfied.
}
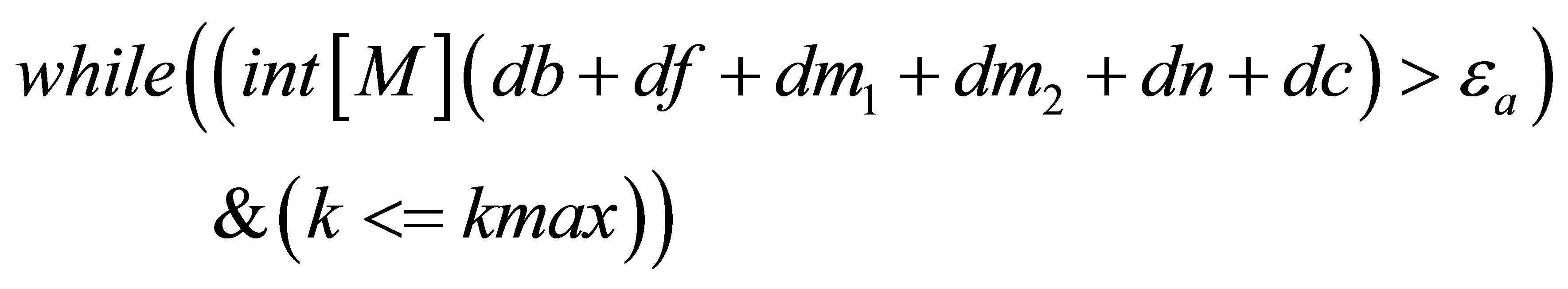
// updating the solutions
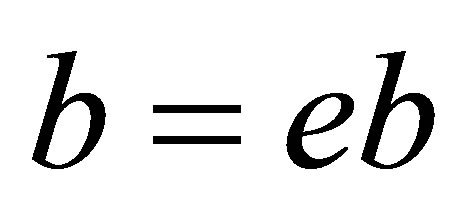 ;
;
 ;
;
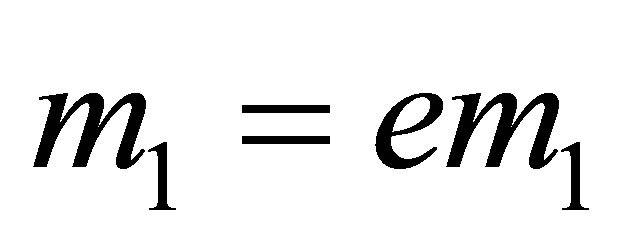 ;
;
 ;
;
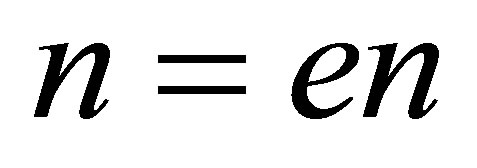 ;
;
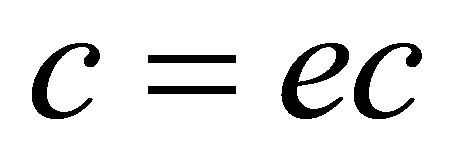 ;
;
// updating time counter

// We save solutions.
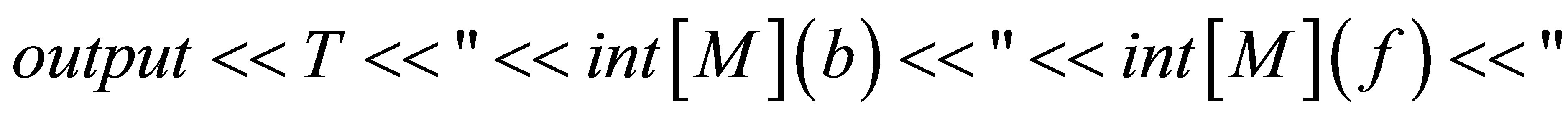

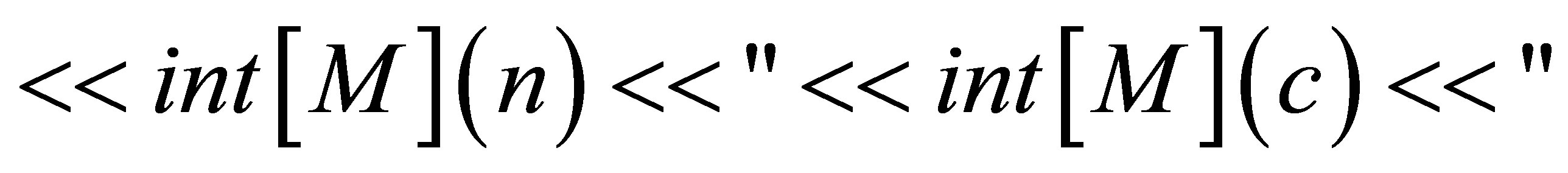
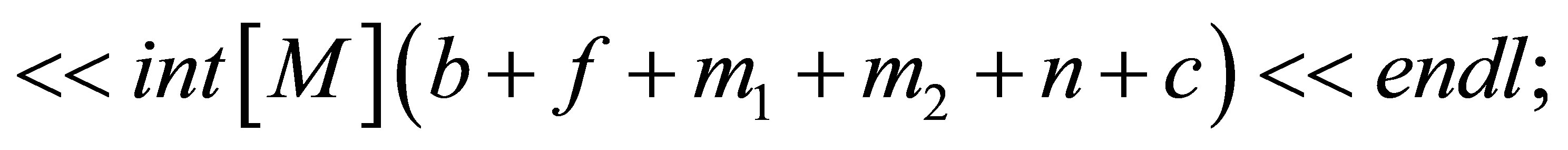
// We save the isovalues.
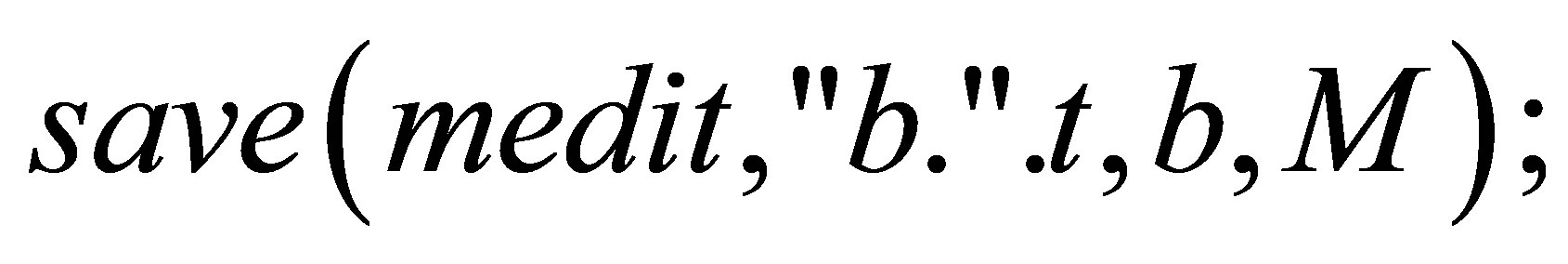



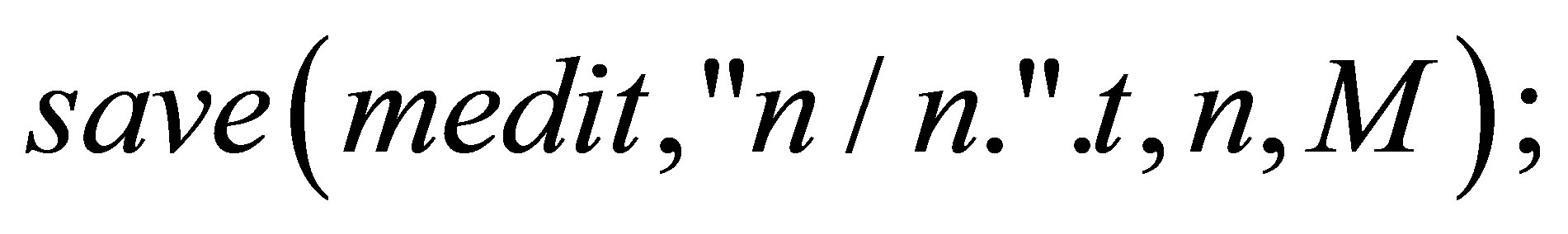
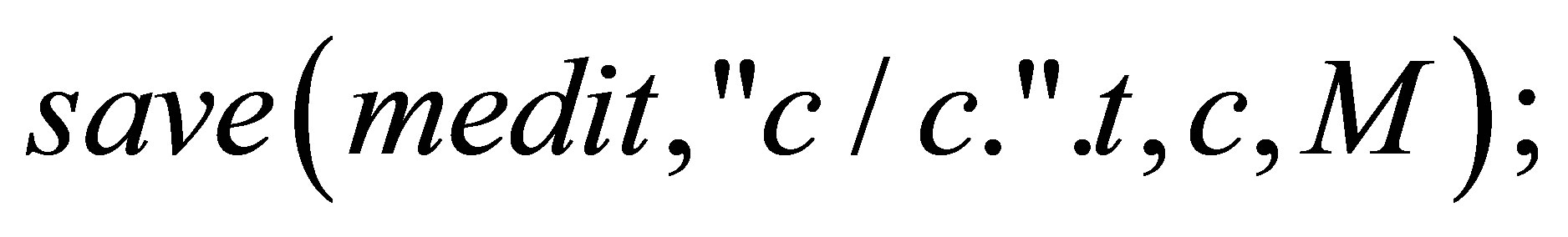
}
//End of progam
NOTES
*Corresponding author.

