International Journal of Geosciences
Vol.4 No.10(2013), Article ID:41165,6 pages DOI:10.4236/ijg.2013.410129
Crustal Thickness of Funafuti Using Receiver Function Analysis
Department of Applied Geophysics, Indian School of Mines, Dhanbad, India
Email: vardhan.sri@gmail.com
Copyright © 2013 V. Srivardhan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property V. Srivardhan. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received August 16, 2013; revised September 15, 2013; accepted October 11, 2013
Keywords: Receiver Function Analysis; Funafuti; Mohorovičić Discontinuity; Deconvolution of Three Component Seismogram; Iterative Time Domain Deconvolution
ABSTRACT
In this study, the characterization of the depth of the Mohorovičić discontinuity under the crust of Funafuti island was determined by analyzing the 3 component seismograms from 54 different earthquake events recorded by the station between 2008 and 2012. These seismograms were from teleseismic earthquakes whose epicenter lay at distances greater than 3000 km from the station. The seismograms were iteratively deconvolved in the time domain to remove the unwanted noise and then stacked to obtain better receiver functions. For analysis of the receiver functions, it was assumed that the range in which the Vp/Vs ratio would lie for the given region would be between 1.60 - 1.85 and the depth of the discontinuity was assumed to lie between 5 - 20 km. Analysis of the receiver functions showed that the Mohorovičić discontinuity was at a depth of 11 km and the Vp/Vs ratio was 1.75 for the region.
1. Introduction
Funafuti is an atoll which is the capital of the island nation Tuvalu. The Tuvalu islands are a group of nine islands, which are located midway between Australia and Hawaii. Historically the nation is believed to be first inhabited by migrated Polynesians. These separate islands were together earlier known as Ellice Islands and were ruled by the British Empire. In 1974 the people of Tuvalu voted for the creation of a separate nation and on 1st October 1978 their dreams were realized and Tuvalu became fully independent within the Commonwealth. Funafuti was also historically the first site where drilling expeditions were first done and borings down to 400 m were dug by the Royal Society of London to study the coral rocks and reefs.
Receiver function analysis is a very easy and an economical method [1] used to map the subsurface structures. It becomes very expensive if conventional seismic imaging techniques using explosives and geophones are used or if other techniques like wireline logging and downhole logging are used. Receiver function analysis has been used many times in the past [2,3] to find out the depth of the Mohorovičić discontinuity which is the boundary between the lower crust and the upper mantle.
2. Receiver Function Analysis
2.1. Propagation of Seismic Waves through the Earth
The Earth is stratified into many horizontal layers. Each layer has its characteristic physical and chemical properties. A simple structural model of the Earth is shown in Figure 1.
The Mohorovičić discontinuity (Moho) is defined as the depth at which the velocity of the P waves exceeds 7.6 km/s [4]. There is also a sudden increase in the S wave velocity. Typically in continental crust this discontinuity is found at depths between 30 km and 60 km and in oceanic crust it is found between 5 km and 9 km. This sudden change in the P and S wave velocity is attributed to the sudden change in the mineralogical properties [5] of the crustal medium. This sudden change affects the density and elastic properties of the crustal medium which typically control the velocity of the seismic waves.
Receiver functions are composed of teleseismic waves
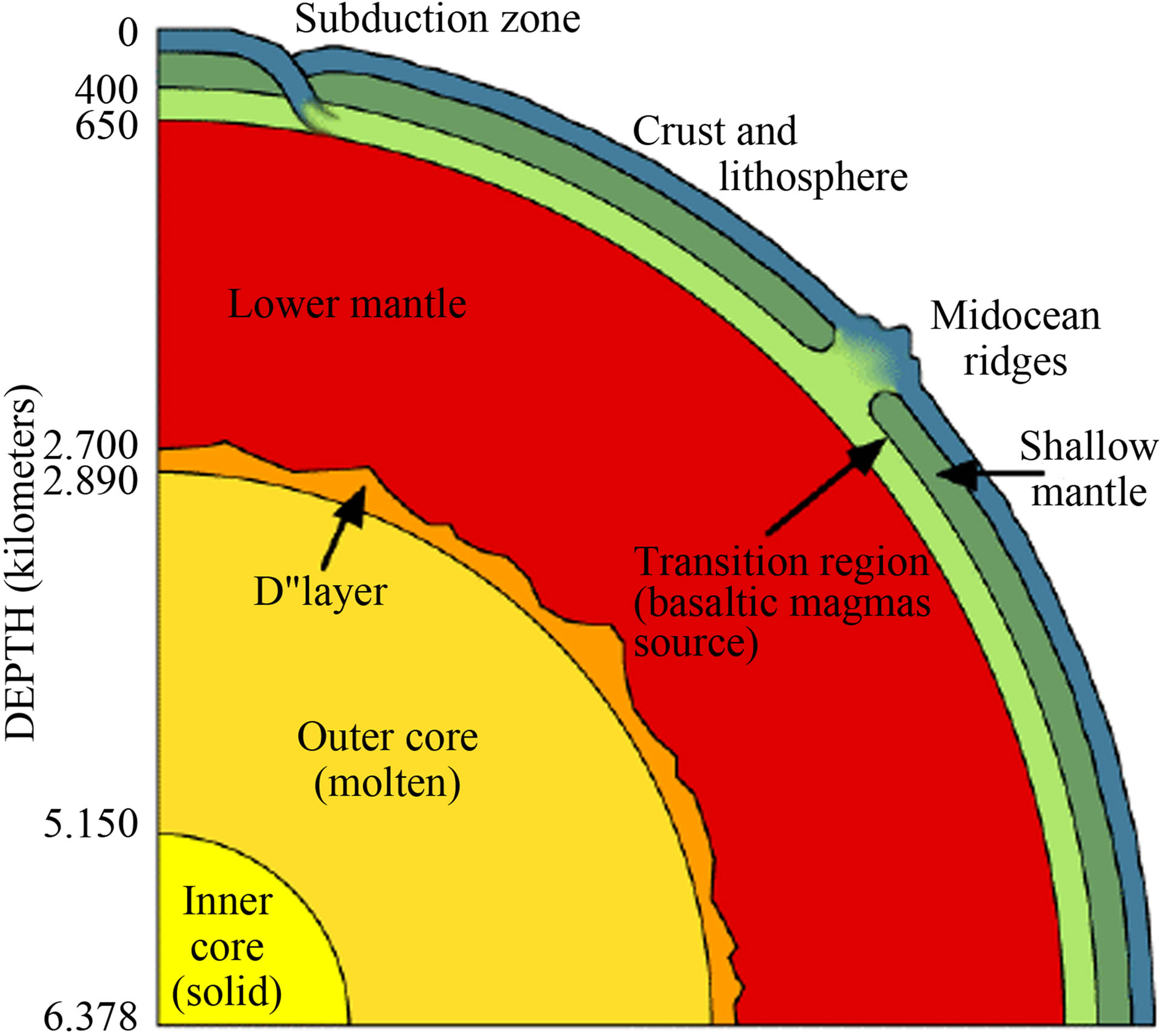
Figure 1. A simplified illustration of the internal structural of the Earth. Taken from [1].
which arrive at a receiver station from very large distance earthquakes. The distances are taken large as the waves can then be approximated to plane wavefronts and the waves then reach the station almost vertically after passing through the Moho [6]. At the Moho the P wave splits into the Pp and Ps phases which are recorded by the seismogram. Since the rays are approximated to be near vertical, a simple time difference in arrival times between the phases corresponds to the depth of the discontinuity provided the velocity model is known. The resulting seismogram is a three component seismogram with two horizontal and one vertical components. Theoretically one of the horizontal components must not record any signal, but this does not happen in reality as the Earth is not completely homogenous in structure. The resulting seismograms contain noise in the form source effects, propagation path effects, near receiver function effects and due to the instrument response. There will also be reverberations which will be recorded. The near source effects modify the seismic waves near the source of the signal by creating reverberations and internal reflections due to the geological conditions of the source and they effect the transmission of the teleseismic waves and makes its nature very complex. The propagation path effects are due to the various heterogeneities that the wave encounters when propagating through the Earth which causes it lose energy. The near receiver effects are due to the local geological conditions near the receiver which dominates when the seismic waves approach it. The resultant seismograms are due to the combination of all the above effects as shown Equation (1). UV(t), UR(t), UT(t) are the vertical, radial, and the transverse components of the seismogram. The operator * is a convolution operator and t is the time variable. I(t), P(t),
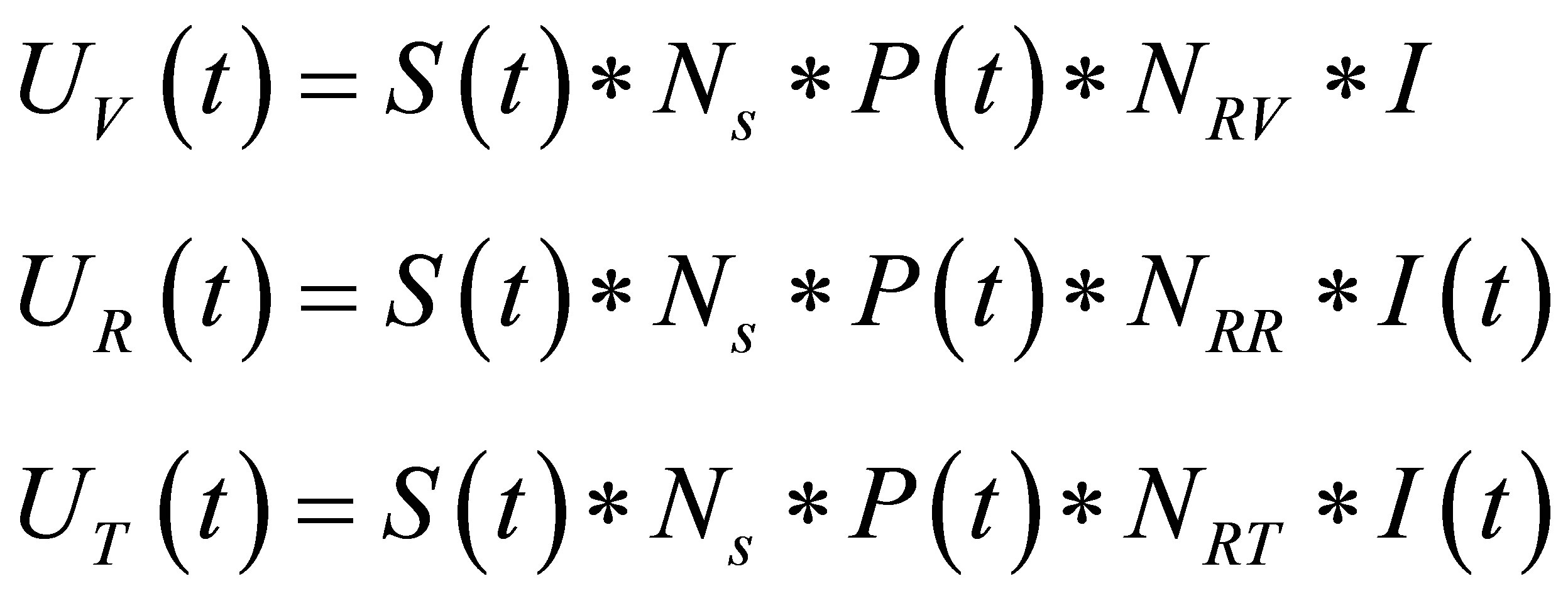 (1)
(1)
Ns, and {NRV, NRR, NRT} are the instrument response effect, path effect, source effect and the corresponding receiver function effects. S(t) is the Earths response function. The resultant seismogram is taken as a convolution of all the effects. To remove all these effects and obtain the Earth’s response function at the receiver which is otherwise called as receiver function, a deconvolution operation must be performed. Figure 2 shows a simple illustration of how a receiver function is created after an iterative time domain deconvolution.
Earthquake events used for receiver function analysis of the crustal structure beneath a station must meet several requirements. To ensure that the Pp and Ps wavefields are naturally separated on the vertical and horizontal components of the seismogram, only nearly vertical emergent angled seismic waves must be selected. This is achieved by selecting only those earthquake events which are teleseismic in origin with epicentral distances varying between 30˚ and 90˚ from the receiver. The above approximations are valid when the assumption is made that the travel paths of the up going events progressively becomes vertical as it arrives at the receiver. Further only those earthquakes are chosen whose magnitudes are equal to or greater than 6.0 to ensure a good signal to noise ratio. In addition the seismograms are visually verified to ensure that the P arrivals are impulsive and only then are they sent for further processing.
2.2. Deconvolution
Several deconvolution techniques like water-level deconvolution technique [7], iterative time-domain deconvolution technique [8] and the multi spectral correlation techniques have been proposed [9] to calculate the receiver functions. When the signal to noise ratio is high and the signal is wideband, all of the above mentioned techniques are equally good. Thus the best approach to compute receiver functions is to compute it for events of large magnitude. However, for studies which need a good back azimuthal coverage there are never enough observations from all azimuths, and consequently one is forced to incorporate signals from smaller events which leads to instability in the deconvolution operation done by spectral division. Iterative time domain deconvolution technique has been found to work very well even in the presence of noisy data and is also used in receiver function analysis in this study. The principle utilized in the time domain deconvolution technique is that receiver functions when convolved with the vertical component of the seismogram would produce the horizontal component
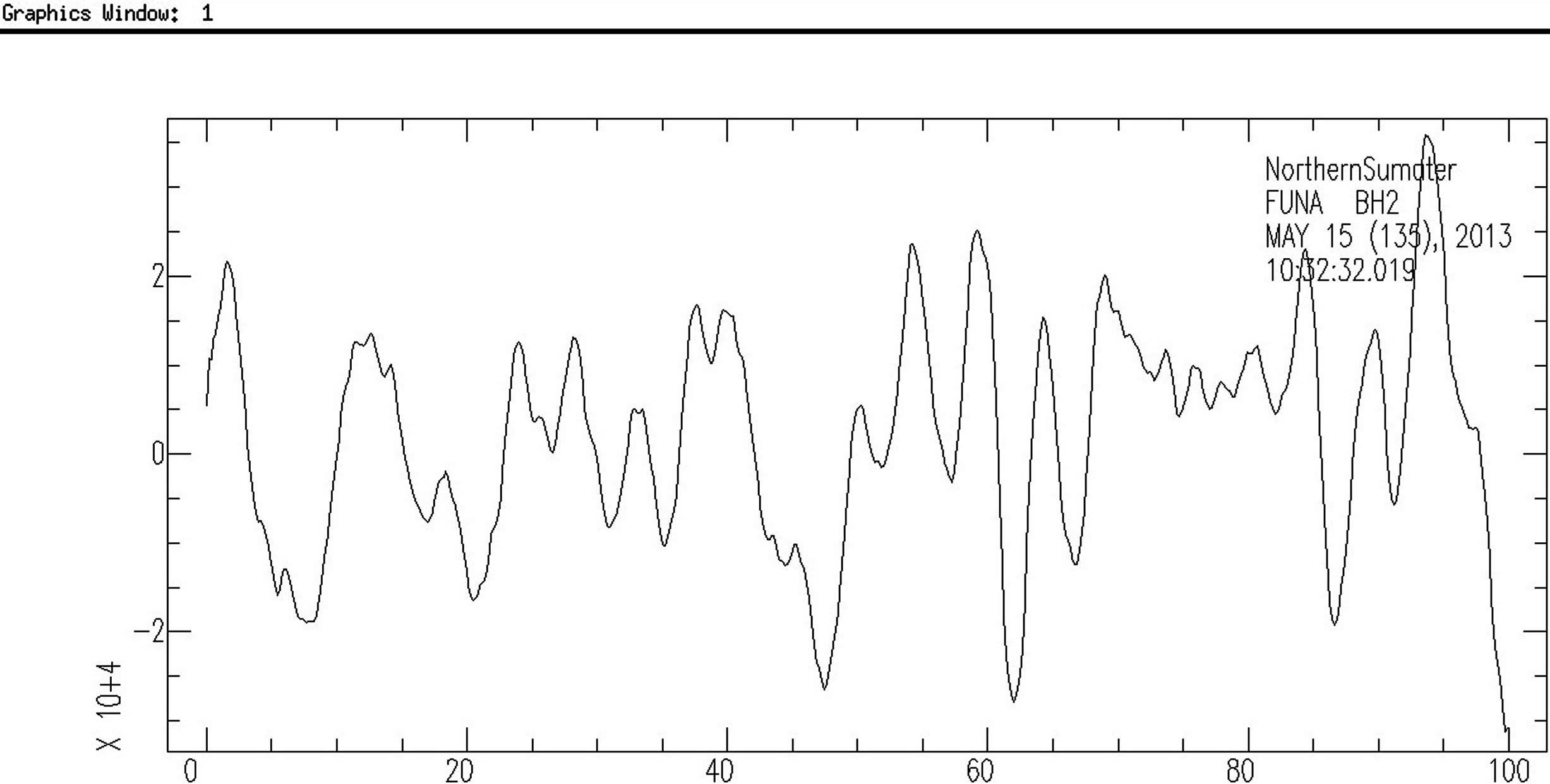 (a)
(a)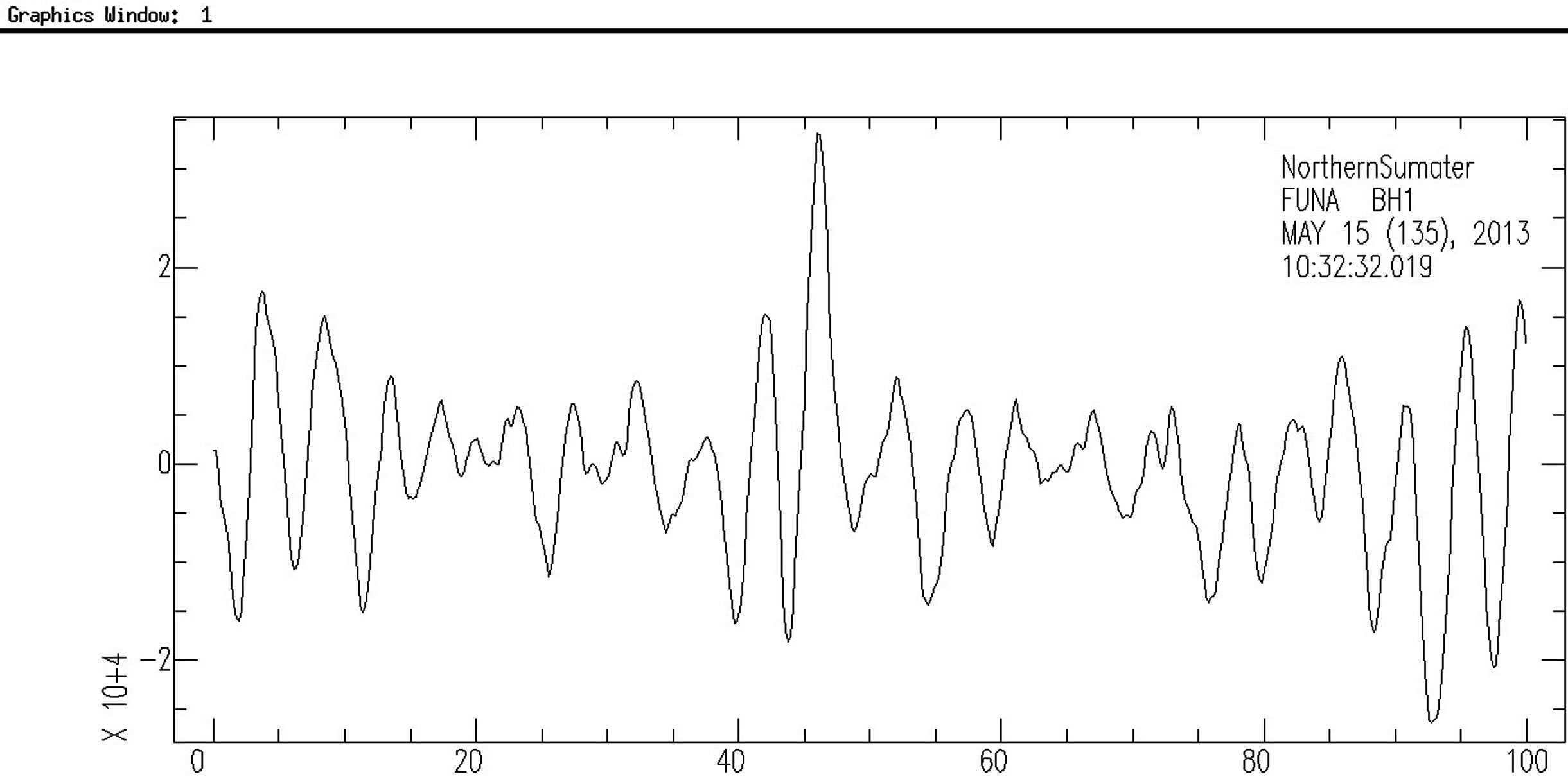 (b)
(b)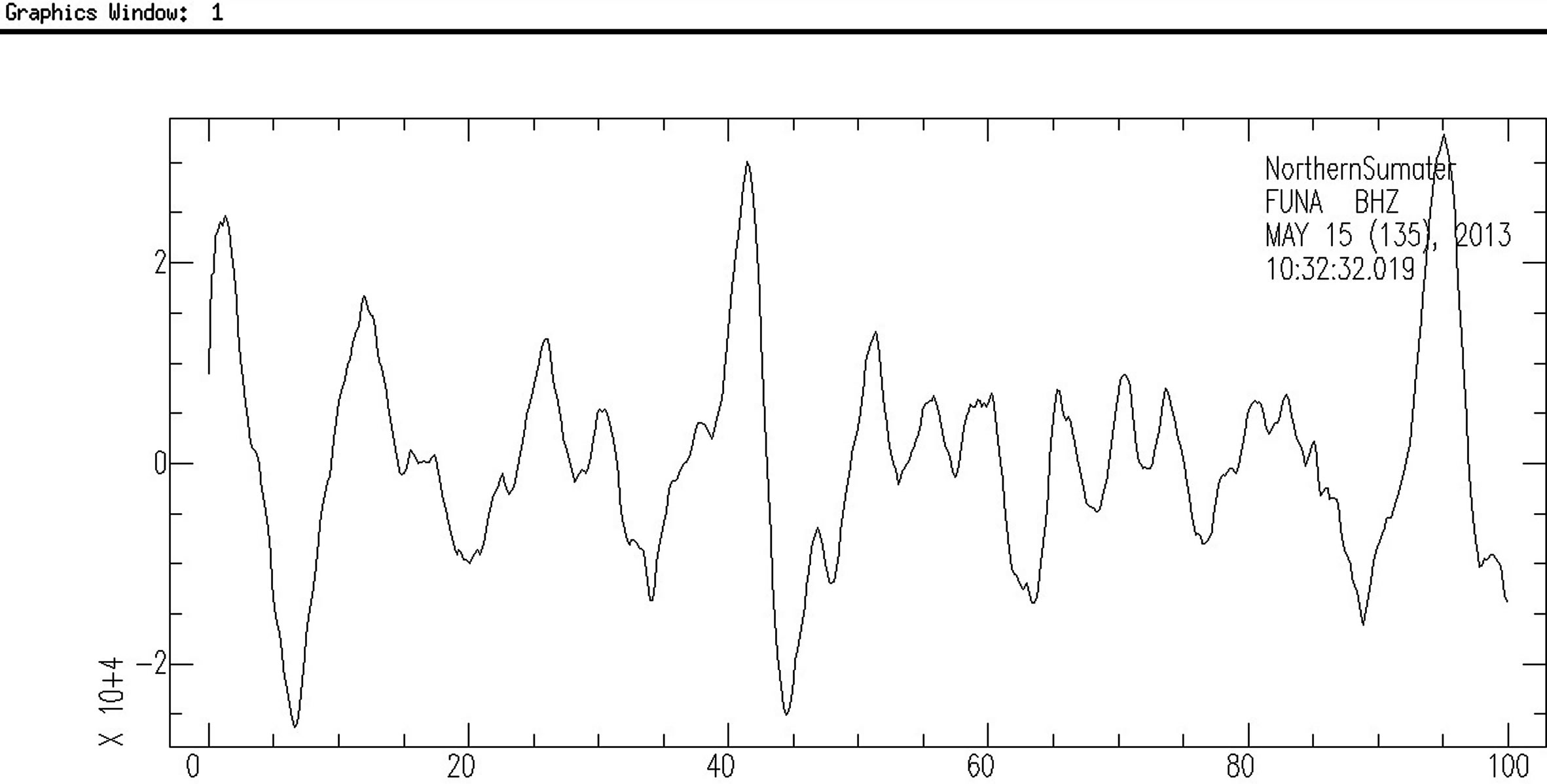 (c)
(c)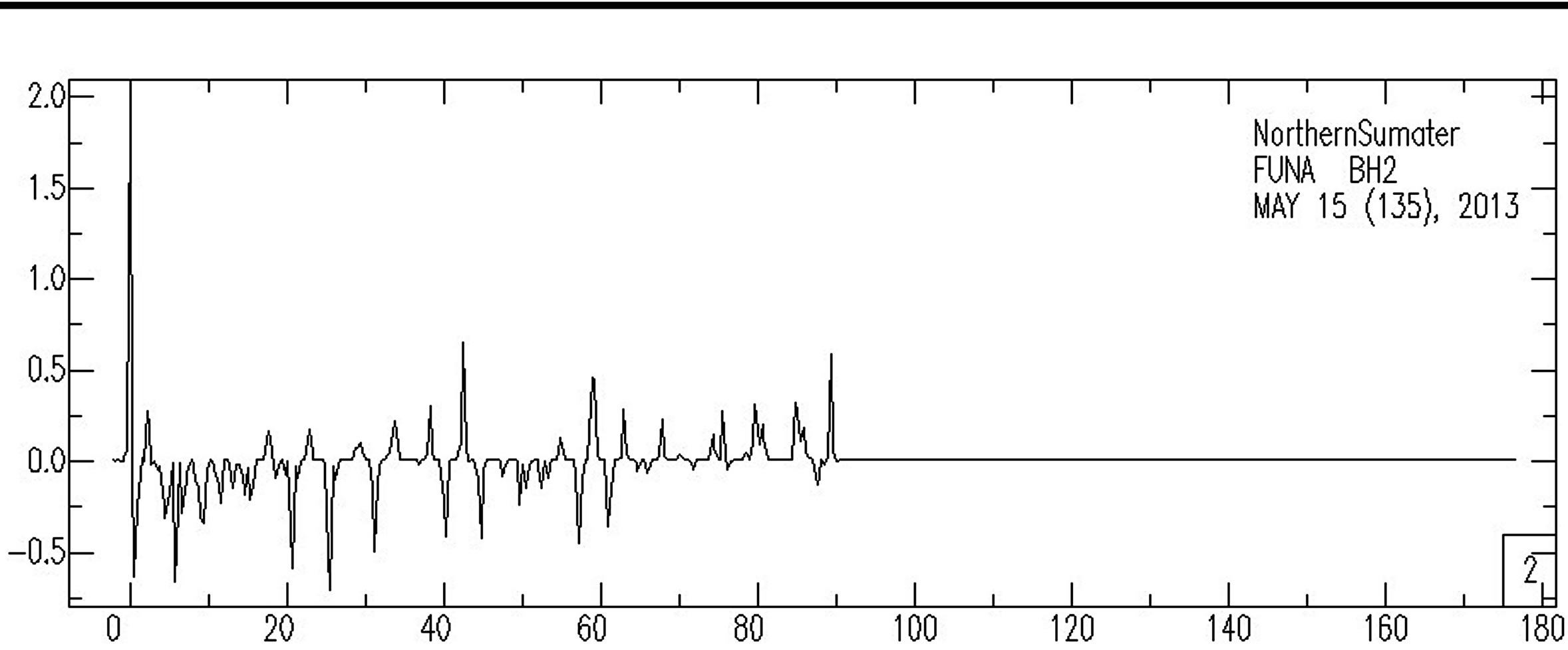 (d)
(d)
Figure 2. (a) and (b) show the two horizontal components of the seismogram, and (c) shows the vertical component. Iterative time domain deconvolution gives (d).
of the seismogram. The basis of the iterative time domain deconvolution method [10] is least-squares minimization of the difference between the observed horizontal seismogram and a predicted seismogram. This is obtained by the convolution of an iteratively updated spike train and the vertical component of the seismogram. As a first step, the vertical component is cross-correlated with the radial component to estimate the lag of the largest spike in the receiver function. The spike amplitude can be obtained by solving a simple equation as illustrated in [11]. The current estimate of the receiver function is convolved with the vertical component of the seismogram and the procedure is repeated to estimate other lags and amplitudes. As new lags and amplitudes appear on the predicted receiver function, the misfit values between the predicted radial component and the observed radial component is reduced. In this method the maximum amplitude spikes are first extracted and then progressively smaller and less significant ones are extracted. The iterations are repeated till an acceptable level of misfit is achieved. The quality of the receiver function is determined by the closeness in the matching between the observed and the computed horizontal component for the corresponding receiver function. The advantage of iterative time domain deconvolution method over spectral division is that it is robust even in the presence of noise and the bandwidth does not seem to have an effect in the deconvolution process.
2.3. Stacking of Receiver Functions
The amplitude and the arrival times of the Ps phases generated because of the interfaces vary as a function of back azimuth, the distance between the source and the receiver along the great circle and the event depth. In most of the cases, the seismograms have a considerable amount of noise. One of the main reasons behind stacking is to increase the signal-to-noise ratio in the receiver function. However while stacking it is important to consider the ray parameter. Stacking of receiver functions is performed in narrow bins of 10 degrees of back azimuth [12]. Stacking over a narrow bin of back azimuth is better as it helps in the identification of phases in case of a rapidly varying structure. If R1(t), R2(t),∙∙∙Rn(t) are receiver functions, then the stacked receiver function Rs(t) is defined by Equation (2).
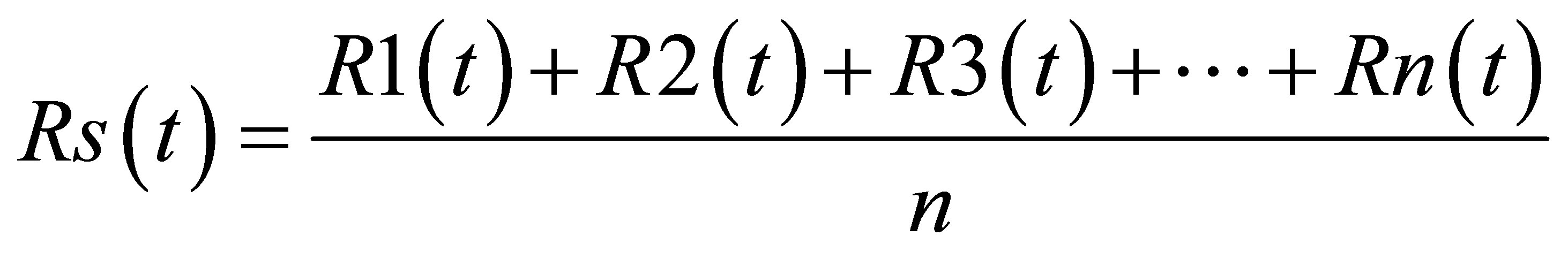 (2)
(2)
3. Geology of Funafuti
The Funafuti atoll is elongated in a near meridional direction due to it being situated on a volcanic zone [13]. The rock specimens that are commonly found on the atoll [14] are tabulated in Table 1.
The lagoon of Funafuti atoll is the largest in Tuvalu and has a north-south extension of 24.5 km and an eastwest extension of 17.5 km. The area of the lagoon is 275 km2 and extends down to 52 m. The lagoon is submerged with reefs. The cross section of the atoll suggests that there are primarily three foundation rocks [15]. The first and the topmost layer is the reef and lagoon calcareous deposits. The second could be firm carbonate rocks or equivalently volcanic rocks. The third layer is mainly oceanic crust and composed with basaltic rocks.
The western side of the Funafuti atoll, has larger and bigger pebbles of pumice stones as compared to the eastern side. This is attributed to the Carolinian Monsoon current. There is a West-North-West current that prevails in Funafuti during the trade-wind season and an easterly current during other seasons. The entire coastline of Funafuti is affected by erosion [16]. Erosion dominates deposition and the atoll is losing its beaches at a very rapid pace.
4. Estimating the Crustal Thickness of Funafuti
The principle used in estimating the crustal thickness of Funafuti is outlined in [17]. The arrival times of the various phases of the P wave namely Pp, Ps, PpSs, and PsPs was noted. In the naming of the phases except for the first arrival all capitals letters represent down going events and all small letters represent up going events of

Table 1. Rock specimens found in Funafuti atoll.
the corresponding phases. Except for the first two events all the other mentioned events produce a down going amplitude on the seismogram. The PpSs and the PsPs phases are recorded at the same time. Deconvolution of the vertical component with the two horizontal components ensures the creation of the receiver functions from which these phases can be easily observed. The time difference between these observed phases corresponds to the depth of the Moho from which these phases originnated. An initial range of the possible values of the depth and the Vp/Vs ratio for a given region must be assumed. The linear relationship between the observed time differences and these assumed values ensures that a best-fit result of the crustal thickness is obtained. This is achieved by plotting a contour map between Vp/Vs ratio versus the assumed depths. The region where the contours converge corresponds to the depth of the Moho and the Vp/ Vs ratio for the region.
The station Funafuti is located at latitude −8.52589˚ and longitude 179.19661˚. More than 54 different earthquake events were analyzed between 2008 and 2012 which occurred between 52.8˚N and 30.3˚N latitude and 132.1˚W and 102.9˚E longitude. The receiver functions were stacked and analysis was done with the assumption that the P wave velocity in the region was 6.0 km/s and the depth of the crust in the region lied between 5 km and 20 km and the Vp/Vs ratio was between 1.60 and 1.80. Figure 3 shows the results of the analysis.
The white region which is also the region where the contours seem to converge corresponds to the depth of the Moho and the Vp/Vs ratio for the given region. The places where the contours seem to touch are due to artifacts and should be ignored.

Figure 3. Contours of Vp/Vs ratio versus depth.
5. Conclusion
The depth of the Mohorovičić discontinuity for the Funafuti atoll obtained from receiver function analysis was found to be shallow at 11 km and the Vp/Vs ratio for the given region was around 1.75.
REFERENCES
- R. N. Jansson, “Receiver Function Modeling,” MS Thesis, University of Copenhagen, Copenhagen, 2008.
- H. Tiegan and D. A. Fiona, “Point Estimates of Crustal Thickness Using Receiver Function Stacking,” McGill Science Undergraduate Research Journal, Vol. 7, No. 1, 2012, pp. 21-27.
- Y. L. Chen, F. L. Niu, R. F. Liu, Z. B. Huang, H. Tkalčić, L. Sun and W. Chan, “Crustal Structure Beneath China from Receiver Function Analysis,” Journal of Geophysical Research, Vol. 115, 2010, Article ID: B03307.
- W. Lowrie, “Fundamentals of Geophysics,” Cambridge University Press, Cambridge, 2007.
- S. Stein and M. Wysession, “An Introduction to Seismology, Earthquakes, and Earth Structure,” Blackwell Publishing Ltd, Malden, 2003.
- M. P. Shearer, “Introduction to Seismology,” Cambridge University Press, Cambridge, 2009.
- C. A. Langston, “Structure under Mount Rainer, Washington, Inferred from Teleseismic Body Waves,” Journal of Geophysical Research, Vol. 84, No. B9, 1979, pp. 4749-4762. http://dx.doi.org/10.1029/JB084iB09p04749
- J. P. Ligorria and C. J. Ammon, “Iterative Deconvolution and Receiver Function Estimation,” Bulletin of the Seismological. Society of America, Vol. 89, No. 5, 1999, pp. 1395-1400.
- A. K. Pesce, “Comparison of Receiver Function Deconvolution Techniques,” MS Thesis, Massachusetts Institute of Technology, 2010.
- C. Escalante, J. Y. Gu and M. Sacchi, “Simultaneous Iterative Time-Domain Sparse Deconvolution to Teleseismic Receiver Functions,” Geophysical Journal International, Vol. 171, No. 1, 2007, pp. 316-325. http://dx.doi.org/10.1111/j.1365-246X.2007.03511.x
- M. Kikuchi and H. Kanamori, “Inversion of Complex Body Waves,” Bulletin of the Seismological Society of America, Vol. 72, No. 2, 1982, pp. 491-506.
- J. F. Cassidy, “Numerical Experiments in Broadband Receiver Function Analysis,” Bulletin of the Seismological Society of America, Vol. 82, No. 3, 1992, pp. 1453-1474.
- G. T. Bonney, “The Atoll of Funafuti: Borings into a Coral Reef and the Results. Being the Report of the Coral Reef Committee,” The Royal Society of London, London, 1904.
- T. Cooksey, “Rock Specimens from Funafuti,” Australian Museum, Sydney, 2012.
- A. Holmes and D. L. Holmes, “Principles of Physical Geology,” 3rd Edition, ELBS and Nelson, Hamshire, 1978.
- C. Xue and F. Malologa, “Coastal Sedimentation and Coastal Management of Fongafale, Funafuti Atoll, Tuvalu,” SOPAC Technical Report 221, 1995.
- L. Zhu and H. Kanamori, “Moho Depth Variation in Southern California from Teleseismic Receiver Functions,” Journal of Geophysical Research, Vol. 105, No. B2, 2000, pp. 2969-2980. http://dx.doi.org/10.1029/1999JB900322

