Journal of Flow Control, Measurement & Visualization
Vol.03 No.04(2015), Article ID:60449,6 pages
10.4236/jfcmv.2015.34015
Visualization of Double-Diffusive Convection and Unsteady Solidification on a Vertical Circular Cylinder
Kazuki Ohnishi, Shigeo Kimura, Takahiro Kiwata, Nobuyoshi Komatsu, Takaaki Kono
School of Mechanical Engineering, Kanazawa University, Kanazawa, Japan
Email: skimura@se.kanazawa-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2015; accepted 27 August 2015; published 21 October 2015
ABSTRACT
This paper describes experimental results on the solidification process over the vertically positioned circular cylinder, placed in an aqueous solution of sodium nitrate, where the aqueous solution in the vessel is heated from the bottom. After the initiation of solidification by cooling the cylinder below the liquidus temperature, the pure ice formation on the cylinder causes the rejection of solute into the surrounding aqueous solution. The solute enriched vertical fluid layer over the ice then falls on the bottom of the vessel due to its higher density, and accumulates there. This process results in the formation of solute rich and hot horizontal layer (heavy layer), underlying the relatively cold but less concentrated fluid layer (light layer). As this process advances, however, because of the continuing influx of solute rich fluid, the lower heavy layer occupies more space, and the interface of the two layers rises slowly. The pH indicator method has been successfully employed in order to visualize the flows during this process. In this report, we document the evolution of both temperature and flow fields in the aqueous solution quantitatively, as the solidification progresses and the density discontinuity of the two layers rises.
Keywords:
Solidification, Flow Visualization, Double-Diffusive Convection, Vertical Cylinder, Heat Transfer

1. Introduction
In countries such as Japan, where conventional energy resources are very scarce, it is a matter of urgency to look for alternative energy sources other than fossil fuels. Fortunately the amount of potential energy from geothermal sources in Japan is ranked as the third in the world, only behind the United States and Indonesia [1] . The conventional geothermal energy taps heated brine stored in the fractured deep rock formation at high temperatures about 200˚C. However, with the progress of drilling technology, it would in future become possible to reach the depth of magma chambers. Extraction of thermal energy from molten magma is very attractive because of its extremely high temperature, i.e. greater enthalpy or exergy source, and it is the ultimate goal of geothermal energy utilization. One proposed method to extract heat from molten magma is to employ downhole coaxial heat exchangers (DCHE), where the system consists of borehole casing pipe and the insulated inner pipe inserted in the borehole. While the cold water descends the annulus, it is heated at extremely high temperatures. The heated water will be then recovered to the surface via inner insulated pipe [2] [3] . If the above mentioned energy extraction system is put in practice, however, it is important to predict the magma solidification process at the borehole heat exchanger. Because the solid layer formation causes the thermal resistance, controlling its thickness is absolutely essential for steady heat output from the downhole heat exchanger.
In order to simulate the magma solidification process on the outer surface of the DCHE in the magma chamber, we employed aqueous solution of sodium nitrate in a cubical vessel and the cooled vertical circular cylinder [4] [5] . The bottom of the vessel is kept at a constant temperature higher than that of liquidus. This heating condition provides a kind of thermal analogy of constant influx of heat from a large size of magma chamber. We are particularly interested in the formation and evolution process of horizontal layering structure appearing in the solution, as the solidification on the cylinder progresses. The lower layer has generally a property of higher concentration and temperature than that of the upper layer [6] -[8] . Such layered structure in the solution is important, since it means that the liquid phase initial conditions of temperature and concentration are significantly altered as the solidification progresses. Despite the fact that the layered structures are common in many doubly diffusive convection systems, their flow structures have not been well documented for this particular configuration. In the present report we present the detailed flow and temperature structures in the layered convecting aqueous solution, in a particular geometric and thermal configuration, i.e. the solidification over the vertical cylinder in aqueous solution of sodium nitrate.
2. Growth of Solid Layer on the Vertical Cylinder
It is instructive to review a simple heat transfer analysis on the growth of solid formed on a vertical cylinder, place in an infinite volume of liquid. It will demonstrate the significance of convection on the growth of solid phase. Supposing that a vertical cylinder of height H is cooled below the liquidus temperature, the axisymmetric and vertically averaged growth of solid layer thickness f can be expressed by
 , (1)
, (1)
where k, L, r, 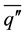 ,
,  , t are the thermal conductivity of solid, the latent heat, the radial coordinate measured from the center of the cylinder, the average convective heat flux on the solid surface, the vertically averaged temperature in solid varying only in radial direction and time respectively. The averaged convective heat flux on the surface of solidifying layer can be estimated by a Nusselt-Rayleigh number correlation proposed by LeFevre and Ede [9] , for instance. Once the average Nusselt number is known, the average convective heat flux can be expressed by
, t are the thermal conductivity of solid, the latent heat, the radial coordinate measured from the center of the cylinder, the average convective heat flux on the solid surface, the vertically averaged temperature in solid varying only in radial direction and time respectively. The averaged convective heat flux on the surface of solidifying layer can be estimated by a Nusselt-Rayleigh number correlation proposed by LeFevre and Ede [9] , for instance. Once the average Nusselt number is known, the average convective heat flux can be expressed by
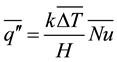 , (2)
, (2)
where 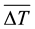 is the vertically averaged temperature difference between the solid surface and the liquid far from the surface.
is the vertically averaged temperature difference between the solid surface and the liquid far from the surface. 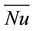 is a function of the Rayleigh number based on the height H and the Prandlt number, which implies that the convective heat flux
is a function of the Rayleigh number based on the height H and the Prandlt number, which implies that the convective heat flux 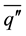 is a function of both
is a function of both 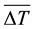 and H. It is clear that the layered structures appearing during the double diffusive convection in the liquid phase have a significant effect on the convective heat flux. Since each layer in the liquid possesses a unique temperature, concentration and height (thickness), the solid surface receives different convective heat fluxes from layer to layer, depending on which layer a portion of solid is in contact with. It should be also noted that the layered structure is not stationary, but it evolves as the solidification progresses. All the above discussions clearly show the importance of the evolution process of layered structure in the liquid in order to understand the growth of solid layer on the cylinder.
and H. It is clear that the layered structures appearing during the double diffusive convection in the liquid phase have a significant effect on the convective heat flux. Since each layer in the liquid possesses a unique temperature, concentration and height (thickness), the solid surface receives different convective heat fluxes from layer to layer, depending on which layer a portion of solid is in contact with. It should be also noted that the layered structure is not stationary, but it evolves as the solidification progresses. All the above discussions clearly show the importance of the evolution process of layered structure in the liquid in order to understand the growth of solid layer on the cylinder.
3. Experimental Apparatus and Procedure
3.1. Experimental Apparatus
The experimental apparatus is illustrated in Figure 1. A vessel containing aqueous solution is built with 15mm thick acrylic plates. The inner space has a 180 mm × 175 mm in horizontal widths and 180 mm in depth. All the walls of the vessel are practically insulated except for the bottom, where the copper plate is fitted and it is kept at a constant temperature by running temperature controlled brine (ethylene glycol solution). A circular copper cylinder of 30 mm in diameter and 135 mm in length is vertically positioned in the center of the vessel. The temperature-controlled cooling brine is circulated inside the cylinder, so that the cylinder surface is kept at any desired temperature below liquidus. Three thermocouples are installed on the cylinder surface in a few millimeters deep holes. Fifteen thermocouples are placed along the vertical line in order to monitor vertical temperature profiles in the aqueous solution. Six of them are positioned near the bottom with a 5 mm interval. The rest of them are installed at the higher positions with a 15 mm interval. One thermocouple is positioned at the center of bottom copper plate. The temperature data obtained by the thermocouples are stored automatically in the data-acquisition system. The 10% wt sodium nitrate solution is used to simulate 2-component molten liquid. A small amount of thymol blue (0.01% wt) is added for flow visualization. The DC power supply in the figure is used in order to perform pH indicator flow visualization.
3.2. Experimental Procedure and Flow Visualization
The experiment is started by introducing the same temperature brine (5˚C - 8˚C) in both bottom plate and the cylinder. After the system reaches an isothermal condition, which roughly takes 6 hours, the cold brine is introduced in the cylinder so that the vertically-averaged surface temperature becomes about −10˚C. At an early stage of process, the ice is formed uniformly over the cylinder, and the cold and solute enriched current descends along the cylinder. The current strikes the bottom, and then spreads radially over the bottom, during which it is heated and buoyant. The buoyant currents then ascend along the side wall. After several hours from the start, the layered structure is formed. Sixteen hours of temperature field measurements and flow visualizations are carried for sixteen hours, once every hour, in order to document the evolution of layered structure.
The flows in respective layers are visualized with thymol blue technique by Baker [9] . Three thin stainless wires are introduced from above, as illustrated in a right upper corner of the vessel in Figure 1. One of them works as anode, and the other two work as cathode by connecting to a power source. 1.5 V is applied between them. When a weak electrolysis is performed, the cathode wires color the neighboring solution dark blue. The
Figure 1. Experimental apparatus.
colored fluid parcels are then swept by neighboring flows and form dark streak lines. The streak line patterns are recorded by digital camera in order to document overall flow structures. Flow velocities are also determined by growth rate of streak length. The cathode wire is painted except a few bands of about 5mm width, which helps to produce clear thin streak lines, making for easy flow visualization.
Some considerations must be needed to guarantee the accuracy of the pH indicator method. Since the Reynolds number based on the electrode diameter (0.5 mm) is of the order of 1, the colored fluid from the electrode surface will be released in the wake without any flow separation, nor any vortex street. Therefore, the transversal wake thickness is kept as the order of 1mm. The viscous diffusion time across this thickness is of the order of one second. This guarantees that the velocity in the electrode wake will quickly become the same as the neighboring fluid velocity. The other point that we have to take into consideration is the mass diffusion, which blurs the streak images. Due to the fact that the mass diffusion time across 1 mm distance will be of the order of 1000 sec, and that the photographic record has been conducted with a 5 second interval, it can be said that the growth rate of streak line will be hardly affected by the mass diffusion.
4. Experimental Results and Discussions
In Figure 2, we show the snapshots of streak lines at four different times after the start of experiment. The corresponding vertical temperature profiles are also shown in Figure 3. The experimental conditions are 10wt% sodium nitrate solution, −10˚C cylinder surface temperature, and 5˚C bottom surface temperature. During the early stages of solidification, a highly concentrated solute layer is formed over the bottom surface, due to salt rejection from the solid phase and the downwards currents along the cylinder. This salt-enriched layer, on the other hand, is subject to constant heating from the bottom, which eventually destabilizes the layer, causing development of multi-layered flow structure within it, as seen in Figure 2(a). At four hours after the start of experiment, the aqueous solution is divided into two layers. The streak patterns are depicted in Figure 2(b), and the corresponding temperature profile is shown in Figure 3. From these two, it is clear that the cold fluid layer overlays the hot fluid layer. In the both layers, the convecting flows are obviously in the counter clockwise direction. Therefore, near the layer interface, it is right to left in the upper layer, and left to right in the lower layer in the Figure 2. In further advancement of the process, the solid phase contacting with the upper layer does not grow radially, but it shrinks in height due to the rise of the lower layer. The constant ice thickness indicates that the convective heat transfer from the liquid to the solid takes place without any phase change. The cold downwards currents are visible along the ice surface, but they eventually change their directions to the horizontal,
Figure 2. Visualization of streak lines at different times by pH indicator method. The photographs were shot from the back of the illustrated experimental apparatus in Figure 1. Therefore, those photographs are showing the right half of the illustration of Figure 1.
Figure 3. Vertical temperature profiles at different times (the bottom temperature is 5˚C).
advancing radially over the interface between the two layers. On the other hand, the warm and salt-rich lower layer starts melting the lower portion of ice over the cylinder. Since the ice thickness in the lower layer does not change significantly over a period of time 8 and 16 hours after the start of the experiment, it seems that there exists an equilibrium thickness, determined by the balance between the convecting heat flux and the radially conductive cooling. Comparing the streak patterns in Figures 2(b)-(d) and Figure 3, it is clearly seen that the interface positions indicated by the presence of horizontal counter flows exactly correspond to those of the steep temperature slopes. It should be noted that the lower layer is occupied with a well-mixed uniform temperature solution in the late stage of the experiment.
The horizontally and radially advancing flow velocities in the upper layer, covering over the interface, are shown in Figure 4 for two different bottom temperatures. A general trend is the same in both conditions. The velocities are less than 1mm/s. The velocities increase linearly up to a time period of 8 or 9 hours after the start of the experiment. Beyond that the velocities start decreasing. The temperature increase in the upper layer in the early stages is probably responsible for the greater Rayleigh numbers, and hence the increasing velocities. After 8-9 hours, the temperature increase in the upper layer stops, but the layer’s vertical thickness continues to decrease, which results in decrease in the Rayleigh number, resulting in a decrease in velocities.
The horizontally and radially advancing flow velocities in the upper layer, covering over the interface, are shown in Figure 4 for two different bottom temperatures. A general trend is the same in both conditions. The velocities are less than 1mm/s. The velocities increase linearly up to a time period of 8 or 9 hours after the start of the experiment. Beyond that the velocities start decreasing. The temperature increase in the upper layer in the early stages is probably responsible for the greater Rayleigh numbers, and hence the increasing velocities. After 8-9 hours, the temperature increase in the upper layer stops, but the layer’s vertical thickness continues to decrease, which results in decrease in the Rayleigh number, resulting in a decrease in velocities.
Figure 5 shows how the interface between the two layers ascends as the process advances, for four different bottom heating conditions. Again a common trend can be identified as a linear growth of the height of the interface with time, particularly beyond the time of 5 hours after the start of the experiment. The growing rates are larger for higher bottom temperatures. In fact the upper layer disappears in 14 hours after the initiation, when the heating bottom temperature is at 8˚C.
5. Concluding Remarks
Evolution of double diffusive convection system associated with a solidification process over a vertical cylinder placed in sodium nitrate aqueous solution has been investigated. The aqueous solution fills a rectangular box, and the vertical cooling cylinder is placed at the center. Two convecting layers are formed in four hours after the
Figure 4. Horizontal convective velocities in the upper layer over the interface.
Figure 5. Time-development of the interface positions measured from the bottom.
start of the experiment, where cold and low concentration solution (light layer) overlays that of warm and high concentration (heavy layer). The interface positions between the two layers ascend until the lower convecting layer occupies the entire space. The pH indicator method has been successfully employed in order to visualize the flow fields and to quantify the velocities. It has been verified that the interface between the two layers corresponds exactly to the position where the steep temperature slope is observed. The convection velocities in the upper layer are in the order of 1 mm/s. This order of velocity magnitude is comparable with naturally convective velocity along the cold plate, where the temperature difference is several degrees in Celsius. Due to the difference in temperature and concentration between the two layers, it should be noted that the ice over the cylinder has also different thickness depending on which layer the ice is in contact with.
Acknowledgements
The second author (S.K.) thanks support by JSPS KAKENHI Grant number 25420153.
Cite this paper
KazukiOhnishi,ShigeoKimura,TakahiroKiwata,NobuyoshiKomatsu,TakaakiKono, (2015) Visualization of Double-Diffusive Convection and Unsteady Solidification on a Vertical Circular Cylinder. Journal of Flow Control, Measurement & Visualization,03,154-160. doi: 10.4236/jfcmv.2015.34015
References
- 1. Yasukawa, K., Noda, T., Muraoka, H., Adachi, M., Matsunaga, I. and Ehara, S. (2010) Long-Term Prospects of Geothermal Energy Uses and Their Environmental Effects in Japan. Proceedings of World Geothermal Congress 2010 (CD-ROM), Bali, Indonesia, 25-29 April 2010, 4 p.
- 2. Hardee, H.C. (1981) Convective Heat Extraction from Molten Magma. Journal of Volcanology and Geothermal Research, 10, 175-193. http://dx.doi.org/10.1016/0377-0273(81)90061-5
- 3. Morita, K. and Tago, M. (2000) Operational Characteristics of the GAIA Snow-Melting System in Ninohe, Japan. Geo-Heat Center, 21, 5-11.
- 4. Huppert, H.E. and Turner, J.S. (1981) A Laboratory Model of a Replenished Magma Chamber. Earth and Planetary Science Letters, 54, 144-152. http://dx.doi.org/10.1016/0012-821X(81)90075-3
- 5. Huppert, H.E. and Sparks, R.S.J. (1984) Double-Diffusive Convection Due to Crystallization in Magmas. Annual Review of Earth and Planetary Sciences, 12, 11-37. http://dx.doi.org/10.1146/annurev.ea.12.050184.000303
- 6. Worster, M.G. (1986) Solidification of an Alloy from a Cooled Boundary. Journal of Fluid Mechanics, 167, 481-501. http://dx.doi.org/10.1017/S0022112086002938
- 7. Huppert, H.E. (1990) The Fluid Mechanics of Solidification. Journal of Fluid Mechanics, 212, 209-240. http://dx.doi.org/10.1017/S0022112090001938
- 8. Wettlaufer, J.S., Worster, M.G. and Huppert, H.E. (1997) Natural Convection during Solidification of an Alloy from Above with Application to the Evolution of Sea Ice. Journal of Fluid Mechanics, 344, 291-316. http://dx.doi.org/10.1017/S0022112097006022
- 9. Baker, D.J. (1966) A Technique for Precise Measurement of Small Fluid Velocities. Journal of Fluid Mechanics, 26, 573-575. http://dx.doi.org/10.1017/S002211206600140X






