Journal of Flow Control, Measurement & Visualization
Vol.03 No.03(2015), Article ID:58433,10 pages
10.4236/jfcmv.2015.33011
Flow Properties of Ultra-Fine Bubble Mixtures Passing through Micro-Apertures
Akiomi Ushida1, Tomiichi Hasegawa2, Takatsune Narumi1, Itaru Kourakata3, Yoshinori Nakamoto4
1Faculty of Engineering, Niigata University, Niigata-shi, Japan
2Niigata College of Technology, Niigata-shi, Japan
3Institute for Research Collaboration and Promotion, Niigata University, Niigata-shi, Japan
4TECH CORPORATION Co. Ltd., Hiroshima-shi, Japan
Email: ushida@eng.niigata-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 2 July 2015; published 29 July 2015
ABSTRACT
The flow properties of fine bubble mixture flows are investigated and reported. Few previous studies have focused on ultra-fine bubble (UFB) mixtures, which contain sub-micrometer sized bubbles. In this study, UFB mixtures of water and glycerol solution are passed through micro-sized slits and capillaries, and the resultant pressure drops are evaluated in comparison with those for water and aqueous glycerol alone. The experimentally measured pressure drop for slits (≤51 μm) and capillaries (≤81 μm) is less for UFB mixtures than for water and aqueous glycerol alone. This phenomenon is considered in terms of interface behavior and attributed to the electric interaction between an electric double layer and the UFBs. Furthermore, numerical observation for slip wall conditions is conducted, and the results for UFB mixtures agree with the predicted values for slip wall conditions.
Keywords:
Micro-Aperture, Ultra-Fine Bubble, Water, Glycerol, Pressure Drop

1. Introduction
Many studies have been carried out in recent years on drag reduction, flow property, cleaning and washing effect, and water purification of fine bubble (FB) mixtures, which contain sub-millimeter sized bubbles. Sanders et al. [1] investigated drag reduction of FB in high Reynolds number mixtures with bubbles near the surface on which the boundary layer forms, and found that the effect was lost when wall shear induced the migration of the bubbles from the wall surface. Shen et al. [2] reported friction reduction in a turbulent water channel flow using a nitrogen/water FB mixture. Murai et al. [3] studied skin friction reduction in ship walls using relatively large FBs, and reported the dependency of average skin friction on bubble size under intermediate bubble size conditions. Mohanarangam et al. [4] numerically observed the phenomenon of drag reduction by the injection of FBs in the turbulent boundary layer by using a Eulerian-Eulerian two-fluid model, and discussed the change in mean velocity profiles, void fraction and turbulence modification as the corresponding gas injection rates were changed. Tom and Liu [5] conducted experiments on the pressure drop in high-viscosity liquids containing FBs. Nouri et al. [6] investigated the effect of FBs on the pressure drop generated by frictional losses in upward pipe flows, and reported a reduction in pressure drop. The above studies described “turbulent drag reduction” for FB mixtures in relatively high Reynolds numbers. For instance, Reynolds number ≤ 2.1 × 108 (Sanders et al. [1] ), Reynolds number ≤ 1.0 × 107 (Shen et al. [2] ), Reynolds number ≤ 1.7 × 104 (Murai et al. [3] ), and Reynolds number ≤ 3.0 × 103 (Nouri et al. [6] ) were used. Additionally, their used FB sizes were relative large scales (Although a minimum particle diameter was 44 μm [2] , almost all FB sizes were more than 100 μm).
Moreover, regardless of the theme of frictional resistance, studies on the flow properties were reported. Yanuar et al. [7] conducted an experimental study on identifying the effects of injected FBs on a large scale boat- type model. Choi et al. [8] observed the flow properties of FB mixtures (mixed in surfactant solutions) passing through porous media. Jovanovića et al. [9] measured the pressure drop in liquid-liquid (viz. water-toluene and ethylene glycol/water-toluene) slug flows through micro-sized channels and capillaries.
Furthermore, development of the applications using FBs is as follows. Miyamoto et al. [10] developed a new cleaning technology that uses FBs to reduce the environmental impact and cost of industrial cleaning, and found that the cleaning rates using FBs were greatly improved compared with using normal bubbles. Liu et al. [11] and Versluis [12] also conducted similar industrial cleaning tests on FB mixtures. Lee et al. [13] observed the influence of FBs on human skin cleansing. Ushida et al. [14] measured the washing rates of FB mixtures applied to cloth and found that the resultant washing rates were larger when using FB mixtures than water alone. Burns et al. [15] examined several factors that affected the size of FBs produced by the processes of electroflotation, dissolved air flotation, and a relatively new method known as electrostatic spraying. Fujiwara et al. [16] developed FB generation techniques proposed in previous studies. Yamada et al. [17] discussed the relationship between bubble size populations and their effects on oxygen supply. Tsuge et al. [18] investigated the bactericidal effect of ozone FBs on Bacillus subtilis by changing parameters such as the outlet pressure of the pump, elapsed time, concentration of fed and dissolved ozone, and FB formation method. Ohnari et al. [19] investigated the water purification and recovery of oyster cultures in a bay by using FBs. Zhang et al. [20] observed a novel ozonation system based on FB technique was applied as a disinfection process. Ikeura et al. [21] investigated effect of ozone FBs treatment on the removal of residual fenitrothion and reported the continuous bubbling ozone FBs treatment was more effective than the non-bubbling ozone FBs treatment at reducing the residual fenitrothion. Numerous interesting applications of FB mixtures have been developed and are used in several fields.
Many previous studies of FB mixtures have investigated the shear flows in pipe and channel flows. However, there are few reports of elongational flows, such as orifice flows and slit flows, and even fewer studies of ultra- fine bubble (UFB) mixtures in elongational flows. Especially, the uses of characteristic length for ≤100 μm and of UFB mixtures were limited. In the present study, the pressure drop in UFB mixtures passing through small slits and capillaries (micro-apertures) was measured, and their flow properties were investigated. Additionally, the effects of UFB mixtures on the flow properties of water and glycerol solutions were clarified.
2. Experimental Setup
2.1. Small Slit
Table 1 shows the specifications of the small slits used in our experiments. To construct a slit, two pieces of stainless steel (SUS304) of thickness H = 200 μm were attached to an aluminum base plate (Figure 1). The slit width, B, was in the range of 39 to 113 μm, and the slit length, W, was 20 mm. The slits were almost the same as those used in previous study [22] .
2.2. Experimental Apparatus
Figure 2(a) and Figure 2(b) show an overview of the experimental apparatus. The experimental apparatus
Table 1. Details of the slits.
Figure 1. Schematic of the slits.

Figure 2. Schematic of experimental apparatus for measuring pressure drops in case of (a) slit flows and (b) capillary flows.
shown in Figure 2(b) was described in the “capillary flows” section. A syringe pump (JP-H1, Furue Science Co. Ltd., Japan) was charged with a test fluid, which was then fed into a channel at a constant flow rate, Q. A slit was placed at the end of the channel, with the liquid passing through the slit as a jet. Pressure ports were built into an acrylic channel (inner diameter, 25 mm; length, 180 mm) and acrylic vessel. The differential pressures were measured as pressure drops, Δp, by using a pressure transducer (SPD-12, Tsukasa Sokken Co. Ltd., Japan). Pressures of 500 Pa, 10 kPa, 100 kPa, and 500 kPa were used, corresponding to the Δp values. For pressures of more than 500 kPa, Bourdon pressure gauges (0.5 and 1.0 MPa, Yamamoto Keiki Instrument Co. Ltd., Japan) were used after calibration.
2.3. Test Fluids
The test fluids used in this study were as follows: an aqueous mixture containing 1.0 vol% UFBs (hereinafter called UFB water) and deionized water (electric conductivity = 0.055 μS∙cm−1; GSR-200, ADVANTEC Co. Ltd., Japan; hereinafter simply called water). In addition, aqueous solution of glycerol (1:1, glycerol/water w/w) and mixed UFB glycerol solution were used (hereinafter, glycerol and UFB glycerol, respectively). The UFB mixtures were prepared with a UFB generator (Nano Aqua MN-20, TECH CORPORATION Co. Ltd., Japan) by means of a high swirl flow. The resulting mixtures contained 1.0 vol% UFBs, as per the settings of the UFB generator, and were measured by a nanoparticle analyzer (NanoSight LM1-HS, Quantum Design Japan Co. Ltd., Japan). Furthermore, the UFB diameter, also measured by the nanoparticle analyzer, was approximately 110 nm (peak diameter, 70 nm) as shown in Figure 3 (number density, Nb, versus particle diameter, Db).
The density, ρ, of the UFB mixtures was measured on the Baume scale, and found to be 0.99 times the density of water and glycerol. This density was the averaged value of numerous measurements in the temperature range of 5˚C to 30˚C.
The viscosity, μ, was measured by using a capillary viscosity meter, which measures the pressure drops and flow rate assuming Hagen-Poiseuille flows. Figure 4 shows the measured viscosity (Equation (1)), μ, plotted against shear rate on the wall, SRw.
 (1)
(1)
Good agreement between the experimental values and the predictions of Newton’s Law was observed. The all error bars (= 13%) were estimated by individual measurement error, flow rate = 1%, diameter = 1%, and pressure drop = 8%. The viscosity of UFB water was found to be the same as the viscosity of water (μ = 1.0 × 10−3 Pa∙s). Moreover, as shown in Figure 4, the viscosity of glycerol and UFB glycerol was 10 times that of water. Thus, μ = 1.0 × 10−2 Pa∙s was estimated in glycerol and UFB glycerol.
Figure 3. Number density, Nb, plotted against particle diameter, Db, for the prepared UFB mixtures.
Figure 4. Relationship between estimated viscosity, μ, and shear rate on wall, SRw, assuming Hagen-Poiseuille flow.
3. Experimental Results
The measured Δp is expressed as a dimensionless pressure drop, K (Equation (2)), and the Reynolds number is given by Re (Equation (3), where V is the mean velocity passing through slits). The test fluid temperatures, T, are shown in the figures along with the results.
 (2)
(2)
 (3)
(3)
Figures 5(a)-(d) show the results for water, UFB water, glycerol, and UFB glycerol passed through small slits. The vertical axis shows K, and the horizontal axis shows Re. The numerical predictions of the Navier-Stokes equations are also shown for comparison [22] . The experimental errors (=29%) were estimated by individual measurement errors, flow rate = 1%, slit width = 5%, and pressure drop = 8%. Flow direction was shown in Figure 1. However, agreement between the resultant pressure drops in the present flow direction and those in the backward direction was obtained (Figure 5(d)). Thus, the effect of inlet regions and geometry in upstream was negligible. When B is larger than 81 μm (Figure 5(a) and Figure 5(b)), the experimental results for all test fluids agreed with the predictions of the Navier-Stokes equations. Thus, for a slit width of more than 81 μm, the pressure drops in the UFB mixtures were the same as in water and glycerol alone. However, when B was less than 51 μm, the resultant pressure drops for the UFB mixtures (UFB water and UFB glycerol) were lower than those of water and glycerol alone (Figure 5(c) and Figure 5(d)). Compared with the experimental results for water and glycerol alone, the resultant UFB mixtures were less than those of water and glycerol alone.
Figure 5. Dimensionless pressure drops, K, versus Reynolds number, Re, in slit flows. The data of (a) B = 113 μm and (b) B = 81 μm agreed with the predicted values. For (c) B = 51 μm and (d) B = 39 μm, agreement between the experimental results and the predictions was not obtained.
4. Numerical Investigation of Slip Conditions
Pressure drops of UFB mixtures were less than those of water and glycerol alone. In this section, influence of slip was discussed. To examine the wall slip, numerical simulation was carried out for slit flows under slip conditions. The two-dimensional dimensionless Navier-Stokes equations and continuity equation are as follows.
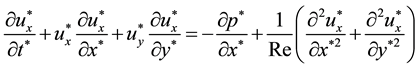 (4)
(4)
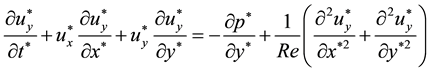 (5)
(5)
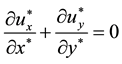 (6)
(6)
Here, asterisks indicate dimensionless parameters, and 

Figure 6(a) shows the numerical model. Numerical conditions are almost same for the previous study [22] . The width of the channel upstream and downstream of the slit are 100B, the upstream and downstream lengths are 100B and 200B. The grid number is 1024 in each direction. The following boundary conditions are adopted: (a) two-dimensional Poiseuille flow exists at the inlet boundary; (b) the pressure and velocity in the y* direction is zero at the outlet boundary; (c) the y* component of the velocity is zero along the center line; and (d) all velocity gradients are zero at the wall (perfect slip conditions). Figure 6(b) shows the dimensionless pressure drop
Figure 6. Dimensionless pressure drops, K, plotted against Reynolds number, Re, for slip phenomena. (a) Schematic illustration of numerical simulationand (b) numerical prediction and experimental data.
versus Reynolds number for the present numerical results (broken line) and the experimental results for 51 μm. The calculated predictions nearly agree with the experimental results for a slit width of 51 μm. These results were suggested the possibility of slip phenomena.
5. Discussion
Pressure drops were measured when UFB water and UFB glycerol having an average bubble diameter of approximately 110 nm were passed through small slits. The experimentally measured pressure drops were lower for UFB water than for water, and UFB glycerol had lower pressure drops than glycerol when slits of less than 51 μm were used. In previous studies, Hasegawa et al. [23] reported the possibility that water flow through a micro-aperture is elastic, but in the case of UFB mixtures containing only air, it is not thought that the results can be explained in terms of elasticity. In research employing Re values similar to those in this study, Ushida et al. [24] noted that surfactant molecules behave like polymer chains as a result of electric interactions, and are therefore able to exhibit a phenomenon similar to elasticity. Additionally, compared with the UFB size, the slit width was much larger; the ratio between averaged value of Db and smallest slit width was 2.82 × 10−3. Thus, size effect of slit width was negligible.
However, the pseudo-laminarization effect (maintaining the laminar flow in transition regions) of FB mixtures in capillary flows was reported in previous studies. Serizawa et al. [25] measured pressure drops of FB mixtures in capillary flows with inner diameters of 6 mm. Ushida et al. [26] conducted similar experiments in smaller capillary flows with inner diameters of <1 mm. These studies discussed the void fraction of FBs, size effect (relation to the diameter), and surface tension between the FB mixtures and capillary wall. They observed no relationship between pseudo-laminarization and bubble size effect, and the electric interaction was discussed by Ushida et al. [26] . The present results are similar to the previous results in terms of electric interactions, but we consider the results from a slightly different perspective. In general, solid wall surfaces carry negative charge in water; and this phenomenon comes from zeta potential. The liquid around the slit carries positive charge (hydrogen ions; H+) due to the electrical double layer [27] . Moreover, FBs and UFBs have also been found to carry negative charge in aqueous solution [28] . Figure 7 shows a schematic diagram of UFB mixture flows near a slit wall. Thus, in electrical terms, bubbles that carry a negative charge can be regarded as a flow passing a positively charged wall surface. In this case, an electric attraction occurs, and the bubbles adhere to the wall surface. A gas phase forms near the surface of the slit wall, and the UFB mixtures flow along this gas phase. Owing to the presence of the gas phase, a wall slip phenomenon occurs between the wall surface and the liquid surface. Furthermore, the effect is expected to become more pronounced as the thickness ratio, H/B, increases, that is, as the wall surface along which the liquid flows becomes longer relative to the slit width. Moreover, the pressure drop reduction on the slip wall was reported [29] , and the electric effect of the interaction between the water structure and interfacial charges was discussed in previous studies [30] . Thus, the present discussions are consistent with these studies.
It thus follows that the electric effect increases as the effect of the wall surface increases, and this is consistent with the results shown in Figures 5(a)-(d). In addition, agreement between the resultant pressure drops and the predictions was observed when using a slit width of 81 μm. This is attributed to the thickness of the electrical double layer being approximately 1.0 μm [31] and the region subject to the electric effect thus being small relative to the size of the slit (the larger the thickness ratio, the bigger the electric effect). The experimental results also are arranged in order of strain rate, and the influence of strain rate was discussed. Figure 8(a) and Figure 8(b) show Δp versus apparent strain rate, SRapp (Equation (7)).
Figure 7. Schematic of the interface between UFBs and slit wall.

In Figure 8(b), the differences between water results and those of UFB water occur for SRapp > 1 × 105 s−1. However, in Figure 8(a), SRapp ranges from 1 × 102 to 1 × 105 s−1. This is why the differences did not appear.
6. Frictional Coefficient of Pipe
Flow properties were investigated in the slit flow of the UFB mixtures and explained in terms of wall slip. Therefore, two types of capillaries were employed to investigate the effects of slip. The stainless steel (SUS304) capillaries were 125, 108, 81, and 73 μm in diameter. The frictional coefficient, λ, was investigated for water, glycerol, UFB water, and UFB glycerol. Figure 2(b) shows the experimental setup. Δp was measured, and λ was estimated using the following equation.

Here, Dc is the diameter of the capillary and Lc (= 50 mm) is the distance between the two pressure ports (distance between A and B, Figure 2(b)). Vc is the mean velocity of the liquid through the capillaries. The syringe pump and pressure transducer used in this experiment were the same as in the slit flow experiments. Figure 9
Figure 8. Plotting pressure drops, Δp, against apparent strain rate, SRapp, for observing the influence of strain rate. For (a) B = 81 μm, agreement between the resultant pressure drop andthe prediction was obtained. Experimental data of (b) B = 51 μm did not agree with the prediction in relatively high strain rate (>1.0 × 105 s−1).
Figure 9. Frictional coefficient of pipe, λ, as a function of Reynolds number, Re, in capillary flows. For Dc = 73 μm, the experimental values were less than those of the prediction of Hagen-Poiseuille flow.
shows the experimental results for λ versus Re (= ρVcDc/μ). The experimental errors (= 13%) were estimated by individual measurement errors, flow rate = 1%, diameter = 1%, and pressure drop = 8%.The λ values of all results agreed with the prediction of Hagen-Poiseuille flow except for UFB mixtures in the capillary with an inner diameter of 81 and 73 μm, in which case the discrepancy was less than 10%. It was found that the properties of the liquids (e.g., elasticity) were not affected in the case of capillary flow [32] . In fact, the reduction (Dc = 81 and 73 μm, UFB water and UFB glycerol) was caused by wall slip phenomena in the same case of the slit flows. These results strongly suggested that UFB mixtures exhibit pressure drop reduction effect. However, these results were suggested to a relatively limited Re range; 1.0 × 102 ≤ Re ≤ 2.0 × 103 in slit flows and 1.0 × 102 ≤ Re ≤ 6.0 × 102 in capillary flows. Thus, it is necessary to conduct the further delineation.
7. Concluding Remarks
The pressure drop in UFB water and UFB glycerol passing through small slits was measured, and the following results were obtained by comparing water and glycerol alone.
・ For a slit width of more than 81 μm, the resultant pressure drops in the UFB mixtures were the same value as in water and glycerol alone. When using a slit width of less than 51 μm, the pressure drop was lower in UFB mixtures than in water and glycerol alone.
・ Through a comparison between numerical and experimental results, the results for UFB mixtures were found to be consistent with wall slip. Furthermore, the influence of slip phenomena was discussed in terms of interface phenomena. UFBs are thought to adhere to the wall surface, forming a gas phase, which resulted in wall slip.
・ For capillary flow (inner diameter, 81 and 73 μm), the frictional coefficient of pipe for UFB mixtures was less than that for a Hagen-Poiseuille flow.
Acknowledgements
This study was partially supported by JSPS KAKENHI Grant-in-Aid No. 26820041 and Sasaki Environmental Technology Foundation. We thank Mr. Ryuichi Kayaba, Mr. Hiroshige Uchiyama, Mr. Naoyuki Takahashi, Mr. Shotaro Murao, Mr. Takahiro Koyama, Ms. Maiko Watanabe, and Mr. Taisuke Sato for technical assistance in carrying out experiments. We also thank Mr. Hiroshi Ono, Mr. Yoshinori Nakano, and Mr. Rikiya Oka for setting up the UFB generator (Nano Aqua MN-20, TECH CORPORATION Co. Ltd., Japan). Furthermore, we would like to gratefully thank editors and reviewers for help in significantly improving the manuscript.
Cite this paper
AkiomiUshida,TomiichiHasegawa,TakatsuneNarumi,ItaruKourakata,YoshinoriNakamoto, (2015) Flow Properties of Ultra-Fine Bubble Mixtures Passing through Micro-Apertures. Journal of Flow Control, Measurement & Visualization,03,111-121. doi: 10.4236/jfcmv.2015.33011
References
- 1. Sanders, W.C., Winkel, E.S., Dowling, D.R., Perlin, M. and Ceccio, S.L. (2006) Bubble Friction Drag Reduction in a High-Reynolds-Number Flat-Plate Turbulent Boundary Layer. Journal of Fluid Mechanics, 552, 353-380. http://dx.doi.org/10.1017/S0022112006008688
- 2. Shen, X., Ceccio, S.L. and Perlin, M. (2006) Influence of Bubble Size on Micro-Bubble Drag Reduction. Experiments in Fluids, 41, 415-424. http://dx.doi.org/10.1007/s00348-006-0169-y
- 3. Murai, Y., Fukuda, H., Oishi, Y., Kodama, Y. and Yamamoto, F. (2007) Skin Friction Reduction by Large Air Bubbles in a Horizontal Channel Flow. International Journal of Multiphase Flow, 38, 147-163.
http://dx.doi.org/10.1016/j.ijmultiphaseflow.2006.08.008 - 4. Mohanarangam, K., Cheung, S.C.P., Tu, J.Y. and Chen, L. (2009) Numerical Simulation of Micro-Bubble Drag Reduction Using Population Balance Model. Ocean Engineering, 36, 863-872.
http://dx.doi.org/10.1016/j.oceaneng.2009.05.001 - 5. Tom, G. and Liu, W. (2012) Measurement and Reduction of Micro-Bubble Formation in High-Viscosity Fluids. Proceedings of SPIE Advanced Lithography, Advances in Resist Materials and Processing Technology XXIX, 83252F, San Jose, 29 March 2012, 83252F. http://dx.doi.org/10.1117/12.927756
- 6. Nouri, N.M., Motlagh, S.Y., Navidbakhsh, M., Dalilhaghi, M. and Moltani, A.A. (2013) Bubble Effect on Pressure Drop Reduction in Upward Pipe Flow. Experimental Thermaland Fluid Science, 44, 592-598.
http://dx.doi.org/10.1016/j.expthermflusci.2012.08.022 - 7. Yanuar, Gunawan, Sunaryo and Jamaluddin, A. (2012) Micro-Bubble Drag Reduction on a High Speed Vessel Model. Journal of Marine Science and Application, 11, 301-304.
http://dx.doi.org/10.1007/s11804-012-1136-z - 8. Choi, Y.J., Park, J.Y., Kim, Y.J. and Nam, K. (2008) Flow Characteristics of Microbubble Suspensions in Porous Media as an Oxygen Carrier. Clean-Soil, Air, Water, 36, 59-65.
- 9. Jovanovic, J., Zhou, W., Rebrov, E.V., Nijhuis, T.A., Hessel, V. and Schouten, J.C. (2011) Liquid-Liquid Slug Flow: Hydrodynamics and Pressure Drop. Chemical Engineering Science, 66, 42-54.
http://dx.doi.org/10.1016/j.ces.2010.09.040 - 10. Miyamoto, M., Ueyama, S., Hinomoto, N., Saitoh, T., Maekawa, S. and Hirotsuji, J. (2007) Degreasing of Solid Surfaces by Microbubble Cleaning. Japanese Journal of Applied Physics, 46, 1236-1243.
http://dx.doi.org/10.1143/JJAP.46.1236 - 11. Liu, C., Tanaka, H., Zhang, L., Zhang, J., Huang, X., Ma, J. and Matsuzawa, Y. (2012) Fouling and Structural Changes of Shirasu Porous Glass (SPG) Membrane Used in Aerobic Wastewater Treatment Process for Microbubble Aeration. Journal of Membrane Science, 421-422, 225-231.
http://dx.doi.org/10.1016/j.memsci.2012.07.023 - 12. Versluis, M. (2012) Microbubble Acoustic Surface Cleaning. The Journal of the Acoustical Society of America, 131, 3337. http://dx.doi.org/10.1121/1.4708492
- 13. Lee, J.W., Kim, H.W., Sohn, J.I. and Yoon, G.S. (2013) A Study on Micro Bubbles Influence on Human Skin Cleaning. Advanced Science Letters, 19, 2558-2562. http://dx.doi.org/10.1166/asl.2013.4995
- 14. Ushida, A., Hasegawa, T., Amaki, K. and Narumi, T. (2013) Effect of Microbubble Mixtures on the Washing Rate of Surfactant Solutions in a Swirling Flow and an Alternating Flow. Tenside Surfactants Detergents, 50, 332-338. http://dx.doi.org/10.3139/113.110265
- 15. Burns, S.E., Yiacoumi, S. and Tsouris, C. (1997) Microbubble Generation for Environmental and Industrial Separations. Separation and Purification Technology, 11, 221-232.
http://dx.doi.org/10.1016/S1383-5866(97)00024-5 - 16. Fujiwara, A., Takagi, S., Watanabe, K. and Matsumoto, Y. (2003) Experimental Study on the New Micro-Bubble Generator and Its Application to Water Purification System. Proceedings of FEDSM2003, 4th Joint ASME/JSME Fluid Engineering Conference 2003, 2, 469-473.
http://dx.doi.org/10.1115/FEDSM2003-45162 - 17. Yamada, S., Yoshimi, Y., Terada, T., Ohno, K. and Minagawa, H. (2007) Study on Oxygen Supplying of the Micro- Bubbles Generated by the Pressurizing Dissolution Method. Japanese Journal of Multiphase Flow, 21, 84-90. (In Japanese) http://dx.doi.org/10.3811/jjmf.21.84
- 18. Tsuge, H., Li, P., Shimatani, N., Shimamura, Y., Nakata, H. and Ohira, M. (2009) Fundamental Study on Disinfection Effect of Microbubbles. Kagaku Kogaku Ronbunshu, 35, 548-552. (In Japanese)
http://dx.doi.org/10.1252/kakoronbunshu.35.548 - 19. Ohnari, H., Sato, K., Tonami, K., Watanabe, T., Nakagawa, Y., Chiba, S., Hata, T., Meyama, N., Yaguchi, J. and Ohnari, Y. (2012) Water Purification and Oyster Culture Reconstruction in Closed Sea Area Using Micro Bubble Technology. Japanese Journal of Multiphase Flow, 26, 150-157. (In Japanese)
http://dx.doi.org/10.3811/jjmf.26.150 - 20. Zhang, F., Xi, J., Huang, J.J. and Hu, H.Y. (2013) Effect of Inlet Ozone Concentration on the Performance of a Micro- Bubble Ozonation System for Inactivation of Bacillus Subtilis Spores. Separation and Purification Technology, 114, 126-133. http://dx.doi.org/10.1016/j.seppur.2013.04.034
- 21. Ikeura, H., Hamasaki, S. and Tamaki, M. (2013) Effect of Ozone Microbubble Treatment on Removal of Residual Pesticides and Quality of Persimmon Leaves. Food Chemistry, 138, 366-371.
http://dx.doi.org/10.1016/j.foodchem.2012.09.139 - 22. Ushida, A., Hasegawa, T., Kawami, M., Uchiyama, H., Narumi, T. and Kayaba, R. (2012) Flow Properties of Micro- Bubble/Polyethylene Glycol Mixtures Passing through Orifices and Slits. Nihon Reoroji Gakkaishi, 40, 61-68. http://dx.doi.org/10.1678/rheology.40.61
- 23. Hasegawa, T., Watanabe, H., Sato, T., Watanabe, T., Takahashi, M., Narumi, T. and Tiu, C. (2007) Anomalous Reduction in Thrust/Reaction of Water Jets Issuing from Microapertures. Physics of Fluids, 19, Article ID: 053102. http://dx.doi.org/10.1063/1.2723642
- 24. Ushida, A., Hasegawa, T., Kudou, S., Kawami, M., Uchiyama, H. and Narumi, T. (2011) Flow Properties of Several Types of Liquid Flows through Micro-Orifices. Journal of Fluid Science and Technology, 6, 802-811.
http://dx.doi.org/10.1299/jfst.6.802 - 25. Serizawa, A., Inui, T., Yahiro, T. and Kawara, Z. (2005). Pseudo-Laminarization of Micro-Bubble Containing Milky Bubbly Flow in a Pipe. Multiphase Science and Technology, 17, 79-101.
http://dx.doi.org/10.1615/MultScienTechn.v17.i1-2.50 - 26. Ushida, A., Hasegawa, T., Narumi, T., Amaki, K. and Kayaba, R. (2012) Drag Reduction Effect of Microbubble/Water Mixtures and Complex Fluids into Capillary Flows. Nihon Reoroji Gakkaishi, 40, 179-184. (In Japanese) http://dx.doi.org/10.1678/rheology.40.179
- 27. Davis, J.A., James, R.O. and Leckie, J.O. (1978) Surface Ionization and Complexation at the Oxide/Water Interface: I. Computation of Electrical Double Layer Properties in Simple Electrolytes. Journal of Colloid and Interface Science, 63, 480-499. http://dx.doi.org/10.1016/s0021-9797(78)80009-5
- 28. Takahashi, M., Chiba, K. and Li, P. (2007) Formation of Hydroxyl Radicals by Collapsing Ozone Microbubbles under Strongly Acidic Conditions. The Journal of Physical Chemistry B, 111, 11443-11446.
http://dx.doi.org/10.1021/jp074727m - 29. Choi, C.H., Ulmanella, U., Kim, J., Ho, C.M. and Kim, C.J. (2006) Effective Slip and Friction Reduction in Nanograted Superhydrophobic Microchannels. Physics of Fluids, 18, Article ID: 087105.
http://dx.doi.org/10.1063/1.2337669 - 30. Tandon, V. and Kirby, B.J. (2008) Zeta Potential and Electroosmotic Mobility in Microfluidic Devices Fabricated from Hydrophobic Polymers: 2. Slip and Interfacial Water Structure. Electrophoresis, 29, 1102-1114. http://dx.doi.org/10.1002/elps.200800735
- 31. Bohinc, K., Kralj-Iglic, V.K. and Iglic, A. (1993) Thickness of Electrical Double Layer, Effect of Ion Size. Electrochimica Acta, 46, 3033-3040. http://dx.doi.org/10.1016/S0013-4686(01)00525-4
- 32. Hasegawa, T., Asama, H. and Narumi, T. (2003) A Simple Method for Measuring Elastic Stresses by Jet Thrust and Some Characteristics of Tube Flows. Nihon Reoroji Gakkaishi, 31, 243-252.
http://dx.doi.org/10.1678/rheology.31.243
Nomenclatures
B: Width of slits (μm)
Db: Particle diameter of UFB (nm)
Dc: Capillary diameter (μm)
H: Thickness of slits (μm)
H/B: Thickness ratio (-)
K: Dimensionless pressure drop (-)
Lc: Capillary length between two pressure holes (mm)
Nb: Number density (mL−1)
p*: Dimensionless pressure component (-)
Q: Flow rate (m3s−1)
Re: Reynolds number (-)
SRapp: Apparent strainrate (s−1)
SRw: Shear rate on wall (s−1)
T: Temperature (˚C)
t*: Dimensionless time in numerical analysis (-)


V: Mean velocity passing through slits (ms−1)
Vc: Mean velocity passing through capillaries (ms−1)
W: Length of slits (μm)
x*: Dimensionless x direction in numerical region (-)
y*: Dimensionless y direction in numerical region (-)
Greek Letter
Δp: Pressure drop (Pa)
λ: Frictional coefficient of pipe (-)
μ: Viscosity (Pas)
ρ: Density (kgm−3)
τw: Wall shear stress (Pa)
















