Journal of Flow Control, Measurement & Visualization
Vol.03 No.02(2015), Article ID:55423,7 pages
10.4236/jfcmv.2015.32007
Hydrodynamic Performance Analysis of the Ducted Propeller Based on the Combination of Multi-Block Hybrid Mesh and Reynolds Stress Model
Xueming He1*, Hecai Zhao2, Xuedong Chen2, Zailei Luo2, Yannan Miao2
1Department of Electrical and Mechanical Management, China Maritime Police Academy, Ningbo, China
2State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan, China
Email: *hexueming66@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 October 2014; accepted 20 March 2015; published 8 April 2015
ABSTRACT
In order to analyze the hydrodynamic performance of the ducted propeller with high precision, this paper proposes a new method which combines Multi-Block Hybrid Mesh and Reynolds Stress Model (MBHM & RSM). The calculation errors of MBHM & RSM and standard two-equation model (standard k-ε model) on the ducted propeller JD7704 +Ka4-55 are compared. The maximum error of the total thrust coefficient KT, the duct thrust coefficient KTN, the torque coefficient KQ and the open-water efficiency η0 of MBHM & RSM are 2.98%, 4.01%, 1.46%, and 0.89%, respectively, which are lower than those of standard k-ε model. Indeed, the pressure distribution on the propeller surfaces, the pressure and the velocity vector distribution of the flow field are also analyzed, which are consistent with the theory. It is demonstrated that MBHM & RSM on the thruster dynamics analysis are feasible. This paper provides reference in the thruster designing of underwater robot.
Keywords:
Multi-Block Hybrid Mesh, RSM, Ducted Propeller, Hydrodynamic Performance

1. Introduction
The propeller of a Remotely Operated Vehicle (ROV) is an important part, whose dynamic performance determines the motion characteristics, control performance and efficiency of underwater robot. In recent years, many scholars engage in the research of the dynamics performance of the ducted propeller. For example, Baltazar et al. [1] analyzed the open water performance of the propeller with and without duct using panel method, but the error is high. Moustafa Abdel-Maksoud et al. [2] designed a multi-component propulsor, and the hydrodynamic performance is done in both 2D and 3D with numerical method. Long Yu et al. [3] investigated the open water performance of Ka-series propeller combined with 19A duct by the panel method and the numerical method, and a 3D-geometry generate method is proposed. H. Haimov et al. [4] combined the calculation methods and model tests to calculate the hydrodynamic problem of the Ka4-60-19A, and the RANSE solution has sufficient precision.
Yet, the finite element meshes in the numeral calculation of propeller mentioned above are regular grid, and the calculation models are limited to the two-equation model, such as the standard k-ε model, which may affect the precision and speed of calculation to some extent. Considering the complexity of the geometry, flow field characteristics and the precision of calculation, a kind of multi-block hybrid mesh combined with the RSM is put forward in this paper. The convection and diffusion effect of Reynolds stress is fully considered, and the Reynolds stress is directly solved with transport equation. Finally a good result is achieved.
2. Meshing and Boundary Conditions Set
Grid quality is one of the most important factors which affect the numerical precision and work efficiency in numerical calculation. Considering the complexity of the thruster structure and the advantages of structured and unstructured grids, multi-block hybrid meshing method is presented.
The ducted propeller is placed in a cylindrical flow field, as shown in Figure 1, the diameter of the column is 5D, the distance between the fluid entrance and front of the duct is 4D, the distance between the fluid outlet and back of the duct is 6D, the axis of the flow field coincides with the axis of the duct. The flow region of the thrust is divided into four parts. Unstructured meshes are used in the complex area adjacent to the propeller-area 1, and local crowded meshes are used near the propeller blade and hub position, and structured meshes are used in the area 2, area 3 and area 4; the grid density in area 2 is a little bigger than that in area 3 and area 4.
The grids on the surface of the propeller and the hub is generated with type of map and elements of quad, afterwards, the grids inside the duct is generated with type of TGrid and elements of Tet/Hybrid, which is shown in Figure 2. The mesh in area 2 area 3 and area 4 is generated with cooper and Hex/Wedge, which is shown in Figure 3.
Among them, TGrid and Tet/Hybrid means that the volume is divided mainly by tetrahedral cell, Hex/Wedge means that the mesh generated is hexahedral mesh, and some of them is wedge mesh, cooper means that the volume is divided according to the appointed source face.
The unstructured grid has good adaptability, reduced the difficulty in the mesh generation around the propeller, and the structured grid has good quality. The grid division method mentioned above not only reduces the grid number and improves the quality of mesh, but also improves the efficiency of the subsequent simulation.
In general, the flow region in the boundary is almost uniform mixture in numerical calculation. For the numerical calculation only need to obtain the time averaged data of the interaction between the propeller and the
Figure 1. Division of the computational domain.
Figure 2. Grid of the interior domain.
Figure 3. Grid of the exterior domain.
catheter, so the Moving Reference Frame (MRF) model is selected. And the flow field is divided into the internal catheter flow area and the external one, the interior area is defined as a rotation domain, the external one is defined as static domain. Inlet boundary is set as velocity inlet, the magnitude is constant and the direction is perpendicular to the entrance. Outlet boundary is set as pressure-outlet; the gauge pressure is given as 0. Interfaces between the rotation domain and the static domain are set as interface. The propeller and the duct are set as solid wall with no slip conditions. Considering that the RSM is effective under fully developed turbulent condition, and turbulence around the near wall region is not stable, the non-equilibrium wall function is adopted.
3. Selection of RSM Model and Open Water Performance of the Ducted Propeller
In order to use the experimental data of the JD7704 catheter +Ka4-55 propeller provided by Shanghai Jiao Tong University to verify the correct of our method and model, a matched propeller is designed. The structure is as shown in Figure 4 and its dimension in Table 1.
In the rotation of the propeller, the flow around the propeller is considered to be strong rotational flow, thus the turbulent flow is anisotropic. RSM considered the convection and diffusion of the Reynolds stress, and used the transport equation to solve the stress, avoided the viscosity hypothesis. RSM is a transport equation to solve the Reynolds stress tensor [5] , the equation is:
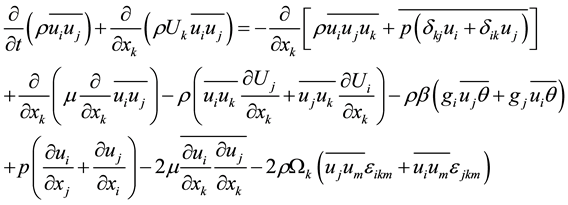 (1)
(1)
To simulate the effect of the wall to the distribution of Reynolds stress, the SSG model is chosen, which import the quadratic component of Reynolds stress anisotropic tensor to pressure and strain term. Thus the pressure and strain term is:
Figure 4. Geometry model of the ducted propeller.
Table 1. Geometry parameters of the propeller.
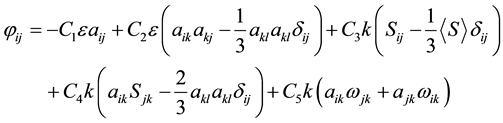 (2)
(2)
To study the mesh-dependency of the calculation, the open water performance of the ducted propeller under 200 thousands, 300 thousands, 500 thousands grids are calculated with RSM used. Through the simulation, the propeller thrust TP, duct thrust TN and the total torque Q under different advance coefficient is achieved, and the total thrust coefficient KT, the duct thrust coefficient KTN, the torque coefficient KQ and the open-water efficiency
η0 is calculated. Among them, the advance coefficient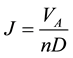 , the total thrust coefficient
, the total thrust coefficient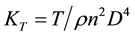 , the
, the
duct thrust coefficient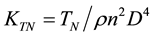 , the torque coefficient
, the torque coefficient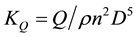 , the open-water efficiency
, the open-water efficiency
 . In the equation, ρ means the fluid density; T means the total force generated by the ducted propeller.
. In the equation, ρ means the fluid density; T means the total force generated by the ducted propeller.
The comparison of results under different grids is shown as Figure 5; we can see that the result with higher grid density is closer to the experimental result, but the results are stable in general. Considering the calculation efficiency and computational accuracy, the 300 thousands grid is chosen for later calculations.
In the calculation, the advance coefficient is defined from 0.1 to 0.8, the interval is 0.1. The simulation data and the error of the data are shown in Table 2. From the table, we can learn that the maximum error of torque coefficient KQ is 1.46%, the maximum error of duct thrust coefficient KTN is 4.01%, the maximum error of the total thrust coefficient KT is 2.98%, and the maximum error of the open water efficiency η0 is 0.89%. The conformity between numerical calculation and experimental data is very good, so we can conclude that the method proposed is feasible.
4. Pressure Nephogram Analyses on the Surface of the Blades of the Propeller
Thrust and torque of the propeller are the two macroscopic stresses. If we want to study the force of the propel-
Figure 5. Grid dependency of the calculation.
Table 2. The simulation data and the error.
ler in water meticulously, we need to carry out the force analysis in any arbitrary point on the propeller firstly. Figure 6 shows the pressure distribution in a propeller blade surface at the design point of J = 0.394.
From Figure 6, we can learn that: 1) on the pressure surface, the pressure decreases gradually from the leading edge to the trailing edge, whereas the pressure increases gradually from root to tip. Because of the mutual interference between the catheter and blade, the leading edge of the blade and the blade tip appears pressure drop; 2) on the bake surface, the suction decreases gradually from the leading edge to the trailing edge, and yet the suction increases gradually from root to tip, and reaches the maximum in the leaf tip. There are large differences between the catheter propeller blade and ordinary propeller in pressure distribution characteristics [6] [7] .
5. Working Flow Analysis of the Propeller
Figure 7 shows the pressure distribution of flow field of the ducted propeller. From the entrance of the flow to the blade surface of the propeller, the pressure value changes violently in the blade surface, and reaches to maximum, yet the pressure recovers on the back of the blade, and increases gradually from the back of the blade to the exit of the flow field. Thus, pressure difference exists in the blade of propeller to form thrust in the oppo-


Figure 6. Pressure distribution of the blade surface of the catheter propeller. (a) Pressure distribution of the blade surface; (b) Pressure distribution of the back surface of the blade.
Figure 7. The pressure distribution of the flow field.
site direction of the flow, which explains the working mechanism of ducted propeller.
Figure 8 shows the velocity vector of the ducted propeller at surface x = 0, we can see that the fluid velocity at both sides of the blade increases gradually from root to tip and a tip vortex forms at the blade tip.
6. Comparison of Computational Accuracy under Different Turbulent Models
At present, the two-equation models are also used to calculate swirling flow with high Reynolds number. To verify the advantage of RSM, the standard k-ε model is used to simulate the open water performance of the ducted propeller. The open water performance calculated by RSM and standard k-ε model is shown in Figure 9; we can see that RSM has better accuracy and RSM is more applicable to calculate the open water performance of the ducted propeller.
Figure 8. The velocity vector diagram.
Figure 9. Open water performance calculated by RSM and standard k-ε model.
7. Conclusions
This paper proposes a new method―the combination of the multi-block hybrid mesh and RSM, then it is used to analyze the flow field of ducted propeller, including the numerical calculation on the open water performance; finally, we draw conclusions:
1) Compared with the experimental data of JD7704 catheter +Ka4-55 propeller, the calculation results based on this method are in good agreement with experimental results in the thrust coefficient, torque coefficient and open water efficiency, so the method proposed in this paper is effective and feasible.
2) The flow field distribution characteristics of the ducted propeller are analyzed in this paper; the catheter can adjust the pressure distribution on the blade surface, which reduces the pressure difference in the blade tip, but cannot completely eliminate the tip vortex.
3) In the calculation of open water performance of ducted propeller, RSM has better accuracy than standard k-ε model; the method proposed provides reference for simulation of viscous flow around the complex rotating machine.
Acknowledgements
The work was supported by the Research Fund for the Doctoral Program of Chinese Higher Education (No. 20110142130010), and the Chinese Ministry of Public Security State Research Projects (No. 2011ZDYJHJXY 012).
References
- Baltazar, J., Falcão De Campos, J. and Bosschers, J. (2012) Open-Water Thrust and Torque Predictions of a Ducted Propeller System with a Panel Method. International Journal of Rotating Machinery, Article ID: 474785. http://dx.doi.org/10.1155/2012/474785
- Abdel-Maksoud, M., Steden, M. and Hundemer, J. (2010) Design of a Multi-Component Propulsor. Proceedings of 28th Symposium on Naval Hydrodynamics, Pasadena, 12-17 September 2010, 744-758.
- Yu, L., et al. (2013) Numerical Analysis of Ducted Propeller Performance under Open Water Test Condition. Journal of Marine Science and Technology, 18, 381-394. http://dx.doi.org/10.1007/s00773-013-0215-4
- Haimov, H., et al. (2010) Ducted Propellers. A Solution for Better Propulsion of Ships Calculations and Practice. Proceedings of 1st International Symposium on Fishing Vessel Energy Efficiency E-Fishing, Vigo, 265-271.
- Peng, H.H., Qiu, W. and Ni, S. (2013) Effect of Turbulence Models on RANS Computation of Propeller Vortex Flow. Ocean Engineering, 72, 304-317. http://dx.doi.org/10.1016/j.oceaneng.2013.07.009
- Pan, X., Zhang, J.-Y. and Liu, C.-J. (2011) Numerical Simulation and Analysis of Cavitation Characteristics of Ship Propeller. Intelligence Information Processing and Trusted Computing (IPTC), Wuhan, 22-23 October 2011, 180-183. http://dx.doi.org/10.1109/IPTC.2011.53
- Choong, W.H., et al. (2013) Outboard Marine Propeller Performance Analysis through CFD Modelling. Computer Modelling and Simulation (UKSim), Cambridge, 10-12 April 2013, 310-323.
NOTES
*Corresponding author.















