Journal of Flow Control, Measurement & Visualization
Vol.2 No.1(2014), Article ID:42324,6 pages DOI:10.4236/jfcmv.2014.21003
Effect of Thermal Convection on Viscosity Measurement in Vibrational Viscometer
1Department of Mechano-Micro Engineering, Tokyo Institute of Technology, Tokyo, Japan
2Precision and Intelligence Laboratory, Tokyo Institute of Technology, Tokyo, Japan
3Graduate School of Science and Technology, Niigata University, Niigata, Japan
4Visualization Research Center, Niigata University, Niigata, Japan
Email: aliakpek@gmail.com
Copyright © 2014 Ali Akpek et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Ali Akpek et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 14, 2013; revised November 28, 2013; accepted November 30, 2013
KEYWORDS
Viscosity Measurement; Vibrational Viscometer; Thermal Convection; Rayleigh Number; PIV
ABSTRACT
This paper describes the experimental study of viscosity measurement error in the vibrational type viscometer, which measures viscous damping of the oscillating circular plate in a fluid in continuously increasing temperatures. The experiments are carried out to measure non-uniformity of the temperature field in the test cup of the vibrational viscometer in continuously increasing temperatures, while changing the viscosity of the target fluids. Experimental outcomes show that non-uniformity of the temperature grows in the cup and results in viscosity measurement error, when the viscosity of the fluid increases. In order to understand this phenomenon, velocity measurement by particle image velocimetry is conducted in the test cup for fluids of varying viscosity. The results indicate that mixing is enhanced in the low-viscosity fluid by the occurrence of unsteady thermal convection, while weaker convection appears in the high-viscosity fluid.
1. Introduction
The vibrational type viscometer is a newly developed viscometer featuring efficacious continuous viscosity measurement capability, low cost and ease of use in comparison with other types of viscometer [1-7]. The basic principle of the vibrational viscometer is that viscous damping of the oscillation amplitude of a circular plate in the target fluid is proportional to the product of the fluid viscosity and density, which are functions of the temperature of the fluid. Therefore, accuracy of the temperature measurement is very important for highly accurate measurement of the viscosity of the fluid. However, there are few studies on viscosity error due to non-uniformity of the temperature field in the fluid [8].
The viscosity measurement in the vibrational viscometer requires knowledge of the thermal convection in a test cup, which is heated from the bottom and the sides of the rectangular cup. Normally, heating from the bottom and sides of the cup causes thermal convection, which promotes mixing of the fluid inside, and results in a uniform temperature field [9-13]. Therefore, the magnitude of the thermal convection is a key to understanding the temperature fields in the cup and the accuracy of the viscosity measurement in the vibrational viscometer.
The purpose of this paper is to study the non-uniform temperature field of the vibrational viscometer for various viscosities of fluids by measuring the temperature distributions and velocity field in the test cup.
2. Experiments
2.1. Experimental Apparatus
Figure 1 shows a schematic illustration of the vibrational viscometer, which is composed of electromagnetic driving unit, oscillators, thermometry, test cup, heating water unit and heater. Normally, the diameter of the oscillator is 10 mm and it oscillates at a frequency of 30 Hz with

Figure 1. Front view of vibrational viscometer.
amplitude of 0.4 mm, while the volume of the test cup is large enough having a height of 40 mm and horizontal dimensions of 64 mm × 24 mm. For this reason, the present experiment is designed to measure the non-uniform temperature field in the test cup without the oscillator unit. It should be mentioned that the volume of the heating cup is 3375 cm3, which is large enough in comparison with that of the test cup (61.4 cm3). The test cup is made of acrylic resin material, 2 mm thick. The test fluid was supplied to the test cup up to 30 mm in height. The height of the free surface of the test fluid is made equal to that of the heating cup, which is filled with water for heating the test cup. The water in the heating cup is heated from below using the heater unit. The characteristics of the test fluids that are used during the experiments are listed in Figure 2. The test fluids are silicon oils from Shin-etsu Chemical Co. They are referred to as fluid A (KF-96-100 cS), fluid B (KF-96-1000 cS) and fluid C (KF-96H-10,000 cS), which show different kinematic viscosity ν = 100, 1000 and 10,000 mm2/s, respectively at 25 deg C, while having the same specific heat 1.5 J/gK and the same thermal conductivity 0.16 W/mK.
2.2. Temperature Measurement
For continuous temperature measurements in the test cup, three thermometers are placed in different parts of the test cup, which is immersed into a heating cup. The thermometers are positioned in the center and near-wall of the test cup along the long axis of the test cup. Temperature measurement experiments for selected fluids are repeated three times and the average values are used to form a non-uniform temperature field for the fluids. During the experiments, the heating water was heated from below by the heater unit. The temperature readouts of all thermometers were recorded simultaneously.
2.3. Flow Visualization
In order to understand the physical phenomenon in the
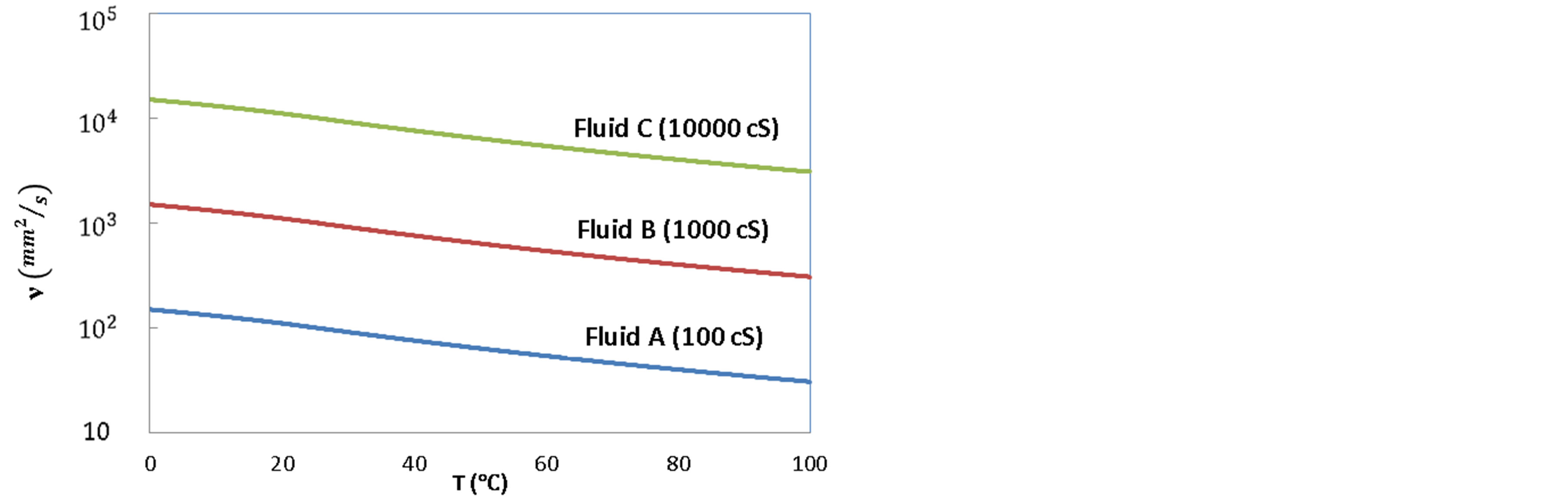
Figure 2. Variations of fluid viscosity with temperature.
test cup, the velocity field was measured by particle image velocimetry (PIV). The experimental set-up for flow visualization is illustrated in Figure 3. Flow visualization in the test cup was achieved by introducing a small amount of nylon tracer particles into the test fluid. The diameter of the tracers for flow visualization is 20 μm and the specific gravity is 1.02. The planar measurement of the velocity field in the test cup was carried out using the PIV system, which consists of a CW Nd:YAG laser of 8 W power and a high-speed CMOS camera (1280 × 1024 pixels with 8 bit), which is operated by a pulse controller. The CMOS camera is located 550 mm from the test vessel. The frame rate of the camera was set to 130 frames/sec and the exposure time was 7.6 msec. Note that the focal length of the camera lens was 75 mm with f-number 2.8 and the thickness of the light sheet was about 1 mm.
The target plane of measurement is vertical planes through the center of the cup normal to each other to observe the three-dimensional cell structure in the test cup. The vertical light sheet was projected from the laser source for the illumination. Measurement of the velocity field was carried out for the time period of 5 sec. every 0.1 sec. Therefore, 50 sequential images are taken in the measurement and the instantaneous velocity fields are evaluated from the successive two images with certain time interval and they are short-time-averaged for the period of 5 sec. to remove invalid velocity vectors, which are random in space and time.
The PIV analysis between the successive two images is carried out using the direct cross-correlation algorithm with the sub-pixel interpolation technique [14,15]. The interrogation window size is set to 31 × 31 pixels and the candidate region is searched in an area of 51 × 51 pixels to minimize the invalid velocity vectors, while keeping a reasonable spatial resolution.
3. Results and Discussions
3.1. Temperature Measurements
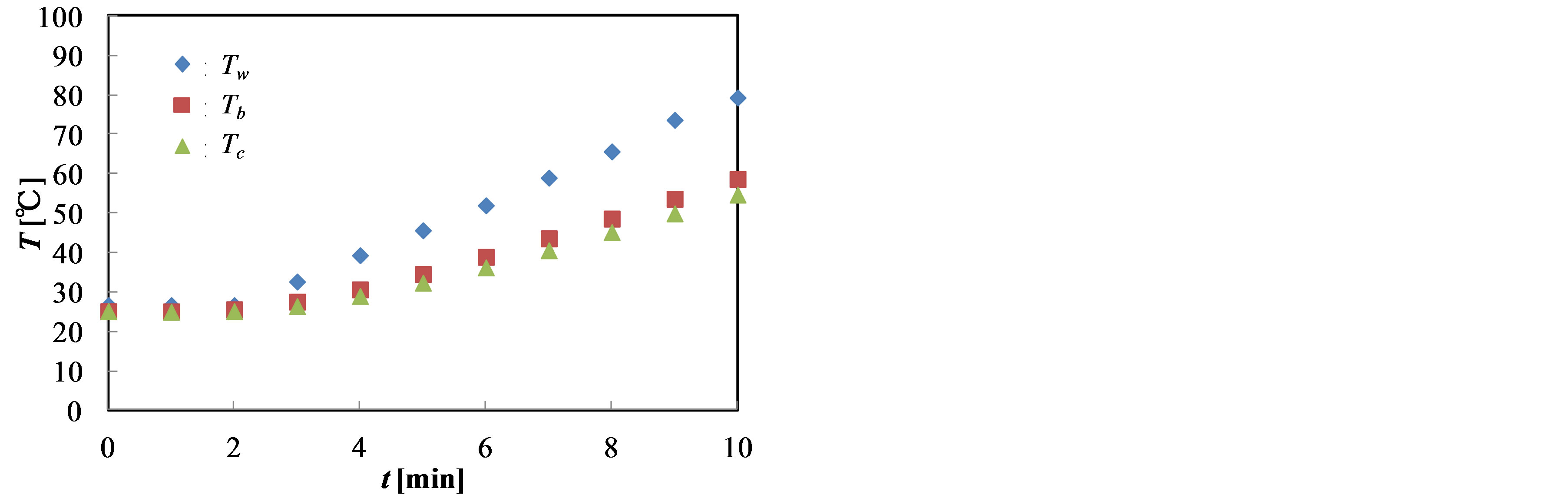
Figure 4 shows the time-variation of temperatures of test

Figure 3. Experimental set-up for flow visualization.
 (a)
(a)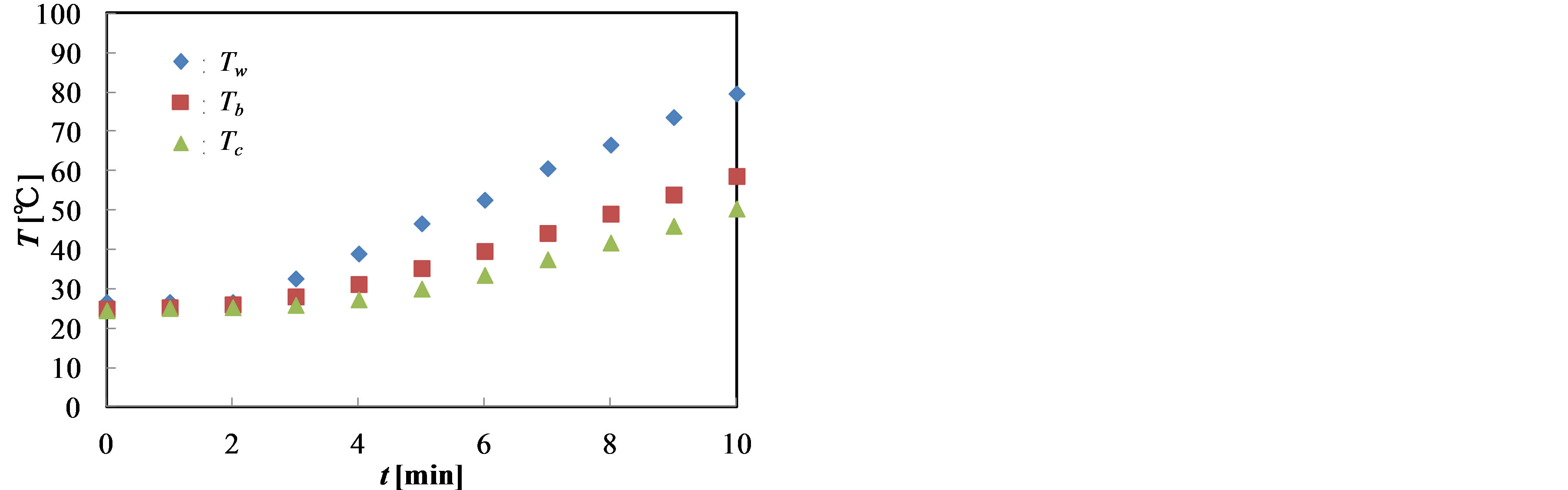 (b)
(b) (c)
(c)
Figure 4. Time-variation of non-uniform temperature field in test cup. (a) Fluid A (100 cS); (b) Fluid B (1000 cS); (c) Fluid C (10,000 cS).
fluids in the test cup and that of the heating water, which are measured by the thermocouples. The temperature in the center of the cup is denoted by Tc and that near the sidewall is Tb, while the temperature in the heating water is Tw. All the temperatures increase gradually with increasing time t after the heating starts. Note that the temperatures of the test fluid and the heating water are kept at the same temperature at the start of heating. Although the relationship between the temperature in the heating water and time is not influenced by the fluid viscosities, the temperatures Tc and Tb in the cup do change with the viscosities of the fluid and the temperature difference increases especially for the high-viscosity fluid. It is interesting to see that Tb is closer to Tc for the lowviscosity fluid, while it stays in the mid of Tw and Tc for the high-viscosity fluid. This may indicate higher mixing of the low-viscosity fluid in the cup. This result indicates that the temperature error in the test cup is influenced by the viscosity of the target fluid.
3.2. Variations of Rayleigh Numbers
In order to understand the thermal convection phenomenon in the test cup, the Rayleigh number Ra is evaluated for the three fluids, which are shown in Figure 5. The Rayleigh number is defined by , where d is the height of the fluid,
, where d is the height of the fluid,  the temperature difference between the heating water and the center of the test fluid, g the gravitational acceleration, α the volume expansion coefficient, ν the kinematic viscosity and κ the thermal diffusivity. The time variations of the Rayleigh number for test fluids shows that the Rayleigh number increases rapidly in the initial stage of heating and it tends to be saturated in the later stage of heating. It should be mentioned that the Rayleigh number is around 106 for test fluid A, 105 for test fluid B and 104 for test fluid C in the later stage. This difference in the Rayleigh number is mainly due to the influence of test fluid viscosity. According to the previous study, the critical Rayleigh number for the onset of laminar convection is
the temperature difference between the heating water and the center of the test fluid, g the gravitational acceleration, α the volume expansion coefficient, ν the kinematic viscosity and κ the thermal diffusivity. The time variations of the Rayleigh number for test fluids shows that the Rayleigh number increases rapidly in the initial stage of heating and it tends to be saturated in the later stage of heating. It should be mentioned that the Rayleigh number is around 106 for test fluid A, 105 for test fluid B and 104 for test fluid C in the later stage. This difference in the Rayleigh number is mainly due to the influence of test fluid viscosity. According to the previous study, the critical Rayleigh number for the onset of laminar convection is

Figure 5. Time-variation of Rayleigh number in measurements.
known to be 1700 for the horizontal fluid layer heated from below [10], and the transition to turbulent state is observed around 105 [16]. In reference to these results, the flow in the test cup is in the turbulent state of thermal convection for the fluids A and B, while that for fluid C is in the laminar state of thermal convection.
3.3. Visualization of Flow Patterns
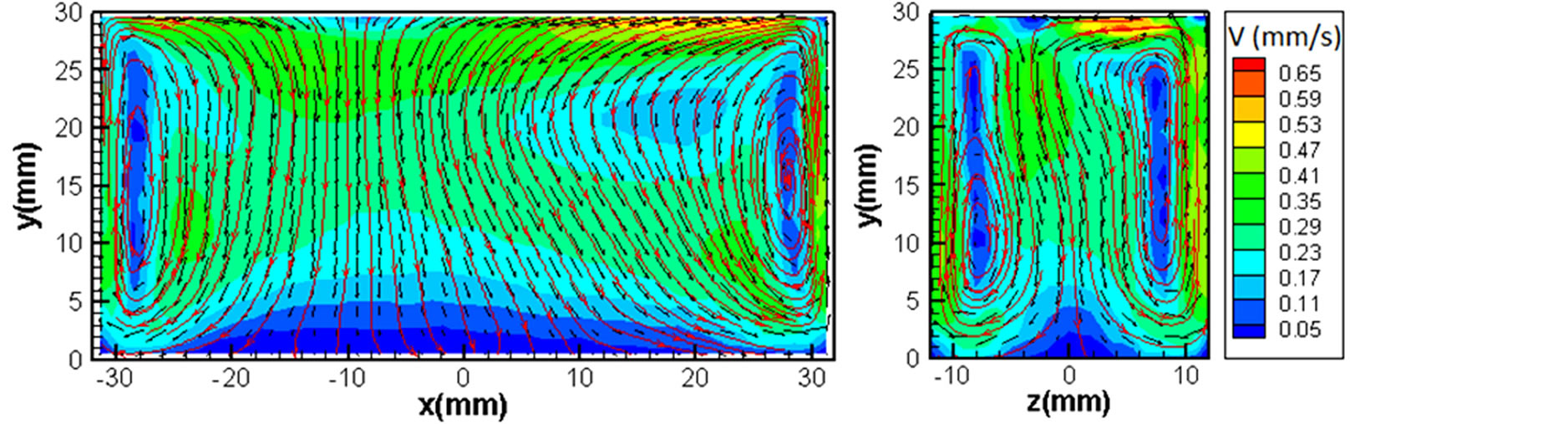
Figures 6(a) and (b) shows measurements of the velocity fields in the planar sections viewed from the front and the side of the test cup through the center of the fluid A at heating times of 4 min. and 8 min., respectively, which are obtained from the present PIV experiment. These figures show the velocity vectors, velocity magnitude and streamlines, to understand the flow field inside the test cup. Note that the velocity magnitude v is shown by color bars. These results indicate that there exists a thermal convection pattern inside the test cup. The flow pattern inside the test cup is driven by the heating on the side walls, so that the vertical upward flow appears along the side walls and the downward flow is generated in the center of the test cup toward the bottom wall; then the flow spreads back to the side walls again. Such thermal convection pattern in the test cup is clearly seen in the observation from the side due to the two-dimensional characteristics of the cell structure. It should be mentioned that the cell pattern is asymmetric with respect to the center plane, because the Rayleigh number 2.5 × 105 is large enough for the flow to be unsteady. With an increase in heating time to t = 8 min, the velocity magnitude in the convection pattern in the test cup increases and the flow pattern becomes more asymmetrical and unsteady, which is reflected by the growth of Rayleigh number to 6.6 × 105.
Figures 7 and 8 show the velocity fields in the test cup for fluids B and C, respectively, at 8 min from the start of heating. These results indicate that the magnitude of the thermal convection decreases with an increase in the viscosity of the fluid, which corresponds to a decrease in Rayleigh number. Therefore, the influence of thermal convection becomes weaker for the highly viscous fluids. This result meets well with the experimental observation of temperature variations in the test cup and the Rayleigh number variation in Figure 5. It is also found from these results that the cell pattern in the test cup becomes symmetrical with respect to the central plane of the test cup for higher-viscosity fluids, which is due to the decrease in Rayleigh number of the fluids. This indicates that the thermal convection becomes weaker and the temperature difference in the test cup becomes large in the high-viscosity fluid, so that the error of viscosity measurement will be increased. Therefore, it is recommended to increase forced convection in the test cup, in order to increase the accuracy of viscosity measurement in highviscosity fluids.
4. Conclusion
This study focused on the topic of non-uniform tempera-
 (a)
(a)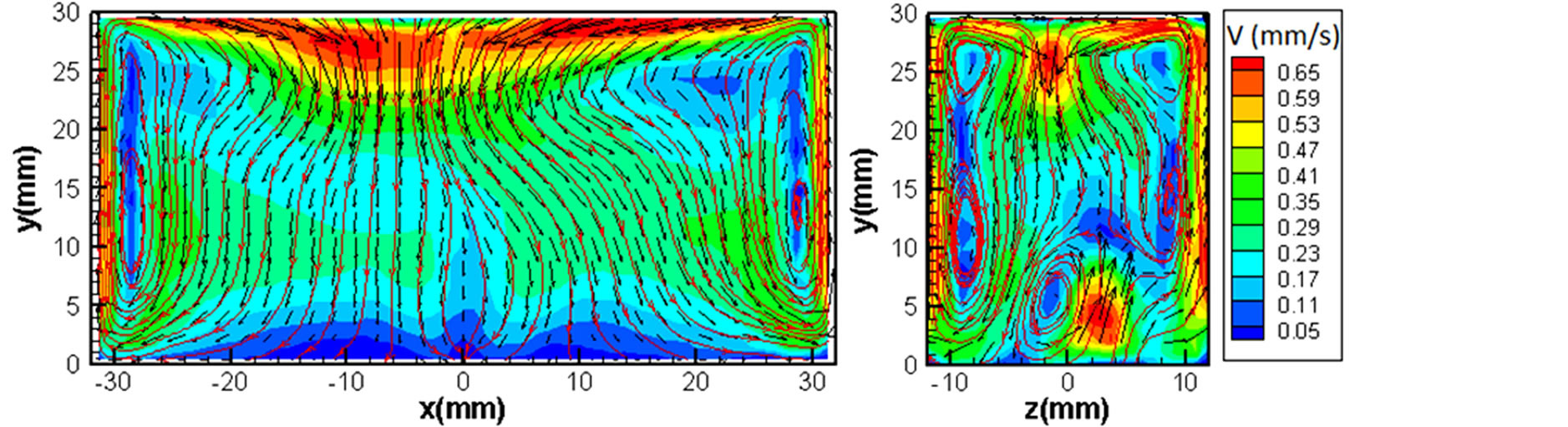 (b)
(b)
Figure 6. Velocity field in test cup for fluid A (100 cS). (a) t = 4 min; (b) t = 8 min.
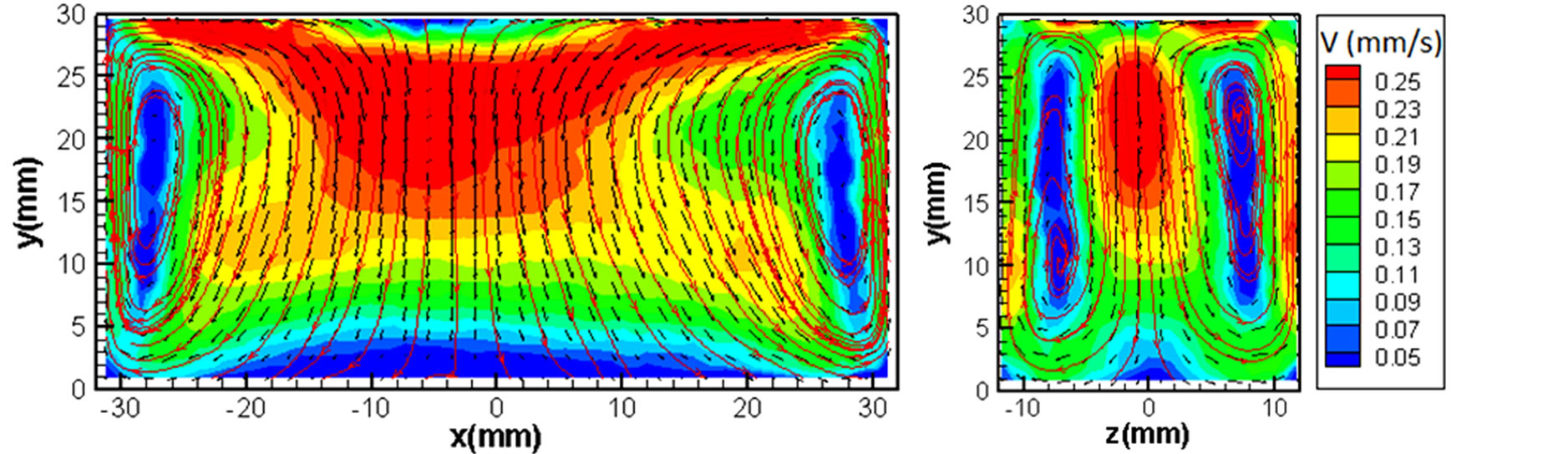
Figure 7. Velocity field in test cup for fluid B (1000 cS) (t = 8 min).

Figure 8. Velocity field in test cup for fluid C (10,000 cS) (t = 8 min).
ture distribution in vibrational viscometers. In order to understand the mechanism, the measurement of nonuniform temperature distribution in the test cup was carried out for three fluids of different viscosity. The results indicate that the non-uniform temperature appears strongly in high viscosity fluids due to weakened thermal convection inside the test cup. The PIV measurement in the test cup shows that mixing is enhanced by the unsteady thermal convection for the low-viscosity fluid, while the magnitude of convection is weakened in the high-viscosity fluid. These results indicate the importance of thermal mixing in the test cup to increase the accuracy of viscosity measurement by the vibrational viscometer.
Acknowledgements
The authors would like to thank the international standard committee of SICE and A&D Company.
REFERENCES
- S. H. Maron, I. M. Krieger and A. W. Sisko, “A Capillary Viscometer with Continuously Varying Pressure Head,” Journal of Applied Physics, Vol. 25, No. 8, 1954, pp. 971-976. http://dx.doi.org/10.1063/1.1721811
- J. Kestin and G. F. Newell, “Theory of Oscillation Type Viscometers: The Oscillating Cup,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 8, No. 6, 1957, pp. 433-449. http://dx.doi.org/10.1007/BF01600560
- P. J. Gilinson Jr., C. R. Dauwalter and E. W. Merrill, “A Rotational Viscometer Using an A.C. Torque to Balance Loop and Air Bearing,” Journal of Rheology, Vol. 7, 1963, pp. 319-331. http://dx.doi.org/10.1122/1.548960
- M. M. Abu-Orf, C. A. Walker and S. K. Dentel, “Centrate Viscosity for Continuous Monitoring of Polymer Feed in Dewatering Applications,” Advances In Environmental Research, Vol. 7, No. 3, 2003, pp. 687-694. http://dx.doi.org/10.1016/S1093-0191(02)00036-9
- A. Fedorchenko, I. Satchiv and A.-B. Wang, “The Optical Viscometer Based on the Vibrating Fiber Partially Submerged in Fluid,” Sensors and Actuators B, Vol. 142, No. 1, 2009, pp. 111-117. http://dx.doi.org/10.1016/j.snb.2009.07.028
- N. Izumo and A. Kowai, “Technological Background and Latest Market Requirements Concerning ‘Static Viscosity’ Measurement with a Tuning-fork Vibration Viscometer,” Proceedings of Asia-Pacific Symposium on Measurement of Mass, Force and Torque, Tokyo, 1-4 June 2009, pp. 51-57.
- A. Fedorchenko, I. Satchiv and W.-C. Wang, “Method of the Viscosity Measurement by Means of the Vibrating Micro-Nano-Mechanical Resonators,” Flow Measurement and Instrumentation, Vol. 32, 2013, pp. 84-89. http://dx.doi.org/10.1016/j.flowmeasinst.2013.03.003
- ASTM D2162-13, “Standard Practice for Basic Calibration of Master Viscometers and Viscosity Oil Standards,” ASTM, 2013.
- R. J. Adrian, R. T. D. S. Ferreira and T. Boberg, “Turbulent Thermal Convection in Wide Horizontal Fluid Layer,” Experiments in Fluids, Vol. 4, No. 3, 1986, pp. 121-141.
- E. L. Koschmieder, “Bernard Cells and Taylor Vortices,” Cambridge University Press, Cambridge, 1993, pp. 1-195.
- N. Fujisawa and R. J. Adrian, “Three-dimensional Temperature Measurement in Turbulent Thermal Convection by Extended Range Scanning Liquid Crystal Thermometry,” Journal of Visualization, Vol. 1, No. 4, 1999, pp. 355-364. http://dx.doi.org/10.1007/BF03181425
- N. Fujisawa, S. Funatani and N. Katoh, “Scanning Liquid-Crystal Thermometry and Stereo Velocimetry for Simultaneous Three-Dimensional Measurement of Temperature and Velocity Field in a Turbulent RayleighBernard Convection,” Experiments in Fluids, Vol. 38, No. 3, 2005, pp. 291-303. http://dx.doi.org/10.1007/s00348-004-0891-2
- F. Corvaro and M. Paroncini, “An Experimental Study of Natural Convection in a Differentially Heated Cavity through a 2D-PIV System,” International Journal of Heat and Mass Transfer, Vol. 52, No. 1-2, 2009, pp.355-365. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.05.039
- M. Kiuchi, N. Fujisawa and S. Tomimatsu, “Performance of PIV System for Combusting Flow and Its Application to Spray Combustor Model,” Journal of Visualization, Vol. 8, No. 3, 2005, pp. 269-276. http://dx.doi.org/10.1007/BF03181505
- M. Raffel, C. Willert and J. Kompenhans, “Particle Image Velocimetry, Practical Guide,” Springer, Berlin, 1998, pp. 1-146. http://dx.doi.org/10.1007/978-3-662-03637-2_1
- B. Castaing, G. Gunaratne, F. Heslot, L. Kadanoff, A. Libchaber, S. Thomae, X.-Z. Wu, S. Zaleski and G. Zanetti, “Scaling of Hard Thermal Turbulence in RayleighBernard Convection,” Journal of Fluid Mechanics, Vol. 204, 1989, pp. 1-30. http://dx.doi.org/10.1017/S0022112089001643
Nomenclature
d: depth of fluid g: gravitational acceleration Ra: Rayleigh number (=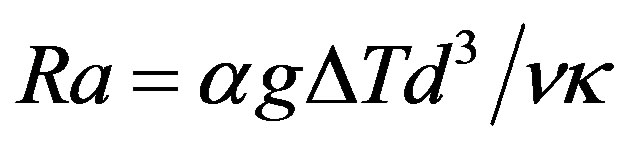 )
)
T: temperature t: time Tb: temperature near sidewall Tc: temperature at center Tw: temperature of heating water v: velocity magnitude x, y, z: coordinates
α: volume expansion coefficient
ν: kinematic viscosity
κ: thermal diffusivity

