Journal of Flow Control, Measurement & Visualization
Vol.1 No.3(2013), Article ID:37598,8 pages DOI:10.4236/jfcmv.2013.13012
Stability of Subsonic Jet Flows*
Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch of Russian Academy of Sciences, Novosibirsk, Russia
Email: kozlov@itam.nsc.ru
Copyright © 2013 Victor V. Kozlov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 10, 2013; revised July 12, 2013; accepted July 23, 2013
Keywords: Subsonic Jets; Hydrodynamic Instability; Transition to Turbulence; Flow Visualization
ABSTRACT
An overview of recent experimental results on instability and dynamics of jets at low Reynolds numbers is given. Round and plane, macro and micro jets are under the consideration. Basic features of their evolution affected by initial conditions at the nuzzle outlet and environmental perturbations are demonstrated.
1. Introduction
Stability of jet flows has been extensively studied both theoretically and experimentally. Some key results on stability characteristics and development of coherent structures of round and plane jets are presented in Refs. [1-6], respectively. The behavior of a round jet in a cross flow is investigated in detail in Refs. [7-9]. Last years, the amount of publications on micro jet flows and external effects on their evolution rapidly grows, see, e.g., Refs. [10-12]. An overview of the current state of the problem is given in our recent monograph [13] which is primarily based on the original research data of Refs. [14-22].
In the present paper which is structured similar to Ref. [13] we summarize briefly our main observations of instability phenomena in different conditions of the jet origination and evolution. The experimental results reported in the following sections were obtained in several air jet facilities at low subsonic velocities. Both naturally occurring and artificially generated flow disturbances were investigated. Details on the dominant flow perturbations and their interactions became available at visualization. Quantitatively the flow characteristics were examined through hot-wire measurements.
2. Evolution and Breakdown of Laminar Round Jets
The focus of this section is the origination and evolution of longitudinal structures (or streaky structures) of laminar flow disturbances in a round jet. Of special interest is their interaction with the Kelvin-Helmholtz vortices stimulating the laminar flow breakdown and enhancing mixing of the jet with ambient air. The original experimental results on this subject are reported in Refs. [14,15].
2.1. Round Jet Visualization
The round jet with the so-called “top-hat” initial mean velocity profile is visualized in its different sections by smoke as is shown in Figure 1. In this case, the longitudinal structures of stationary flow perturbations emerging naturally at the jet periphery are observed close to the nozzle outlet. The longitudinal structures become more pronounced at their controlled generation by roughness elements periodically spaced at the nozzle surface, see Figure 2. At the nozzle outlet the jet boundary is nearly sinusoidal along the full circumference (Figure 2(b)). While moving downstream, mushroom-like structures are generated in the jet shear layer due to interaction of the longitudinal disturbances with the ring vortices (Figures 2(c)-(g)). The periodic flow pattern is obviously destroyed in the last section (Figure 2(h)). Spatial arrangement of the dominant perturbations of the jet is further illustrated in Figure 3.
2.2. Vortex Model
Laminar jet breakdown at the interaction of the longitudinal structures with the ring vortices resembles the nonlinear deformation of two-dimensional waves by local flow non-uniformities in boundary layers where the Λ-shaped structures are generated appearing as two vortices rotating in opposite directions with a “head” at their tips. In the present case, such non-uniformities are the longitudinal
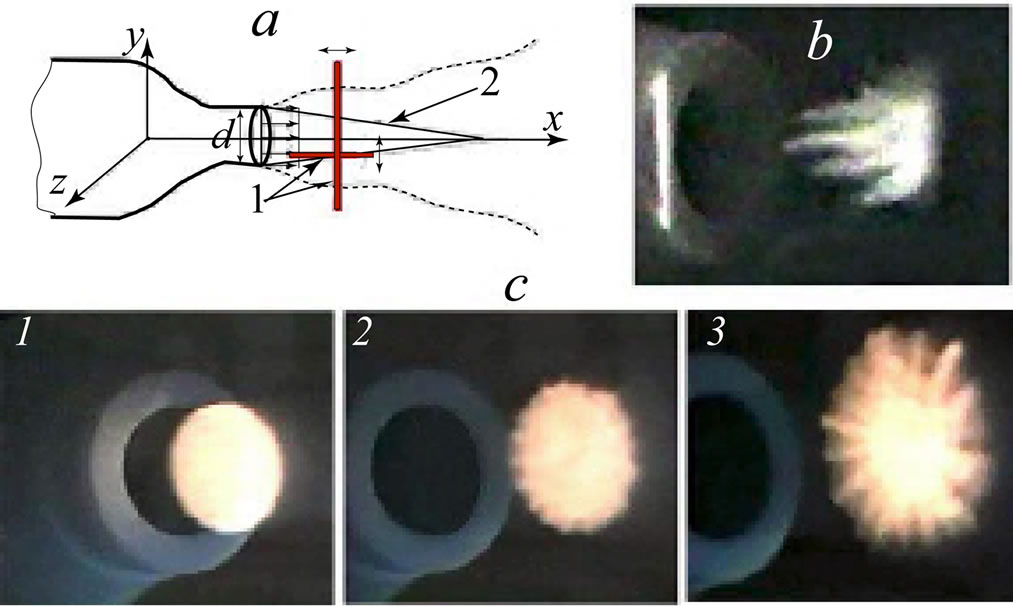
Figure 1. Natural streaky structures in the near field of the round jet (nozzle diameter d = 40 mm, jet core velocity U0 = 4 m/s, Red = 10,600): experimental scheme (potential jet core is illuminated by thin light sheets, marked by 1 and 2) (a); smoke visualization of the streaky structures in the streamwise section z/d = 0.4 (b); cross sections at x/d = 0.4 (1), 0.68 (2), 0.86 (3) (c).
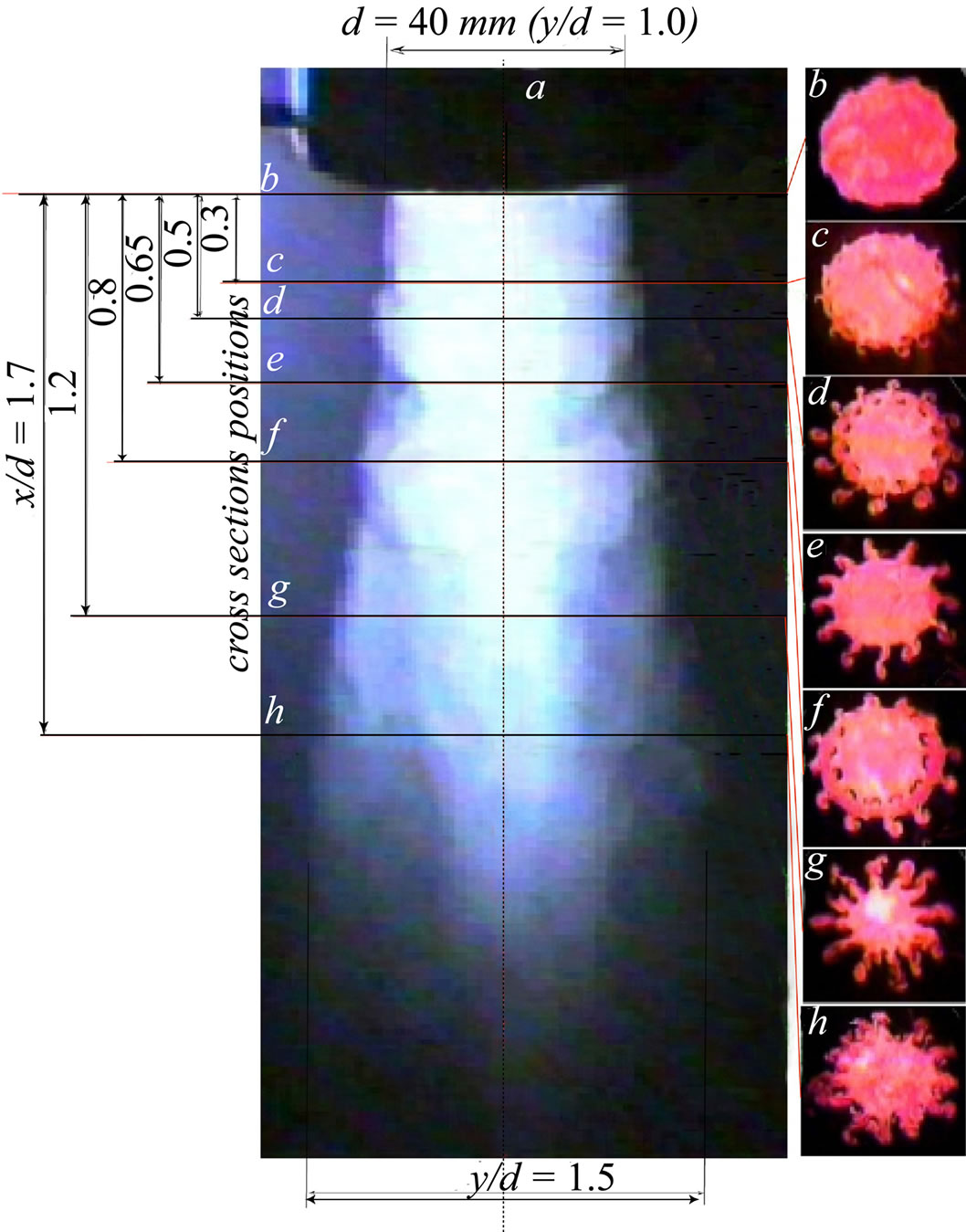
Figure 2. General view of the round jet (a) and its cross sections at different distance from the nozzle exit (b)-(h).
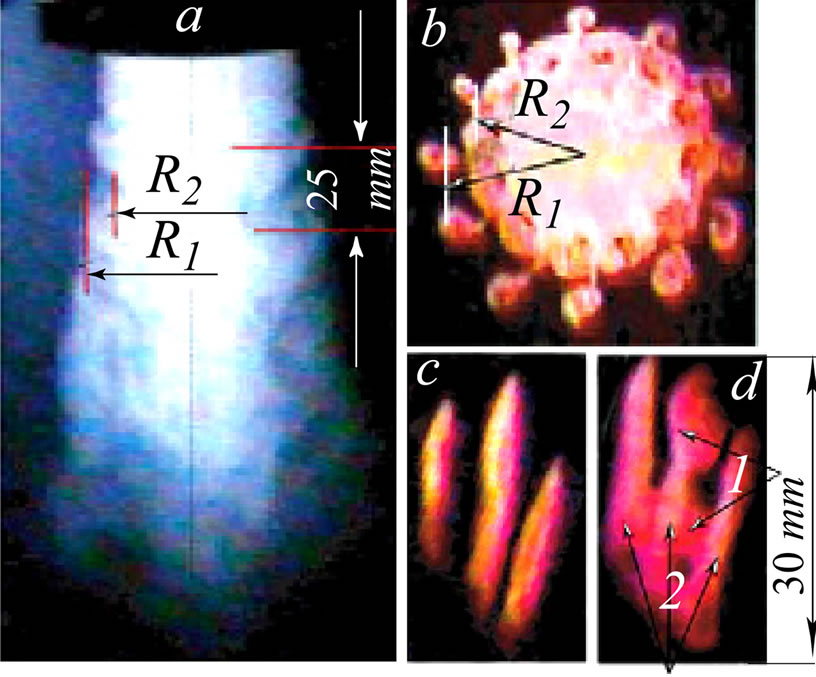
Figure 3. General view of the round jet (а); a cross section (b); streamwise sections at R1 (c) and R2 (d); positions of the ring vortices and the longitudinal perturbations are marked by 1 and 2, respectively.
perturbations as is sketched in Figure 4. A two-dimensional ring vortex, while passing through the flow region perturbed by the longitudinal disturbances, interacts with them and undergoes a three-dimensional deformation which results in the characteristic bursts well seen all over the jet periphery. Those observed in Figure 2 look similar to the “heads” of Λ-structures in a boundary layer.
3. Instability of Free and Wall Plane Jets
We proceed with plane jets focusing, again, the formation and development of longitudinal structures of laminar flow disturbances [16].
3.1. Perturbations of the Free Plane Jet
A sequence of the jet cross sections is given in Figure 5. The visualization data demonstrate a result of the interaction between the longitudinal disturbances induced by controlled roughness elements at the nozzle surface and the Kelvin-Helmholtz vortices, i.e., the development of periodic mushroom—like structures spreading from the shear layer into surrounding fluid.
3.2. Perturbations of the Wall Plane Jet
The wall jet is distinguished by two characteristic layers, that is, the inner one which is similar to a near-wall boundary layer and the external free shear layer being far from the surface. The corresponding mean velocity profiles are shown in Figure 6.
Visualization of natural perturbations of the wall jet is presented in Figure 7. The longitudinal structures are well seen together with the Kelvin-Helmholtz vortices in the x-z plane at the light sheet parallel to the wall (Figure 7(a)). Also, the three-dimensional disturbances are visible in the y-z plane at the light sheet perpendicular to the surface (Figure 7(b)). Most likely, their origination is due to local flow perturbations arising in the settling chamber of the jet facility.
3.3. Forced Longitudinal Structures of the Wall Plane Jet
More details about the disturbed flow pattern are available through hot-wire measurements of the controlled perturbations. In the present case, they are generated in the free shear layer of the jet by roughness elements at the nozzle outlet and are examined through hot-wire measurements performed with a high spatio-temporal resolution. The results are shown in Figure 8 as deviations of mean velocity from its value averaged over the transverse coordinate. As is found, the controlled disturbances of the free shear layer induce similar perturbations in the boundary layer, however, differing by their transverse scales.
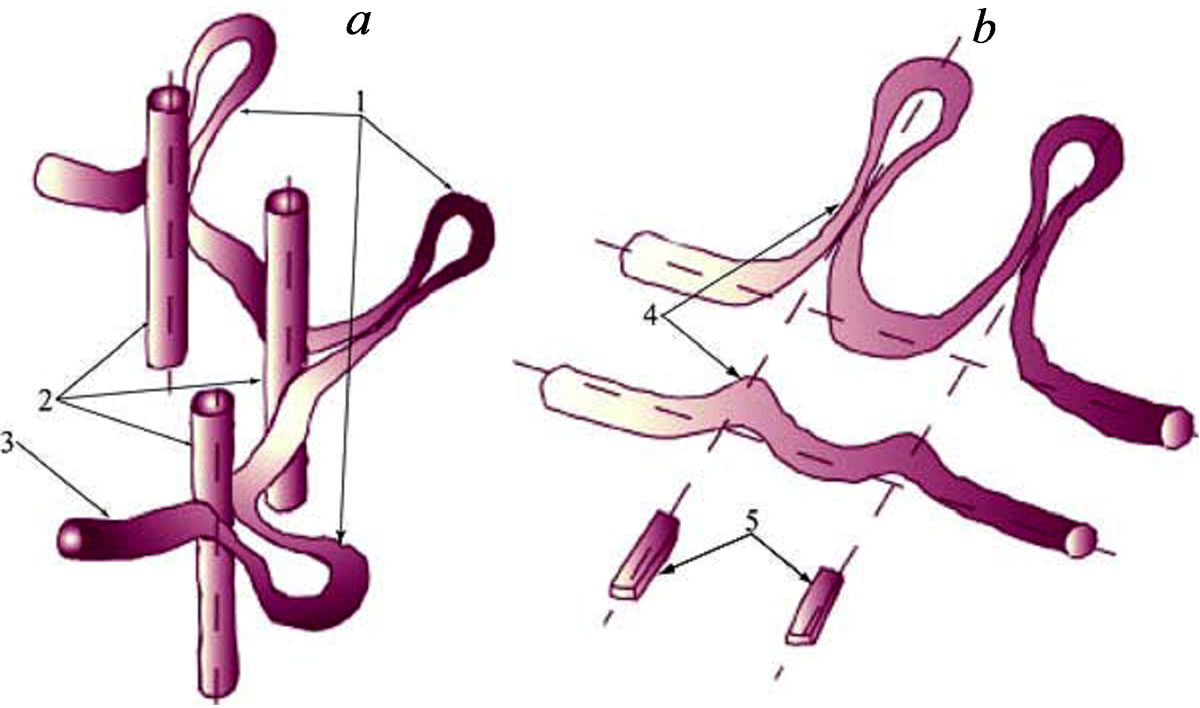
Figure 4. Three-dimensional deformation of the ring vortex (a) as compared to that of the Tollmien-Schlichting wave in a boundary layer (b): 3D bursts (1), longitudinal disturbances (2), ring vortex (3), 3D distortion of the 2D instability wave (4), roughness elements (5).

Figure 5. Smoke visualization of the jet cross sections at x/h = 0.5, 2.5, 4.5, 6.5 and 8.5 from the nozzle exit (left to right); nozzle width h = 10 mm, jet core velocity U0 = 3 m/s, Reh = 2000.

Figure 6. Mean velocity distributions in the near field of the jet: the free shear layer (a) and the near-wall layer (b); Reh = 5700.

Figure 7. Visualization of the wall plane jet in natural conditions: streamwise (a) and cross (b) sections; Reh = 5700.
3.4. Acoustic Effect on the Flow Pattern
Acoustic forcing of the laminar wall jet modifies the Kelvin-Helmholtz instability of the free shear layer. As a result, evolution of the coherent vortices and their interaction with the longitudinal structures depend on the oscillation frequency, Figure 9. In this example, the jet is subjected to sound waves radiated by a loudspeaker

Figure 8. Modulation of the free shear layer (a) and of the boundary layer (b): mean velocity disturbance as isosurface levels corresponding to ± 6% of U, positive and negative values are in dark blue and red (top) and in yellow and blue (bottom); Reh = 5700.

Figure 9. Velocity perturbations of the free shear layer of the jet disturbed by the longitudinal structures under acoustic forcing: f = 200 Hz, x/h = 3.7, isosurface levels are ± 0.3 U0 (a); f = 700 Hz, x/h = 1.9, isosurface levels are ± 0.4 U0 (b); positive and negative values are in red and blue; Reh = 5700.
placed above the jet at the nozzle exit plane. The hotwire results indicate that under the excitation at f = 200 Hz three-dimensional effects are less pronounced than at f = 700 Hz when three-dimensional flow structures at the transition to turbulence are well seen.
4. Round Jet Instability Affected by Initial Conditions
Obviously, evolution of the round jet depends on the initial conditions at the nozzle outlet. In particular, varying the nozzle geometry and, hence, the velocity distribution at the jet origin it is possible to control instability and dynamics of the laminar flow [17].
4.1. Round Jet with a Top-Hat Velocity Profile
In the case of a thin shear layer at the jet periphery, a substantial contribution to the laminar flow breakdown is that of the ring vortices rolling up close to the nozzle exit and interacting with the longitudinal structures of perturbations. This was already noted in Section 2, see also Figure 10.
4.2. Round Jet with a Parabolic Velocity Profile
The flow pattern is completely different at the initial parabolic mean velocity distribution created by special profiling of the nozzle, Figure 11. The jet becomes much more stable as compared to the top-hat configuration so that the laminar region spreads far downstream. In the present example, the laminar flow without visible perturbations is observed behind the nozzle outlet at a distance ten times larger than the nozzle diameter. Note-worthy is a negligible response of the laminar part of the jet to external acoustic forcing, if any. As is found in the present conditions, the flow characteristics are not affected, at least, at the sound frequencies up to several kilohertz and the pressure level up to 100 dB.
5. Origination and Evolution of Coherent Structures in Laminar and Turbulent Round Jets: A Comparison
Experimental data testify to similarities of the perturbed flow patterns of laminar and turbulent round jets. Also, almost one and the same response of the jets to external acoustic oscillations is found [18].
5.1. Laminar Round Jet
One more illustration of the laminar round jet evolution is given in Figure 12 where one can observe the ring vortices interacting with the controlled longitudinal perturbations similar to that presented in Subsections 2.1 and 4.1.
5.2. Turbulent Round Jet
In the same way, visualization of the jet with a turbulent mean velocity profile at the nozzle exit is demonstrated
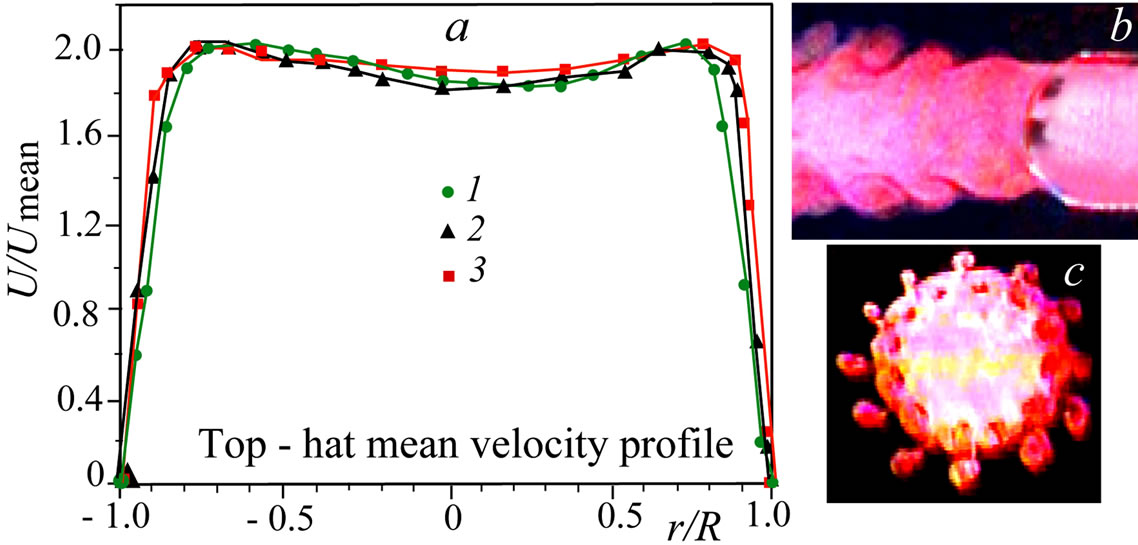
Figure 10. Distributions of mean velocity in the jet cross sections at x/d = 0.1 (1), 0.5 (2), and 1.0 (3) (a); ring vortices (b); 3D bursts spaced over the azimuthal coordinate due to interaction of the vortices with the streaky structures (c); Red = 6500.
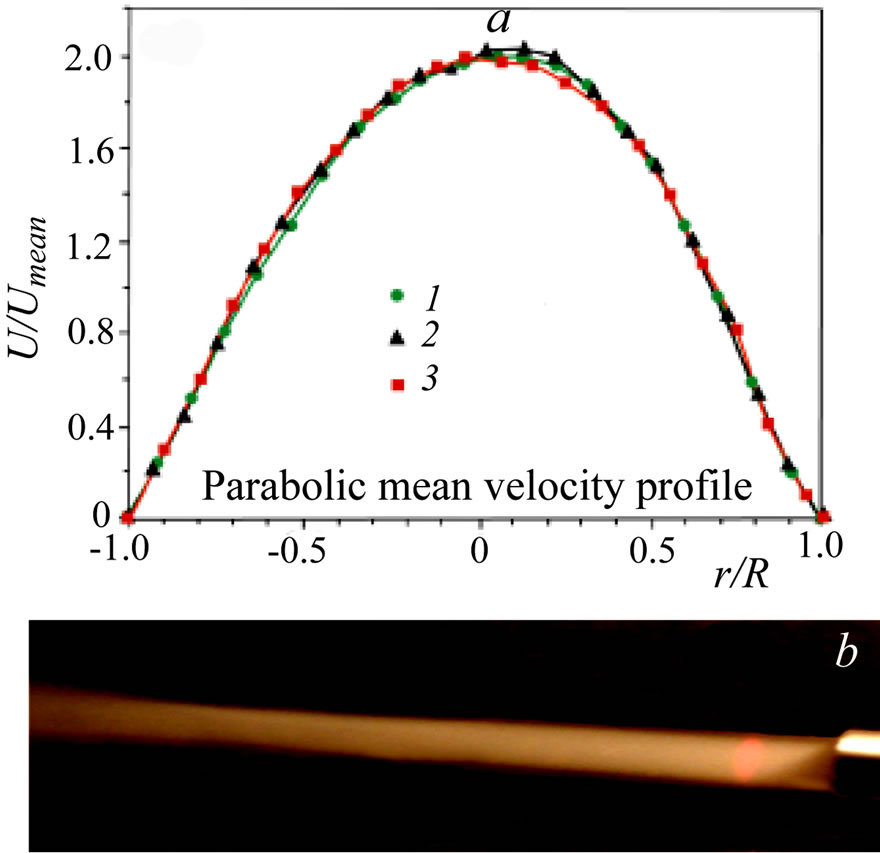
Figure 11. Distributions of mean velocity in the jet cross sections at x/d = 0.1 (1), 0.5 (2), and 1.0 (3) (a); laminar part of the jet at flow visualization (b); Red = 6500.

Figure 12. Dynamics of the laminar round jet: general view (a); streamwise section with the ring vortices (b); cross sections at different streamwise position (c); Red = 5200.
in Figure 13. The flow structure is not so pronounced as compared to the laminar jet, however, the ring vortices and the longitudinal perturbations are still found there. Thus, both laminar and turbulent jets are dominated by the generation of the ring vortices and the longitudinal structures interacting with each other.
5.3. Response to Acoustic Oscillations
To compare the receptivity of the laminar and turbulent jets to external acoustic excitation, they are forced by

Figure 13. Dynamics of the turbulent round jet: general view (a); streamwise section with the ring vortices (b); cross sections at different streamwise position (c); Red = 5200.
weak harmonic oscillations radiated by a loudspeaker transversally to the flow direction. Maximum amplitudes of the vortical perturbations excited at a fixed sound pressure level are presented in several cross sections in Figure 14. Here the data acquired in the jet shear layer are shown; the disturbances of the core region are much lower and not included. In both cases one can observe virtually the same amplitude of the ring vortices originating in the jets at the forcing frequency.
6. Dynamics of Laminar and Turbulent Plane Jets: A Comparison
Unstable plane jets experience periodic motion in different conditions of their origination. It turns out that the characteristics of large-scale oscillations are practically the same in laminar and turbulent flows [19].
6.1. Laminar Plane Jet with a Parabolic Mean Velocity Profile
Amplifying oscillations of laminar plane jets are associated with symmetric and anti-symmetric instability modes. The second of them prevails at the mean velocity profile tending to a parabolic one. An illustration is given in Figure 15 where the jet is visualized in natural conditions and under controlled acoustic excitation with different frequencies at a constant sound pressure level. The low-frequency forcing (Images b to e) stabilizes the antisymmetric disturbances and makes them more pronounced as compared to that in natural conditions (Image a). At increase of the excitation frequency, the oscillations become visible at a larger distance from the nozzle outlet and even turn to the symmetric mode (Image g).
6.2. Turbulent Plane Jet
Similarly to Figure 15, the flow patterns of turbulent plane jet are shown in Figure 16. In this case, the antisymmetric perturbations induced by acoustic excitation
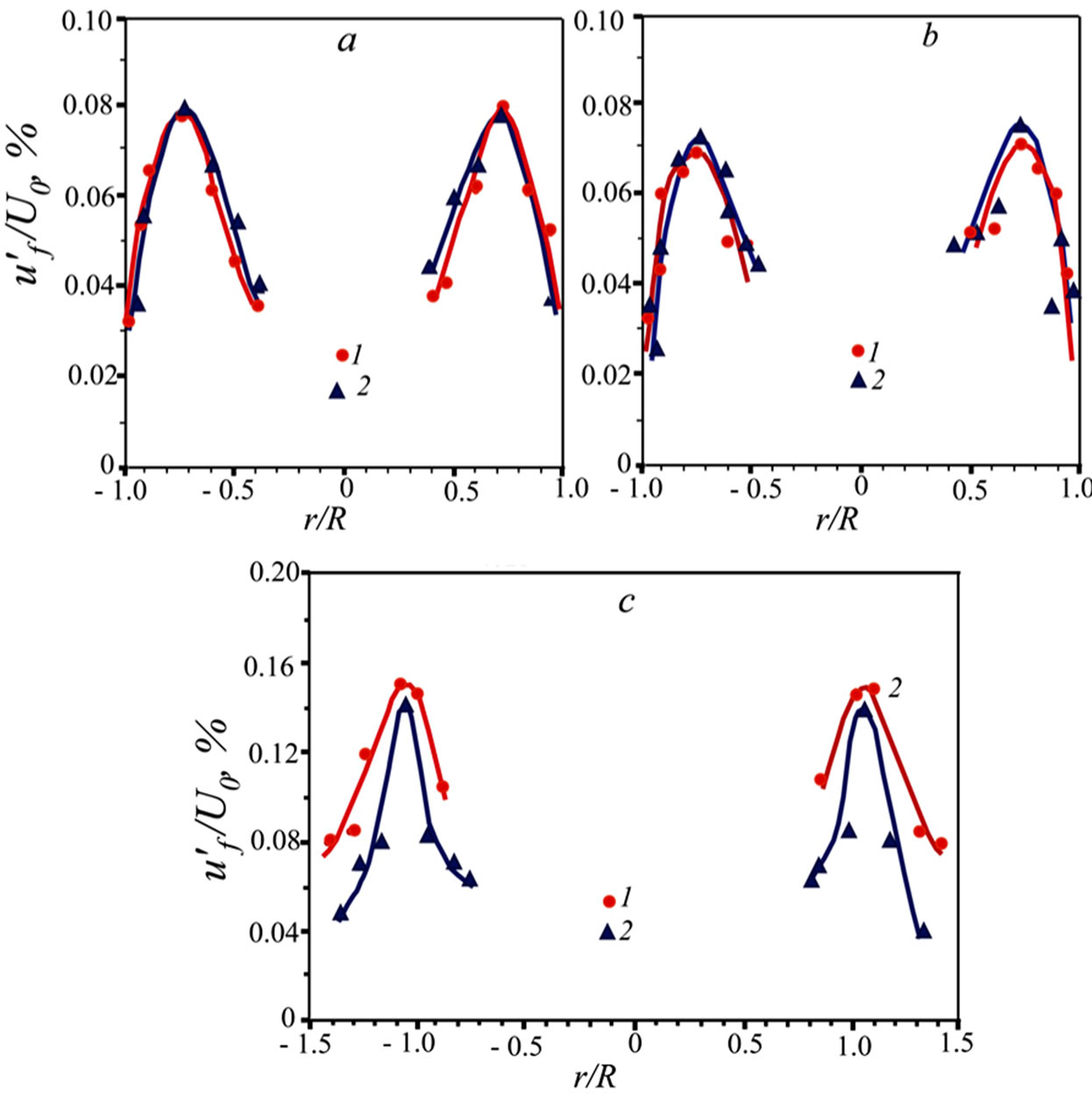
Figure 14. Amplitude distributions of the excited flow perturbations in cross sections of the turbulent (1) and laminar (2) jets at x/d = 0.1 (a), 0.25 (b), and 1.0 (c); excitation frequency f = 180 Hz, Red = 5200.
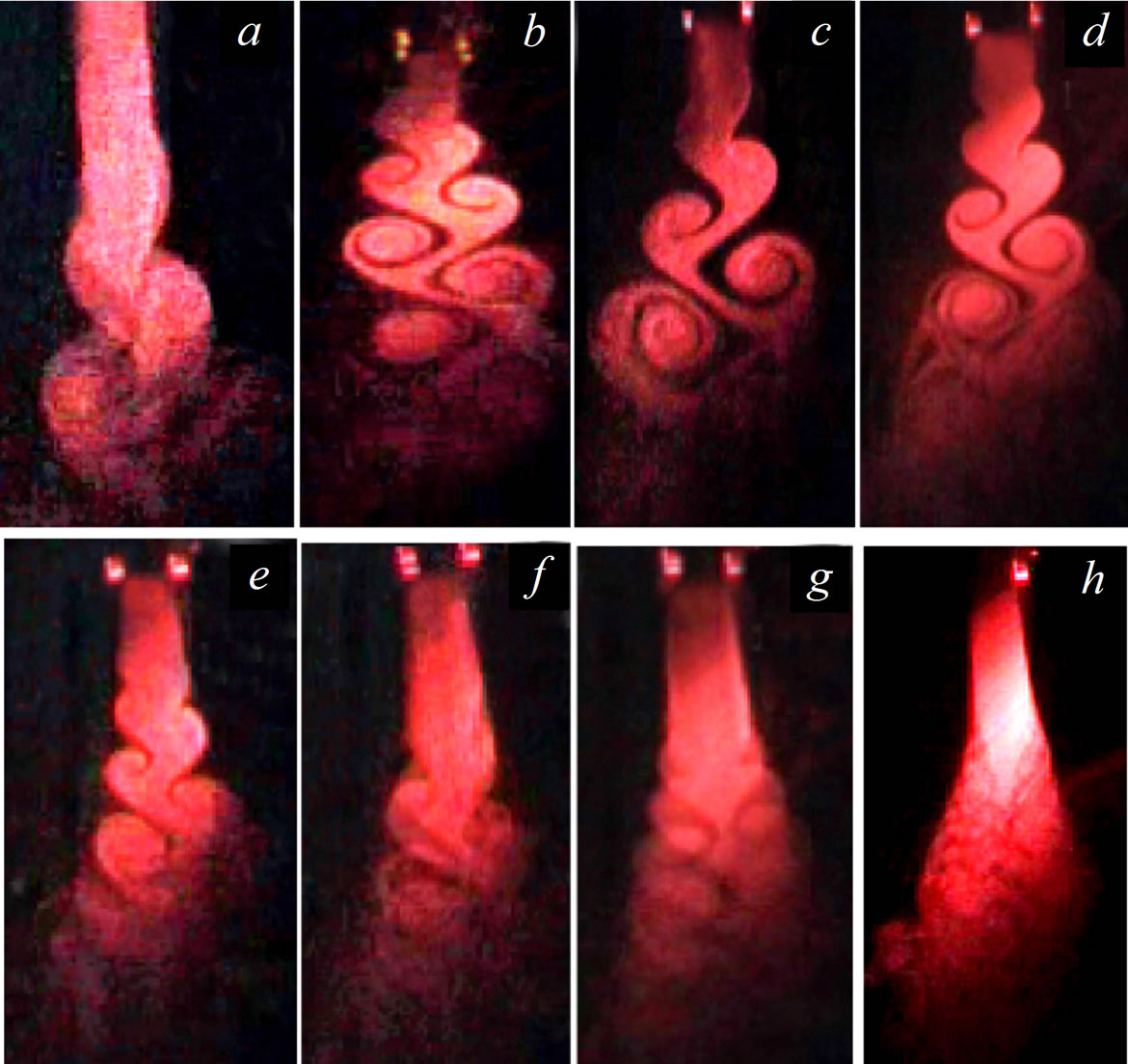
Figure 15. Visualization of the laminar plane jet with a parabolic mean velocity distribution in natural conditions (a) and under external acoustic forcing at frequencies f = 30 (b), 40 (c), 50 (d), 60 (e), 70 (f), 90 (g), and 150 Hz (h); Reh = 3300.
are clearly demonstrated by Images b to e while the flow periodicity is not observed at visualization in natural conditions (Image a). Most likely, this is due to high-amplitude background velocity disturbances overwhelming the coherent motion which is less pronounced in the absence of external forcing.
At a fixed frequency of sound waves characteristics of the generated vortical disturbances, i.e., their wave length

Figure 16. Visualization of the turbulent plane jet in natural conditions (a) and under external acoustic forcing at frequencies f = 30 (b), 40 (c), 50 (d), and 60 Hz (e); Reh = 3300.
and propagation velocity in the laminar and turbulent jets are close to each other. These data testify to the sinusoidal oscillations of plane jets as a fairly universal phenomenon, at least, at their external periodic forcing.
7. Round Jet in a Crossflow
The unstable behavior of a round jet is substantially modified by a cross flow. Some features of the interaction between the jet and the transverse velocity component are demonstrated by the following visualization results [20].
The laminar round jet with a parabolic mean velocity profile injected from the wall normally to a flat-plate boundary layer is shown in Figure 17. The data are obtained at the jet core velocity about three times larger than the maximum cross-flow velocity at the edge of the boundary layer. The jet contour is distinctly seen and remains stable near the wall. In this region the flow which is initially axisymmetric at the jet origin turns to a pair of stationary counter rotating vortices as is shown in Figure 18.
Instability of such vortex configuration results in the nonstationary perturbations which are observed in the top of Figure 17. More details on their spatial arrangement obtained under acoustic forcing of the jet are presented in Figure 19. The mushroom-like bursts of disturbances seem to develop separately on each of the counter rotating vortices that is somewhat different from the results of global stability analysis [9] testifying to high-frequency oscillations surrounding the entire stationary vortex structure. Anyhow, the above crossflow effects on the round jet are in overall agreement with the numerical data.
Also, the present data on the jet transformation into
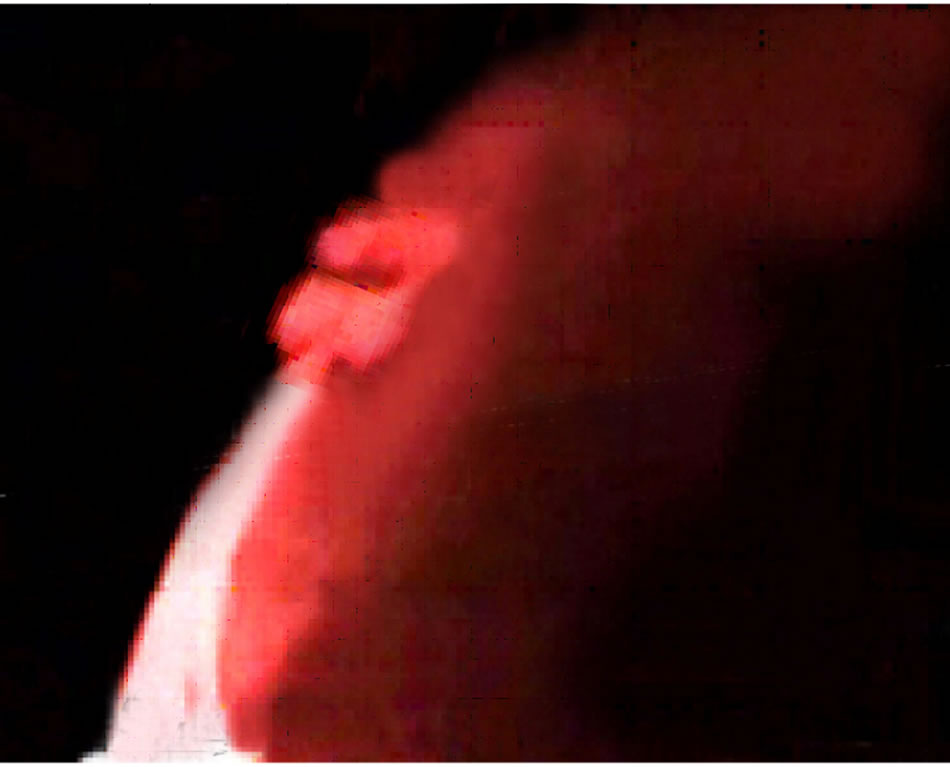
Figure 17. Laminar round jet emanating from a flat-plate surface into the boundary layer; Red = 950.
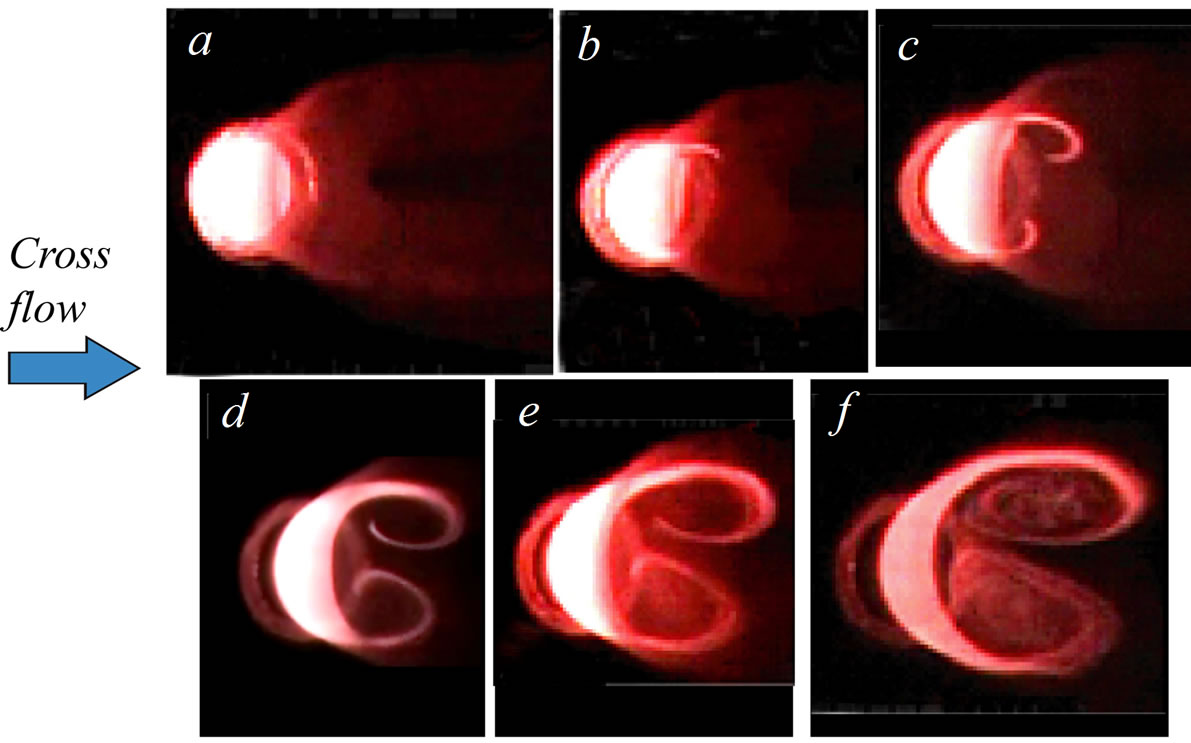
Figure 18. Stationary vortices visualized in the jet cross sections while moving away from the nozzle outlet: images (a) to (f).
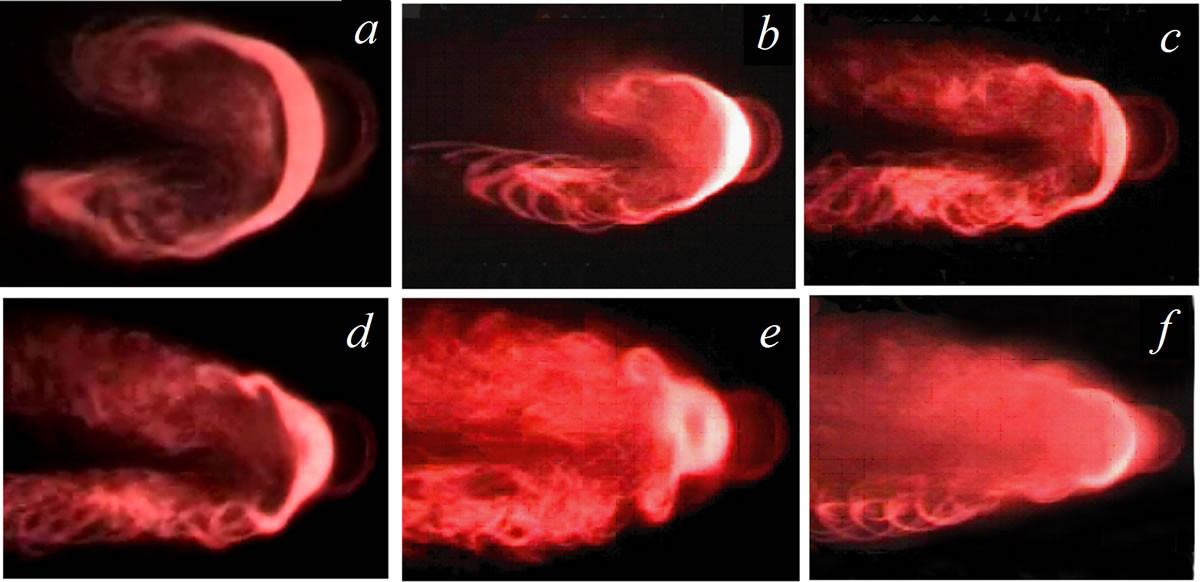
Figure 19. Nonstationary disturbances in the jet cross sections: images (b) to (f) are taken when increasing the wallnormal distance at the 30-Hz acoustic excitation.
stationary counter rotating vortices in the near-wall region and the following amplification of nonstationary velocity perturbations are consistent with previous experimental findings. In particular, the main features of flow patterns shown in Figures 17 and 18 are much similar to those observed at visualization of a round jet in crossflow in a water channel [8].
8. Micro Jets in a Transverse Acoustic Field
The term “micro” applies here to the jets at their transverse scale as small as a fraction of millimeter. In such conditions, a profound influence of external acoustic forcing upon the jet evolution is revealed through its visualization [21,22].
Two phenomena at the micro jet excitation by sound waves are illustrated in the following figures. One of them is flattening of the round jet and its transformation into a plane one subjected to large-scale sinusoidal oscillations (see Figure 20). The modification of the jet by sound waves is obviously much stronger than the acoustic effects on laminar round jets usually found such as variation of the vortex passage frequency and acceleration of the laminar flow breakdown. In the present case, the entire flow structure is completely different from that in natural conditions.
Another phenomenon to be noticed is splitting of the round jet into two ones perturbed by small-scale periodic disturbances as is shown in Figures 21 and 22. The effect is fairly universal in wide ranges of the Reynolds number and the forcing frequency.
9. Final Comment
As is shown by the above experimental results, the lowReynolds-number jets experience a variety of instability phenomena. Their contribution to the flow dynamics depends strongly on conditions of the jet origination pro-
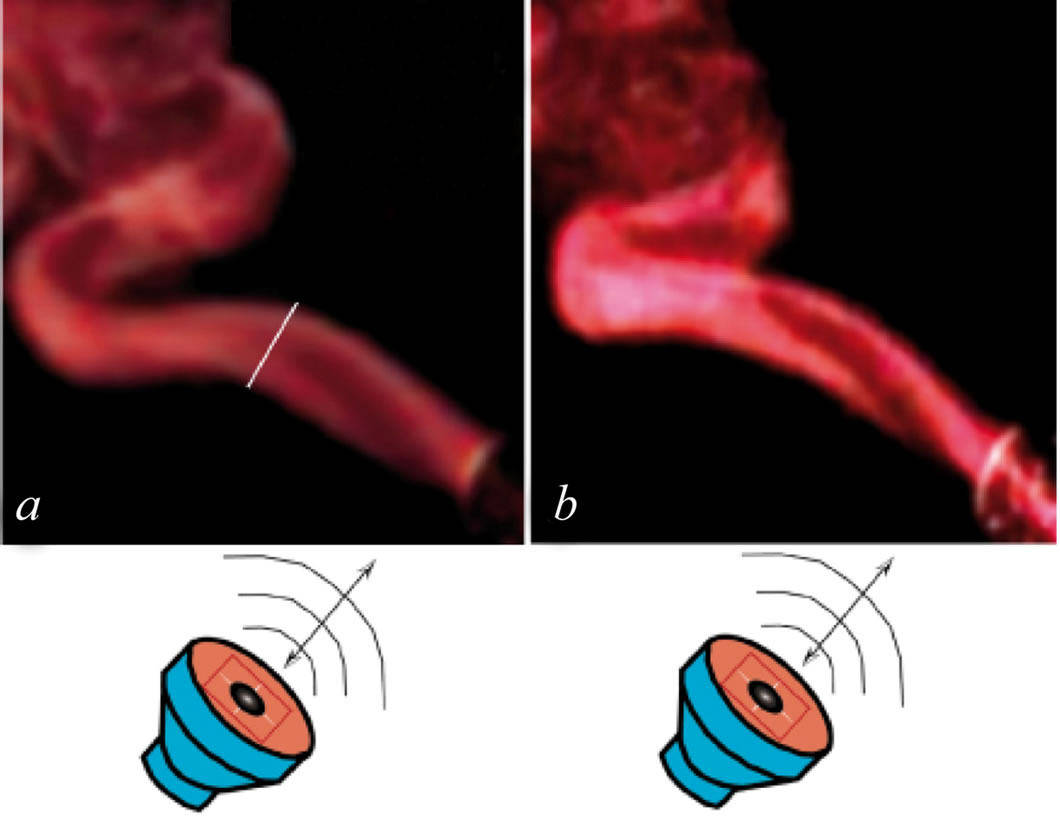
Figure 20. Smoke visualization of the round micro jet affected by transverse acoustic oscillations at 40 Hz (a) and 100 Hz (b); sound pressure level is 90 dB, nozzle diameter d = 1600 μm, Red = 60.
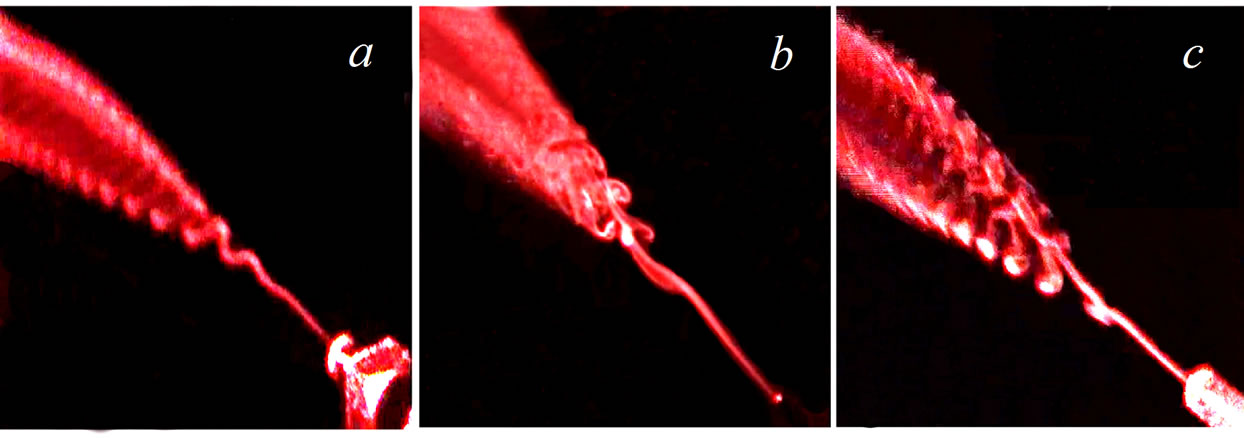
Figure 21. Visualization of the round micro jet under the 200-Hz acoustic forcing at different diameter of the nozzle outlet: d = 200 μm, Red = 20 (a), 400 μm, 40 (b), and 500 μm, 50 (c).
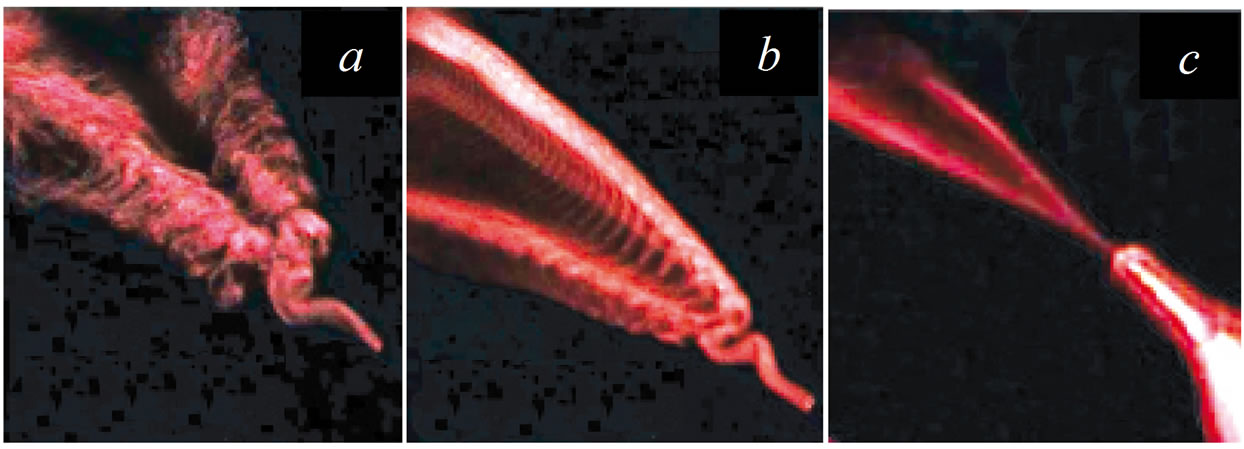
Figure 22. Visualization of the round micro jet at d = 500 μm, Red = 50 varying the excitation frequency as f = 40 Hz (a), 150 Hz (b), and 1500 Hz (c).
viding individual features of macro and micro, round and plane jets. However, a quality of the unstable jets occurring at different Reynolds number and the basic flow configurations are their pronounced responses to stationary and nonstationary external disturbances. As a result, flow characteristics can be easily modified and controlled even by small-amplitude perturbations.
10. Acknowledgements
This work was supported by the Integration project SB RAS No. 24 and the Russian Foundation for Basic Research, projects Nos. 11-01-00292,12-08-31083, 12-07- 00548, 13-07-00616.
REFERENCES
- A. J. Yule, “Large-Scale Structure in the Mixing Layer of a Round Jet,” Journal of Fluid Mechanics, Vol. 89, 1978, pp. 413-432. http://dx.doi.org/10.1017/S0022112078002670
- D. Liepmann and M. Gharib, “The Role of Streamwise Vorticity in the Near-Field Entrainment of Round Jets,” Journal of Fluid Mechanics, Vol. 245, 1992, pp. 643-668. http://dx.doi.org/10.1017/S0022112092000612
- A. J. Yule, “Large-Scale Structure in the Mixing Layer of a Round Jet,” Journal of Fluid Mechanics, Vol. 89, 1978, pp. 413-432. http://dx.doi.org/10.1017/S0022112078002670
- J. Cohen and I. Wignanski, “The Evolution of Instabilities in Axisymmetric Jet. Pt. 1. The Linear Growth of Disturbances near the Nozzle,” Journal of Fluid Mechanics, Vol. 176, 1987, pp. 191-219. http://dx.doi.org/10.1017/S0022112087000624
- H. Sato, “The Stability and Transition of a Two-Dimensional Jet,” Journal of Fluid Mechanics, Vol. 7, No. 1, 1960, pp. 53-80. http://dx.doi.org/10.1017/S0022112060000049
- A. K. M. F. Hussain and C. A. Thompson, “Controlled Symmetrical Perturbation of the Plane Jet: An Experimental Study in the Initial Region,” Journal of Fluid Mechanics, Vol. 100, 1980, pp. 397-431. http://dx.doi.org/10.1017/S002211208000122X
- T. T. Lim, T. H. New and S. C. Luo, “On the Development of Large-Scale Structures of a Jet Normal to a CrossFlow,” Physics of Fluids, Vol. 13, No. 3, 2001, pp. 770- 775. http://dx.doi.org/10.1063/1.1347960
- T. H. New, T. T. Lim and S. C. Luo, “Effects of Jet Velocity Profiles on a Round Jet in Cross-Flow,” Experiments of Fluids, Vol. 40, No. 3, 2006, pp. 859-875. http://dx.doi.org/10.1007/s00348-006-0124-y
- S. Bagheri, Ph. Schlatter, P. J. Schmid and D. S. Henningson, “Global Stability of Jet in Crossflow,” Journal of Fluid Mechanics, Vol. 624, 2009, pp. 33-44. http://dx.doi.org/10.1017/S0022112009006053
- G. Chie, C. H. Shen and Z. B. Wang, “Peculiar Phenomenon of Micro-Free-Jet Flow,” Physics of Fluids, Vol. 21, No. 1, 2009, pp. 092001-1-092001-13. http://dx.doi.org/10.1063/1.3224012
- J.-B. Carpenter, F. Baillot, J.-B. Blaisot and C. Dumouchel, “Behavior of Cylindrical Liquid Jets Evolving in a Transverse Acoustic Field,” Physics of Fluids, Vol. 21, No. 023601, 2009, pp. 1-15.
- C. J. Chang, C. H. Shen and C. Gau, “Flow and Heat Transfer of a Micro Jet Impinging on a Heated Chip: Part I— Micro Free and Impinging Jet Flow,” Nanoscale and Microscale Thermophysical Engineering, Vol. 17, No. 1, 2013, pp. 50-68.
- G. R. Grek, V. V. Kozlov and Yu. A. Litvinenko, “Stability of Subsonic Jets,” The Manual with CD-ROM Presentation, Novosibirsk State University, Novosibirsk, 2012, pp. 1-208.
- V. V. Kozlov, G. R. Grek, L. Loefdachl, V. G. Chernoray and M. V. Litvinenko, “Role of Localized Streamwise Structures in the Process of Transition to Turbulence in Boundary Layers and Jets (Review),” Journal of Applied Mechanics and Technical Physics, Vol. 43, No. 2, 2002, pp. 224-236.
- V. V. Kozlov, G. R. Grek, G. V. Kozlov and M. V. Litvinenko, “Visualization of the Processes of Evolution and Turbulent Breakdown of a Low-Speed Round Jet,” Visualization of Mechanical Processes, Vol. 1, No. 2, 2011, pp. 1-18.
- A. V. Boiko, H. H. Chun, M. V. Litvinenko, V. V. Kozlov, E. E. Cherednichenko and I. Li, “About Longitudinal Structures in a Plane Jet,” Doklady Physics, Vol. 403, No. 1, 2005, pp. 1-3.
- G. V. Kozlov, G. R. Grek, A. M. Sorokin and Yu. A. Litvinenko, “Initial Conditions Effect at the Nozzle Exit on the Round Jet Structure,” Thermophysics and Aeromechanics, Vol. 15. No. 1, 2008, pp. 59-68. http://dx.doi.org/10.1134/S0869864308010046
- G. V. Kozlov, Yu. A. Litvinenko, G. R. Grek and A. M. Sorokin, “About Mechanism of the Coherent Structures Origin and Downstream Evolution in the Laminar and Turbulent Round Jets,” Vestnik Novosibirsk State University, Series: Physics (in Russian), Vol. 3, No. 1, 2008, pp. 12-22.
- V. V. Kozlov, G. R. Grek, Y. A. Litvinenko, G. V. Kozlov and M. V. Litvinenko, “Influence of Initial Conditions at the Nozzle Exit and Acoustical Action on the Structure and Stability of a Plane Jet,” Visualization of Mechanical Processes, Vol. 2, No. 3, 2012, pp. 1-29.
- G. R. Grek, G. V. Kozlov, V. V. Kozlov, Y. A. Litvinenko and M. V. Litvinenko, “Round Jet in a Cross Shear Flow,” Visualization of Mechanical Processes, Vol. 2, No. 4, 2012, pp. 1-29.
- V. V. Kozlov, G. R. Grek, Yu. A. Litvinenko, G. V. Kozlov and M. V. Litvinenko, “Round and Plane Jets in a Transverse Acoustic Field,” Journal of Engineering Thermophysics, Vol. 20, No. 3, 2011, pp. 272-289. http://dx.doi.org/10.1134/S1810232811030052
- Yu. A. Litvinenko, G. R. Grek, V. V. Kozlov and G. V. Kozlov, “Subsonic Round and Plane Macro-Jets and MicroJets in a Transverse Acoustic Field,” Doklady Physics, Vol. 56, No. 1, 2011, pp. 26-31. http://dx.doi.org/10.1134/S1028335811010046
NOTES
*Review paper.

