Open Journal of Earthquake Research
Vol.04 No.03(2015), Article ID:59214,12 pages
10.4236/ojer.2015.43010
On the Imminent Regional Seismic Activity Forecasting Using INTERMAGNET and Sun-Moon Tide Code Data
Strachimir Cht. Mavrodiev1, Lazo Pekevski2, Giorgi Kikuashvili3, Emil Botev4, Petar Getsov5, Garo Mardirossian5, Georgi Sotirov5, Dimitar Teodossiev5
1Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
2University “Sts. Cyril and Methodius”, Seismological Observatory, Skopje, Macedonia
3Ilya State University, Tbilisi, Georgia
4National Institute for Geophysics, Geography and Geodesy, Bulgarian Academy of Sciences, Sofia, Bulgaria
5Space Research and Technology Institute, Bulgarian Academy of Sciences, Sofia, Bulgaria
Email: schtmavr@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2015; accepted 24 August 2015; published 27 August 2015
ABSTRACT
In this paper we present an approach for forecasting the imminent regional seismic activity by using geomagnetic data and Earth tide data. The time periods of seismic activity are the time periods around the Sun-Moon extreme of the diurnal average value of the tide vector module. For analyzing the geomagnetic data behaviour we use diurnal standard deviation of geomagnetic vector components F (North, East, Down) for calculating the time variance GeomagSignal. The Sun storm influence is avoided by using data for daily A-indexes (published by NOAA). The precursor signal for forecasting the incoming regional seismic activity is a simple function of the present and previous day GeomagSignal and A-indexes values. The reliability of the geomagnetic “when, regional” precursor is demonstrated by using statistical analysis of day difference between the times of “predicted” and occurred earthquakes. The base of the analysis is a natural hypothesis that the “predicted” earthquake is the one whose surface energy density in the monitoring point is bigger than the energy densities of all occurred earthquakes in the same period and region. The reliability of the approach was tested using the INTERMAGNET stations data located in Bulgaria, Panagurishte, PAG (Jan 1, 2008-Jan 29, 2014), Romania, Surlari, SUA (Jan 1, 2008-Jan 27, 2014), Italy, L’Aquila, AQU (Jan 1, 2008-May 30, 2013) in the time of EU IRSES BlackSeaHazNet (2011-2014) project. The steps of program for solving the “when, where and how” earthquake prediction problem are shortly described.
Keywords:
Earthquakes, Geomagnetism, Earth Sun-Moon Tide, Regional Seismic Activity, Forecasting

1. Introduction
The problem of “when, where and how” earthquake prediction cannot be solved only on the basis of geodetic data [1] -[6] . The possible triggering of the earthquakes by the tidal has been investigated for a long period of time [7] - [14] . The conclusion that the earthquake’s time is correlated with the tidal extremes is not unique, because in some of the extremes there are no earthquakes. The inclusion of additional information in the analysis, for example the Earth’s electrical currents’ signals, permits one to estimate the most probable time of incoming earthquakes [15] - [17] .
As more accurate space and time measuring set for the Earth’s crust condition parameters, including in the monitoring of the measurements of the electromagnetic fields under, on and over the Earth’s surface, the temperature distribution and other possible precursors can be useful for the study of the “when, where and how” predictions of earthquakes. For example, in the papers [18] - [20] , the possibility for short-term earthquake prediction in Greece by seismic electric signals was investigated.
The atmospheric and ionosphere electromagnetic phenomena associated with earthquakes were analyzed in many books and papers [21] - [26] and the future direction of the investigation related to earthquake prediction was proposed, as well as its practical application to some events. The papers [27] [28] concern the observations of electromagnetic radiation in the LF and VLF ranges related to the occurrence of an earthquake.
Тhe paper [29] presents the results of the complex investigation of the variations of crust electrical resistivity as a function of tidal deformations on the basis of an extremely low-frequency radio station, which could be more promising for increasing the reliability of electromagnetic-based earthquake predictions. In the papers [30] [31] the electromagnetic anomalies in a wide range of radio frequencies from ULF, VLF to VHF, which had been observed before some destructive earthquakes in continental Greece, are presented.
The impressive results of the modified VAN method are presented in papers and via web sites [15] -[17] [32] [33] , where the appropriate measuring of electric Earth signals is analyzed. Their analysis demonstrates that the direction to the epicentre of incoming earthquakes can be estimated and the time is defined from the next extreme of tidal potential. Some possible geophysical models of the phenomena are proposed and the prediction of the future magnitude is analyzed.
On the web site [34] and in the papers cited there, the results of electropotential monitoring, based on the especially constructed electrometer and the appropriate temporal data acquisition system, are presented.
One has to mention the satellite possibilities for monitoring the radiation activity of the Earth’s surface for discovering the anomalies, which should be earthquake precursors [35] .
The analyses of the data from satellite monitoring for the ionosphere and the Earth’s radiation belt parameters also give evidence for anomalies which can be interpreted as earthquake precursors. The information concerning the latest results of the developing of earthquake precursor research can be found on the conference sites [36] [37] .
The data for the connection between an incoming earthquake and meteorology effects like quasi-stationary earthquake clouds can be seen on the website [38] . The statistic since 1993 for the prediction reliability is also represented together with some theoretical models and estimations.
To summarize, one can say that the standard geodetic monitoring [5] , the monitoring of different components of the electromagnetic field under, on and over the Earth’s surface, some of the atmospheric anomalies and the behaviour of charge distribution in the Earth’s radiation belts (see, for example [39] [40] ), sometimes can serve as earthquake’s precursors.
The progress in the electromagnetic quake earthquake precursor approach was presented in papers [41] -[48] . The earthquake part of the model can be repeated in many time ways “theory-experiment-theory”, using nonlinear inverse problem methods for discovering unknown dependences and correlations between different geophysical fields in dynamically changed spaces and times scales.
It seems obvious that the problem of adequate physical understanding of the correlations between electro- magnetic precursors, tidal extremes and incoming earthquakes is connected with the progress of creating the adequate Earth’s magnetism model.
The achievement of the Earth’s surface tidal potential modelling, which includes the ocean and atmosphere tidal influences, is an essential part of the research. In this sense the comparison of the Earth tides codes― ANALYZE, ETERNA-package, the version 3.30 [49] ; BAYTAP-G code in the version from November, 15, 1999 [50] -[52] ; VAV code (version from April 2002) [53] [54] , is very hard but helpful work.
The role of geomagnetic variations as a precursor could be explained by the obvious hypothesis that during the time before the earthquakes, the crust strain, deformation or displacement changes in a certain interval of density volume change, where the chemical phase shift arises, lead to electrical charge shift. The increasing of the electro potential leads to the increasing of the regional Earth currents which influence the geomagnetic field variability. The Fourier analysis of the geomagnetic field gives the time period of alteration in minute scale. We call such a specific geomagnetic variation a geomagnetic quake.
The piezo-effect model for electrical currents cannot explain the alternations due to its linearity.
The K-index [55] , accepted for the estimation of the geomagnetic conditions, cannot indicate well the local geomagnetic variation for a minute time period, because it is calculated on the basis of 3-h data. Nevertheless, the K-index behaviour in the near space has to be analyzed because of the possible Sun-wind influence on the local behaviour of the geomagnetic field. If the geomagnetic field components are measured many times per second, one can calculate the frequency dependence of full geomagnetic intensity and analyze the frequency spectrum of the geomagnetic quake. If the variations are bigger than the usual for a certain period of time, one can say that we have a geomagnetic quake, which can be possible earthquake’s precursor. The nonlinear inverse problem analysis for 1999-2001 of the geomagnetic and earthquake data for Sofia region gives the estimation that the probability time window for the predicted earthquake (event, events) is approximately ±2 days for the next minimum of the Earth’s tidal potential and ±2.7 days for the maximum [47] .
The future epicentre coordinates can be estimated according to the data from at least 3 points of measuring the geomagnetic vector, using the inverse problem methods, applied for the estimation of the coordinates of the volume, where the chemical phase shift (dehydration) arrived in the framework of its time window.
In the case of an incoming big earthquake (magnitude > 5 - 6), the changes of vertical electropotential distribution, the Earth’s temperature, the infrared Earth’s radiation, the behaviour of the water sources, its chemistry and radioactivity (222 Rn), the atmospheric conditions (earthquake clouds, etc.) and the charge density of the Earth’s radiation belt, have to be dramatically changed near the epicentre area.
The achievements of the tidal potential modeling of the Earth’s surface, including the ocean and atmospheric tidal influences, the multi-component correlation analysis and the nonlinear inverse problem methods in fluid’s dynamics and electrodynamics are crucial for every single step of the construction of mathematical and physical models.
2. Methodology: The Number Comparison of Two Time Experimental Series
If we need to estimate the variability of one experimental series of measurements’ data
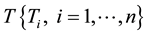 we can calculate the mean value
we can calculate the mean value
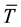 :
:
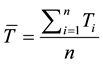 (1)
(1)
and to calculate the value of its dimensionless standard deviation SdT:
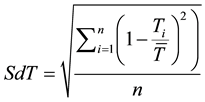 (2)
(2)
When one needs to compare the variability of two time experimental series Tij, i = 1, 2; j = 1, , nj, we have to calculate the its mean value
, nj, we have to calculate the its mean value
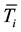 and SdTi according formulae (1) and (2).
and SdTi according formulae (1) and (2).
Obviously, the biggest standard deviation value means the biggest variability of the series.
3. The Forecasting of Imminent Regional Seismic Activity on the Basis of the Geomagnetic and Sun-Moon Tide Code Data
In this paragraph the data-acquisition system for archiving, visualization and analysis is presented [47] [56] [57] [59] .
3.1. Description of the Approach―Figure 1
The data used:
・ the Balkan Intermagnet geomagnetic stations PAG, Bulgaria, SUA, Romania, AQU, Italy, minute data (http://www.intermagnet.org/),
・ the software for calculation of the daily and minute Earth tide behaviour (Dennis Milbert, NASA), http://home.comcast.net/~dmilbert/softs/solid.htm),
・ the Earth tide extremes (daily average maximum, minimum and inflexed point) as a trigger of earthquakes,
・ the data for World A-indices (http:/www.swpc.noaa.gov/alerts/a-index.html).
3.2. The Variables from Figure 1
The simple mathematics for the calculation of the precursor signal, the software for illustrating the reliability of forecasting and its statistic estimation and the variables in Figure 1 are described in the next.
The variables
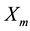 ,
,
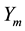 ,
,
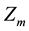 are the component of minute averaged values of the geomagnetic vector, m = 1440, and the variables
are the component of minute averaged values of the geomagnetic vector, m = 1440, and the variables
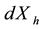 ,
,
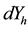 ,
,
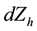 are standard deviation of
are standard deviation of
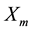 ,
,
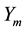 ,
,
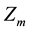 , calculated for 1 hour (h = 1,
, calculated for 1 hour (h = 1,
 , 24):
, 24):

where:
Figure 1. Reliability of the approach for the PAG INTERMAGNET station located in Bulgaria.

The geomagnetic signal


The A indices are the Low, Medium and High a-indices calculated by the NOAA, Space weather prediction center: http://www.swpc.noaa.gov/alerts/a-index.html. In the approach we use the Alow;
The variable GmSigday is the diurnal mean value of GmHourSigh:

and

The indices of earthquake’s magnitude value are the distance in hundred km between the epicentre and the monitoring point.
The variable SChtM is the modified earthquake’s surface energy density in the monitoring point:

The variable PerDenEqSum [J/km2] is the sum of variable

The variable SumEnergy [J/km2 per day] is the sum of the variable

One has to note that the explicit form of variable SChtM was established in the framework of inverse problem with condition to have more clear correlation between the variables

The variable TideMinute [cm] is the module of tide vector calculated every 15 minutes;
The variable TideDay [cm] is the diurnal mean value in time calculated in the analogy of mass centre formulae

Note: for seconds and more samples per second the generalization has to calculate geomagnetic field characteristics for every minute and correspondingly the values of GmSigday have to be the average for 1440 minutes.
The positive value of variable

In the Figure 1 the values of variable PerDenEqSum are calculated not only in the time periods around extremes but also in the time period between them. It is seen that the values in the extreme periods are bigger.
The use of above described analysis for longer time period with calculation of distribution of day difference between “predicted” earthquakes (earthquakes with biggest value SChtM) in the frame work of special created data acquisition system demonstrates the reliability of the approach for forecasting of imminent regional seismic activity.
4. The Reliability of the Approach Using INTERMAGNET Data from Stations Located in Bulgaria, Romania and Italy
The distribution of differences between the times of the “predicted” and occurred earthquakes can serve as statistical proof for the reliability of the forecasting of imminent regional seismic activity. As a definition of a “predicted” earthquake, we use the natural hypothesis that it is the earthquake with biggest value of variable among all the earthquakes occurred in the region with a radius of 700 km. The distribution of day differences is presented for Intermagnet data stations PAG, Panagurishte, Bulgaria, SUA, Surlari, Romania and AQU, L’Aquila, Italia. The corresponding data parameters and time periods are presented in the Figures 2-4.
As one can see from the Figure 2, the distribution is close to the Gauss one with hi2 = 0.89. The relation between the sums of SChtM for the predicted and occurred earthquakes is equal to r = 5.51/6.48. So, the reliability of regional imminent seismic forecasting has 85% probability for the PAG data.
As one can see from the Figure 3, the distribution is close to the Gauss one with χ2 = 0.92. The relation between the sums of SChtM for the predicted and occurred earthquakes is equal to r = 8.83/11.0. So, the reliability of regional imminent seismic forecasting has 80% probability for the SUA data.
As one can see from the Figure 4, the distribution is close to the Gauss one with hi2 = 0.87. The relation between the sums of SChtM for the predicted and occurred earthquakes is equal to r = 1.05/1.15. So, the reliability of regional imminent seismic forecasting has 91 % probability for the AQU data.
5. Some Examples of Imminent Regional Confirmation of Forecasting
Some examples (http://theo.inrne.bas.bg/~mavrodi):
・ Dusheti, Georgia flux gate second magnetometer―Mw 7.1, depth 7.2 km, 2011, 23 Oct, 36.63N, 43.49E, Van, Turkey earthquake;
Figure 2. Day difference distribution for PAG data and it Gauss fit.
Figure 3. Day difference distribution for SUA (Surlari, Romania) data and its Gauss fit.
Figure 4. Day difference distribution for AQU (L’Aquila Italy) data and its Gauss fit.
・ Skopje, Macedonia (second) and Panagurichte (minute) flux gate magnetometers―Mw 5.6, Depth 9.4 km, 42.66N, 23.01E, 00.00 hour, 22 May, 2012;
・ Grocka, Serbia and Panagurichte (minute) flux gate magnetometers―Mw 6.1, Depth 18 km, 26 Jan 2014, 13:55, 38.19N, 20.41E; Mw 6.0, depth 2 km, 3 Feb, 2014, 03:08, 38.25N, 20.32E, Mw 5.6, Depth 9.4 km.
During our investigation of the relation between the regional geomagnetic and seismic activity in the areas of interest it was found that in case of a strong earthquake occurred in the distances less than 700 km from the geomagnetic observatory, a clear precursor signal was evident.
6. Using the Daily Tide Extremes as Earthquakes Triggers
In this section we present an explanation why the geomagnetic quakes forecasting are reliable.
We introduce the variable DayDiff which is the difference between the time of earthquake and the time of nearest tide extreme:
Number of Earthquakes and

The distribution for 628,873 world earthquakes with magnitude M ≥ 3.5 of occurred since 1981 (International Seismological Center: http://www.isc.ac.uk/data) of variable DayDiff is presented in Figure 5. As one can see 92% of all analyzed earthquakes are occurred in the time period ±2.23 day around the time of tide extreme in their epicentres.
7. Proposal for Complex Program for Solving “When, Where and How” Earthquake’s Prediction Problem
For the solving step by step “when, where and how” earthquake prediction problem we need realization of project ([58] [59] (http://theo.inrne.bas.bg/~mavrodi/project.html)), [60] :
Step 1. Creating complex regional monitoring network with a real time data acquisition system for archiving, testing, visualizing and analyzing the data and the estimation risks, which includes: 3 stationary and one mobile geoelectromagnetic stations (1 - 10 samples per second), 3 - 5 water level boreholes (2 samples per hour), 5 - 7 stations for measure Radon (222 Rn) concentration (6 samples per day), the seasonal and independent daily data for the crust temperature (2 samples per day) and 3 - 4 multi-frequency sound vector receivers (6 samples per hour). Important note: the number of samples is preliminary estimated.
Step 2. Using the above data, the regional geological and seismic (especially foreshock) data, the ionosphere behaviour data to start formulating and solving the inverse problem for forecasting the time, the epicentre’s coordinates, the depth and the intensity of an incoming regional earthquake as well as for actualization of regional seismic risk estimation.
Such complex monitoring polygons can be created in Balkans, Ukraine and Caucasus for better practical using of EU IRSES BlackSeaHazNet project (2011-2014) results and qualified staff: BlackSeaHazNet results: http://cordis.europa.eu/result/rcn/148955_en.html [60] .
8. Conclusions
The correlation between local geomagnetic quakes and incoming earthquakes in the time window defined from the further tide extreme (approximately ±2.7 days) is tested statistically. The distribution of the time difference between the predicted and occurred events has a Gauss fit with adjusted R-square approximately equal to 0.89 and w = 4.2 ± 0.6.
This result can be interpreted like reliable approach for solving the “when” regional imminent seismic activity problem.
The discrepancy between values of Gauss fit parameter w for different cases is probably connected with INTERMAGNET one-minute samples.
Acknowledgements
The results presented in this paper rely on the data collected at INTERMAGNET PAG (Panagjurishte, Bulgaria), SUA (Surlari, Romania), AQU (L’Aquila, Italy) stations. We thank the Geophysical Institute of the Bulgarian
Figure 5. Day difference distribution for AQU (L’Aquila Italy) data and its Gauss fit.
Academy of Science for supporting PAG operation and INTERMAGNET for promoting high standards of magnetic observatory practice (www.intermagnet.org).
The financial support in the framework of FP7, Marie Curie Actions, International Research Staff Exchange Scheme, Project title: Complex Research of Earthquake’s Forecasting Possibilities, Seismicity and Climate Change Correlations, Acronym: BlackSeaHazNet, Grant Agreement Number: PIRSES-GA-2009-246874 as well the support of INRNE, BAS, are highly appreciated.
We would like to thank heartily the REA project officers heartily Dr. Oscar Perez-Punzano and Dr. Atantza Uriarte-Iraola, for their invaluable support in the process of negotiation and executing the project as well as to express our sincere gratitude to the DG Institute for Nuclear Research and Nuclear Energy, BAS in the face of Directore Assoc. Prof. Dr. Dimitar Tonev and Vice Director Assoc. Prof. Dr. Lachezar Georgiev, for the encouragement and valuable assistance, to Dr. Frank Marx, and in his face―to the European Commission, for the financial support for the BlackSeaHazNet project realization.
We would like to note the technical help of RadkaMavrodieva and DimitarHaydutov.
Conflict of Interest
The authors declare that they have no conflict of interest.
Cite this paper
Strachimir Cht.Mavrodiev,LazoPekevski,GiorgiKikuashvili,EmilBotev,PetarGetsov,GaroMardirossian,GeorgiSotirov,DimitarTeodossiev, (2015) On the Imminent Regional Seismic Activity Forecasting Using INTERMAGNET and Sun-Moon Tide Code Data. Open Journal of Earthquake Research,04,102-113. doi: 10.4236/ojer.2015.43010
References
- 1. Aki, K. (1995) Earthquake Prediction, Societal Implications. Reviews of Geophysics, 33, 243-247. http://dx.doi.org/10.1029/95RG00396
- 2. Main, I. (1999a) Is the Reliable Prediction of Individual Earthquakes a Realistic Scientific Goal? Debate in Nature. http://www.nature.com/ nature/ /earthquake/equake contents.html
- 3. Main, I. (1999b) Earthquake Prediction: Concluding Remarks. Nature Debates, Week 7.
- 4. Ludwin, R.S. (2001) Earthquake Prediction. Washington Geology, 28, 27, Debates.
- 5. Pakiser, L. and Shedlock, K.M. (1995) Predicting Earthquakes. USGS. http://earthquake.usgs.gov/hazards/prediction.html
- 6. Geller, R.J., Jackson, D.D., Kagan, Y.Y. and Mulargia, F. (1997) Earthquakes Cannot Be Predicted. Science, 275, 1616. http://dx.doi.org/10.1126/science.275.5306.1616
- 7. Tamrazian, G.P. (1967) Tide-Forming Forces and Earthquakes. International Journal of the Solar System, 7, 59-65.
- 8. Knopoff, L. (1964) Earth Tides as a Triggering Mechanism for Earthquakes. Bulletin of the Seismological Society of America, 54, 1865-1870.
- 9. Ryabl, A., Van Wormer, J.D. and Jones, A.E. (1968) Triggering of Micro Earth-Quakes by Earth Tides and Other Features of the Truckee, California, Earthquake Sequence of September 1966. Bulletin of the Seismological Society of America, 58, 215-248.
- 10. Shlien, S. (1972) Earthquake—Tide Correlation. Geophysical Journal of the Royal Astronomical Society, 28, 27-34. http://dx.doi.org/10.1111/j.1365-246X.1972.tb06108.x
- 11. Molher, A.S. (1980) Earthquake/Earth Tide Correlation and Other Features of the Susanville, California, Earthquake Sequence of June-July 1976. Bulletin of the Seismological Society of America, 70, 1583-1593.
- 12. Sounau, M., Sounau, A. and Gagnepain, J. (1982) Modeling and Detecting Interaction between Earth Tides and Earthquakes with Application to an Aftershock Sequence in the Pyrenees. Bulletin of the Seismological Society of America, 72, 165-180.
- 13. Shirley, J. (1988) Lunar and Solar Periodicities of Large Earthquakes: Southern California and the Alaska Aleutian Islands Seismic Region. Geophysical Journal, 92, 403-420.
- 14. Bragin, Y.A., Bragin, O.A. and Bragin, V.Y. (1999) Reliability of Forecast and Lunar Hypothesis of Earthquakes. Proceedings of the XXII General Assembly of the International Union of Geodesy and Geophysics (IUGG), Birmingham, 18-30 July 1999.
- 15. Thanassoulas, C. (1999) An Integrated Methodology Answering on “Where”, “When” and “Of What Magnitude”, a Large EQ Will Occur. http://www.earthquakeprediction.gr/
- 16. Thanassoulas, C. and Klentos, V. (2001) Very Short-Term (±1 Day, ±1 h) Time-Prediction of a Large Imminent Ear- thquake, the Second Paper. Institute of Geology and Mineral Exploration (IGME), Athens, Greece. Open File Report: A, 4384, 1-24.
- 17. Thanassoulas, C. and Klentos, V. (2001) The “Energy-Flow Model” of the Earth’s Lithosphere, Its Application on the Prediction of the “Magnitude” of an Imminent Large Earthquake. The Third Paper, Institute of Geology and Mineral Exploration (IGME), Athens, Greece. Open File Report: A, 4384, 1-20.
- 18. Varotsos, P. and Alexopoulos, K. (1984) Physical Properties of the Variations of the Electric Field of the Earth Preceding Earthquakes, I. Tectonophysics, 110, 93-98. http://dx.doi.org/10.1016/0040-1951(84)90059-3
- 19. Varotsos, P. and Alexopoulos, K. (1984) Physical Properties of the Variations of the Electric Field of the Earth Preceding Earthquakes, II. Tectonophysics, 110, 99-125. http://dx.doi.org/10.1016/0040-1951(84)90060-X
- 20. Varotsos, P., Lazaridou, M., Eftaxias, K., Antonopoulos, G., Makris, J. and Kopanas, J. (1996) Short-Term Earthquake Prediction in Greece by Seismic Electric Signals. In: Ligthhill, S.J., Ed., A Critical Review of VAN: Earthquake Prediction from Seismic Electric Signals, World Scientific Publishing Co., Singapore, 29-76. http://dx.doi.org/10.1142/9789812815491_0002
- 21. Hayakawa, M. and Fujinawa, Y. (1994) Electromagnetic Phenomena Related to Earthquake Prediction, Terrapub, Tokyo, 677.
- 22. Hayakawa, M., Fujinawa, Y., Evison, F.F., Shapiro, V.A., Varotsos, P., Fraser-Smith, A.C., Molchanov, O.A., Pokhotelov, O.A., Enomoto, Y. and Schloessin, H.H. (1994) What Is the Future Direction of Investigation on Electromagnetic Phenomena Related to Earthquake Prediction? In: Hayakawa, M. and Fujinawa, Y., Eds., Electromagnetic Phenomena Related to Earthquake Prediction, Terrapub, Tokyo, 667-677.
- 23. Hayakawa, M. (1999) Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes. Terrapub, Tokyo, 996.
- 24. Hayakawa, M., Ito, T. and Smirnova, N. (1999) Fractal Analysis of ULF Geomagnetic Data Associated with the Guam Earthquake on 8 August 1993. Geophysical Research Letters, 26, 2797-2800. http://dx.doi.org/10.1029/1999GL005367
- 25. Hayakawa, M., Itoh, T., Hattori, K. and Yumoto, K. (2000) ULF Electromagnetic Precursors for an Earthquake at Biak, Indonesia on 17 February 1996. Geophysical Research Letters, 27, 1531-1534. http://dx.doi.org/10.1029/1999GL005432
- 26. Hayakawa, M. and Molchanov, O. (2002) Seismo Electromagnetics Lithosphere-Atmosphere-Ionosphere Coupling. Terrapub, Tokyo, 477.
- 27. Oike, K. and Ogawa, T. (1982) Observations of Electromagnetic Radiation Related with the Occurrence of Earthquake. Annual Report Disaster Prevention Research Institute of Kyoto University, 25, 89-100.
- 28. Oike, K. and Yamada, T. (1994) Relationship between Shallow Earthquakes and Electromagnetic Noises in the LF and VLF Ranges. In: Hayakawa, M. and Fujinawa, Y., Eds., Electromagnetic Phenomena Related to Earthquake Prediction, Terrapub, Tokyo, 115-130.
- 29. Saraev, A.K., Pertel, M.I. and Malkin, Z.M. (2002) Correction of the Electromagnetic Monitoring Data for Tidal Variations of Apparent Resistivity. Journal of Applied Geophysics, 49, 91-100. http://dx.doi.org/10.1016/S0926-9851(01)00101-X
- 30. Eftaxias, K., Kapiris, P., Polygiannakis, J., Bogris, N., Kopanas, J., Antonopoulos, G., Peratzakis, A. and Hadjicontis, V. (2001) Signature of Pending Earthquake from Electromagnetic Anomalies. Geophysical Research Letters, 28, 3321- 3324. http://dx.doi.org/10.1029/2001GL013124
- 31. Eftaxias, K., Kapiris, P., Dologlou, E., Kopanas, J., Bogris, N., Antonopoulos, G., Peratzakis, A. and Hadjicontis, V. (2002) EM Anomalies before the Kozani Earthquake: A Study of Their Behavior through Laboratory Experiments. Geophysical Research Letters, 29, 69-1-69-4. http://dx.doi.org/10.1029/2001gl013786
- 32. Thanassoulas, C. (1991) Determination of the Epicentral Area of Three Earthquakes (Ms > 6R) in Greece, Based on Electrotelluric Currents Recorded by the VAN Network. Acta Geophysica Polonica, 4, 373-387.
- 33. Thanassoulas, C., Tsatsaragos, J. and Klentos, V. (2001) Determination of the Most Probable Time of Occurrence of a Large Earthquake. Open File Report A. 4338, IGME, Athens.
- 34. Ustundag, B. (2001) Earthquake Forecast. Data Acquisition and Evaluation Page. http://www.deprem.cs.itu.edu.tr/
- 35. Dean, R. (2003) http://www.earthquakeforecast.org
- 36. Contadakis, M., Biagi, P. and Zschau, J. (2002) Seismic Hazard Evaluation, Precursory Phenomena and Reliability of Prediction. Proceedings of the 27th EGS General Assembly, Nice, 21-26 April 2002.
- 37. Papadopoulos, G. (2003) 1st International Workshop on Earthquake Prediction Sub Commission on Earthquake Prediction Studies (SCE) of the European Seismological Commission Scheduled, Athens.
- 38. Zhonghao, S. (1999) Earthquake Clouds and Short Term Prediction.
- 39. Silina, A.S., Liperovskaya, E.V., Liperovsky, V.A. and Meister, C.V. (2001) Ionospheric Phenomena before Strong Earthquakes. Natural Hazards and Earth System Sciences, 1, 113-118. http://dx.doi.org/10.5194/nhess-1-113-2001
- 40. Larkina, V.I. and Ruzhin, Y.Y. (2003) Wave Satellite Monitoring of Earthquake Precursors in the Earth Plasmasphere. 1st International Workshop on Earthquake Prediction, Sub Commission on Earthquake Prediction Studies (SCE) of the European Seismological Commission Scheduled, Athens, Greece. http://www.gein.noa.gr/services/Workshop.htm
- 41. Mavrodiev, S.C. and Thanassoulas, C. (2001) Possible Correlation between Electromagnetic Earth Fields and Future Earthquakes. Seminar Proceedings, Sofia, 23-27 July 2001, 41. http://arXiv.org/abs/physics/0110012
- 42. Mavrodiev, S.C. (1998) Applied Ecology of the Black Sea. Nova Science Publishers, Inc., New York, 207 P.
- 43. Mavrodiev, S.C. (2002) The Electromagnetic Fields under, on and up Earth Surface as Earthquakes Precursor in the Balkans and Black Sea Regions. Physics, Subj-Class: Geophysics; Atmospheric and Oceanic Physics.
- 44. Mavrodiev, S.C. (2002) On the Short Time Prediction of Earthquakes in Balkan-Black Sea Region Based on Geomagnetic Field Measurements and Tide Gravitational Potential Behaviour. http://arXiv.org/abs/physics/0210080
- 45. Mavrodiev, S.C. (2003) The Electromagnetic Fields under, on and Earth Surface as “When, Where and How” Earthquake Precursor, Workshop on Gujarat Earthquake, Kanpur, India. http://www.arxiv.org/ftp/physics/papers/0302/0302033.pdf
- 46. Mavrodiev, S.C. (2003) The Electromagnetic Fields under, on and over Earth Surface as “When, Where and How” Earthquake Precursor, European Geophysical Society, Geophysical Research Abstracts, 5, 04049.
- 47. Mavrodiev, S.C. (2004) On the Reliability of the Geomagnetic Quake as a Short Time Earthquake’s Precursor for the Sofia Region. Natural Hazards and Earth System Sciences, 4, 433-447.
- 48. Mavrodiev, S.C. and Pekevski, L. (2008) Complex Regional Network for Earthquake Researching and Imminent Prediction. Electromagnetic Phenomena Related to Earthquakes and Volcanoes. Birbal Singh, Publ., Narosa Pub. House, New Delhi, 135-146.
- 49. Dierks, O. and Neumeyer, J. (2002) Comparison of Earth Tides Analysis Programs. Geo Forschungs Zentrum Potsdam, Division 1, Telegrafenberg, Potsdam, 14473.
- 50. Wenzel, H.G. (1996) Thenanogal Software: Earth Tide Data Processing Package ETERNA 3.30. In: Melchior, P., Ed., Marees Terrestres Bulletin Informations, Vol., 124, Association Internationale de G′eod′esie, Bruxelles, 9425-9439.
- 51. Wenzel, H.-G. (1996b) ETERNA Manual. Version 3.30, Black Forest Observatory, Karlsruhe.
- 52. Tamura, Y., Sato, T., Ooe, M. and Ishiguro, M. (1991) A Procedure for Tidal Analysis with a Bayesian Information Criterion. Geophysical Journal International, 104, 507-516. http://dx.doi.org/10.1111/j.1365-246X.1991.tb05697.x
- 53. Venedikov, A. and Arnoso, R. (2001) Program VAV/2000 for Tidal Analysis of Unevenly Spaced Data with Irregular Drift and Colored Noise. Journal of Geodetic Society of Japan, 47, 281-286.
- 54. Venedikov, A.P., Arnoso, R. and Vieira, R. (2003) A program for Tidal Data Processing. Computer & Geoscience’s, 29, 487-502. http://dx.doi.org/10.1016/S0098-3004(03)00019-0
- 55. Balsh, C. (2003) http://www.sel.noaa.gov/info/Kindex.html
- 56. Mavrodiev, S.C., Pekevski, L. and Jimseladze T. (2008) Geomagnetic-Quake as Imminent Reliable Earthquake’s Precursor: Starting Point for Future Complex Regional Network. Electromagnetic Phenomena Related to Earthquakes and Volcanoes. Narosa Pub. House, New Delhi, 116-134.
- 57. Mavrodiev, S.C., Pekevski, L. and Kikuashvili, G. (2013) Results of BlackSeaHazNet Project—FP7 IRSES Project: Extended Executive Summary, Conclusion Workshop, BlackSeaHazNet Series, Sofia, 3.
- 58. Mavrodiev, S.C., Kilifarska, N., Pekevski, L. and Kikuashvili, G. (2014) BlackSeaHazNet Scientific Report—EU FP7 IRSES Project 2011-2014. http://arxiv.org/ftp/arxiv/papers/1410/1410.6106.pdf
- 59. (2006) http://theo.inrne.bas.bg/~mavrodi/project.html
- 60. (2014) http://cordis.europa.eu/result/rcn/148955_en.html








