Open Journal of Earthquake Research
Vol.04 No.01(2015), Article ID:54188,13 pages
10.4236/ojer.2015.41003
Current State of Strain in the Central Cascadia Margin Derived from Changes in Distance between GPS Stations
Kenneth M. Cruikshank, Curt D. Peterson
Department of Geology, Portland State University, Portland, Oregon, USA
Email: CruikshankK@pdx.edu, PetersonC@pdx.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 January 2015; accepted 11 February 2015; published 17 February 2015
ABSTRACT
Using continuously operating Global Positioning Stations in the Pacific Northwest of the United States, over 100 station-station baseline length changes were determined along seven West-East transects, two North-South transects and in three localized areas to determine both the average annual strains over the past several years, and the variation in strain over the central Cascadia convergent margin. The North-South transects (composed of multiple baselines) show shortening. Along West-East transects some baselines show shortening and others extension. The direction of the principle strains calculated for two areas 100 km from the deformation front are close to perpendicular to the deformation front. The North-South strains are 10−8 a−1, which is an order-of- magnitude less than the West-East strains (10−7 a−1). Along several West-East transects, the magnitude of the strain increases away from the deformation front. All West-East transects showed a change in strain 250 km inland from deformation front.
Keywords:
Convergent Margin, Cascadia, Strain, Strain-Energy, GPS

1. Introduction
Paleoseismic work suggests that the United States Pacific Northwest (Figure 1) has episodic large earthquakes, and is currently in an interseismic period [1] [2] when we would expect strain to be accumulating between the descending Juan de Fuca plate to the west and the overriding North American Plate to the east (Figure 1). The central Cascadia margin (Oregon and Washington) was chosen for this study of modern strain accumulation because 1) it represents a relatively uniform section of a shallow dipping (5˚ - 12˚) megathrust system [3] and
Figure 1. Location of the study area in the Pacific Northwest region of the United States (County lines are in Oregon and Washington are shown for reference). The tectonic provinces discussed in this paper are the Coastal Range (Coast Range and Olympic Peninsula), Fore-arc basin (Puget/Willamette lowlands), and the volcanic Cascade Mountains. The locations of major volcanic centers are marked with triangles. The Cascadia subduction zone deformation front is at the Western extent of the traces of faults and fold axis shown offshore of Oregon and Washington [11] . Current plate convergence is NE- SW (shown by large arrows).
2) it includes a dense network (40 - 50 km spacing) of continuously operating Global Positioning System (GPS) stations [4] [5] . This article includes more details of methodology and strain analysis than preceding articles [6] -[8] that have demonstrated active strain accumulation in the landward positions of the subduction zone.
The energy released during an earthquake comes from stored elastic energy (strain-energy) in the Earth’s crust [9] . GPS Strain measurements following the 2011 Tōhoku earthquake demonstrated that the distribution of strain is not uniform in some subduction zones [10] . Understanding the variation in strain during a preceding interseismic cycle is important in prediction of the distribution of energy release during an earthquake. Strain is fundamental to evaluating the stored elastic strain energy in the Earth’s crust. These patterns in strain are helpful in evaluating various kinematic and mechanical models of crustal deformation. Good quantitative and qualitative understandings of the magnitudes and patterns of strain are important in describing the deformation of a coseismic region. A summary of the GPS Research in the Pacific Northwest is provided in [11] .
In this paper we use a fundamental approach to determine strain; for a single baseline we use the change in length of the vector between fixed GPS stations. This avoids issues that are introduced by the removal of rigid- body motions, as required in deriving strains from GPS velocities, thus giving a more direct picture of strain in the Cascadia Subduction zone (Figure 1). In this paper we document present changes in baseline distances between a series of fixed, continuously operating GPS stations along seven West-East transects and two North- South transects in the central Cascadia margin. We also present principle strain magnitudes and directions at three locations based on measurements in braced quadrilaterals. These results give a general picture of the pattern of strain accumulation in the Pacific Northwest over the past five to seven years which raises some important questions about the mechanisms that are generating the measured strain.
2. Methods
Strain is defined as the change in distance between the two material points [12] [13] . The fundamental differentially-corrected GPS solution gives the vector between the phase centers of two GPS antenna [14] [15] . Changes in the vector length over a given period give an accurate measure of strain, without having to consider additional uncertainties typically involved when using station displacement vectors, or in deriving station velocities in some arbitrary coordinate system [16] . It should be noted that whatever uncertainties are present in the baseline determination are also present in other solutions based on variation of coordinates. The main difference between GPS station-to-station strain (used here) and strain from GPS derived station velocities is how rigid body motion, particularly rotation, is handled.
Strain, ε, is defined as the normalized change in length of a line between two material points
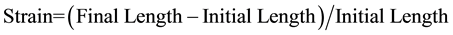 (1)
(1)
Strain, ε, will be negative if the distance between two points gets shorter (shortening), positive if the distance increases (extension), and zero if it is unchanged.
In two-dimensions strain is usually described with two principle components [13] . If the principle components and their direction are known then the strain can be described for any arbitrary orientation Equation (2). However, strain is a three-dimensional problem, and so if represented by an ellipsoid with three principal axes. In measuring geodetic strain, an ellipse which is a horizontal section through the three-dimensional ellipsoid is determined. These major and minor axies of the ellipse are not necessarily the true principle components; however, they do help in describing the general state of strain in the crust and can be viewed as two-dimensional surrogates for the principle strains.
The strain, l, in a direction ε to the greatest strain (Figure 2) is given by:
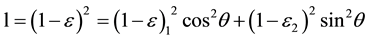 (2).
(2).
Using Equation (2) the major (ε1) and minor (ε2) axis of the ellipse can be solved, given several strains (ε) in different directions (θ).
Figure 2. (a) A circle prior to any deformation is transformed into an ellipse during deformation. All radii of the circle were originally the same length. One of the radii will become the major axis of the ellipse, and a radius perpendicular to that would become the minor axis; (b) The length of any arbitrary line, l will be a function of the length of the major and minor axis, which represent the maximum (ε1) and minimum strains (ε2) (the principle strains), and the orientation of the line relative to the major axis (θ).
2.1. Baseline Length Determination
From the fixed GPS network in the Pacific Northwest (Oregon and Washington, see Figure 3) a series of West- East transects was selected to give strain profiles lines that extended from the coastline to the Cascade Mountains.
Daily RINEX files from Pacific Northwest Geodetic Array [5] and NOAA Continually Operating Reference stations [4] , along with the precise ephemeris files from the International GPS Service (IGS) [17] are processed with vecsol, [18] , which is part of the GPSTK toolkit [19] . Vecsol solves for the baseline vector between two stations. During processing, one station is designated as the start of the vector, and the other as the end. The baselines are processed twice, using each end as the starting point of the vector and the other as the end point. The two baselines are compared for consistency. Typically, solutions are calculated for several years to look for the long term trends in changes in the baseline. At least two years of data are needed to ensure the trend is not influenced by annual variations in baseline lengths [20] . The baseline vectors are stored in a database and analyzed using R [21] . Scatter plots are examined for outliers. Sometimes, due to a GPS solution that failed to converge, the data are not discarded but flagged in the database as problematical. To look for a trend in the data, the R function rlm (part of the MASS package) is used; this regression includes the ability to minimize the effect of outliers. If a significant trend is found in the data (as determined by the t-and F-test results generated by rlm), the slope of the line is expressed as the average change of length per year. This is converted to a strain to calculate the average strain per year. An example of baselines is shown in Figure 4. The plots show the variation in baseline lengths for two representative lines. Variations in baseline length between stations ARLN (Arlington,
Figure 3. Map showing global positioning system fixed reference stations in the pacific northwest, strain transects, and strain ellipses presented in this paper.
Figure 4. Plots showing the variation in baseline lengths and the best-fit trend for two representative lines. The horizontal axis is time, and the vertical axis is distance (in meters), with decimeter divisions. (a) Variations in baseline length between stations ARLN (Arlington, Oregon) and P445 (Wasco Airport, Oregon) from 2008 to 2014; (b) Variations in baseline length between stations P402 (near Forks, Washington) and P403 (Sappho, Washington) from 2008 to 2012. Station Positions are shown in Figure 3.
Oregon) and P445 (Wasco Airport, Oregon) are from 2008 to 2014. There are 3274 baseline lengths used in the regression. The baseline length is 40.3 km, and the regression indicates the baseline is getting shorter by 4.28 mm per year, which is an average strain of −1.14 × 10−7 each year in an almost West-East direction (the direction from ARLN to P445 is 251˚, or 19˚ South of West). The variation in baseline length between stations P402 (near Forks, Washington) and P403 (Sappho, Washington) from 2008 to 2012. There are 2764 baseline lengths used in the regression. The baseline length is 35.1 km, and the regression shows the baseline is getting shorter by 5.2 mm per year, which is an average strain of −1.47 × 10−7 each year in nearly a North-South direction (the direction from P402 to P403 is 20˚, or 20˚ East of North). Station Positions are shown in Figure 3.
Because strain is the change in distance between to material points, it describes the average strain in the material between the two material points. It is possible that strain could be non-uniform in the interval between two GPS stations. The test for significance of regression is that the slope of the best-fit line is significantly different from a horizontal line [22] , therefore a smaller strain magnitude would indicate a less significant trend. Some of the “Not significant” lines in Table 1 could represent areas of little or no strain.
2.2. Strain Ellipse Determination
In selected areas, baseline strains were used to compute the best-fit strain ellipsoid over an area (Figure 2). Just as the strain measurements are an average of the change in distance between two points, the strain ellipse represents an average strain over the area covered by the lines. A series of stations forming a braced quadrilateral were used [23] . The directions of lines between stations were computed using the Vincenty method [24] .
In obtaining a solution a direction for the major axis of the ellipse is assumed and then the magnitude of the axes is solved for using least squares. From these solutions the predicted strains are computed for a baseline using its orientation (Equation (2)). The predicted strains are then compared with the observed strains and a sum of the differences (the residual) is computed. The best orientation of the major axis and strain corresponding magnitudes is the solution that minimizes the residuals. This is the best fit strain (Figure 2).
3. Results
Our results are presented in Tables 1-3, and in Figure 5. There strains are computed for 81 baselines along 9 transects with 166,300 individual baseline computations. For the three strain ellipses 26 baselines were used, with 39,000 individual baselines length calculations. The data records cover the period from 2006 to 2014
Table 1. Station ID, locations, and range of dates used in obtaining the strains.
(Tables 1-3). Not all stations were active for this entire period.
The distances between many of the GPS stations are on the order of 40 km (Figure 3). Strain over shorter distances cannot be resolved. The spatial variations in strain are probably accurate at a scale of 80 km. This is treating resolution as being limited by the Nyquist frequency based on the data spacing [25] . The distances in all of the plots have been adjusted to be 0 km at the western (offshore) extent of the deformation front (Figure 1). The granularity in the strain measurements require that strain analyses and interpretations are conducted at the regional scale rather than for discrete (tens of kilometer scale) faults or folds.
3.1. Transects
The West-East lines indicate that strain varies in magnitude changing from shortening to extension between the coast and the Cascade Mountains (Table 2 and Figure 5(a)). The two north-south lines show relatively uniform shortening (Table 4 and Figure 5(b)), although, it is on average an order of magnitude less than strains along West-East transects (10−8 a−1 for N-S, with many W-E strains being 10−7 a−1).
3.2. West-East Transects Descriptions (North to South)
In some transects there were insufficient data to establish a significant baseline. These baselines are identified in Tables 1-3. They show up as gaps along transects in Figure 5(a).
There are 9 baselines in the Northern Olympic transect. The measured strains range from −5.47 × 10−7 a−1 to +1.33 × 10−7 a−1. Two baselines did not contain sufficient data for a trend. Some baselines near the coast show extension while other baselines show and a small amount of shortening (Table 1). At 250 km distance landward from the deformation front the strains increase and become all shortening. There are 6 baselines in the Tacoma transect. The measured strains range from −1.39 × 10−7 a−1 to +2.79 × 10−7 a−1. Two baselines did not contain sufficient data for a trend. The strains nearest the coast are extension; further inland the strain magnitudes become smaller, and at 250 km from the deformation front they indicate a small magnitude of shortening. There are 8 baselines in the Olympia transect. The measured strains range from −9.71 × 10−8 a−1 to +2.75 × 10−7 a−1. Two baselines did not contain sufficient data for a trend. Baselines nearest the coast show shortening, but 235 km from the deformation front baselines show extension, while baselines further inland show shortening. There are 7 baselines in the Willipa Bay transect. The measured strains range from −1.98 × 10−7 a−1 to −4.76 × 10−8 a−1.
Table 2. Data for North-South Lines, similar to that in Table 1.
Two baselines did not contain sufficient data for a trend. All the strains along this transect show shortening. The amount of shortening decreases inland from the coast.
There are 9 baselines in the Portland transect. The measured strains range from −2.68 × 10−7 a−1 to −2.56 × 10−9 a−1. One baseline did not contain sufficient data for a trend, and one was not a significant trend (Table 1). The individual baseline strains along this transect are all shortening. The greatest amount of shortening occurs at 350 to 400 km from the deformation front. There are 7 baselines in the Newport transect. The measured strains range from −1.98 × 10−7 a−1 to −4.76 × 10−8 a−1. The baseline strains nearest the deformation front are shortening, but the baselines show extension 250 km from the deformation front. In the Cape Blanco transect, there are 97 baselines. The measured strains range from −1.79 × 10−7 to + 5.11 × 10−8. Three baselines did not give a significant trend. The strains near the deformation front are shortening, and the amount of shortening increases to the
Table 3. Data used for the strain ellipsoid determinations.
east until 250 km from the deformation front, where they decrease in magnitude showing a small amount of extension.
There are 9 baselines in the Coast Range North-South transect (Table 2). The measured strains range from −2.20 × 10−7 a−1 to −2.16 × 10−8 a−1. Two baselines did not give a significant trend. The strains are shortening, with the magnitude generally decreasing to the south. There are 18 baselines in the East of Cascades transect. The measured strains range from −1.11 × 10−7 a−1 to +1.98 × 10−7 a−1. Two baselines did not contain sufficient data for a trend. The strains are shortening, with less variation than the Coast Range transect. Within transects, most of the variability is in the south.
Overall West-East lines show that strain varies in magnitude, and changes from shortening to extension between the coast and the Cascade Mountains (Table 2 and Figure 5(a)). The two north-south lines show relatively uniform shortening (Table 4 and Figure 5(b)), although it is on average an order of magnitude less than
Table 4. Principle strain directions and magnitudes. Both principle strains are shortening. Locations of the stations used for those strains are shown in Figure 3.
Figure 5. Changes in strain along GPS station transects. All West-East transects are to the same scale, the North-South transects are an expanded scale show variation. The reader should refer to Table 1 and Table 2 for actual strain values. (a) Changes in strain along W-E transects. Top of plot is North, bottom is South. The horizontal gridlines for any transect represents zero strain. Line segments above a reference line represents extension (positive strain), and segments below the line represent shortening (negative strain); (b) Changes of strain along N-S transects. Line on left is along Coast Range, and the line on the right is to the east of the Cascade Mountains, 300 km east of the Coast Range Line. The vertical reference lines represent zero strain. Line segments to the right of a reference line represents extension (positive strain), and segments left of the reference line represent shortening (negative strain).
strains that are seen West-East (10−8 a−1 for N-S, with many W-E strains being 10−7 a−1).
The more northerly transects show extension near the coast with shortening further inland, whereas the more southerly transects show the largest amount of shortening nearest the deformation front, with decreasing strain to the east. Some of the more easterly strains on the Oregon transects show extension.
3.3. Strain Ellipse Results
Strains were computed for three ellipses. The Northernmost ellipse is in the Northwest of the Olympic Peninsula (Figure 3 and Table 3). Eight baselines were used to calculate the ellipse. A second ellipse, the Vernonia ellipse, is in the Coast Range in Northern Oregon. Here, 12 baselines were used to determine the best-fit ellipse. The third ellipse is located in Southeast Oregon. Six baselines were used to compute the best-fit ellipse.
The West-East transects show shortening the Coast Range. In the North-South transects there is also shortening (although an order of magnitude less than West-East). This result also shows in the strain ellipse results (Table 4), where both major axis of the ellipse represent shortening, with the maximum shortening oriented ENE-WSW. The fact that both major axis are shortening would suggest that the material being deformed may be reducing in volume, or thickening or that the computed ellipse is an oblique view of the actual three-dimensional strain ellipse. The dominant strain is West-East as expected in a convergent margin and measured strain is found to extend 450 km inland from the deformation front in the study area.
The principle strain directions in the Vernonia and Olympics ellipses are different by 30˚ with the Vernonia principle shortening orientation being clockwise relative to the NW Olympic Peninsula. The orientation of the deformation front rotates at least 15˚ in this area (Figure 1). Therefore the trend in the principle strain orientations remains close to perpendicular to the deformation front. In general the direction of maximum shortening is perpendicular to the margin as expected in a convergent margin.
The SE Oregon ellipse is located NW of Burns Junction which is 450 km landward of the Cascade margin (Figure 1). Here the ellipse is not as well defined as those computed for the Coast Range. The principle strains are closer in magnitude and they are an order of magnitude less than those of the Coast Range. West-East strains decline substantially east of the Cascades volcanic arc.
4. Discussion
The coastal strain ellipses indicate that the direction of maximum shortening is generally perpendicular to the deformation front, as expected. However, the West-East transects are not as straightforward as one might imagine; it is generally assumed that there would more widespread West-East shortening with the amount of strain decreasing to the East. This behavior is only seen in the four Oregon transects. The northern two transects show extension nearest the coast with shortening further inland.
The North-South and West-East transects and the strain ellipse solutions all document both North-South and West-East shortening. Previous studies in the northern Cascadia forearc [26] have documented North-South shortening. The stresses in the Pacific Northwest show the principle stress direction being roughly North-South [27] -[29] . This study shows the principle strain direction to be roughly West-East. It is unclear how these results reconcile, but the North-South maximum stress may help explain the North-South shortening that is measured. It is expected that the West-East principle stress would also be compressive, but it is unclear why the lesser of the two stresses results in the greater strain.
From a hazards perspective, the strains are important because they give insights into the spatial variation of strain energy accumulation. A suitable surrogate for looking at patterns of accumulating strain energy are the absolute values of the strains. Following linear elastic mechanics the stored energy is proportional to the strain. Once the principle strains (ε1, ε2, ε3) are known, the elastic strain energy is given by [30] :
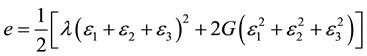 (3a)
(3a)
where G and λ are material parameters that are a function of Poisson’s Ratio (ν) and Young’s modulus (E):
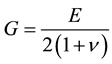 and (3b)
and (3b)
The strains in the energy equation are all squared, so the values of the squares will be positive numbers. The energy is proportional to the square of the absolute value of the strains, which are shown in Figure 6.
There is no way of knowing if an area of extension, for example, is increasing its stored energy or losing it to relaxation. The same is true for areas under shortening. Which will only become apparent when the interseismic strain is compared to change in strains in an actual earthquake. For example, if Episodic Tremor Slip (ETS) [31] events are releasing stored energy, it is expected that the strains during an ETS event will be the opposite of the long-term interseismic change in strain. Such ETS events might only represent the transfer of stored elastic strain from one area to another.
The Northern Olympics transect shows that the stored energy is increasing away from the deformation front. It reaches a maximum at 250 km from the deformation front. The Tacoma transect shows the opposite with the amount of stored energy decreasing from the coast. The energy of the Olympic Transect is at a maximum at 250 - 300 km from the deformation front. The stored elastic energy decreases from the coast as demonstrated by strains along the Willipa Bay, Portland, and Newport transects. The Willipa Bay and Portland Transects show an increase in stored energy 250 km from the deformation front on the east side of the forearc valley (Willamette Valley). The Cape Blanco transect is more similar to the Northern Olympic transect in that it shows an increase
Figure 6. Absolute value of the strain (strain magnitude). Strain energy is proportional to the absolute value of strain. The lines represent the magnitude of strain energy accumulation along the transects. These plots are similar to Figure 5, and the data are from Table 1 and Table 2. The same scale is used for all West-East transects. A constant, but different, scale is used for all the North- South transects.
in strain energy up to 250 km from the deformation front. Due to a lack of GPS stations located in the Pacific Ocean between the coast and the deformation front (Figure 1) the modern strains accumulating in the strongly coupled zone [8] are not established.
5. Conclusions
The value of the description of the strain presented here is that it gives observations against which models of the landward part of the Cascadia zone, including the transition zone, can be compared. Models should be able to generate “expected” strains which can now be compared against observed strain patterns. A model that relies on dislocation fit solutions should be able to account for the observed distribution of strain. The strain distribution provides constraints for models (e.g., how far inland does the locked zone extend in a dislocation model). These short-term strains can also tie in with longer term strain indicators, such as uplift of the Coast Range, uplift of the western flank of the Cascades, and neotectonic features.
West-East GPS transects of station-station baselines show both shortening and extension along the same transects. The direction of principle shortening near the coast, as determined at two sites, is generally perpendicular to the deformation front. North-South transects show shortening strains along the length of the study area. Most West-East Transects show an increase in strain 250 km from the deformation front which represents the Western flank of the Cascades. Many West-East Transects show a decrease in strain energy from 300 to 550 km east of the deformation front. The pattern of strains along transects are spatially variable, possibly indicating important asperities within the transition zone.
References
- Atwater, B.F. (1987) Evidence for Great Holocene Earthquakes along the Outer Coast of Washington State (USA). Science, 236, 942-944. http://dx.doi.org/10.1126/science.236.4804.942
- Darienzo, M.E. and Peterson, C.D. (1990) Episodic Tectonic Subsidence of Late Holocene Salt Marshes, Northern Oregon Central Cascadia Margin. Tectonics, 9, 1-22. http://dx.doi.org/10.1029/TC009i001p00001
- Parsons, T., Blakely, R.J., Brocher, T.M., Christensen, N.I., Fisher, M.A., Flueh, E., Kilbride, F., Luetgert, J.H., Miller, K., ten Brink, U.S., Trehu, A.M. and Wells, R.E. (2005) Crustal Structure of the Cascadia Fore Arc of Washington, United States Geological Survey, P-1661-D.
- CORS (2014) RINEX Data Files for NOAA CORS Stations. http://geodesy.noaa.gov/CORS/
- PANGA (2014) RINEX Files for GPS Stations in Pacific Northwest Geodetic Array. http://www.geodesy.cwu.edu/
- McCaffrey, R., Long, M.D., Goldfinger, C., Zwick, P.C., Nabelek, J.L., Johnson, C.K. and Smith, C. (2000) Rotation and Plate Locking at the Southern Cascadia Subduction Zone. Geophysical Research Letters, 27, 3117-3120. http://dx.doi.org/10.1029/2000GL011768
- Peterson, C.D. and Cruikshank, K.M. (2014) Quaternary Tectonic Deformation, Holocene Paleoseismicity, and Modern Strain in the Unusually-Wide Coupled Zone of the Central Cascadia Margin, Washington and Oregon, USA and British Columbia, Canada. Journal of Geography and Geology, 6, 33. http://dx.doi.org/10.5539/jgg.v6n3p1
- Peterson, C.D., Cruikshank, K.M. and Darienzo, M. (2014), Coastal Tectonic Strain and Paeloseismicity in the South Central Cascadia Margin, Oregon, USA. In: Vidovic, M., Ed., Earthquakes: Triggers, Environmental Impact and Potential Hazards, NOVA Open Access Publisher, Hauppauge.
- Reid, H.F. (1908) The California Earthquake of April 18, 1906: The Mechanics of the Earthquake. Vol. 2, The Carnegie Institution of Washington, Washington, D.C.
- Cruikshank, K.M. and Peterson, C.D. (2013) Strain Energy Release from the 2011 9.0 Mw Tōhoku Earthquake, Japan. Open Journal of Earthquake Research, 2, 75-83. http://dx.doi.org/10.4236/ojer.2013.24008
- McCaffrey, R., King, R.W., Payne, S.J. and Lancaster, M. (2013) Active Tectonics of Northwestern US Inferred from GPS-Derived Surface Velocities. Journal of Geophysical Research, 118, 709-723.
- Active Tectonics and Seafloor Mapping Lab (2014) Cascadia Neotetonic Map. Oregon State University. http://activetectonics.oce.orst.edu/casc_structure.htm
- Fung, Y.C. (1965) Foundations of Solid Mechanics. Prentice-Hall, Englewood Cliffs.
- Malvern, L.E. (1969) Introduction to the Mechanics of Continuous Medium. Prentice-Hall, Inc., Englewood Cliffs.
- Strang, G. and Borre, K. (1997) Linear Algebra, Geodesy, and GPS. Wellesley Press, Cambridge.
- Borre, K. and Strang, G. (2012) Algorithms for Global Positioning. Wellesley Cambridge Press, Cambridge.
- Torge, W. (2001) Satellite Geodesy. Walter de Gruyter, Berlin.
- International GPS Service (2014) Final Orbit Ephemeris.
- Vermeer, M. (2006) Geodetic Baseline GPS Processing by a Simple Sequential Technique. ION GNSS 19th International Technical Meeting of the Satellite Division, Fort Worth, 26-29 September 2006, 2977-2882.
- Tolman, B., Harris, R.B., Gaussiran, T., Munton, D., Little, J., Mach, R., Nelsen, S., Renfro, B. and Schlossberg, D. (2004) The GPS Toolkit―Open Source GPS Software. Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2004), Long Beach, 24 September 2004, 9 p.
- Blewitt, G. and Lavallée, D. (2002) Effect of Annual Signals on Geodetic Velocity. Journal of Geophysical Research, 107, ETG 9-1-ETG 9-11. http://dx.doi.org/10.1029/2001JB000570
- R Development Core Team (2008) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
- Davis, J.C. (2002) Statistics and Data Analysis in Geology. 3rd Edition, John Wiley & Sons, New York.
- Baum, R.L., Johnson, A.M. and Fleming, R.W. (1988) Measurement of Slope Deformation Using Quadrilaterals. United States Geological Survey. 23 p.
- Vincenty, T. (1975) Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations. Survey Review, 23, 88-93. http://dx.doi.org/10.1179/sre.1975.23.176.88
- Smith, S.W. (1997) The Scientist and Engineer’s Guide to Digital Signal Processing. California Technical Publication, San Diego, 628 p.
- Mazzotti, S., Dragert, H., Hyndman, R.D., Miller, M.H. and Henton, J.A. (2002) GPS Deformation in a Region of High Crustal Seismicity: N. Cascadia Forearc. Earth and Planetary Science Letters, 198, 41-48. http://dx.doi.org/10.1016/S0012-821X(02)00520-4
- Zoback, M. and Zoback, M. (1980) State of Stress in the Conterminous United States. Journal of Geophysical Research, 85, 6113-6155. http://dx.doi.org/10.1029/JB085iB11p06113
- Balfour, N.J. (2011) Sources of Seismic Hazard in British Columbia: What Controls Earthquakes in the Crust? University of Victoria, Victoria, 165 p.
- Balfour, N.J., Cassidy, J.F., Dosso, S.E. and Mazzotti, S. (2011) Mapping Crustal Stress and Strain in Southwest British Columbia. Journal of Geophysical Research, 116, 11 p.
- Jaeger, J.C., Cook, N.G.W. and Zimmerman, R.W. (2007) Fundamentals of Rock Mechanics. 4th Edition, Chapman and Hall, London.








