Open Journal of Earthquake Research
Vol.2 No.3(2013), Article ID:35778,15 pages DOI:10.4236/ojer.2013.23007
Control Parameters of Magnitude—Seismic Moment Correlation for the Crustal Earthquakes
Institute of Seismology of the National Academy of Sciences of the Kyrgyz Republic, Bishkek, Kyrgyz Republic
Email: nernesova@gmail.com; kis@elcat.kg
Copyright © 2013 Ernes Mamyrov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 12, 2013; revised July 19, 2013; accepted August 8, 2013
Keywords: Magnitude; Seismic Moment; Energy Class; Earthquakes; Frequency
ABSTRACT
In connection with conversion from energy class KR ( , where ER—seismic energy, J) to the universal magnitude estimation of the Tien Shan crustal earthquakes the development of the self-coordinated correlation of the magnitudes (mb, ML, Ms) and KR with the seismic moment M0 as the base scale became necessary. To this purpose, the first attempt to develop functional correlations in the magnitude—seismic moment system subject to the previous studies has been done. It is assumed that in the expression
, where ER—seismic energy, J) to the universal magnitude estimation of the Tien Shan crustal earthquakes the development of the self-coordinated correlation of the magnitudes (mb, ML, Ms) and KR with the seismic moment M0 as the base scale became necessary. To this purpose, the first attempt to develop functional correlations in the magnitude—seismic moment system subject to the previous studies has been done. It is assumed that in the expression , the coefficients ki and zi are controlled by the parameters of ratio
, the coefficients ki and zi are controlled by the parameters of ratio  (where
(where ; f0—corner frequency, Brune, 1970, 1971; M0, N×m). According to the new theoretical predictions common functional correlation of the advanced magnitudes Mm (mbm = mb, MLm = ML, MSm = MS) from log10M0, log10t0 and the elastic properties (Ci) can be presented as
; f0—corner frequency, Brune, 1970, 1971; M0, N×m). According to the new theoretical predictions common functional correlation of the advanced magnitudes Mm (mbm = mb, MLm = ML, MSm = MS) from log10M0, log10t0 and the elastic properties (Ci) can be presented as , where
, where , and
, and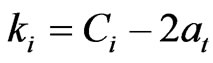 , for the averaged elastic properties of the Earth’s crust for the mbm the coefficients Ci = –11.30 and di = 1.0, for MLm: Ci = –14.12, di = 7/6; for MSm: Ci = –16.95 and di = 4/3. For the Tien Shan earthquakes (1960-2012 years) it was obtained that
, for the averaged elastic properties of the Earth’s crust for the mbm the coefficients Ci = –11.30 and di = 1.0, for MLm: Ci = –14.12, di = 7/6; for MSm: Ci = –16.95 and di = 4/3. For the Tien Shan earthquakes (1960-2012 years) it was obtained that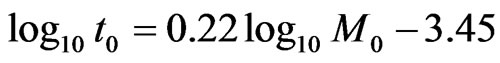 , and on the basis of the above expressions we received that MSm = 1.59mbm – 3.06. According to the instrumental data the correlation Ms = 1.57mb – 3.05 was determined. Some other examples of comparison of the calculated and observed magnitude—seismic moment ratios for earthquakes of California, the Kuril Islands, Japan, Sumatra and South America are presented.
, and on the basis of the above expressions we received that MSm = 1.59mbm – 3.06. According to the instrumental data the correlation Ms = 1.57mb – 3.05 was determined. Some other examples of comparison of the calculated and observed magnitude—seismic moment ratios for earthquakes of California, the Kuril Islands, Japan, Sumatra and South America are presented.
1. Introduction
In world practice, seismological research in assessing the scale of earthquakes magnitude scale of Gutenberg and Richter [1-3] is fundamental. In the countries of the former Soviet Union has been used scale independent energy class KR, defined as the logarithm of the seismic energy ER, highlighted by an earthquake, measured in joules (KR = log10ER, [4-6]).
For crustal earthquakes Tien Shan when considering the transition to magnitude scale was necessary to develop a self-consistent system of quantitative relationships that justify numerous empirical relationships bodywave magnitude mb, local magnitude on surface waves ML, surface wave magnitude for MS and KR from seismic moment M0 (N∙m), as the reference scale. In connection with the above purpose is to study the quantitative relationships mb, ML, MS and energy of seismic radiation ES c M0 based on the following findings:
1) proportional magnitudes and the maximum amplitude of seismic vibrations [1-3];
2) the statistical dependencies of the average magnitude of displacement along the fault u [7-12] and u functional relationship with the seismic moment, the shear modulus μ and the gap area S [13-14];
3) functional relationship corner period  with M0, the source radius r0, speed S—wave vS and static stress drop Δσ [15,16], as well as the similarity of the angular frequency f0 with a fundamental frequency of the acoustic Debye [17] fD, depending on the amount of source and the elastic properties of the geophysical medium [18].
with M0, the source radius r0, speed S—wave vS and static stress drop Δσ [15,16], as well as the similarity of the angular frequency f0 with a fundamental frequency of the acoustic Debye [17] fD, depending on the amount of source and the elastic properties of the geophysical medium [18].
Our further quantitative construction is based on the following empirical relationship Gutenberg and Richter [3,12]:
 (1)
(1)
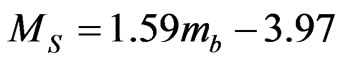 (2)
(2)
 (3)
(3)
where EGR—seismic energy according to Getenberg and Richter, J; t0—fluctuations with a maximum duration of vibration speed А/Т in the near field (А—amplitude, Т— period), s.
Use the following generalization of Soviet seismologists, which were introduced scale energy class KR [5], the magnitude of surface waves MLH (IC device) and body waves mPV on device SCM [4,9]:
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
where ER—seismic energy according to [5], in J; KR = log10ER; tm—increase the maximum duration of the seismic intensity in the near field, in sec.
The basis of the theoretical constructs are the following functional relations [10,13,15,16,19]:
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
where r0—radius of the source, in м; ∆σ—static seismic stress drop, in Pа; tb—corner period, s; MW—moment magnitude; (ESK, in J; M0, in N∙m; u in m; vS in m/s); for the constructions made t0 = tb = tm.
Many generalizations proved that for a wide range of changes log10M0 or MW empirical correlations magnitude mb, ML and MS from M0 are non-linear, as in Equation (8), as a function of  value of n varies from 3 to 6, and is increase Δσ [7,12,20-24].
value of n varies from 3 to 6, and is increase Δσ [7,12,20-24].
However, for individual intervals M0 or MW communication between magnitudes relationships and dependencies of the magnitude log10M0 can be represented as linear relationships.
2. Justification Relations Magnitude—Seismic Moment
Based on the original definition of magnitude on Richter [25], under which the numerical value of the earthquake magnitude is proportional to the logarithm of the maximum oscillation decimal вm, expressed in microns (10−6м), it is assumed that an upgraded body-wave magnitude mbm (equivalent mb, mPV ) is (considering doubling вm on the ground at the focus):
 (12)
(12)
If  in (8) on the basis Equations (9) and (10) and Equation (12) value mbm equal (M0, N∙m; tв, s; µ, Pa; vs, m/s):
in (8) on the basis Equations (9) and (10) and Equation (12) value mbm equal (M0, N∙m; tв, s; µ, Pa; vs, m/s):
 (13)
(13)
where , value С1 determines the springiness of the geophysical environment at mbm.
, value С1 determines the springiness of the geophysical environment at mbm.
Based on generalizations Christensen [26,27] for the crust taken: average density
ρ = 2830 kg/m3, vS = 3600 m/s and  in what follows, these quantities ρ, vs and μ taken as the standard.
in what follows, these quantities ρ, vs and μ taken as the standard.
When these elastic parameters of the geophysical medium expression Equation (13) is transformed to the following form:
 (14)
(14)
Seismic energy radiation ESK by Kanamori [19], based on Equations (8) and (9) and Equation (13) is:
 (15)
(15)
where .
.
Taken for the elastic parameters and subject [19].  obtain: Δσ = 3.67 MPa and 36.7 bar and the expression Equation (8) can be rewritten in a simple form log10t0 = 1/3log10M0 – 5.43, then Equation (15) simplifies to:
obtain: Δσ = 3.67 MPa and 36.7 bar and the expression Equation (8) can be rewritten in a simple form log10t0 = 1/3log10M0 – 5.43, then Equation (15) simplifies to:
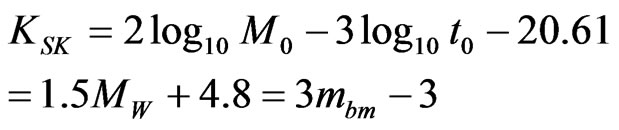 (16)
(16)
On the basis of Equations (13)-(16), reflecting the functional relationship of ESK from M0, t0, mbm and μ at EGR = ESK introduced upgraded the magnitude of surface waves MSm (equivalent of MS, MW), while maintaining that the formula Equation (1) Gutenberg and Richter [2,3], with Equation (9), Equations (15) and (16) will be:
 (17)
(17)
where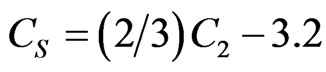 .
.
Taken for ρ and vS CS value in Equation (17) is equal to CS = –16.95, and for the special case of Δσ = 3.67 MPa = const and ESK/M0 = 5 × 10–5 equality: MSm = MW.
We also introduce a modernized local magnitude on surface waves MLm—equivalent ML [18,28], functionally interconnected with log10M0, logt0, KSK, mbm and MSm:
 (18)
(18)
where CL = 0.5 (C1 + CS): for standard values ρ and vS value CL is equal: CL = –14.12.
Accepted values for ρ and vS by Equation (8) and Equation (9) the following relationship:
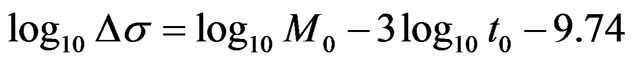 (19)
(19)
With the standard values ρ, vS and Δσ = 3.67 MPa, based on Equation (14) and Equation (17) we obtain the following theoretical relation:
 (20)
(20)
which is within the accuracy of the definitions of the same magnitude satisfactory empirical relation refined body wave magnitude  of MW for large earthquakes [19,29] (mb ≥ 6):
of MW for large earthquakes [19,29] (mb ≥ 6):
 (21)
(21)
which were used  to calculate the true maximum oscillation amplitude Ag, taken from seismograms;
to calculate the true maximum oscillation amplitude Ag, taken from seismograms; .
.
Here it should be emphasized that at a constant value of Δσ Equation (12) and Equation (14) the value of the maximum amplitude вm is proportional to  or
or  , that closely coincides with
, that closely coincides with  on [19,29].
on [19,29].
In the sequel will be shown .
.
Equation (20) agrees satisfactorily with other empirical relationship [9]
(mPV = mb + 0.18):
 (22)
(22)
The above quantitative ratios indicate that between modernized magnitudes Mm (mbm, MLm, MSm) and log10M0 may exist linear functional relationship of the form:
 (23)
(23)
in which the coefficients ki and zi at the control parameter at and вt in the ratio:
 (24)
(24)
where ∆σ = const = 3.67 МPa вt = 1/3 = const and at = –5.43, but for other cases вt is not a constant.
In view of Equations (23) and (24) correlations Equations (14), (17) and Equation (18) for mbm, MSm and MLm (standard values ρ and vS) can be written as follows:
 (25)
(25)
 (26)
(26)
 (27)
(27)
which provide a self-consistent system of semi empirical inter magnitude dependencies. For example, the dependence of mвm from MSm based on Equations (25) and (26) can be expressed as:
 (28)
(28)
which is вt = 0.33 and at = −5.43 ransformed into simple formula Equation (20).
3. Discussion of Empirical and Theoretical Relations Magnitude—Seismic Moment
Local magnitude—seismic moment. Since the value of the local magnitude is directly related to the maximum oscillation amplitude of the surface waves and the first inter magnitude connections [2,3] have been developed for California earthquakes, relations ML – consider according to Thatcher and Hanks [30] in this region (2 ≤ ML ≤ 6.8).
consider according to Thatcher and Hanks [30] in this region (2 ≤ ML ≤ 6.8).
For this region, the authors have taken ρ = 2700 kg/m3 and vS = 3200 m/s, and by (13) and (17) a constant values will be: С1= −11.09, СS = −16.5, СL = −13.72. With known ρ, vs, Δσ/2μ = 5 × 10−5 between log10t0 and log10M0 would expect the following relationship: , but the instrumental data obtained (Figure 1, N—the number of data, r—correlation coefficient):
, but the instrumental data obtained (Figure 1, N—the number of data, r—correlation coefficient):
 (29)
(29)
i.e. in accordance with (19) with increasing values of M0log10Δσ increases:
 . Therefore, for the considered data characteristic dependence
. Therefore, for the considered data characteristic dependence , said Nuttli [12] for mid-plate earthquakes.
, said Nuttli [12] for mid-plate earthquakes.
If true theoretical Equations (13), (17) and (18), then

Figure 1. Correlation of log10t0 from log10M0 for Southern California earthquakes according to Thatcher and Hanks [30] ( , N = 138, r = 0.84).
, N = 138, r = 0.84).
Equation (29) and the relationship between MLm and log10t0 is given by:
 (30)
(30)
which is in good agreement with the expression (3) Gutenberg and Richter [2] and Equation (5) Soviet seismologists [31] which allows to consider t0 = tв = tm.
In Figure 2 shows the correlation log10t0 and ML according to Thatcher [30], which also shows the relationship Equation (3) and Equation (30). The presented data show that the semi-empirical formula Equation (30) is in good agreement with generalizations instrumental data (Figure 2). It should also be noted that the ML = MLm based on Equation (3) Gutenberg and Richter [2], and Equation (18) can be obtained
 (31)
(31)
which is in satisfactory agreement with the expression (29).
In Figure 3 in the range of 0.5 ≤ ML ≤ 6.8 shows the correlation ratio MLm of ML for Southern California earthquakes [30], South-West Germany [32] and Central Japan [33]. In calculations MLm by Equation (18) for the earthquakes in these regions were considered elastic parameters of the geophysical medium according to these authors. The statistical data confirm the validity of our assumptions on the possible equality ML and MLm (Figure 3).

Figure 2. Correlation of log10t0 from ML for Southern California earthquakes according to Thatcher and Hanks [30], full line: , N = 138, r = 0.84. Dashed line—
, N = 138, r = 0.84. Dashed line— by Gutenberg and Richter (1956а); dot-dash line—dependence log10t0 from MLm, obtained from correlation log10t0 from log10M0 (Figure 1).
by Gutenberg and Richter (1956а); dot-dash line—dependence log10t0 from MLm, obtained from correlation log10t0 from log10M0 (Figure 1).

Figure 3. The ratio of calculated MLm and instrumental ML for Southern California earthquakes by Thatcher and Hanks [30], South-West Germany (Scherbaum et al. 1983) and Cental Japan (Jin et al., 2000). , N = 384, r = 0.94; dashed line MLm = ML.
, N = 384, r = 0.94; dashed line MLm = ML.
From numerous publications on nonlinear relations log10M0 – ML acceptability of new assumptions considered on the basis of Hasegawa [34] for earthquakes in Eastern Canada. In the range 0 < ML ≤ 6.3 are two of the interval 0 < ML ≤ 3.9 and 3.9 ≤ ML ≤ 6.3, which have different dependencies on log10t0 of ML and log10M0 from ML [34].
For the first group of small earthquakes characterized by the following relationship (105 < ∆σ < 106 Pа): , but for another group (106 ≤ ∆σ < 5 × 106 Pа):
, but for another group (106 ≤ ∆σ < 5 × 106 Pа): .
.
On the basis of these empirical formulas for Equation (18) and Equation (24) with CL = −14.21 (ρ = 2800 kg/m3 and vs = 3800 m/s) Figures 4 and 5 shows the calculated dependences of log10t0 from MLm and log10M0 from MLm, which in satisfactory agreement with the relations log10t0 − ML and log10M0 − ML (Figures 4 and 5) by Hasegawa [34].
Finally, for the Southern California Earthquake Equation (18) and Equation (29) we can obtain the following relationship: , which coincides with the ratio of [30]:
, which coincides with the ratio of [30]:
 (32)
(32)
According to Equations (23) and (24) and Equation (27) if вt = 0.25 we get , which indicates the acceptability of the proposed relations.
, which indicates the acceptability of the proposed relations.
From Equation (32) it follows that bt = 0.25 in Equation (24) the values of ML and MLm magnitude MW corresponds to Equation (11). Probably, the presence of the form Equation (29) between log10t0 and log10M0 explains equality ML = MW for earthquakes with MW ≤ 7.0 NorthWest Europe [35], New Zealand [36], western Canada [37] and about Taiwan [38].
3.1. Ratio mb − log10M0: Design and Data Tools
As in the case of search based ML − log10M0, for bodywave magnitude mb consider empirical relationships According to Zapolsky [31], Gutenberg [1], specifically examining the relationship between the energy of focal radiation and earthquake magnitude according to

Figure 4. Correlation log10t0 from ML (full line—Hasegawa [34] and from calculated MLm (dashed line, see the text) for East Canada earthquakes.

Figure 5. Correlation log10M0 from ML (full line—Hasegawa [34] and from calculated MLm (dashed line, see the text) for East Canada earthquakes.
the observations in the epicentral area, showed that the duration t0, determine the energy of the oscillations with the maximum intensity depends strongly on the magnitude and 2.5-fold increases with increasing magnitude of mb on unit [31].
 (33)
(33)
A little-known empirical formula Equation (32) Gutenberg [1] is a key for further generalizations of our constructions on relations mb − log10M0, and mb − MS.
On the basis of (13) and (29) with С1 = −11.09, we can get:
 (34)
(34)
Substitution  in Equation (31) into (13) leads to the following formula:
in Equation (31) into (13) leads to the following formula:
 (35)
(35)
which is in good agreement with (33) provided mb = mbm.
Graphic expressions Equations (33)-(35) are shown in Figure 6, from which it can be assumed about the close convergence of these relations and the possible equality mb = mbm (Figure 6). At equality mb = mbm—based Equations (13) and (33) for the standard ρ and vS can obtain the expression:
 (36)
(36)
which is in good agreement with Equations (29) and (31), which may indicate the consistency of our constructions relating mb, mbm, ML, MLm and log10t0 with log10M0 for earthquakes in California, despite the fact that the conclusions are based on statistical formulas in which the correlation coefficients are not equal to unity (r = 0.75 - 0.90)
If we use the Equation (36), on the basis of Equation (24) with вt = 0.22 and Equations (25) and (26) for the

Figure 6. Correlation log10t0 and mb (full line), log10t0 and mbm (dashed line, see the text).
standard values ρ and vS, MSm dependence on mbm can be expressed as:
 (37)
(37)
which almost corresponds to the classical formula Equation (2) Gutenberg and Richter (1956в) and for which the equality MSm = mbm complied with Msm = 5.40, which coincides closely with generalizations Chen [7], Gusev [9], Nuttli [12] and Utsu [24].
In Figure 7 shows the correlation of log10t0 from log10M0 for earthquakes in the world (1981-1991) by the Catalogue Choy [39], for which the value of t0 was taken from the Global CMT Catalogue. The ratio of log10t0 from log10M0 for these data is given by (Figure 7):
 (38)
(38)
for which the range 17 ≤ log10M0 ≤ 21 value of log10Δσ by Equation (19) increases from 6.60 to 7.10.
Substituting (38) in (13) leads to (С1 = –11.30):
 (39)
(39)
which agrees closely with the empirical formula:
 (40)
(40)
shown on Figure 8.

Figure 7. Correlation dependence log10t0 from log10M0 for major earthquakes of the world (1981-1991) by Choy’s Catalogue [39]. , N = 379, r = 0.96.
, N = 379, r = 0.96.

Figure 8. Correlation dependence mb from log10M0 (full line) for major earthquakes of the world (1981-1991) by Choy’s Catalogue et al. (1995) for 1981-1991.  , N = 362, r = 0.67, dashed line—calculated dependence:
, N = 362, r = 0.67, dashed line—calculated dependence:  .
.
Equation (39) is in good agreement with the dependence on mb from log10M0 for Sumatra island earthquake (φ = –10˚ + 10˚, λ = +90˚ + 100˚) for 1993-2012 (Figure 9).
Table 1 shows a comparison of the magnitude  obtained by the true maximum amplitude [19,29,40] and the calculated value mbm (Table 1) for a number of large earthquakes in 1960-1984. The presented data suggest that for most of the earthquakes characterized by the following inequality:
obtained by the true maximum amplitude [19,29,40] and the calculated value mbm (Table 1) for a number of large earthquakes in 1960-1984. The presented data suggest that for most of the earthquakes characterized by the following inequality: .
.
When log10Δσ ≥ 7.1 value of  is close to the mbm same as for Great Chilean earthquake
is close to the mbm same as for Great Chilean earthquake  and mbm = 7.71, for Tangshan (1976)
and mbm = 7.71, for Tangshan (1976)  and mbm = 6.92, Yanyuan (1976).
and mbm = 6.92, Yanyuan (1976). , mbm = 6.18, and if 6.36 ≤ log10∆σ < 7.0 value of
, mbm = 6.18, and if 6.36 ≤ log10∆σ < 7.0 value of 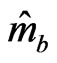 more then mbm (Table 1).
more then mbm (Table 1).
Table 2 presents a comparison of calculated mbm and  (21) for 80 major earthquakes of the world for 2000- 2012 for calculations mbm,
(21) for 80 major earthquakes of the world for 2000- 2012 for calculations mbm,  and MSm used data from Global CMT Catalogue (Table 2). When comparing log10Δσ from Table 1 to Table 2 shows that with increasing log10M0 from 19.15 to 22.72 for the 2000-2012 earthquakes log10Δσ value ranges from 6.75 - 7.58 with an average of 7.16, that is, much higher than for earthquakes 1960-1984 (Tables 1 and 2) and higher than the standard logΔσ = 6.56.
and MSm used data from Global CMT Catalogue (Table 2). When comparing log10Δσ from Table 1 to Table 2 shows that with increasing log10M0 from 19.15 to 22.72 for the 2000-2012 earthquakes log10Δσ value ranges from 6.75 - 7.58 with an average of 7.16, that is, much higher than for earthquakes 1960-1984 (Tables 1 and 2) and higher than the standard logΔσ = 6.56.
For such high values Δσ values mbm closely coincide with the design , and for values MSm characterized by inequality: MSm > MW (Table 2) confirmed that conclusion is the relation mbm −
, and for values MSm characterized by inequality: MSm > MW (Table 2) confirmed that conclusion is the relation mbm − —for earthquakes in Japan and the Kuril Islands (φ = 30˚ + 40˚, λ = 140˚ + 150˚) for the 1993-2012 shown in Figure 10.
—for earthquakes in Japan and the Kuril Islands (φ = 30˚ + 40˚, λ = 140˚ + 150˚) for the 1993-2012 shown in Figure 10.
Thus for large earthquakes 1960-1984 and 1993-2012 at logΔσ > 7.1 mbm values coincide closely with the magnitude  calculated from the true maximum amplitude (Ag) of seismic vibrations, the magnitude of which is proportional to the seismic moment:
calculated from the true maximum amplitude (Ag) of seismic vibrations, the magnitude of which is proportional to the seismic moment:  to Houston [29] and Kanamori [19]. Consequently, the mbm
to Houston [29] and Kanamori [19]. Consequently, the mbm
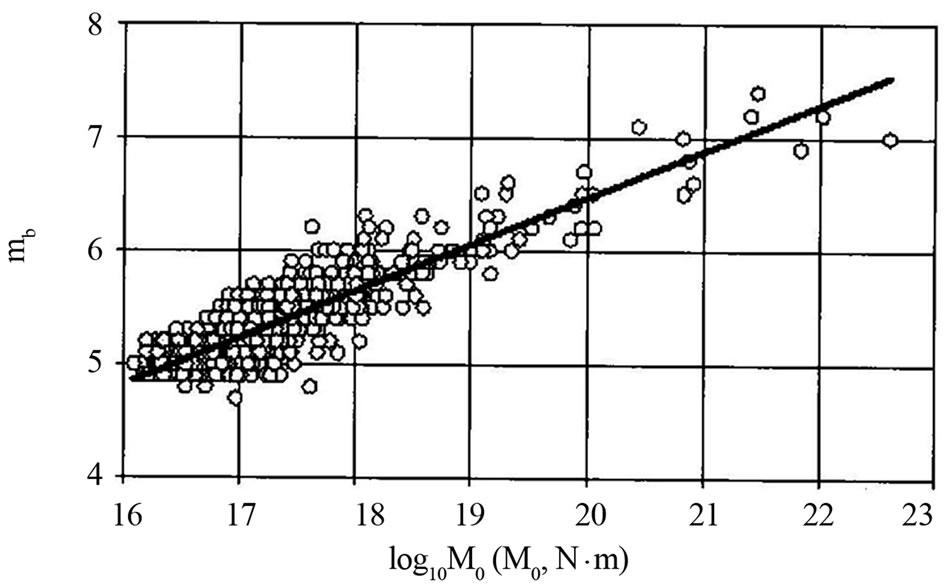
Figure 9. Correlation dependence mb from log10M0 for the earthquakes Sumatra region (1993-2012 years).  , N = 631, r = 0.88.
, N = 631, r = 0.88.

Figure 10. Correlation calculated magnitudes mbm and  for the earthquakes in Japan and Kuril Islands for 1992- 2012 years.
for the earthquakes in Japan and Kuril Islands for 1992- 2012 years. , N = 521, r = 0.97. Values of
, N = 521, r = 0.97. Values of  were calculated according to the formula (21).
were calculated according to the formula (21).
value is proportional to the log10Аg.
The ratio of MS – log10M0. In Mamyrov’s papers [18], [28] have shown that in the range of 16 ≤ log10M0 < 21.0 if log10Δσ ≤ 7.0 at the rated MSm closely coincides with MS and MW, and for high Δσ ≥ 107 Pa following inequality MSm > MS, as shown in Table 2.
In Figure 11 shows the correlation of MS from log10M0 for earthquakes of the world for 1981-1991 according to the Catalog Chou et al. [39]:
 (41)
(41)
which is in satisfactory agreement with the dependence  (Figure 11, dashed line), derived from Equations (38) and (26). These relations with MS = MSm with log10M0 are in good agreement with the generalization of Perez [41] for crustal earthquakes of the world for the years 1950-1997:
(Figure 11, dashed line), derived from Equations (38) and (26). These relations with MS = MSm with log10M0 are in good agreement with the generalization of Perez [41] for crustal earthquakes of the world for the years 1950-1997:  .
.
In Figure 12 shows the correlation MS with log10M0 (solid line) for the earthquakes in Japan and the Kuril Islands in 1993-2012:
 , here, we show the same relationship MSm from log10M0 (Figure 12, dashed line):
, here, we show the same relationship MSm from log10M0 (Figure 12, dashed line):
 , obtained with (N = 521, r = 0.99):
, obtained with (N = 521, r = 0.99):


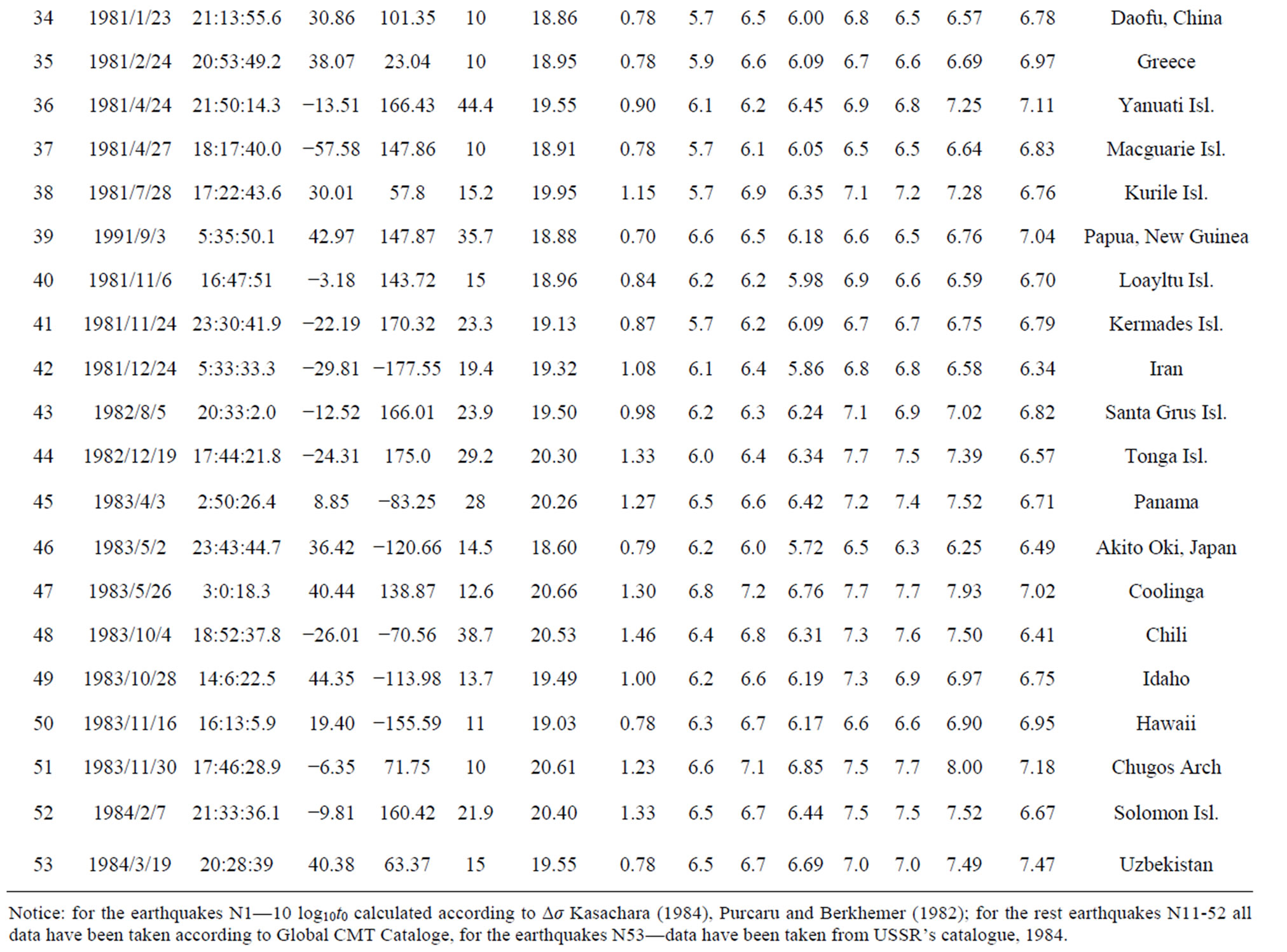
Table 1. A comparison of the magnitude  (Houston, Kanamori, 1986; Zhuo, Kanamori, 1987) and settlement mbm for several major earthquakes of the world.
(Houston, Kanamori, 1986; Zhuo, Kanamori, 1987) and settlement mbm for several major earthquakes of the world.

Figure 11. Correlation of magnitudes MS and log10M0 (full line) by Catalogue of major earthquakes of the world Choy [39]: , N = 372, r =0.93. Dashed line—calculated dependence.
, N = 372, r =0.93. Dashed line—calculated dependence.  .
.

Figure 12. Correlation dependence of magnitude MS from log10M0 for the earthquakes in Japan and Kuril Islands for 1993-2012 years. , N = 514, r = 0.95. Dashed line—calculated dependence.
, N = 514, r = 0.95. Dashed line—calculated dependence. .
.




Table 2. Comparison of calculated (mbm, MSm) and instrumental (mb, MS, MW) for a number of magnitude large earthquakes of the world 2000-2012 years.
 (42)
(42)
From the data that the value MSm an average of 0.5 more than the MS, because according to the relation log10t0 with log10M0 (from 42) with growth log10M0 from 16 to 22 on the basis of (19), the value increases from 7.19 logΔσ to 7.43 (Figure 12), and using equation (38) in the same size ranges of log10M0 the value of log10∆σ increases from 6.5 to 7.10. It is likely that for most crustal earthquakes before 1993 was characterized by the above limits to growth log10∆σ < 7.10.
Ratio mb – MS и mbm – MSm. In Figure 13 shows the correlation ratio mb – MS for crustal earthquakes of the Kuril Islands and Japan for 1993-2011:
 (43)
(43)
which is in good agreement with the expression:
 (44)
(44)
derived from (42) and (28) for вt = 0.32 и at = −5,43 (Figure 13).
Figure 14 shows the correlation ratio mb – MS for crustal earthquakes in South America for the years 1993- 2012, (φ = −40˚ − 0˚, λ = −85˚ − 65˚) by Global CMT Catalogue:
 (45)
(45)
for this region was obtained (N = 576, r = 0.99):
 (46)
(46)
the substitution of which in (26), вt = 0.32 and at = −5.48 leads to the formula
 (47)
(47)
Equations (43)-(46) are in good agreement with Equations (21) and (22).
Figure 15 shows the correlation log10t0 of log10M0 for earthquakes of the Tien Shan (φ = 38.5˚ − 45˚, λ = 63˚ − 96˚) for 1960-2012 in interval 13.0 ≤ log10M0 ≤ 21.5 (N = 684, r = 0.85):
 (48)
(48)
which closely coincides with Equations (29), (31) and (36) typical for earthquakes in California (Figures 1 and 15).
Therefore, we can expect that the relationship between magnitudes mb – MS for earthquakes of the two regions may be similar in this range of seismic moment. Indeed, the data in Figure 16 confirmed these assumptions and empirical relationship of MS from mb for Tien Shan’s earthquakes is expressed by the following relation (N = 1183, r = 0.95, Figure 16):
 (49)
(49)

Figure 13. Correlation of magnitudes mb and MS for the earthquakes in Japan and Kuril Islands for 1993-2012 years. , N = 514, r = 0.84. Calculated dependence
, N = 514, r = 0.84. Calculated dependence  if
if  (see text).
(see text).

Figure 14. Correlation of magnitudes mb and MS for the earthquakes in South America 1993-2012 years.  , N = 547, r = 0.82. Calculated dependence
, N = 547, r = 0.82. Calculated dependence  if
if  (see text).
(see text).
Calculated dependence of MSm from mbm based on Equations (25), (26) and (47) for the elastic parameters of the standard as follows:
 (50)
(50)
which is in good agreement with Equations (2), (37) and (49).
Therefore, we have adopted model of the relationship of linear relations between M (mb, ML, MS) and log10t0 with log10M0 explains many existing empirical formulas. For a wide range 6 ≤ log10M0 ≤ 23 changing log10t0, to a first approximation, can be described by a nonlinear dependence of (A0 = log10M0):
 (51)
(51)
in which the first two terms describes the linear growth log10t0 in the range 6 ≤ A0 ≤ 15. On the basis of Equations (25)-(27) and (51) in Figure 17 shows estimates nonlinear dependence mbm, MLm and MSm from MW to (11) for crustal earthquakes. From Figure 17 shows that in the

Figure 15. Correlation dependence log10t0 from log10M0 for Tien Shan earthquakes (1960-2012 years).  , N = 684, r = 0.85.
, N = 684, r = 0.85.

Figure 16. Correlation of magnitudes MS and mb for Tien Shan earthquakes (1902-2012 years).  , N = 1183, r = 0.95. Calculated dependence
, N = 1183, r = 0.95. Calculated dependence  if
if  (see the text).
(see the text).

Figure 17. Averaged according MSm MLm and mbm from MW for crustal earthquakes (see text), the dashed line represents the intersection of the curves MSm » MLm » mbm » MW » 5.26 − 5.50.
interval 4 ≤ MW ≤ 6,5 numerical values of magnitudes mbm » mb, MLm » ML, MSm » MS and MW within the accuracy of these parameters are close. In accordance with Equations (19) and (51) in the interval 6.0 < A ≤ 23.0 log10∆σ value increases from 1.75 to 7.53, and the most intense increase in this parameter is in the range 6.0 ≤ A0 ≤ 15.0.
4. Conclusions
1) A broad range of local Richter magnitude ML, mb, and MS crustal earthquakes in different regions shows a possible functional relationship with the seismic moment magnitude, corner frequency, voltage and depressurized seismic elastic parameters of the geophysical environment. These links justify numerous empirical relationships with magnitudes of seismic moment.
2) It is assumed that an upgraded body-wave magnitude mbm for large earthquakes is proportional to the logarithm of the average displacement along the fault log10u,  , the true magnitude and the maximum amplitude of seismic vibrations Ag; magnitude MSm is proportional to the logarithm of the square average displacement along the fault (2log10u) and local magnitude proportional 1.5log10u.
, the true magnitude and the maximum amplitude of seismic vibrations Ag; magnitude MSm is proportional to the logarithm of the square average displacement along the fault (2log10u) and local magnitude proportional 1.5log10u.
3) Control parameters of the quantitative relations with seismic moment magnitudes are coefficients depending on the change in corner period of seismic stress drop or discharged from the seismic moment, which provide a self-consistent system of equations between the main source parameters of crustal earthquakes.
REFERENCES
- B. Gutenberg, “Amplitudes of P, PP, an S waves and Magnitude of Shallow Earthquakes,” Bulletin of the Seismological Society of America, Vol. 35, No. 2, 1945, pp. 57-69.
- B. Gutenberg and C. F. Richter, “Earthquake Magnitude, Intensity, Energy and Acceleration,” Bulletin of the Seismological Society of America, Vol. 46, No. 2, 1956, pp. 105-145.
- В. Gutenberg and C. F. Richter, “Magnitude and Energy of Earthquakes,” Annali di Geofisica, Vol. 9, No. 1, 1956, pp. 1-15.
- N. V. Kondorskaya, A. I. Zakharova and L. S. Chepkunas, “The Quantitative Characteristics of Earthquake Sources as Determined in the Seismological Practice of the U.S.S. R.,” Tectonophysics, Vol. 166, No. 1-3, 1989, pp. 45-52. doi:10.1016/0040-1951(89)90204-7
- T. G. Rautian, “Energy of Earthquakes,” In: Y. V. Riznichenko, Ed., Methods for the Detailed Study of Seismicity, Akademii Nauk SSSR, Moscow, 1960, pp. 75-114.
- T. G. Rautian, V. J. Khalturin, K. Fujita, K. G. Mackey, et al., “Origins and Methodology of the Russian Energy K-Class System and Its Relationship to Magnitude Scales,” Seismological Research Letters, Vol. 78, No. 6, 2007, pp. 579-590. doi:10.1785/gssrl.78.6.579
- P. Chen and H. Chen, “Scaling Law and Its Applications to Earthquake Statistical Relations,” Tectonophysics, Vol. 166, No. 1-3, 1989, pp. 53-72. doi:10.1016/0040-1951(89)90205-9
- L. B. Grant, “Paleoseismology, International Handbook of Earthquake and Engineering Seismology, Part A,” Academic Press, Waltham, 2002.
- A. A. Gusev and V. N. Melnikova, “Relations between Magnitudes: Global and Kamchatka Data,” Volkanology and Seismology, Vol. 6, 1990, pp. 55-63.
- K. Kasahara, “Earthquake Mechanics,” 1985.
- P. Mai and G. C. Beroza, “Source Scaling Potpies from Finite-Fault-Rupture Models,” Bulletin of the Seismological Society of America, Vol. 90, No. 3, 2000, pp. 604- 615. doi:10.1785/0119990126
- O. W. Nuttli, “Average Seismic Source-Parameters Relation for Mid-Plate Earthquakes,” Bulletin of the Seismological Society of America, Vol. 73, No. 2, 1983, pp. 519- 535.
- K. Аki, “Generation and Propagation of G-Waves from the Niigata Earthquake of June 16, 1964. Part 2. Estimation of Earthquake Moment, Released Energy, and StressStrain Drop from the G-Wave Spectrum,” Bulletin of the Earthquake Research Institute, Tokyo, 1966.
- K. Aki and P. A. Richards, “Quantitative Seismology. Theory and Methods, v. t., Moskau: Mir,” 1983.
- J. N. Brune, “Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes,” Journal of Geophysical Research, Vol. 75, No. 26, 1970, pp. 4997-5009. doi:10.1029/JB075i026p04997
- V. Keilis-Borok, “On Estimation of the Displacement in an Earthquake Source and Dimension,” Annales Geophysicae, Vol. 12, No. 1-4, 1959, pp. 205-214.
- P. Debye, “Zur Theorie der Spezifischen Wärmen,” Annalen der Physik, Vol. 344, No. 14, 1912, pp. 789-839. doi:10.1002/andp.19123441404
- E. Mamyrov, “Relations among Earthquake Source Parameters Derived from Debye Solid-Body Model,” Journal of Geodynamics, Vol. 22, No. 1, 1996, pp. 137-143. doi:10.1016/0264-3707(96)00005-1
- H. Kanamori, “The Energy Released in Great Earthquakes,” Journal of Geophysical Research, Vol. 82, No. 20, 1977, pp. 2981-2987. doi:10.1029/JB082i020p02981
- G. A. Bollinger, M. C. Chapman and M. S. Sibol, “A Compassion of Earthquake Damage Areas a Function of Magnitude across the United States,” Bulletin of the Seismological Society of America, Vol. 83, 1993, pp. 1064- 1080.
- D. M. Boore, “The Richter Scale: Its Development and Use for Determining Earthquake Source Parameters,” Tectonophysics, Vol. 166, 1989, pp. 1-14. doi:10.1016/0040-1951(89)90200-X
- T. S. Hanks and D. M. Boore, “Moment-Magnitude Relations in Theory and Practice,” Journal of Geophysical Research, Vol. 89, No. B7, 1984, pp. 6229-6235. doi:10.1029/JB089iB07p06229
- E. M. Scordilis, “Empirical Global Relations Converting MS and mв to Moment Magnitude,” Journal of Seismology, Vol. 10, 2006, pp. 225-236. doi:10.1007/s10950-006-9012-4
- T. Utsu, “Relationships between Magnitude Scales, International Handbook of Earthquake and Engineering Seismology, Part A,” Academic Press, Waltham, 2002.
- C. F. Richter, “An Instrumental Earthquake Magnitude Scale,” Bulletin of the Seismological Society of America, Vol. 25, No. 1, 1935, pp. 1-32.
- N. I. Christensen, “Poisson’s Ratio and Crustal Seismology,” Journal of Geophysical Research, Vol. 101, No. B2, 1996, pp. 3139-3156. doi:10.1029/95JB03446
- N. I. Christensen and W. D. Mooney, “Seismic Velocity Structure and Composition of the Continental Crust: A Global View,” Journal of Geophysical Research, Vol. 100, No. B6, 1995, pp. 9761-9788. doi:10.1029/95JB00259
- E. Mamyrov, “New System of Quantitative Correlations between Seismic Energy, Magnitude and Energy of Seismic Radiation of the Crust Earthquakes in Tien Shan,” The 33rd General Assembly of the European Seismological Commission, Moscow, 19-24 August 2012, pp. 29-30.
- H. Houston and H. Kanamori, “Source Spectra of Great Earthquakes: Teleseismic Constraints on Rupture Process and Strong Motion,” Bulletin of the Seismological Society of America, Vol. 76, No. 1, 1986, pp. 19-42.
- W. Thatcher and C. Hahks, “Source Parameters of Southern California Earthquakes,” Journal of Geophysical Research, Vol. 78, No. 35, 1973, pp. 8547-8575. doi:10.1029/JB078i035p08547
- K. K. Zapolskii, J. L. Nersesov, T. G. Rautian and V. I. Halturin, “Physical Basis of Magnitude Classification of Earthquakes,” 1974.
- F. Scherbaum and D. Stoll, “Source Parameters and Scaling Laws of the 1978 Schwabian Jura (Southwest Germany) Aftershocks,” Bulletin of the Seismological Society of America, Vol. 73, No. 5, 1983, pp. 1321-1343.
- A. Jin, C. A. Moya and M. Ando, “Simultaneous Determination of Site Responses and Source Parameters of Small Earthquakes along the Atotsugawa Fault Zone, Central Japan,” Bulletin of the Seismological Society of America, Vol. 90, No. 6, 2000, pp. 1430-1445. doi:10.1785/0119990140
- H. S. Hasegawa, “Lg-Spectra of Local Earthquake Recorder by the Eastern Canada Telemeters Network and Spectral Scaling,” Bulletin of the Seismological Society of America, Vol. 73, 1983, pp. 1041-1061.
- G. Grunthal and R. Wahlstrom, “An MW Based Earthquake Catalogue for Central, Northern and North-Western Europe Using a Hierarchy of Magnitude Conversions,” Journal of Seismology, Vol. 7, No. 4, 2003, pp. 507-531. doi:10.1023/B:JOSE.0000005715.87363.13
- J. G. Ristau, G. C. Rogers and F. Cassidy, “Moment Magnitude-Local Magnitude Calibration for Earthquake in Western Canada,” Bulletin of the Seismological Society of America, Vol. 95, No. 5, 2005, pp. 1994-2000. doi:10.1785/0120050028
- J. Ristau, “Comparison of Magnitude Estimates for New Zealand Earthquakes: Moment Magnitude, Local Magnitude, and Teleseismic Body-Wave Magnitude,” Bulletin of the Seismological Society of America, Vol. 99, No. 3, 2009, pp. 1841-1852. doi:10.1785/0120080237
- Y. M. Wu, R. M. Allen and C. W. Wu, “Revised ML Determination for Crustal Earthquake in Taiwan,” Bulletin of the Seismological Society of America, Vol. 95, No. 6, 2005, pp. 2517-2524. doi:10.1785/0120050043
- G. L. Choy and J. Boatwright, “Global Patterns of Radiated Seismic Energy and Apparent Stress,” Journal of Geophysical Research, Vol. 100, No. B9, 1995, 18205- 18228. doi:10.1029/95JB01969
- Y. Zhuo and H. Kanamori, “Regional Variation of the Short-Period (1 to 10 Second) Source Spectrum,” Bulletin of the Seismological Society of America, Vol. 77, No. 2, 1987, pp. 514-529.
- O. J. Perez, “Revised World Seismicity Catalog (1950- 1997) for Strong (MS≥6) Shallow (h£70 km) Earthquakes,” Bulletin of the Seismological Society of America, Vol. 89, No. 2, 1999, 335-341.

