Open Journal of Optimization
Vol.04 No.04(2015), Article ID:62250,12 pages
10.4236/ojop.2015.44015
Hybrid Genetic Algorithm and Variable Neighborhood Search for Dynamic Facility Layout Problem
Md Sanuwar Uddin
Department of Mechanical Engineering, Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 November 2015; accepted 22 December 2015; published 25 December 2015
ABSTRACT
This paper presents a novel hybrid metaheuristic GA-VNS matching genetic algorithm (GA) and variable neighborhood search (VNS) to the dynamic facility layout problem (DFLP). The DFLP is a well-known NP hard problem which aims at assigning a set of facilities to a set of locations over a time planning horizon so that the total cost including material handling cost and re-arrangement cost is minimized. The proposed hybrid approach in this paper elegantly integrates the exploitation ability of VNS and exploration ability of GA. To examine the performance of the proposed hybrid approach, a set of instance problems have been used from the literature. As demonstrated in the results, the GA-VNS is mighty of attaining high quality solution. Compared with some state-of- the-art algorithms, our proposed hybrid approach is competitive.
Keywords:
Dynamic Facility Layout, Genetic Algorithm, Material Handling

1. Introduction
The DFLP is the determination of the most efficient arrangement of a number of facilities on the plant floor over multiple periods so that the sum of material handling cost and re-arrangement cost is minimized. The DFLP is an extension of static facility layout problem (SFLP) by considering changes in material flow between facilities over time planning periods. The main issue with DFLP is the existence of time period that makes it more complex than SFLP. Historically, most of the research conducted on facility layout problem has been focused on SFLP type; however nowadays there is a necessity of considering dynamic condition due to demand of flexibility and rapid changes on manufacturing systems. For instance, high tech industries such as electronics and software developments need to be designed under a dynamic environment rather than static due to changes on their product design and functionalities. Therefore the static layout is unreliable and economically inefficient for such industries.
In the DFLP, time period can be expressed in terms of week, month or even year. Solution of SFLP consists of a single layout while it is a series of layout (layout map) with each layout is associated with a particular period for the DFLP [1] . It is important to notice that the DFLP can be converted to SFLP if and only if one of circumstances given below occurs:
・ If material handling costs are extremely larger than re-arrangement costs, then DFLP can be solved as a series of SFLP. In fact, the optimum layout associated with first period can be attained by solving the SFLP using data for the first period and the optimum solution for the second period can be similarly attained by solving the SFLP using data for the second time period and so on.
・ If re-arrangement cost is extremely larger than handling costs, so the handling cost can be simply ignored and the problem can be solved as a series of SFLP.
So the DFLP deals with selecting a set of layout for each period and then deciding whether a facility needs to be re-arranged in the next period or remains fixed. It is clear that the layout configuration tends to be fixed if the re-arrangement cost is high while there are more tendencies toward changing layout plan over the time horizon if the re-arrangement cost is low. The assumptions of DFLP are defined as follows: the flow between facilities is dynamic and deterministic; facilities and locations are all equal size; the distances between facilities are predetermined [1] .
2. Literature Review
The DFLP was initially addressed by Rosenblatt [2] in 1986. He applied dynamic programing (DP) as an exact approach to solve the DFLP. As pointed out previously, DFLP is an extension of SFLP. SFLP with n facilities has (n!) possible layouts (solutions) while the DFLP with n facilities and T time period has (n!)T possible layout maps. It is easy to see that the complexity of DFLP is much larger than SFLP and hence, is computationally intractable. Therefore the results achieved by decent exact methods such as branch and bound are modest. This is the reason there is intense motivation to implement heuristics to solve DFLP. Thereby the major portion of the literature is dedicated to review heuristics approaches.
Lacksonen and Enscore [3] developed a heuristic based on a dynamic programming (DP) approach presented by Rosenblatt [2] . Baykasoglu and Gindy [4] proposed a simulated annealing (SA) for solving the DFLP. Balakrishnan et al. [5] applied a hybrid genetic algorithm. The role of crossover operator is taken by DP and CRAFT is used for the mutation purpose. Dunker et al. [6] extended the GA proposed by Dunker et al. [7] for solving the DFLP with unequal area facilities. The approach is based on integrating dynamic programming and genetic algorithm. Dynamic programming is used for the purpose of evaluating the fitness of layouts. McKendall et al. [1] proposed two simulated annealing SAI, and SAII. SA I is an adaption of SA to the DFLP while the SA II is the same as SAI with extra feature of look-ahead/look-back strategy. McKendall and Shang [8] presented hybrid ant systems (HAS) for the DFLP. Their hybrid consists of two heuristics HAS I and HAS II. HAS I is a simple ant colony algorithm with random decent exchange heuristic while the concept of local search using SA is incorporated with HAS II. McKendall and Hakobyan [9] developed a boundary search technique to place unequal size facilities. The Tabu search (TS) is used to improve the solution. Chen [10] proposed a new data structure to code solution representation. The new data structure improves the solution swapping and sorting activities and also remarkably reduces the computational cost. Guan and Lin. [11] presented a hybrid variable neighborhood search with ant colony optimization for solving the single row facility layout problem. Baykasoglu et al. [12] applied ant colony optimization (ACO) to solve DFLP with budget constraints consideration. Their work considers budget constraint limitation for re-arrangements over planning horizon. Sahin et al. [13] implemented SA for solving the DFLP with budget constraint. Ulutas and Kulturel-Konak [14] presented an artificial immune system (AIS) to solve unequal area facility layout with flexible bay structure. In order to fill the empty space between facilities, the used a new encoding scheme. Komarudin and Wong [15] applied ACO to tackle with DFLP with unequal area facility. The authors used slicing tree representation which prevents restricting too much solution space. Ripon et al. [16] applied an adaptive variable neighborhood search for solving multi-ob- jective facility layout problems with unequal area facilities. Their proposed approach is based on extending conventional local search which determines whether the VNS is used in a GA loop or not. Kulturel-Konak [17] presented a probabilistic TS approach for solving facility layout problem with unequal departments with flexible bay structures. A brief review of developed approach in the related literature is presented in Table 1. Hosseini et al. [18] developed a hybrid imperialist competitive algorithm (ICA), variable neighborhood search (VNS), and simulated annealing (SA) to deal with complexity of DFLP. More applications of meta-heuristic algorithm for facility layout design can be found in [19] -[29] .
The mathematical model of DFLP presented by McKendall et al. [1] is given below:
 (1)
(1)
s.t.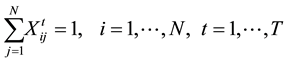 (2)
(2)
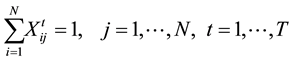 (3)
(3)
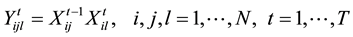 (4)
(4)
 (5)
(5)
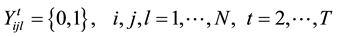 (6)
(6)
Notations which are used to describe the DFLP model are defined below:
Table 1. A brief review of the research papers in the related literature.
2.1. Indexes
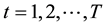 where T is the number of periods
where T is the number of periods
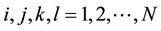 where N is the number of facilities
where N is the number of facilities
2.2. Parameters
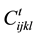 cost of material flow between facility i from location j to l in period t
cost of material flow between facility i from location j to l in period t
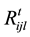 cost of re-arranging facility i from location j to location l at time period t
cost of re-arranging facility i from location j to location l at time period t
2.3. Decision Variables
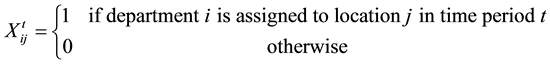
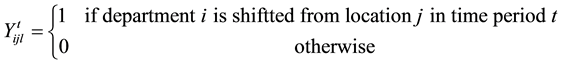
The first term in objective function (1) represents the material handling costs, and the second term is used to obtain the re-arrangement costs. Constraint set (2) guarantees that each location is assigned to only one facility at each time period. Constraint set (3) guarantees that exactly one facility is selected and assigned to each location at each time period. Constraint set (4) adds the re-arrangement cost if a facility re-arranges from its location to a new location within two consecutive time periods. Finally, binary restrictions on the decision variables are presented in (5) and (6).
3. Encoding Scheme
Let’s consider a DFLP instance with 6 facilities and 3 time periods (T = 1, 2, 3) as depicted in Figure 1. Those numbers highlighted with bold fonts represent the facilities, and the numbers with red fonts denote the locations. For instance, in first time period, facilities 3, 4, 6, 5, 2, 1 are assigned to locations 1, 2, 3, 4, 5, and 6 respectively. By considering two consecutive time periods 1 and 2, we can see that the locations of facilities 4 and 6 are changed. In fact, the facility 4 from location 2 at time period 1 is moved to location 3 at time period 2, and facility 6 from location 3 at time period 1 is moved to location 2 at time period 2. So the re-arrangement cost needs to be considered due to those re-arrangements.
The solution to this specific instance can be represented by a vector with size of (1 × 18) as represented in Figure 2.
In general, the solution of DFLP problem with N facilities and T time periods can be represented as in Figure 3.

Figure 1. A DFLP instance with six facilities and three time periods.

Figure 2. A solution representation of a DFLP instance with six facilities and three time periods.

Figure 3. Solution representation for DFLP problem with N departments and 
4. Principles of GA
GA is a stochastic optimization technique which is inspired from the biology and evolution process. GA starts with a set of solutions, generated either randomly or using a given heuristicis referred to as the population, and each individual in the population is called a chromosome. The size of the initial population depends on the complexity of problem. A GA with a smaller population is faster but the same time the risk of premature convergence increases. Once the initial population has been generated, the chromosomes are then evaluated by means of fitness function. Parent chromosomes are then selected based on their fitness values to generate new chromosome (child). There are different techniques for selecting parent chromosomes such as roulette wheel selection, tournament selection, and reward-based selection; however the roulette wheel selection is the most commonly used technique. In roulette wheel selection technique [30] , a proportion of the wheel is assigned to each chromosome based on its fitness value. The chromosomes with larger proportion are more likely to be selected. The parent chromosomes are combined using crossover operator to create new chromosomes. New chromosomes are then subjected to random mutation. The purpose of mutation operation is to expand the search directions and prevent the premature convergence. After completing the mutation process, the fitness of new chromosomes is evaluated and crossover and mutation operations start all over. Elitist selection is used to carry better chromosomes from the current generation over to the next generation. Elitist selection may improve the performance of GA but at the same time may results in premature convergence. The evaluation process is repeated until a predetermined condition has been satisfied. The genetic operators used in this context are described as follows:
・ Single point crossover
The proposed single point crossover shame applied in this paper works with single parent instead of two parents. This way of crossover produces feasible offspring and there is no need of checking for solution feasibility. It is also easier to implement. Following are the steps of the proposed single crossover point.
1) Select a parent 
2) Select a time period randomly t, such that
3) Select a random number n, such that
4) If 

5) Facilities from n to N in parent 


6) Similarly, facilities from 1 to (



An illustrative example of single point crossover is depicted in Figure 4.
・ Two exchange (swap) mutation
A cyclic order mutation scheme applied in this paper to modify the locations of facilities in a cyclic order as represented in Figure 5. The following steps are given below:
1) Generate a random time period T such that
2) Choose two facilities 
3) Swap facilities 

5. Variable Neighborhood Search
Variable neighborhood search (VNS) is a recent stochastic local search algorithm proposed by Mladenovic and Hansen [31] . Then main idea behind the VNS is to sequentially explore a set of pre-defined neighborhoods to promote a better solution. The VNS benefits from two important aspects; 1) a local optimal of a neighborhood is not essentially the same as a local optimal of another neighborhood structure, 2) A global optimal is the local optimal of all neighborhood structures. The VNS consists of three major steps; shaking, local search and move.

Figure 4. Illustration of single point crossover operator.

Figure 5. Two exchanges operator.
To begin with the VNS, we need to define a set of neighborhood structure 









Local Searches
Different types of neighborhood structure can be used for the VNS. However, we used three neighborhoods; two exchanges


・ Two exchanges 
The two exchange neighborhood structure used in the VNS is functionally same as two exchange (swap) mutation addressed in Section 4.
・ Insertion 
Step 1: Generate a random time period t such that
Step 2: For the selected time period t, choose two facilities 

Step 3: If a < b, then insert facility 



Example 3: Considering the same instance, the first time period is randomly selected. According to Figure 7(a), the first randomly selected facility is 4 and its corresponding position is 2 (a = 2), and the second randomly selected facility is 5 and its corresponding position is 5 (b = 5). Since 
Insertion operation is depicted in Figure 7(b) when
・ Three exchanges 
Step 1: Generate a random time period t such that
Step 2: For the selected time period t, choose three facilities 
Step 3: Exchange facility 





Example 2: Consider example above, three facilities 4, 2 and 6 are randomly selected, then exchange facility

Figure 6. Template pseudo code of VNS algorithm.

Figure 7. (a) Insertion operation when

4 with facility 2, facility 2 with facility 6 and finally facility 6 with facility 2, as shown in Figure 8.
Note that the size of neighborhood 





A variety of stopping criteria can be used to terminate the running of VNS, such as maximum allowed elapsed time, maximum number of iterations, etc. In this paper, the VNS continues for the number of iterations since the last improvement reaches at the given maximum of
6. Proposed Hybrid Approach
With study of recent works on hybrid metaheurisitcs, it has found that hybrid VNS has dramatically effect on balancing between exploitation and exploration in combinatorial optimization problems [32] -[34] . The proposed hybrid GA-VNS consists in strong cooperation of GA and VNS for the entire course of the algorithm. In each iteration, we split the population into two parts. The splitted parts are evolved using GA and VNS and are then merged together in the updated population and form a new population. Finally, elitism is applied to keep the highest scoring of strings for the next iteration. Similarly, this procedure continues for the next iterations until a stopping criterion is met. The developed flowchart of proposed GA-VNS is exhibited in Figure 9.
The main properties of the hybrid GA-VNS are as follows:
Property 1: Generating the random initial solution.
The hybrid approach begins with a population produced randomly.
Property 2: Diversification using GA

Figure 8. Three exchanges operation.

Figure 9. The developed flowchart of proposed GA-VNS.
It is proven that GA is high capable of shuffling the solution space to prevent search stagnation, but the same time fails to intensify the search toward promising regions of the search space. Nevertheless, hybridization of GA with some suitable local search techniques may overcome the shortcoming feature of each individual algorithm.
Property 3: Intensification using VNS local search.
The concept borrowed by the GA-VNS is that utilizing different neighborhood structures could prevent of getting trapped into local optimal and could also promotes expanding the search scope.
7. Parameters Setting
The driving parameter of proposed hybrid GA-VNS is hybridizing coefficient (HC). HC parameter addresses the percentage of population that is assigned to GA. The proposed hybrid with HC = 1 will be converted to pure GA. It means that the whole population will be evolved with GA, while HC = 0 will be resulted in pure VNS. To take the advantages of features of both GA-VNS, it is clear that HC must be set to some value between 0 and 1 (

where 




8. Experimental Results
To compare the efficiency of the proposed algorithm against some existing algorithms; SAI, SAII [1] , and hybrid ACO [8] , we implemented it in MATLAB 7.8.0.347 (R2009a) and run on a PC with six-core processor 3.30 GHz and 6 GB of RAM. Due to stochastic characteristics of hybrid GA-VNS, five independent replications were run over each problem.
As it can be seen from Table 2, the GA-VNS algorithm obtained the same solution as SAI, SAII, and hybrid ACO for

where 

It is necessary to analyze the computational costs of GA-VNS against the other algorithms but it is hard to have a fair comparison due to utilizing different operating systems, programming procedure, and etc. However, the average CPU time for problem P02 with six facilities, 5 time periods and problem P17 with 15 facilities and 5 time periods were 876 s and 1795 s respectively.
Table 2. Comparison of computational results.

Figure 10. Means plot and 95% LSD for RPD.
9. Conclusion
In this paper, a new hybrid GA-VNS was introduced to deal with the DFLP. In the proposed hybrid algorithm, the population was splitted into two parts; one part was assigned into the GA and the other part was assigned to the VNS. The percentage of splitting population was adjusted by a parameter called hybridizing coefficient (HC) through the course of run. Extensive computational experiments were performed to identify the most suitable parameters setting. The performance of the GA-VNS was compared against SAI, SAII, and hybrid ACO in terms of the quality of solutions. The results reveal that the hybrid GA-VNS gives good or even better solutions in most of the cases.
Cite this paper
Md SanuwarUddin, (2015) Hybrid Genetic Algorithm and Variable Neighborhood Search for Dynamic Facility Layout Problem. Open Journal of Optimization,04,156-167. doi: 10.4236/ojop.2015.44015
References
- 1. McKendall Jr., A.R., Shang, J. and Kuppusamy, S. (2006) Simulated Annealing Heuristics for the Dynamic Facility Layout Problem. Computer and Operations Research, 33, 2431-2444.
http://dx.doi.org/10.1016/j.cor.2005.02.021 - 2. Rosenblatt, M.J. (1986) The Dynamic of Plant Layout. Management Science, 32, 76-86.
http://dx.doi.org/10.1287/mnsc.32.1.76 - 3. Lacksonen, T.A. and Enscore, E.E. (1993) Quadratic Assignment Algorithms for the Dynamic Layout Problem. International Journal of Production Research, 31, 503-517.
http://dx.doi.org/10.1080/00207549308956741 - 4. Baykasoglu, A. and Gindy, N.N.Z. (2001) A Simulated Annealing Algorithm for Dynamic Facility Layout Problem. Computers & Operations Research, 28, 1403-1426.
http://dx.doi.org/10.1016/S0305-0548(00)00049-6 - 5. Balakrishnan, J., Cheng, C.H., Conway, D.G. and Lau, C.M. (2003) A Hybrid Genetic Algorithm for the Dynamic Plant Layout Problem. International Journal of Production Economics, 86, 107-120.
http://dx.doi.org/10.1016/S0925-5273(03)00027-6 - 6. Dunker, T., Radons, G. and Westkamper, E. (2005) Combining Evolutionary and Dynamic Programming for Solving a Dynamic Facility Layout Problem. European Journal of Operational Research, 165, 55-69.
http://dx.doi.org/10.1016/j.ejor.2003.01.002 - 7. Dunker, T., Radons, G. and Westkamper, E. (2003) A Coevolutionary Algorithm for a Facility Layout Problem. International Journal of Production Research, 41, 3479-5300.
http://dx.doi.org/10.1080/0020754031000118125 - 8. McKendall Jr., A.R. and Shang, J. (2006) Hybrid Ant Systems for the Dynamic Facility Layout Problem. Computers and Operations Research, 33, 790-803.
http://dx.doi.org/10.1016/j.cor.2004.08.008 - 9. McKendall Jr., A.R. and Hakobyan, A. (2010) Heuristics for the Dynamic Facility Layout Problem with Unequal-Area Departments. European Journal of Operational Research, 201, 171-182.
http://dx.doi.org/10.1016/j.ejor.2009.02.028 - 10. Chen, G.Y.-H. (2013) A New Data Structure of Solution Representation in Hybrid Ant Colony Optimization for Large Dynamic Facility Layout Problems. International Journal of Production Economics, 142, 362-371.
http://dx.doi.org/10.1016/j.ijpe.2012.12.012 - 11. Guan, J. and Lin, G. (2016) Hybridizing Variable Neighborhood Search with Ant Colony Optimization for Solving the Single Row Facility Layout Problem. European Journal of Operational Research, 248, 899-909.
http://dx.doi.org/10.1016/j.ejor.2015.08.014 - 12. Baykasoglu, A., Dereli, T. and Sabuncu, I. (2006) An Ant Colony Algorithm for Solving Budget Constrained and Unconstrained Dynamic Facility Layout Problems. Omega, 34, 385-396.
http://dx.doi.org/10.1016/j.omega.2004.12.001 - 13. Sahin, R., Ertogral, K. and Turkbey, O. (2010) A Simulated Annealing for the Dynamic Layout Problem with Budget Constraint. Computers and Industrial Engineering, 59, 308-313.
http://dx.doi.org/10.1016/j.cie.2010.04.013 - 14. Ulutas, B.H. and Kulturel-Konak, S. (2012) An Artificial Immune System Based Algorithm to Solve Unequal Area Facility Layout Problem. Expert Systems with Applications, 39, 5384-5395.
http://dx.doi.org/10.1016/j.eswa.2011.11.046 - 15. Komarudin and Wong, K.W. (2010) Applying Ant System for Solving Unequal Area Facility Layout Problems. European Journal of Operational Research, 202, 730-746.
http://dx.doi.org/10.1016/j.ejor.2009.06.016 - 16. Ripon, K.S.N., Glette, K., Khan, K.N., Hovin, M. and Torresen, J. (2013) Adaptive Variable Neighborhood Search for Solving Multi-Objective Facility Layout Problems with Unequal Area Facilities. Swarm and Evolutionary Computation, 8, 1-12.
http://dx.doi.org/10.1016/j.swevo.2012.07.003 - 17. Kulturel-Konak, S. (2012) A Linear Programming Embedded Probabilistic Tabu Search for the Unequal-Area Facility Problem with Flexible Bays. European Journal of Operational Research, 223, 614-625.
http://dx.doi.org/10.1016/j.ejor.2012.07.019 - 18. Hosseini, S., Al Khaled, A. and Vadlamani, S. (2014) Hybrid Imperialist Competitive Algorithm, Variables Neighborhood Search, and Simulated Annealing for Dynamic Facility Layout Problem. Neural Computing and Applications, 25, 1871-1885.
http://dx.doi.org/10.1007/s00521-014-1678-x - 19. Hosseini, S. and Al Khaled, A. (2014) A Survey on the Imperialist Competitive Algorithm Metaheuristic: Implementation in Engineering Domain and Directions for Future Research. Applied Soft Computing, 24, 1078-1094.
http://dx.doi.org/10.1016/j.asoc.2014.08.024 - 20. Vadlamani, S. and Hosseini, S. (2014) A Novel Heuristic Approach for Solving Aircraft Landing Problem with Single Runway. Journal of Air Transport Management, 40, 144-148.
http://dx.doi.org/10.1016/j.jairtraman.2014.06.009 - 21. Al Khaled, A. and Hosseini, S. (2015) Fuzzy Adaptive Imperialist Competitive Algorithm for Global Optimization. Neural Computing and Applications, 26, 813-825.
http://dx.doi.org/10.1007/s00521-014-1752-4 - 22. Hosseini, S., Barker, K. and Ramirez-Marquez, J.E. (2016) A Review of Definitions and Measures of System Resilience. Reliability Engineering and System Safety, 145, 47-61.
http://dx.doi.org/10.1016/j.ress.2015.08.006 - 23. Hosseini, S., Khaled, A. and Jin, M. (2012) Solving Euclidean Minimal Spanning Tree Problem Using a New Meta-Heuristic Competitive Algorithm (ICA). 2012 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Hong Kong, 10-13 December 2012, 176-181.
http://dx.doi.org/10.1109/ieem.2012.6837725 - 24. Khaled, A., Jin, M., Clarke, D.B. and Hoque, M.A. (2015) Train Design and Routing Optimization for Evaluating Criticality of Freight Railroad Infrastructures. Transportation Research Part B: Methodological, 71, 71-84.
http://dx.doi.org/10.1016/j.trb.2014.10.002 - 25. Mamun, A.A., Khaled, A.A., Ali, S.M. and Chowdhury, M.M. (2012) A Heuristic Approach for Balancing Mixed-Model Assembly Line of Type I Using Genetic Algorithm. International Journal of Production Research, 50, 5106-5116.
http://dx.doi.org/10.1080/00207543.2011.643830 - 26. Khaled, A.A., Kumar Paul, S., Kumar Chakraborty, R.K. and Ayuby, S. (2011) Selection of Supplier through Different Multi-Criteria Decision Making Techniques. Global Journal of Management and Business Research, 11, 1-13.
- 27. Masud, A.K.M., Khaled, A.A., Jannat, S., Khan, A.K.M.S.A. and Islam, K.J. (2007) Total Productive Maintenance in RMG Sector A Case Study: Burlington Limited, Bangladesh. Journal of Mechanical Engineering, 37, 62-65.
- 28. Khaled, A.A., Jin, M., Clarke, D.B. and Hoque, M.A. (2013) Determination of Criticality of Freight Railroad Infrastructure Based on Flow Optimization under Heavy Congestion. Transportation Research Board 92nd Annual Meeting, Washington DC, 13-17 January 2013, Paper No. 13-1679.
- 29. Khaled, A.A., Masud, A.K.M., Chowdhury, S.C., Jannat, S. and Obayedullah, M. (2010) Effect of Fiber Diameter Waviness and Wavelength Ratio on the Effective Tensile Elastic Modulus of Carbon Nanotube-Based Polymer Composites. Advanced Material Research, 83, 473-480.
- 30. Burun, E., Erfidan, T. and Ugrum, S. (2006) Improved Power Factor in a Low-Cost PWM Single Phase Inverter Using Genetic Algorithms. Energy Conversion and Management, 47, 1597-1609.
http://dx.doi.org/10.1016/j.enconman.2005.08.010 - 31. Mladenovic, M. and Hansen, P. (1997) Variable Neighborhood Search. Computers and Operations Research, 24, 1097-1100.
http://dx.doi.org/10.1016/S0305-0548(97)00031-2 - 32. Coelho, I.M., Munhoz, P.L.A., haddad, M.N., Souza, M.J.F. and Ochi, L.S. (2012) A Hybrid Heuristic Based on General Variable Neighborhood Search for the Single Vehicle Routing Problem with Deliveries and Selective Pickups. Electronic Notes in Discrete Mathematics, 39, 99-106.
http://dx.doi.org/10.1016/j.endm.2012.10.014 - 33. Ultas, B. and Islier, A.A. (2015) Dynamic Facility Layout Problem in Footwear Industry. Journal of Manufacturing Systems, 36, 55-61.
http://dx.doi.org/10.1016/j.jmsy.2015.03.004 - 34. Selvi, S. and Manimegalai, D. (2015) Multiobjective Variable Neighborhood Search Algorithm for Scheduling Independent Jobs on Computational Grid. Egyptian Informatics Journal, 16, 199-212.
http://dx.doi.org/10.1016/j.eij.2015.06.001



