Received 8 September 2014; revised 16 October 2014; accepted 12 November 2014

ABSTRACT

This paper is an attempt to work out a compromise allocation to construct combined ratio estimates under multivariate double sampling design in presence of non-response when the population mean of the auxiliary variable is unknown. The problem has been formulated as a multi-ob- jective integer non-linear programming problem. Two solution procedures are developed using goal programming and fuzzy programming techniques. A numerical example is also worked out to illustrate the computational details. A comparison of the two methods is also carried out.

Keywords:

Multivariate Stratified Sampling, Compromise Allocation, Non-Response, Double Sampling Goal Programming, Fuzzy Programming

1. Introduction

Often in sample surveys the main variable is highly correlated to another variable called an auxiliary variable and the data on auxiliary variable are either available or can be easily obtained. In this situation to obtain the estimate of the parameters regarding the main variable the auxiliary information can be used to enhance the precision of the estimate. Ratio and Regression Methods and double sampling technique are some examples. When data are collected on the sampled units of the main variable due to one or the other reason, data for all the selected units cannot be obtained. This result is an incomplete and less informative sample. This phenomenon is termed as “non response”. [1] is the first one to consider this problem. Furthermore, when auxiliary parameters are unknown, they can be estimated from a preliminary large sample. Then a second sample is obtained in which the main and auxiliary, both the variables are measured. Often a second sample is a subsample of the first. In such cases only the main variable is to be measured in the second sample. This technique is called “Double Sampling” or “Two Phase Sampling”, [2] - [11] are some who used the auxiliary information in sample surveys. [10] has worked on the problem in which ratio estimator has been considered for population mean under double sampling in presence of non-response for a univariate population.

In the present paper, we considered combined ratio estimators of the population means of a multivariate stratified population using double sampling in presence of non-response. Compromise allocations at first and second phase of double sampling are obtained by formulating the problems as multi-objective integer non-linear programming problems. Solution procedures are developed by using goal programming and fuzzy programming techniques. A numerical example is also worked out to illustrate the computational details. A comparison of the two methods is also carried out.

When auxiliary information is available, the use of Ratio method of estimation is well known in univariate stratified sampling. Formulae are also available to work out optimum allocations to various strata [12] . In multivariate case finding an allocation that gives optimum results for all the characteristics is not possible due to the conflicting nature of the characteristics. Compromise allocation is used in such situations. Furthermore, if the problem of non-response is also there, the situation becomes more complicated. The paper is structured as below:

In Section 2 of the manuscript combined ratio estimates for the population means of the “p” characteristics in presence of non-response using double sampling are constructed. Section 3 formulates the problem of obtaining compromise allocations for phase-I and phase-II of the double sampling as an integer nonlinear programming problem (INLPP). Sections 4 and 5 show that how these INLPP’s can be transformed to apply the Goal Programming Technique (GPT) and the Fuzzy Programming Technique (FPT) to solve the transformed problems. Section 6 provides an application of the techniques through a numerical data. In the last Section 8 gives the conclusion and the future work trend for interested readers.

2. The Combined Ratio Estimate in Multivariate Stratified Double Sampling Design in Presence of Non-Response

Consider a multivariate stratified population of size 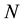with 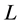non-overlapping strata of sizes 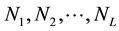with. Let characteristics be defined on each unit of the population. If are not

known in advance then the strata weights also remain unknown. In such situation double sampling technique may be used to estimate the unknown strata weights. For this a large preliminary simple random sample of size is obtained at the first phase of the double sampling, treating the population as unstratified. The number of sampled units 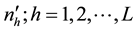falling in each stratum is recorded. The quantity will give an unbiased estimate of. Simple random subsamples, without replacement of sizes 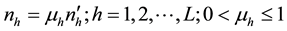are then drawn out of from each stratum for values of 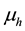chosen in advance.

For the characteristics and the stratum denote by

the value of the population (sample) unit of the main variable.

the value of the population (sample) units of the auxiliary variable.

and the stratum mean and the sample mean respectively for the main variable.

and denote the same values for the auxiliary variable.

In double sampling for stratification the combined ratio estimate of the population mean of the characteristics is given as

(1)

where “CR” and “DS” stand for “combined ratio” and “double sampling” respectively.

Further,

The sampling variance of is

(2)

in (2) is defined as

(3)

where are true population ratios given as

are the stratum variances of the characteristics in the stratum for main variable and auxiliary variables respectively and are the stratum co-variances of the characteristics in the

stratum for

In the presence of non-response, let out of the units units respond at the first call and units constitute the non-respondents group. Using [1] , a subsample of size out of

is drawn and interviewed with extra efforts. Where are fixed in advance.

An combined ratio estimate of may be given as

(4)

where

, are the sample mean of the ratio estimates for respondents (based on units) and non-respon- dents group (based on units) respectively.

Using the results presented in [12] ―Sections 5A.2, 12.9 and 13.6 we get in presence of non-re- sponse as

(5)

where,

are the stratum variances of the characteristics of the non-respondents in the stratum for main variable and auxiliary variable respectively. is the stratum co-variances of the characteristics of the non-respondents in the stratum [11] .

The total cost of the survey may be given

(6)

where,

is the per unit cost of getting information from the preliminary sample.

is the per unit cost of of making the first attempt (Phase I).

is the per unit cost of processing and analyzing the result of all the characteristics on the respondents units in the stratum at Phase I.

is the per unit cost of measuring and processing the result of all the characteristics on the subsampled units from non-respondents group in the stratum at Phase II.

Since is not known until the first attempt is made, the quantity may be used as its expected value. The total expected cost of the survey is then given as

(7)

3. Formulation of the Problem

In Phase I, we obtain the sample size in each stratum by minimizing variance given in (5) for fixed cost given in (7). At Phase II subsample size from non-respondents group has been obtained by minimizing the sampling variance in (5) for given cost in (7).

3.1. Formulation of the Problem at Phase I

Expression (5) can be expressed as

(8)

where the terms independent of are ignored

(9)

The cost constraint (7) becomes

(10)

where

Thus the multi-objective formulation of the problem at Phase I becomes

(11)

(see [11] ).

3.2. Formulation of the Problem for Phase II

Ignoring the term independent from in (5), substituting and for expression (5) can be written as

(12)

where

(13)

The cost constraint becomes

where

(14)

Then the multi-objective formulation of the problem at Phase II becomes

(15)

4. Formulation as a Goal Programming Problem

4.1. Phase I

Let be the optimal value of under optimum allocation for the characteristics obtained by solving the following integer non-linear programming for all the characteristics separately.

(16)

Further let

(17)

denote the variance under the compromise allocation, where are to be worked out.

Obviously and will give the increase in the variances due to not using the individual optimum allocation for characteristics.

Let denote the tolerance limit specified for.

We have

or

or (18)

A suitable compromise criterion to work out a compromise allocation at phase-I will then be to minimize the sum of deviations. Therefore the Goal Programming problem at phase-I may be given as

(19)

(See [13] ). Where are the goal variables.

The goal is now to minimize the sum of deviations from the respective optimum variances.

4.2. Phase II

Similarly, at phase II Goal Programming formulation of the problem (15) will be

(20)

5. Formulation as a Fuzzy Programming Problem

5.1. Phase I

To obtain Fuzzy solution we first compute maximum value and minimum value for each characteristic. where

(21)

where denote the optimum allocation for the characteristics and the maximum and minimum are for all, among their values for a particular.

The difference of the maximum value and minimum values are denoted by .

The Fuzzy Programming Problem (FPP) corresponding to the (11) at phase I is given by the following NLPP

(22)

where is the decision variable representing the worst deviation level.

5.2. Phase II

Similarly, the Fuzzy Programming Problem corresponding to the (15) at phase II is given by the following NLPP

(23)

where is the decision variable representing the worst deviation level.

The NLPPs may be solved by using the optimization software [14] . For further information about LINGO one may visit the site: http://www.lindo.com.

6. A Numerical Example

The data in Table 1 use are from [15] . A population of size is divided into four strata. Two characteristic and are defined on each unit of the population. The values of and are used as the auxiliary information corresponding on the main variable and The authors have assumed the values for and Table 2 shows the other data. Each stratum is divided into respondents and non- respondents as shown in Table 2.

It is assumed that and are known and the preliminary sample size.

In the last column of Table 2, is for respondents group and is for non-respondents group.

The total cost for the survey is taken as 3000 units. Out of which 750 units are for the preliminary sample, 1900 units are for phase-I and 350 units are for phase-II.

Using estimated values of strata weights the values of are obtained as

6.1. Computation of Compromise Allocation Using Goal Programming Technique (GPT)

6.1.1. Individual Optimum Allocation (Phase I)

Using data from Table 1 and Table 2, we compute the individual optimum allocation for each characteristic by using NLPP (11) will be the solution to:

For

Using optimization software LINGO we get the optimal solution as

For

Using optimization software LINGO we get the optimal solution as

6.1.2. Compromise Solution Using Goal Programming (Phase I)

Using data from Table 1 and Table 2 the Goal Programming Problem (19) can be formulated as

Using optimization software LINGO we get the optimal solution as

with and the optimum value of the objective function

6.1.3. Individual Optimum Allocation (Phase II)

As in Section 6.1.1 for the given data the individual optimum allocations for each the two characteristics using NLPP (15) are:

For

For

6.1.4. Compromise Solution Using Goal Programming (Phase II)

For the given data, as in Section 6.1.2 Goal Programming Problem (20) gives the following optimal solution

with and the optimum value of the objective function

6.2. Computations of Compromise Solution Using Fuzzy Programming Technique (FPT)

6.2.1. Compromise Solution Using Fuzzy Programming (Phase I)

To obtain fuzzy solution we first obtained the maximum value and minimum value as given in (21) for each characteristic by using individual optimum allocation worked out in Section 6.1.1

and

After computing the optimum allocation and optimum variances for two characteristics the compromise optimal solution for the above problem can be obtained by solving the given Fuzzy Programming Problem (FPP) of (23)

Using optimization software LINGO we get the optimal solution as

6.2.2. Compromise Solution Using Fuzzy Programming (Phase II)

Similarly, using data from Table 1 and Table 2 the Fuzzy Programming Problem (23) gives the following optimal solution

7. Summary of the Results

In the following results obtained using Goal Programming Technique and Fuzzy Programming Technique are summarized.

8. Conclusions

Table 3 and Table 4 show the values of the variance of the combined ratio estimates of the population means at Phase-I and Phase-II respectively, for the two characteristics. The figures show that both the approaches the Goal Programming Approach and the Fuzzy Programming Approach give almost same results. However, at Phase-I the Goal Programming Approach is slightly more precise in terms of the trace value (See [16] ).

The Goal Programming and Fuzzy Programming technique and some other techniques like Dynamic Programming and Separable Programming can be used to solve a wide variety of mathematical programming problems. These techniques may be of great help in solving multivariate sampling problem also. Like determining

the number of strata, strata boundaries and compromise allocations in multivariate stratified sampling. Little work has been done to solve the above mentioned optimization problems in real life situations. For example when the estimates of the population parameters used in formulating the problems are themselves treated as random variables with assumed or known distributions. In such cases the formulated problems becomes a multivariate stochastic programming. Further, apart from a linear cost function, nonlinear functions may be used that may include travel cost, labour cost, rewards to the respondent and incentives to the investigators etc. Interested researchers may expose these situations.

Acknowledgements

The authors are thankful to the Editor for his valuable remarks and suggestions that helped us a lot in improving the standard of the paper. This research work is partially supported by the UGC grant of Emeritus Fellowship to the author Mohammed Jameel Ahsan for which he is grateful to UGC.

References