Graphene
Vol.05 No.01(2016), Article ID:63186,10 pages
10.4236/graphene.2016.51003
Morphological Characterization of Graphene Flake Networks Using Minkowski Functionals
Igor Levchenko1, Jinghua Fang2, Kostya (Ken) Ostrikov1,3,4, Ludovico Lorello5, Michael Keidar6
1School of Chemistry, Physics, and Mechanical Engineering, Queensland University of Technology, Brisbane, Australia
2School of Mathematical and Physical Sciences, Faculty of Science, University of Technology Sydney, Ultimo, Australia
3Joint CSIRO―QUT Sustainable Materials and Devices Laboratory, Commonwealth Scientific and Industrial Research Organisation, Lindfield, Australia
4Beijing National Laboratory for Molecular Sciences (BNLMS), College of Chemistry and Molecular Engineering, Peking University, Beijing, China
5Materials Science Department, University of Milano-Bicocca, Milano, Italy
6George Washington University, Washington DC, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 January 2016; accepted 26 January 2016; published 29 January 2016
ABSTRACT
Two Minkowski functionals were tested in the capacity of morphological descriptors to quantitatively compare the arrays of vertically-aligned graphene flakes grown on smooth and nanoporous alumina and silica surfaces. Specifically, the Euler-Poincaré characteristic and fractal dimension graphs were used to characterize the degree of connectivity and order in the systems, i.e. in the graphene flake patterns of petal-like and tree-like morphologies on solid substrates, and mesh- like patterns (networks) grown on nanoporous alumina treated in low-temperature inductively- coupled plasma. It was found that the Minkowski functionals return higher connectivity and fractal dimension numbers for the graphene flakepatterns with more complex morphologies, and indeed can be used as morphological descriptors to differentiate among various configurations of vertically-aligned graphene flakes grown on surfaces.
Keywords:
Graphene Flakes, Minkowski Functionals, Euler-Poincaré Characteristic, Connectivity

1. Introduction
Morphological parameters of the networks of nanostructures on surfaces and in nanocomposites directly influence many important characteristics of the whole structure such as electric resistance [1] , thermal conductivity [2] , percolation threshold [3] , mechanical strength [4] , optical [5] [6] , electronic [7] and magnetic [8] [9] properties. Among others, networks of vertically-aligned few-layered graphene flakes [10] and graphene-polymer nanocomposites [11] attract a special interest due to extraordinary mechanical, electrical, magnetic and other properties of these systems [12] -[14] , and morphological features of such networks also significantly affect their properties. It should be noted that the vertically-aligned few-layered graphene flakes are under extensive investigations nowadays and many other terms could be used in the literature to address these kind of nanostructures, such as vertically aligned carbon nanowalls [15] , vertically oriented graphene sheets [16] , vertically aligned multilayer graphenes [17] and vertically aligned graphene layers [18] . Nevertheless, we will call them vertically- aligned few-layered graphene flakes (FLGF) for simplicity.
Typically, arrays of FLGF are formed using low-temperature plasma-based processes [19] , e.g. based on the inductively-coupled plasma (ICP) technique [20] . Depending on the specific process parameters (e.g., substrate temperature, discharge power and electron energy) and used materials, the physical, mechanical and structural characteristics of FLGF can vary in a wide range [21] . Arc discharges can be used for the production of free- standing (i.e., not attached to surface) graphene flakes, which could be further transferred to the surface [22] . Plasma generated by other types of discharges (e.g. direct current cylindrical magnetron [23] ) also could be promising for the graphene flakes fabrication.
Apart from fabrication, graphene characterization represent a separate problem and many sophisticated methods (such as Raman spectroscopy, scanning electron and transmitting electron microscopy, etc.) were developed to measure electrical, mechanical, magnetic, thermodynamic and other properties of graphenes; the reader can refer to numerous review papers [24] to find detailed information on any specific characterization technology. However, researchers still suffer from the lack of simple, informative, and commonly accepted methods and parameters to quantify the graphene network architecture and morphological properties, and eventually correlate them with the physical properties of the whole network. As a result, the attempts to describe the morphological characteristics of the patterns formed by graphene flakes of similar structure but at different configuration could represent a problem.
Minkowski functionals are statistical measures used to characterize geometrical structure and morphology of a system composed of many objects irregularly distributed in the two- and three-dimensional space. These measures were successfully used to relate the structural characteristic with the physical parameters of such systems. For example, Minkowski functionals were capable of predicting fluid flows in porous substrates [25] , calculation of percolation thresholds [26] , estimation of mechanical and transport properties [27] [28] , as well as permeability [29] and strength [30] of complex systems with stochastically distributed objects. Moreover, the Minkowski functional formalism could be extended to the patterns of other material types and various dimensionalities, and specifically, to large arrays of metal oxide nanowires such as, e.g., α-Fe2O3, ZnO and niobium pentoxide Nb2O5 [31] [32] . Minkowski functional may also be used to characterize morphological features of the MoO3nanosheetpatterns [33] , as well as surface roughness of interfaces capable of supporting electromagnetic wave excitations [34] .
In this work we have used the two functionals, namely the Minkowski connectivity (the Euler-Poincaré characteristic) and fractal dimension (FD) to quantify the degree of connectivity and randomness in several patterns of vertically-aligned few-layered graphene flakes grown on solid and nanoporous surfaces. Specifically, we have examined the graphene flake patterns of petal-like and tree-like morphologies grown on solid substrates, and mesh-like arrays grown on nanoporous alumina (Al2O3) membranes after various treatments. We have demonstrated that the Minkowski connectivity and fractal dimension essentially depend on the morphological features of graphene patterns, and thus could be used as morphological descriptors to differentiate between various graphene flakes configurations on surfaces and hence, obtain a quantitative measure to correlate the geometrical configuration of the pattern with its physical properties.
2. Experiment and Analysis
2.1. Fabrication of Graphene Flakes on Nanoporous Alumina and Solid Silica
For the graphene formation on nanoporous surfaces, the alumina (Al2O3) membrane was prepared by a simple and convenient liquid anodization technique [35] . The Al foil (thickness of 300 μm, sample diameter 10 mm)wasanodized using the direct current voltage of 50 V in the oxalic acid (Figure 1) to obtain pore size of 200 nm. The samples were then subjected to various types of post-treatment to obtain various morphologies of graphene flakes on the treated surface. Specifically, one sample were processed in ICP plasma (Ar gas, RF power 750 W, 2 min), second one was coated with Au (30 nm), the others were treated with Au, CO, and Pd ions by immersing them for 24 hours into KAu(CN)2, CoSO4, and PdCl2 solutions, respectively, and then drying in N2. After that, the mesh-like network of vertically-aligned graphene flakes was grown on all samples in ICP reactor (CH4/Ar/H2 ratio was 2:1:1, pressure of 3.0 Pa, power 850 W, process time 6 min). Samples were characterized by scanning electron microscope (SEM) technique using field-emission scanning electron microscopy (FE-SEM Zeiss Auriga), with the electron beam energy of 1 to 5 keV and InLens secondary electron detector. The structure of the graphene flakes was also studied using the transmission electron microscopy technique by the microscope JOEL 2100 operated at electron beam energy of 200 keV. The SEM images were then used for the statistical analysis. More details on this process and properties of the nanoporous membranes can be found elsewhere [36] . SEM images and three-dimensional reconstruction of several mesh-like structures are shown in Figure 2 and Figure 3.
Figure 1. Schematics of graphene flake network fabrication on nanoporous alumina membranes. Al foil (a) is subjected to electrochemical processing (b) to form the nanoporous membrane (c), which is then post-processed in plasma or chemical reagents (d). Few-layered graphene flakes are then nucleated and grow on the treated surface (e), eventually forming a complex pattern of vertically-aligned nanowalls (f).
Figure 2. SEM images of the mesh-like network of few-layer vertically-aligned graphene flakes grown on nanoporous alumina covered with 30 nm of sputtered gold (a) and processed with Co+ ions in solution (b). Network morphologies are significantly different and apparently cannot be visually compared and assessed.
Figure 3. Three-dimensional reconstruction of the nanoflake relief for the vertically-aligned networks of few-layer graphene flakes grown on nanoporous alumina membranes with various types of post-processing. (a) Reference sample (nanoflakes grown on the surface of as-prepared alumina membrane); (b) nanoflakes grown on alumina membrane sputter-coated with 30-nm gold film; nanoflakes grown on alumina processed in solution with gold ions (c), palladium ions (d), Co ions (e) and Ar plasma (f). Sample size is 4 μm for all cases. Apparently, the network morphologies are significantly different and cannot be visually compared and assessed.
In the second experiment, the FLGF networks were grown on thick Si(100) substrates covered with a 500 nm silica (SO2) layer. The samples were also treated with the low-temperature Ar plasma, and then the flakes were grown in the ICP reactor under similar conditions, without the use of any catalysts and external substrate heating. During the treatment, substrates were negatively biased and heated by the plasma to 700 - 750 K. So-called petal-like and tree-like graphene flake networks were formed in this experiment, with the petal-like structure grown at lower CH4 and higher H4 contents on the surfaces biased with −50 V potential during processing in Ag plasma, whereas the tree-like networks were grown at higher CH4 and lower H4 contents on the surfaces biased with −100 V potential. More details on the process and results can be found elsewhere [37] [38] . Further characterization has shown that increased process voltage (−100 V) resulted in the fragmentation of a silica layer and formation of SiO2 islands, which led to the formation of tree-like network, whereas petal-like structures were formed on the smooth silica surface.SEM images and 3D reconstruction of the tree-like and petal-like structures are shown in Figure 4.
2.2. Minkowski Functionals for Graphene Flake Networks
Minkowski connectivity distribution (Euler-Poincaré characteristic ξ) is one of morphological descriptors which
Figure 4. Minkowski connectivities (Euler-Poincaré characteristic ξ) and fractal dimension ψ curves for the networks of few-layer graphene flakes grown on nanoporous alumina membranes with various types of post-processing. (a) ξ and ψ for the reference sample (nanoflakes grown on the surface of as-prepared alumina membrane); ξ and ψ for networks grown on alumina membrane sputter-coated with 30-nm gold film (b); grown on alumina processed in solution with gold ions (c), palladium ions (d), Co ions (e) and Ar plasma (f). The curves have very different shapes and behaviors, thus demonstrating a high selectivity and sensitivity of this method. In all graphs the upper (Z/Zmax) scale refers to connectivity ξ and lover scale log(1/l) refers to the fractal dimension curve.
was used to characterize various morphologies and geometrical properties of thin films [39] , large nanotube networks [40] , complex networks inlaying the surface such as carbon interconnections [41] and other similar patterns. Specifically, Minkowski connectivity describes the measure of the amount of connections in the pattern by analyzing the relationship of connected and disconnected pixels in an image. In general case ξ is defined [42] :
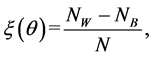 (1)
(1)
where θ is the threshold, i.e. parameter running over the whole interval between the lightest and darkest hints in the image; NW and NB are the numbers of continuous (percolated) clusters of pixels above and below the threshold θ, respectively; and N is the total number of pixels. Apparently, ξ is a characteristic of properties which depend on the interconnection of nanostructures in network, such as percolation threshold, conductivity and others related to the transfer of gas, heat, electrons etc. between the nanostructures [43] .
Fractal dimension is one more morphological descriptor often used to characterize morphological features and degree of order/randomness of the complex arrays and networks [36] . Importantly, fractal dimension can be correlated with the physical properties of the patterns, such as thermal conductivity for porous media [44] , hydraulic conductivity [45] , and complex conductivity [46] . It was also demonstrated that the films with significant fractal character [47] exhibit intense surface-enhanced Raman spectra (SERS) [48] . In classical formulation, the fractal dimension ψ is the limit of logarithmic ratio of the number of self-similar objects N(l) and length scale 1/l, i.e.
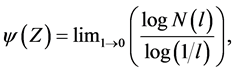 (2)
(2)
where Z is the current height of the network or hint threshold for the image [49] .
Geometrically the fractal dimension ψ can be interpreted as the power of stretched factor k which return the area increase; i.e. if the area was increased by the factor of k, the area increase is δ = kψ. Apparently, for the continued (not fractalized) surface with ψ = 2 this will return δ = 22 = 4, as expected. For the fractalized surface ψ can exceed 2, that is, fractalized surface cannot be considered as flat.
3. Results
Analysis of Minkowski Functionals for Networks on Alumina and Silica
Figure 2 shows the scanning electron microscopy (
Figure 3 illustrates three-dimensional reconstructions of the vertically-aligned network grown on nanoporous alumina with various types of post-processing described in the Fabrication of Graphene Flakes on Nanoporous Alumina and Solid Silica section above. Specifically, Figure 3(a) shows the reference sample which was fabricated by growing the graphene nanoflakes on as-prepared alumina membrane, just washed and dried with a jet of dry nitrogen gas. Figures 3(b)-(f) show the nanoflakes on the surface of alumina membrane sputter-coated with 30-nm gold (b), as well as nanoflakes on alumina processed with gold (c), palladium (d), and Co ions (e) in solutions, and processed with ICPAr plasma (f) under the following conditions: Ar gas flux was 10 sccm, chamber pressure of 2.0 Pa, radio frequency power used to ignite and sustain the plasma was 800 - 1000 W, the samples were treated for 2 - 5 min.
All shown samples have a size of 4 μm. These three-dimensional reconstructions reveal the significant differences in morphology and help to better understand the specific features of the network. Nevertheless, the whole structures apparently cannot be visually compared and assessed.
Minkowski connectivity distribution and fractal dimension curves for all samples were calculated using the Gwyddion© visualization and analysis free software (released by GPL license). The results of the analysis of six samples are presented in Figure 4. Each graph in Figure 4 depicts the Minkowski connectivity curve combined with the fractal dimension curve for a single spacemen. Moreover, mean fractal dimensions were calculated using the three techniques (cube counting, triangulation, and power spectrum methods), and the results are summarized in Table 1. This Table also lists the ψ values for graphene networks grown on solid silica.
Table 1. Mean fractal dimensions for graphene nanoflake networks grown on nanoporous alumina and solid silica.
Figure 5. Three-dimensional reconstruction (a, b), and graphs for Minkowski connectivity (c) and fractal dimensions (d) for the tree-like and petal-like graphene networks grown on solid silica. Apparently, the analysis demonstrates higher connectivity and fractal dimension numbers for the graphene patterns with more complex morphologies, and indeed can be used as morphological descriptors.
It is quite apparent from the analysis of graphs shown in Figure 4 that the Minkowski connectivity ξ and fractal dimension curves for the networks grown on nanoporous alumina membranes with various types of post-processing strongly differ and depend on the network morphology, thus demonstrating a high selectivity, informativity and sensitivity of this method. The highest connectivity numbers (ξ = 10−2) were obtained for the networks grown on deposited gold film, whereas the plasma-processed samples have demonstrated ξ = 3 × 10−3, and the lowest numbers (ξ = 4 × 10−4) characterize the networks processed with gold ions in solution (presumably, due to their low chemical activity). Zero and peak values of the connectivity curves are dispersed in a wide range of nanoflake heights ranging from 0.1 to 0.9, thus evidencing the fact that the predominant connectivity in various networks could be located at quite different distances from the network bottom. The fractal dimension curves also demonstrate higher numbers for more complex shapes.
The 3D appearance and relevant graphs for the petal- and tree-like networks grown on the smooth silica surfaces are shown in Figure 5, which reveals very different (radial for tree-like and enclosed for petal-like structures) morphologies, as seen in Figure 5(a) and Figure 5(c). To better compare these distributions, we have plotted combined connectivity graphs for connectivities and fractal dimensions, Figure 5(b) and Figure 5(d). From these graphs one can see that tree-like sample is characterized by lower connectivity, and this is quite noticeable from the 3D structure where on Figure 5(a) where nanoflakes are mainly not in contact with each other. The fractal dimension graphs on Figure 5(d) also evidence higher degree of randomness for the petal-like network.
4. Summary
We have demonstrated that the Minkowski functionals, namely the connectivity (Euler-Poincaré characteristic) and fractal dimension can be used as morphological descriptors for the complex networks of vertically-aligned few-layergraphene nanoflakes grown on surfaces in the inductively-coupled plasma. The method was validated using the nanoflakes grown on nanoporous alumina and solid (smooth) silica, and high sensitivity demonstrated. Specifically, higher connectivity and fractal dimension numbers were obtained for the patterns with more complex morphologies. More detailed studies will be undertaken to relate the above described functionals, as well as other statistical parameters with the geometrical, morphological, and eventually physical properties of the complex surface-bound graphene patterns.
Acknowledgements
I. L. acknowledges the support from the School of Chemistry, Physics and Mechanical Engineering, Science and Engineering Faculty, Queensland University of Technology. This work was partially supported by the Australian Research Council and CSIRO’s OCE Science Leadership Scheme.
Cite this paper
IgorLevchenko,JinghuaFang,Kostya (Ken)Ostrikov,11,LudovicoLorello,MichaelKeidar, (2016) Morphological Characterization of Graphene Flake Networks Using Minkowski Functionals. Graphene,05,25-34. doi: 10.4236/graphene.2016.51003
References
- 1. Takeuchi, W., Ura, M., Hiramatsu, M., Tokuda, Y., Kano, H. and Hori, M. (2008) Electrical Conduction Control of Carbon Nanowalls. Applied Physics Letters, 92, Article ID: 213103. http://dx.doi.org/10.1063/1.2936850
- 2. Song, W.L., Wang, P., Cao, L., Anderson, A., Meziani, M.J., Farr, A.J. and Sun, Y.P. (2012) Polymer/Boron Nitride Nanocomposite Materials for Superior Thermal Transport Performance. Angewandte Chemie International Edition, 51, 6498-6501. http://dx.doi.org/10.1002/anie.201201689
- 3. Faiella, G., Piscitelli, F., Lavorgna, M., Antonucci, V. and Giordano, M. (2009) Tuning the Insulator to Conductor Transition in a Multiwalled Carbon Nanotubes/Epoxy Composite at Substatistical Percolation Threshold. Applied Physics Letters, 95, Article ID: 153106. http://dx.doi.org/10.1063/1.3242017
- 4. Blackman, B.R.K., Kinloch, A.J., Sohn Lee, J., Taylor, A.C., Agarwal, R., Schueneman, G. and Sprenger, S. (2007) The Fracture and Fatigue Behavior of Nano-Modified Epoxy Polymers. Journal of Materials Science, 42, 7049-7051. http://dx.doi.org/10.1007/s10853-007-1768-6
- 5. Beecroft, L.L. and Ober, C.K. (1997) Nanocomposite Materials for Optical Applications. Chemistry of Materials, 9, 1302-1317. http://dx.doi.org/10.1021/cm960441a
- 6. Kelly, K., Coronado, E., Zhao, L. and Schatz, G.C. (2003) The Optical Properties of Metal Nanoparticles. The Influence of Size, Shape and Dielectric Environment. Journal of Physical Chemistry B, 107, 668-677. http://dx.doi.org/10.1021/jp026731y
- 7. Williams, M.D. and Hess, D.W. (2013) Effect of Growth Morphology on the Electronic Structure of Epitaxial Graphene on SiC. Graphene, 2, 55-59. http://dx.doi.org/10.4236/graphene.2013.21008
- 8. Li, S., Lin, M.M., Toprak, M.S., Kim, D.K. and Muhammed, M. (2010) Nanocomposites of Polymer and Inorganic Nanoparticles for Optical and Magnetic Applications. Nano Reviews, 1, Article ID: 5214. http://dx.doi.org/10.3402/nano.v1i0.5214
- 9. Gass, J., Poddar, P., Almand, J., Srinath, S. and Srikanth, H. (2006) Superparamagnetic Polymer Nanocomposites with Uniform Fe3O4 Nanoparticle Dispersions. Advanced Functional Materials, 16, 71-75. http://dx.doi.org/10.1002/adfm.200500335
- 10. Levchenko, I., Keidar, M., Xu, S., Kersten, H. and Ostrikov, K. (2013) Low-Temperature Plasmas in Carbon Nanostructure Synthesis. Journal of Vacuum Science & Technology B, 31, Article ID: 050801. http://dx.doi.org/10.1116/1.4821635
- 11. Galpaya, D., Wang, M., Liu, M., Motta, N., Waclawik, E. and Yan, C. (2012) Recent Advances in Fabrication and Characterization of Graphene-Polymer Nanocomposites. Graphene, 1, 30-49. http://dx.doi.org/10.4236/graphene.2012.12005
- 12. Soin, N., Roy, S.S., Lim, T.H. and McLaughlin, J.A.D. (2011) Microstructural and Electrochemical Properties of Vertically Aligned Few Layered Graphene (FLG) Nanoflakes and Their Application in Methanol Oxidation. Materials Chemistry and Physics, 129, 1051-1057. http://dx.doi.org/10.1016/j.matchemphys.2011.05.063
- 13. Malesevic, A., Kemps, R., Vanhulsel, A., Chowdhury, M.P., Volodin, A. and van Haesendonck, C. (2008) Field Emission from Vertically Aligned Few-Layer Graphene. Journal of Applied Physics, 104, Article ID: 084301. http://dx.doi.org/10.1063/1.2999636
- 14. Li, J., Cheng, X., Shashurin, A. and Keidar, M. (2012) Review of Electrochemical Capacitors Based on Carbon Nanotubes and Graphene. Graphene, 1, 1-13. http://dx.doi.org/10.4236/graphene.2012.11001
- 15. Hiramatsu, M., Shiji, K., Amano, H. and Hori, M. (2004) Fabrication of Vertically Aligned Carbon Nanowalls Using Capacitively Coupled Plasma-Enhanced Chemical Vapor Deposition Assisted by Hydrogen Radical Injection. Applied Physics Letters, 84, 4708-4710. http://dx.doi.org/10.1063/1.1762702
- 16. Bo, Z., Yu, K., Lu, G., Cui, S., Mao, S. and Chen, J. (2011) Vertically Oriented Graphene Sheets Grown on Metallic Wires for Greener Corona Discharges: Lower Power Consumption and Minimized Ozone Emission. Energy & Environmental Science, 4, 2525-2528. http://dx.doi.org/10.1039/C1EE01140E
- 17. Liang, Q., Yao, X., Wang, W., Liu, Y. and Wong, C.P. (2011) A Three-Dimensional Vertically Aligned Functionalized Multilayer Graphene Architecture: An Approach for Graphene-Based Thermal Interfacial Materials. ACS Nano, 5, 2392-2401. http://dx.doi.org/10.1021/nn200181e
- 18. Guo, F., Mukhopadhyay, A., Sheldon, B.W. and Hurt, R.H. (2011) Vertically Aligned Graphene Layer Arrays from Chromonic Liquid Crystal Precursors. Advanced Materials, 23, 508-513. http://dx.doi.org/10.1002/adma.201003158
- 19. Xu, S., Huang, S.Y., Levchenko, I., Zhou, H.P., Wei, D.Y., Xiao, S.Q., et al. (2011) Highly Efficient Silicon Nanoarray Solar Cells by a Single-Step Plasma-Based Process. Advanced Energy Materials, 1, 373-376. http://dx.doi.org/10.1002/aenm.201100085
- 20. Fang, J., Levchenko, I., Kumar, S., Seo, D. and Ostrikov, K. (2015) Vertically-Aligned Graphene Flakes on Nanoporous Templates: Morphology, Thickness, and Defect Level Control by Pre-Treatment. Science and Technology of Advanced Materials, 15, Article ID: 055009. http://dx.doi.org/10.1088/1468-6996/15/5/055009
- 21. Fang, X., Donahue, J., Shashurin, A. and Keidar, M. (2015) Plasma-Based Graphene Functionalization in Glow Discharge. Graphene, 4, 1-6. http://dx.doi.org/10.4236/graphene.2015.41001
- 22. Volotskova, O., Levchenko, I., Shashurin, A., Raitses, Y., Ostrikov, K. and Keidar, M. (2010) Single-Step Synthesis and Magnetic Separation of Graphene and Carbon Nanotubes in Arc Discharge Plasmas. Nanoscale, 2, 2281-2285. http://dx.doi.org/10.1039/c0nr00416b
- 23. Levchenko, I., Romanov, M. and Keidar, M. (2003) Investigation of a Steady-State Cylindrical Magnetron Discharge for Plasma Immersion Treatment. Journal of Applied Physics, 94, 1408-1413. http://dx.doi.org/10.1063/1.1590054
- 24. Yin, P.T., Shah, S., Chhowalla, M. and Lee, K.-B. (2015) Design, Synthesis, and Characterization of Graphene-Nanoparticle Hybrid Materials for Bioapplications. Chemical Reviews, 115, 2483-2531. http://dx.doi.org/10.1021/cr500537
- 25. Lehmann, P., Berchtold, M., Ahrenholz, B., Toelke, J., Kaestner, A., Krafczyk, M., et al. (2008) Impact of Geometrical Properties on Permeability and Fluid Phase Distribution in Porous Media. Advances in Water Resources, 31, 1188-1204. http://dx.doi.org/10.1016/j.advwatres.2008.01.019
- 26. Rodríguez-Valverde, M.A., Ramón-Torregrosa, P.J. and Cabrerizo-Vílchez, M.A. (2010) Estimation of Percolation Threshold of Acid-Etched Titanium Surfaces Using Minkowski Functionals. In: Méndez-Vilas, A. and Díaz, J., Eds., Microscopy: Science, Technology, Applications and Education, Volume 3, Formatex, Banajoz, 1978-1983.
- 27. Arns, C.H., Knackstedt, M.A. and Mecke, K. (2003) Reconstructing Complex Materials via Effective Grain Shapes. Physical Review Letters, 91, Article ID: 215506. http://dx.doi.org/10.1103/PhysRevLett.91.215506
- 28. Mecke, K. and Arns, C.H. (2005) Fluids in Porous Media: A Morphometric Approach. Journal of Physics: Condensed Matter, 17, S503-S534. http://iopscience.iop.org/article/10.1088/0953-8984/17/9/014/pdf
- 29. Rajaram, H., Ferrand, L.A. and Celia, M.A. (1997) Prediction of Relative Permeabilities for Unconsolidated Soils Using Pore-Scale Network Models. Water Resources Research, 33, 43-52. http://dx.doi.org/10.1029/96WR02841
- 30. Monetti, R.A., Bauer, J., Sidorenko, I., Mueller, D., Rummeny, E.J. and Matsuura, M. (2009) Assessment of the Human Trabecular Bone Structure Using Minkowski Functionals. Proceedings of SPIE, 7262, Article ID: 2620N. http://iopscience.iop.org/article/10.1117/12.811322
- 31. Cvelbar, U. (2011) Towards Large-Scale Plasma-Assisted Synthesis of Nanowires. Journal of Physics D: Applied Physics, 44, 4980-4986. http://dx.doi.org/10.1088/0022-3727/44/17/174014
- 32. Cvelbar, U., Chen, Z.Q., Sunkara, M.K. and Mozetic, M. (2008) Spontaneous Growth of Superstructure α-Fe2O3 Nanowire and Nanobelt Arrays in Reactive Oxygen Plasma. Small, 4, 1610-1614. http://dx.doi.org/10.1002/smll.200800278
- 33. Mariotti, D., Lindström, H., Bose, A.C. and Ostrikov, K.K. (2008) Monoclinic β-MoO3 Nanosheets Produced by Atmospheric Microplasma: Application to Lithium-Ion Batteries. Nanotechnology, 19, Article ID: 495302. http://dx.doi.org/10.1088/0957-4484/19/49/495302
- 34. Azarenkov, N.A. and Ostrikov, K.N. (1999) Surface Magnetoplasma Waves at the Interface between a Plasma-Like Medium and a Metal in the Voigt Geometry. Physics Reports, 308, 333-428. http://dx.doi.org/10.1016/S0370-1573(98)00032-5
- 35. Fang, J., Levchenko, I., Ostrikov, K. and Prawer, S. (2013) Sonochemical Nanoplungers: Crystalline Gold Nanowires by Cavitational Extrusion through Nanoporous Alumina. Journal of Materials Chemistry C, 1, 1727-1731. http://dx.doi.org/10.1039/c2tc00560c
- 36. Fang, J., Aharonovich, I., Levchenko, I., Ostrikov, K., Spizzirri, P.G., Rubanov, S., et al. (2012) Plasma-Enabled Growth of Single-Crystalline SiC/AlsiC Core-Shell Nanowires on Porous Alumina Templates. Crystal Growth and Design, 12, 2917-2922. http://dx.doi.org/10.1021/cg300103a
- 37. Yue, Z., Levchenko, I., Kumar, S., Seo, D., Wang, X., Dou, S., et al. (2013) Large Networks of Vertical Multi-Layer Graphenes with Morphology-Tunable Magnetoresistance. Nanoscale, 5, 9283-9288. http://dx.doi.org/10.1039/c3nr00550j
- 38. Seo, D.H., Kumar, S. and Ostrikov, K. (2011) Control of Morphology and Electrical Properties of Self-Organized Graphenes in a Plasma. Carbon, 49, 4331-4339. http://dx.doi.org/10.1016/j.carbon.2011.06.004
- 39. Michielsen, K. and Raedt, H. (2001) Integral-Geometry Morphological Image Analysis. Physical Reports, 347, 461-538. http://dx.doi.org/10.1016/S0370-1573(00)00106-X
- 40. Lillehei, P.T., Kim, J.-W., Gibbons, L.J. and Park, C.A. (2009) Quantitative Assessment of Carbon Nanotube Dispersion in Polymer Matrices. Nanotechnology, 20, Article ID: 325708. http://dx.doi.org/10.1088/0957-4484/20/32/325708
- 41. Levchenko, I., Ostrikov, K., Mariotti, D. and Svrcek, V. (2009) Self-Organized Carbon Connections between Catalyst Particles on a Silicon Surface Exposed to Atmospheric-Pressure Ar + CH4 Microplasmas. Carbon, 47, 2379-2390. http://dx.doi.org/10.1016/j.carbon.2009.04.031
- 42. Legland, D., Kiêu, K. and Devaux, M.-F. (2007) Computation of Minkowski Measures on 2D and 3D Binary Images. Image Analysis and Stereology, 26, 83-92. http://dx.doi.org/10.5566/ias.v26.p83-92
- 43. Gouyet, J.-F. (1996) Physics and Fractal Structures. Springer-Verlag, Berlin, and Masson.
- 44. Kou, J., Liu, Y., Wu, F., Fan, J., Lu, H. and Xu, Y. (2009) Fractal Analysis of Effective Thermal Conductivity for Three-Phase (Unsaturated) Porous Media. Journal of Applied Physics, 106, Article ID: 054905. http://dx.doi.org/10.1063/1.3204479
- 45. Bacchi, O.O.S., Reichardt, K. and Villa Nova, N.A. (1996) Fractal Scaling of Particle and Pore Size Distributions and Its Relation to Soil Hydraulic Conductivity. Scientia Agricola, 53, 356-356. http://dx.doi.org/10.1590/S0103-90161996000200027
- 46. Ruffett, C., Gueguen, Y. and Darot, M. (1991) Complex Conductivity Measurements and Fractal Nature of Porosity. Geophysics, 56, 758-769. http://dx.doi.org/10.1190/1.1443093
- 47. Levchenko, I., Korobov, M., Romanov, M. and Keidar, M. (2004) Ion Current Distribution on a Substrate during Nanostructure Formation. Journal of Physics D: Applied Physics, 37, 1690-1695. http://dx.doi.org/10.1088/0022-3727/37/12/014
- 48. Douketis, C., Wang, Z., Haslett, T. and Moskovits, M. (1995) Fractal Character of Cold-Deposited Silver Films Determined by Low-Temperature Scanning Tunneling Microscopy. Physical Review B, 51, Article ID: 11022. http://dx.doi.org/10.1103/PhysRevB.51.11022
- 49. Mecke, K.R. (2000) Additivity, Convexity, and Beyond: Applications of Minkowski Functionals in Statistical Physics. Statistical Physics and Spatial Statistics, 554, 111-184. http://dx.doi.org/10.1007/3-540-45043-2_6







