Received 24 June 2015; accepted 27 July 2015; published 31 July 2015

ABSTRACT

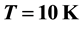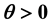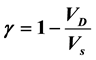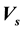Absorption of acoustic phonons was studied in degenerate Carbon Nanotube (i.e. where the electrons are found close to the Fermi level). The calculation of the hypersound absorption coefficient (G) was done in the regime where (q is the acoustic phonon number and l is the electron mean free path). At and (q being scattering angle), the dependence of G on acoustic wave number (q), frequency (), and, (and 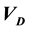being the speed of sound and the drift velocity respectively) were analysed numerically at (where n is an integer ) and presented graphically. It was observed that when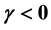, the maximum amplification was attained at 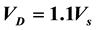which occurred at. In the second harmonics, , the absorption obtained was compared to experimental measurement of acoustoelectric current via the Weinreich relation and the results qualitatively agreed with each other.

Keywords:

Carbon Nanotube, Hyperound, Absorption, Acoustoelectric

1. Introduction

Carbon Nanotubes (CNT) are graphite sheets seamlessly wrapped into cylinders characterised by a chiral index (m, n), with m and n being two integers, which specify the carbon nanotube uniquely [1] . This has recently attracted lot of interest for use in many semiconductor devices due to its remarkable electrical, mechanical, and thermal properties which are mainly attributed to its unusual band structures [2] . The p-bonding and anti-bond- ing 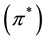energy band of CNT crosses at the Fermi level in a linear manner [3] [4] . In the linear regime, electron-phonon interactions in CNT at low temperatures lead to the emission of large number of coherent acoustic phonons. Studies of the effect of phonons on thermal transport [5] , on Raman scattering [6] and on electrical transport [7] in CNT are active areas of research. Also, the speed of electrons in the linear region is extremely high. This makes CNT a good candidate for application of high frequency electronic systems such as field effect transistors (FET’s) [8] , single electron memories [9] and chemical sensors [10] -[13] . Another important investigation in the linear regime is interaction of acoustic phonons with drift charges in CNT. It is well known that when acoustic phonons interact with charge carriers, it is accompanied by energy and momentum exchange which gives rise to the following effects: Absorption (Amplification) of acoustic phonons [14] -[17] ; Acoustoelectric Effect (AE) [18] -[21] ; Acoustomagnetoelectric Effect (AME) [22] ; Acoustothermal Effect [23] and Acoustomagnetothermal Effect [24] [25] . The idea of acoustic wave amplification in bulk material was theoretically predicted by Tolpygo and Uritskii (1956) [26] , and Weinreich [27] and in N-Ge by Pomerantz [28] . In Superlattices, the effect of hypersound absorption/amplification was extensively studied by Mensah et al. [29] - [33] , Vyazovsky et al. [34] , Bau et al. [35] , while Shmelev and Zung [36] calculated the absorption coefficient and renormalization of the short-wave sound velocity. Azizyan [37] calculated the absorption coefficient in a quantized electric field. Furthermore, Acoustic wave absorption/amplification in Graphenes [38] -[40] , Rectangular quantum wires [41] , and quantum dots [42] have all received attention. On the concept of Acoustoelectric Effect (AE) in bulk [43] [44] and low-dimensional materials, lots of researches have been comprehensively done both theoretically and experimentally. Acoustoelectric effect in CNT’s is now receiving attention with few experimental works done on it. Ebbecke et al. [45] studied the AE current transport in a single walled CNT, whilst Reulet et al. [46] studied AE in CNT. But in all these researches, there are no theoretically studies of AE in CNT. In this paper, the absorption (amplification) of hypersound in CNT in the regime 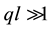(q is the acoustic wave number and l is the electron mean free path) is considered where the acoustic wave is considered as a flow of monochromatic phonons of frequency.

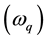It is worth noting that the mechanism of absorption (amplification) is due to Cerenkov effect. For practical use of the Cerenkov acoustic-phonon emission, the material must have high drift velocities and large densities of electrons. Carbon Nanotubes (CNT) has electron mobility of 10⁵ cm²/V∙s at room temperature. At low temperature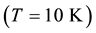, CNT exhibit good AE effect, which indicates that Cerenkov emission can take place in it [47] . The paper is organised as follows: In Section 2, the kinetic theory based on the linear approximation for the phonon distribution function is setup, where the rate of growth of the phonon distribution is deduced and the absorption coefficient (G) is obtained. In Section 3, the final equation is analysed numerically in a graphical form at various harmonics where the absorption obtained are related to the acoustoelectric current via the Wienrich relation. Lastly the conclusion is presented in Section 4.

2. Theory

We will proceed following the works of [48] [49] where the kinetic equation for the phonon distribution is given as

(1)

where represents the number of phonons with wave vector at time t. The factor accounts for the presence of phonons in the system when the additional phonon is emitted. The represents the probability that the initial state is occupied and the final electron state is empty whilst the factor is that of the boson and fermion statistics. The unperturbed electron distribution function is given by the shifted Fermi-Dirac function as

(2)

where is the Fermi-Dirac equilibrium function, with being the chemical potential, is momentum of the electron, , k is the Boltzmann constant and is the net drift velocity relative to the ion lattice site. In a more convenient form, Equation (1) can be written as

(3)

To simplify Equation (3), the following were utilised

(4)

(5)

Given that

(6)

the phonon generation rate simplifies to

(7)

In Equation (7), if. When, the system would return to its equilibrium configuration when perturbed where

But leads to the Cerenkov condition of phonon instability (amplification). The linear energy dispersion relation for the CNT is given as [50]

(8)

The is the electron energy in the Brillouin zone at momentum, b is the lattice constant, is the tight binding overlap integral. The ± sign indicates that in the vicinity of the tangent point, the bands exhibit mirror symmetry with respect to each point. The phonon and the electric field are directed along the CNT axis, therefore. Where is the scattering angle. At low temperature, the, Equation (5) reduces to

(9)

Inserting Equation (8) and Equation (9) into Equation (7), and after some cumbersome calculations yield

(10)

where, and

3. Numerical Analysis

Considering the finite electron concentration, the matrix element can be modified as

(11)

where is the electron permitivity [50] . However, for acoustic phonons, , where is the deformation potential constant and is the density of the material. From Equation (10), taking, the Equation (10) finally reduces to

(12)

where is the modified Bessel function. The parameters used in the numerical evaluation of Equation (12) are:, , , , , , and. The dependence of the absorption coefficient on the acoustic wave number, the frequency and at various harmonics are presented below. For, the graph of versus at varying frequencies and that of versus for various acoustic wave numbers are shown in Figure 1 (Figure 1(a) and Figure 1(b)). In Figure 1(a), an amplification curve was observed, where the minimum value increases by increasing but above, an absorption was obtained. In Figure 1(b), it was observed that absorption switched over to amplification when the values were increased.

For (first harmonics), in Figure 2(a), it was observed that absorption exceed amplification and the peaks shift to the right. A further increase in values caused an inversion of the graph where amplification exceeds absorption (see Figure 2(b)). A similar observation was seen in Figure 3 (Figure 3(a) and Figure 3(b)), where the peak values shifted to the right and decreased with increasing values (see Figure 3(a)) but in Figure 3(b), an inversion of the graph occurred for increasing values of.

Figure 4 (Figure 4(a) and Figure 4(b)) shows the dependence of on by varying either or. In both graphs, when, produce non-linear graphs which satisfy the Cerenkov condition, but at, the graph returns to zero. The observed peaks in Figure 4(a) shift to the left by increasing whilst in Figure 4(b), shift to the right by increasing.

For further elucidation, a 3D graph of versus and or versus and are presented in Figure 5 (Figure 5 (a) and Figure 5 (b)). In both graphs, when, a maximum amplification was obtained.

For (Second harmonics), the dependence of the absorption coefficient on is presented in 2D and 3D form as shown in Figure 6 and Figure 7. In Figure 6, an absorption graph was obtained. The insert shown is an experimental results obtained for the Acoustoelectric current in Single walled Carbon Nanotube. Figure 7 (Figure 7(a) and Figure 7 (b)) is the 3D representation of the absorption in second harmonics.

From Weinreich relation [33] , the absorption coefficient is directly related to the acoustoelectric current, therefore from Figure 6, the results obtained for the absorption coefficient qualitatively agrees with the experimental results presented (see insert). In the 3D graphs, the maximum amplification and absorption occurs at

which is equivalent to, with the electric field gives.

4. Conclusion

The expression for Hypersound Absorption of acoustic phonons in a degenerate Carbon Nanotube (CNT) was deduced theoretically and graphically as presented. In this work, the acoustic waves were considered to be a flow of monochromatic phonons in the short wave region. The general expression obtained was analysed numerically for (where n is an integer). From the graphs, at certain values of and, an Amplification was observed to exceed Absorption or vice-versa. For, the maximum Amplification was observed at which gave us a field of. This field was far lower than that observed in superlattice and homogeneous semiconductors permitting the CNT to be a suitable material for hypersound generator (SASER). A similar expression can be seen in the works of Nunes and Fonseca.

What is very interesting to our work is the qualitative agreement of the absorption graph to an experimental graph resulting from an acoustoelectric current via the Weinriech relation.

Cite this paper

K. A.Dompreh,N. G.Mensah,S. Y.Mensah,S. S.Abukari,F.Sam,R.Edziah, (2015) Hypersound Absorption of Acoustic Phonons in a Degenerate Carbon Nanotube. Graphene,04,62-74. doi: 10.4236/graphene.2015.43007

References