Graphene
Vol.03 No.04(2014), Article ID:50635,10 pages
10.4236/graphene.2014.34009

Transmission of Terahertz Acoustic Waves through Graphene-Semiconductor Layered Structures

Shuhui Zhang1, Wen Xu1,2*, Francois M. Peeters3

1Key Laboratory of Materials Physics, Institute of Solid State Physics, Chinese Academy of Sciences, Hefei, China

2Department of Physics, Yunnan University, Kunming, China

3Department of Physics, University of Antwerp, Antwerpen, Belgium

Email: *wenxu_issp@aliyun.com

Copyright © 2014 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 24 August 2014; revised 18 September 2014; accepted 17 October 2014

ABSTRACT

We present a theoretical study of the acoustic properties of graphene-semiconductor layered structures. The transmission coefficient for longitudinal acoustic waves through the structure is evaluated by using the usual transfer matrix method. We find that the finite thickness of the graphene layer can affect significantly the transmission spectrum of the proposed structure. The features of the sound transmittance depend strongly on the number of the graphene layers. For multi-layer graphene-semiconductor structures, the sound transmission spectrum looks very similar to that for an ideal superlattice. For such structures, terahertz acoustic forbidden gap can be observed even when a thick semiconductor layer is considered. These results are the consequence of the Bragg’s condition for sound waves. This study is relevant to the exploration of the acoustic properties of graphene-based layered structures and to the application of graphene as high-fre- quency acoustic devices.

Keywords:

Graphene, Layeres Structure, Sound Transmittance, Finite Thickness

1. Introduction

It is known that graphene is a single layer of carbon atoms covalently bonded together in a honeycomb structure. The electron dynamics in graphene obeys two-dimensional (2D) massless Dirac equation with a linear energy dispersion [1] . Because graphene is a gapless semiconductor system as well as an ideal 2D electron gas system, intensive theoretical and experimental investigations have been carried out worldwide in recent years in exploring the unique and important physical properties of graphene-based systems [2] . Graphene has shown a wealth of excellent performance in all respects of mechanics, electronics, optics and optoelectronics, such as high Young’s modulus [3] , high carrier mobility at room temperature [4] , high light transmittance [5] , to men- tion but a few. In fact, graphene has already been utilized to realize high-speed and high-frequency electronic devices such as field-effect transistors [6] , single-electron transistor [7] , flexible touch screen [8] , transparent electrodes for visible [9] and infrared [10] optoelectronic devices, etc.

In particular, alternative route to harnessing the properties of graphene for practical device applications would be to incorporate graphene sheets in a complex material structure [11] . It is known that in a complex material system, the modulation of physical properties in different material layers can result in new natures of the physical properties in the combined system. For example, the layered structures consisting of different materials have been widely applied in realizing semiconductor heterostructures such as quantum wells and superlattices (SLs) to form low-dimensional electronic systems. Especially, the investigation into acoustic properties of layered complex materials has been intensive and fruitful so far. An in-depth understanding of the phonon behavior in these advanced material systems has been greatly achieved [12] . One of the most fundamental acoustic properties of a SL is the Bragg reflection of long wavelength phonons or sound waves. We know that for normal incidence, the Bragg reflection condition for sound waves in a SL reduces simply to:

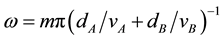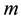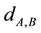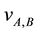, where is an integer; and are respectively the width and sound

velocity in different SL layers 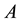and 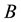[13] . Thus, we are able to tune and modulate the propagation of high-frequency acoustic waves by engineering the SL structures. In fact, SL-based high-frequency acoustic devices such as filters, mirrors, and resonators for sound waves have been realized experimentally [14] . In these acoustic devices, normally the short-period SL structures are required in order to achieve a strong modulation of the acoustic properties by the presence of the hetero-material systems.

In recent years, a big progress has been made to achieve the electric and optic generation of coherent acoustic waves in terahertz (1012 Hz or THz) frequency range from different semiconductor systems [15] . In this work [15] , through the application of an electrical bias to a weakly coupled semiconductor superlattice, they observed experimentally the amplitude increase of the coherent hypersound oscillations generated by a femtosecond optical pulse and the spectral narrowing of the SL phonon mode with a frequency 441 GHz. These results show that coherent amplification of phonons due to stimulated emission in the SL under electrical pumping and provides an essential step towards coherent generation of THz sound and other active hypersound devices. This offers us a chance to investigate hypersonic properties of condensed matter materials and to explore the applications of ultrahigh-frequency acoustic waves. Therefore, the study of THz sound waves and related hypersonic devices has become an important and significant field of research in terms of fundamental research and of device applications. We know that graphene is an ideal 2D crystal formed by single or few layer of carbon atoms. Thus, graphene can provide us with an ideal material which is ultrathin in one spacial direction but with large in-plane area size [16] . When combining graphene with conventional semiconductor material to form a layered complex structure, the significant difference of physical properties in graphene and in semicond uctor layer allows us to expect some novel and unique physical properties in the complex structure. Particularly, we know that the density and sound velocity in graphene differ significantly from those in conventional semiconductors. One therefore can predict that the graphene-semiconductor layered structure can show some interesting features for high-frequency sound wave modulation and propagation. Because the thickness of the graphene layer is in nanometer scale, graphene-based layered structure can be utilized to design and fabricate hypersonic devices in the THz regime. Moreover, such structure gives us a freedom to engineer the graphene- based phononic crystal with, e.g., an acoustic band-gap and to study high-frequency elastic properties of the constituent material systems [17] . The prime motivation of the present study is to examine theoretically the acoustic properties of graphene-based layered structure. The paper is organized as follows. In Section 2, we develop a theoretical approach to calculate the acoustic transmission rate in graphene-semiconductor layered structures. The numerical results obtained from this study are presented and discussed in Section 3 and the main conclusions drown from this study are summarized in Section 4.

2. Theoretical Approach

In this work, we propose a layered structure which consists of a periodic sequence of alternate stacking of semiconductor and graphene constituent layers. Such a graphene-based layered structure is a kind of finite period superlattice (SL). A schematic diagram of this system is shown in Figure 1 which is similar to the Figure 1(b) in Ref. [18] . The thickness of semiconductor (A) layer and graphene (G) layer are denoted by 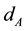and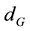. 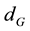is dependent on the layer number of graphene sheet which is regarded as embedded layer. We note that the interaction between semiconductor and graphene layers is usually the Van de Waals force [19] which is not the covalent band at the interface in the usual system [20] . Thus, the crystal properties are not affected significantly near the interfaces of the graphene-semiconductor layered structures. As a result, the standard continuum model based on a macroscopic picture [21] still holds for graphene-semiconductor layered structures. We consider a case where the direction of the propagation of acoustic waves is parallel to the growth direction of the structure (taken along the 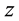direction). In this case, different phonon modes are decoupled from each other if the interfaces are considered to be the mirror-symmetry plane [18] . For simplicity, we only consider the longitudinal modes in this case. Using the continuum model for the lattice vibration, the one-dimensional wave equation can be written as

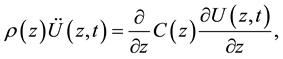(1)

where is the mass density and 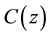is the elastic stiffness constant in different material layers. Furthermore, the solution to the wave equation in each layer can expressed in terms of a linear combination of the transmission and reflection waves:

(2)

with

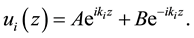(3)

Here, is an index specifying the constituent material, is the angular frequency of the acoustic wave, and is the wave number and the sound velocity in each constituent layer. In this study, we employ the transfer matrix method to calculate the acoustic coefficients of graphene-semiconductor layered systems. In doing so, it is convenient to introduce a two-component vector

(4)

Figure 1. Schematic diagram of graphene-semiconductor layered structure. The acoustic waves travel from the substrate layer and are measured in the detection layer. The layered structure is with alternate stacking of semiconductor layer and graphene layer. The growth direction is along the axis and the stacking order is denoted as. The thicknesses of the semiconductor and graphene layers are and, respectively, and the periodicity of the structure is. The period number of the structure is.

with being the layer order. We consider that the incident acoustic waves are launched at the substrate surface (see Figure 1). Thus, both the incident and reflection acoustic waves exist in the substrate layer but only the transmission waves can reach to the detection layer [22] , as shown in Figure 1. Here we are interested in a case where for simplicity [23] . By considering the continuity of the lattice displacement and the stress at the interfaces, we have

(5)

with being the number of period of the structure (see Figure 1). The transfer matrix for the whole system can be written as with

(6)

(7)

and

(8)

Here, with being the thickness of the constituent layer and with being the acoustic impedance of the constituent material. Therefore, for a finite period number, we have to calculate the transfer matrix. From the time reversal invariance of the wave equation [24] , the matrix for a single cell can be written as

(9)

with, , , , , and

. We note that because of the conservation of the probability [24] . There are several practical ways to calculate the power of a unimodular 2 × 2 matrix [24] . One way to diagonalize the matrix is presented in Appendix. Thus, we obtain

(10)

where, , , , ,

, , , and. Due to time reversal invariance of the

wave equation and the conservation of the probability, the matrix has a form similar to the matrix. Thus, we can study even more complicated layered structures such as multi-superlattice structures [25] ). The transmission rate or transmittance of the acoustic wave is defined [18] as (transmitted flux)/(incidence flux), which takes a simple form

(11)

Using Equation (11), the transmission coefficient of the longitudinal acoustic wave can be obtained for graphene-based layered structure with a given number of period. If the layered structure is with infinite number of period, it becomes the ideal superlattice structure. In such a case, the condition of the Bloch periodicity must be satisfied,

(12)

Combining Equation (5) and Equation (12), we have

(13)

where is a unit 2 × 2 matrix. After solving Equation (13), we obtain the dispersion relation for the ideal graphene-semiconductor SL as

(14)

Using Equation (11) and Equation (14), the acoustic transmission coefficient for graphene-semiconductor SL structure can be evaluated.

3. Numerical Results and Discussions

As an example, here we take silicon as semiconductor layer for the graphene-based layered structure, i.e., A = Si. The sample parameters are taken as follows: the thickness of silicon layer is 110 Å (~20 mono-layers), the bulk density and the elastic stiffness constant (ESC) for Si [26] are and , respectively. The areal density [27] and monolayer thickness [3] for graphene sheet are and dG = 3.35Å respectively. Furthermore, for graphene, we take the bulk density as and is taken as the ESC value for graphite along the c-axis [28] .

In the proposed system, the existence of the graphene layers can lead to the discontinuity of the elastic properties in different material layers. Thus, the graphene layer can affect the propagation of the acoustic waves. First of all, it is necessary to examine the appropriate treatment of the graphene layer. Due to the ultrathin nature of the monolayer graphene (MLG), one may regard it as a -like layer (i.e., roughly the null thickness). In Figure 2, we show the transmission spectra of the longitudinal sound waves through a graphene-Si layered structure with two considerations of the graphene thickness. One considers the finite thickness of the MLG sheet, and another takes the MLG as a -like layer. When taking the MLG as a -like layer, the results can be obtained by taking the limit of the finite model [24] , i.e., taking but a finite areal density in Equation (11). Figure 2 demonstrates that the transmission spectra of layered structure obtained by taking the MLG as a -like layer (delta model) and by considering the finite thickness of the MLG (finite model). As can be seen, two models lead to significantly different results. Especially, the variation of the

Figure 2. The transmission spectrum of the longitudinal acoustic wave through a graphene-based layered structure. The results obtained from taking graphene as a -like layer (delta model, solid curve) and considering a finite thickness for graphene sheet (finite model, dashed curve) are shown and compared. The results are obtained for the number of period and the acoustic frequency is.

transmission amplitude for delta model is much lower than that for finite model. This indicates that although it is very thin, the thickness of the MLG sheet affects effectively the propagation of the acoustic waves. As a result, the finite thickness of the MLG should be considered for calculating rightly the acoustic coefficients of the layered structures. The reason why the delta model cannot describe rightly the transmission of the acoustic wave is similar to the case of the transmission of electrons through a -like potential well [24] . For the transmission of electrons through a very narrow but not deep enough potential well, the finite thickness of the potential well should be considered [24] . For case of graphene-Si layered structure, is not much bigger than. Thus, the discontinuity of elastic properties in different material layers is not large enough. Hence, the thickness of the graphene layer can affect markedly the acoustic transmission of the structure. In particular, the thickness of multi-layer graphene sheet should be more seriously considered for numerical calculations.

Because the thickness of embedded graphene layer is crucial to acoustic transmission through the structure, we should examine the influence of the layer number of embedded graphene sheet on the transmission spectrum. In Figure 3, the acoustic transmission spectra are shown at a fixed period number for mono-, bi-, and five-layer graphene sheet. The transmission spectra show obvious peaks and valleys, resulting from the interference effect due to the reflection of the acoustic waves. The valley frequencies in the transmission spectrum correspond to the constructive interference of the reflection, determined by the Bragg’s condition [18] :

, with denoting the order of the Bragg’s condition. Under

the Bragg’s condition for interference of the reflection, the peak frequencies in the transmission spectrum are

induced by destructive interference, determined by. Considering that the

transmission spectrum is an overall consequences of the propagation and reflection of the acoustic waves with different frequencies, we note that the peak and valley frequencies are not exactly corresponding to the interference conditions. It should be pointed out that the difference in the acoustic transmission spectra for different graphene layers can be utilized to characterize the material features of the grahene sheet. As we know, at present the graphene based systems have been characterized mainly by optical and electronic measurements such as Raman spectrum, optical spectroscopy, electron microscopy, etc. [16] . Because the obvious peak and valley patten can be observed, the acoustic transmission of layered structure with graphene as embedded layer can be applied to identify the graphene sheet with different numbers of the carbon layer.

The results shown in Figure 3 are for layered structures with small period number. It is helpful to look into the evolution of acoustic transmission through the structure with increasing period number. In the left panel of Figure 4, we show the dispersion relation of the acoustic waves in an infinite period Si/MLG SL. The stop bands for the acoustic wave vectors appear in the folded Brillouin zone and at its boundaries. This indicates

Figure 3. The acoustic transmission spectra in graphene-based layered structures for three different layer numbers of embedded graphene. The solid, dashed, dotted curves corre- spond, respectively, to mono-, bi- and five-layer graphene sheet. The period number is and the acoustic fre- quency is.

Figure 4. (Left panel) Dispersion relation of the acoustic waves for an infinite period of Si/MLG SL. Stop bands appear in the folded Brillouin zone and at its boundaries. (Middle panel) Acoustic transmission spectrum at normal incidence in a Si/MLG layered structure with a period. (Right panel) Transmission spectrum in a Si/MLG layered structure with.

that the Si/MLG SL can modulate effectively the propagation of the acoustic waves. In the middle and right panels of Figure 4, the acoustic transmission spectra are shown for Si/MLG structures with finite periods and respectively. The prominent dips in transmission spectrum correspond exactly to the frequency gaps in the dispersion relation shown in the left panel of Figure 4. Thus, we can look into the correlation between the width of the forbidden bands and the magnitude of the transmission dips for a SL structure and a structure with finite period. Although the decrease in the number of period does not alter the frequency range of the transmission dips, there are shallower dips and more visible oscillations in the transmission spectrum for the structures with finite period number. The magnitude of the dips reflects the discrepancy of the actual finite number of periods from ideal SL with infinite periods. The small oscillations in the transmission spectrum is caused by the interference effects and the corresponding frequency increases with decreasing number of period. Hence, the small oscillations can be more easily observed in the transmission spectrum for a device structure with smaller period number. Such interesting features have been observed in conventional SL systems, e.g., in GaAs/AlAs SLs [18] . However, due to the ultrathin nature of the graphene sheet, the transmission patten for acoustic waves can be observed in the THz regime. This finding suggests that the graphene-semiconductor layered structures can be applied to achieve high-frequency manipulation of the acoustic waves according to the Bragg’s condition. In Figure 4, although we have chosen a relatively thick semiconductor layer, the forbidden gaps for acoustic wave transmission still appear in the THz bandwidth. Thus, the graphene-semiconductor layered structures can be taken as a basic component for designing and fabricating of THz acoustic devices applied in the areas such as nano-phononics [29] .

It should be noted that although the mechanical properties of graphene have been widely studied theoretically and experimentally [30] , there has been no direct report so far for the value of the ESC for graphene. In Figures 2-4, we choose C33 to be that in graphite for numerical calculations. So it is necessary to examine the influence of the ESC value on the acoustic transmission in the layered structure. In Figure 5, the acoustic trans mission spectrum is shown for bi-layer graphene embedded in the structure with period number for different ESC values. We can see a slight peak shift and relatively big amplitude variation in the transmission spectrum with varying the value of the ESC. The peak shift in the transmission spectrum can be understood on the basis of the interference condition. The slight blue-shift of the peaks is induced by slightly larger sound velocity with increasing ESC value. Thus, although the value of the ESC for graphene can affect the transmission intensity relatively strongly, the basic patten of the transmission spectrum for the structure does not change significantly with the ESC.

Figure 5. The acoustic transmission spectrum in graphene- based layered structure for different elastic stiffness constants (in the unit of GPa). The bi-layer graphene is embedded in the structure and the number of period is.

4. Conclusions

In this work, we have studied theoretically the acoustic properties of graphene-semiconductor layered structures. The acoustic transmission coefficient has been evaluated by using the standard transfer matrix method. The main conclusions obtained from this study are summarized as follows.

1) We have shown that although graphene is a very thin material, the finite thickness of the graphene sheet should be considered in order to calculate rightly the transmission spectrum of the graphene-based layered structure. 2) We have found that the acoustic transmission spectrum depends drastically on the layer numbers of the graphene sheet which is embedded between the semiconductor layers. Because the obvious peak and valley patten induced by the interference effect of the acoustic waves can be observed and measured, the transmission spectrum of the layered structure with graphene as embedded layer can be applied to characterize graphene sheet with different layer numbers. 3) The essential feature of such layered structures is the presence of the forbidden transmission gaps in the THz bandwidth. This is induced by the difference of the mechanical properties in different material layers and by the periodic structure of the proposed system [30] . With increasing the period numbers of the layered structure, the acoustic transmission approaches to the case of an ideal superlattice. More importantly, due to the ultrathin nature of the graphene layer, the forbidden gaps of the acoustic transmission in the graphene-based layered structure are in the THz bandwidth. Thus, the graphene-semiconductor layered structures can be applied as a basic component to design and fabricate THz acoustic devices such as phonon filter [29] and phonon mirror [31] . We hope these interesting and important findings can help us to gain an in-depth understanding of the acoustic properties of graphene-based compound structures.

Acknowledgements

This work was supported by the Ministry of Science and Technology of China (Grant No. 2011YQ130018), Department of Science and Technology of Yunnan Province, and by the Chinese Academy of Sciences.

References

  1. Neto, A.H.C., Guinea, F., Peres, N.M.R., Novoselov, K.S. and Geim, A.K. (2009) The Electronic Properties of Grapheme. Reviews of Modern Physics, 81, 109-162. http://dx.doi.org/10.1103/RevModPhys.81.109
  2. Das Sarma, S., Geim, A.K., Kim, P. and MacDonald, A.H. (2007) Exploring Graphene―Recent Research Advances― Foreword. Solid State Communications, 143, 1-2. http://dx.doi.org/10.1016/j.ssc.2007.04.030
  3. Lee, C., Wei, X.D., Kysar, J.W. and Hone, J. (2008) Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science, 321, 385-388. http://dx.doi.org/10.1126/science.1157996
  4. Morozov, S.V., Novoselov, K.S., Katsnelson, M.I., Schedin, F., Elias, D.C., Jaszczak, J.A. and Geim, A.K. (2008) Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Physical Review Letters, 100, Article ID: 016602. http://dx.doi.org/10.1103/PhysRevLett.100.016602
  5. Kuzmenko, A.B., van Heumen, E., Carbone, F. and van der Marel, D. (2008) Universal Optical Conductance of Graphite. Physical Review Letters, 100, 117401-117404. http://dx.doi.org/10.1103/PhysRevLett.100.117401
  6. Lin, Y.M., Dimitrakopoulos, C., Jenkins, K.A., Farmer, D.B., Chiu, H.Y., Grill, A. and Avouris, P. (2010) 100-GHz Transistors from Wafer-Scale Epitaxial Graphene. Science, 327, 662-662. http://dx.doi.org/10.1126/science.1184289
  7. Stampfer, C., Schurtenberger, E., Molitor, F., Güttinger, J., Ihn, T. and Ensslin, K. (2008) Tunable Graphene Single Electron Transistor. Nano Letters, 8, 2378-2383. http://dx.doi.org/10.1021/nl801225h
  8. Bae, S., Kim, H., Lee, Y., Xu, X., Park, J.S. and Zheng, Y. (2010) Roll-to-Roll Production of 30-Inch Graphene Films for Transparent Electrodes. Nature Nanotechnology, 5, 574-578. http://dx.doi.org/10.1038/nnano.2010.132
  9. Hogan, H. (2008) Fabricating Photonic Quantum Circuits in Silicon. Photonics Spectra, 42, 17-19.
  10. Xu, W., Gong, Y.P., Liu, L.W., Qin, H. and Shi, Y.L. (2011) Can Graphene Make Better HgCdTe Infrared Detectors? Nanoscale Research Letter, 6, 250. http://dx.doi.org/10.1186/1556-276X-6-250
  11. Stankovich, S., Dikin, D.A., Dommett, G.H.B., Kohlhaas, K.M., Zimney, E.J., Stach, E.A., Piner, R.D., Nguyen, S.T. and Ruoff, R.S. (2006) Graphene-Based Composite Materials. Nature, 442, 282-286. http://dx.doi.org/10.1038/nature04969
  12. Jusserand, B. and Cardona, M. (1989) Light Scattering in Solids V. Springer, Heidelberg, 49.
  13. Sapriel, J. and Djafari-Rouhani, B. (1989) Vibrations in Superlattices. Surface Science Reports, 10, 189-275. http://dx.doi.org/10.1016/0167-5729(89)90003-4
  14. Narayanamurti, V. (1981) Phonon Optics and Phonon Propagation in Semiconductors. Science, 213, 717-723. http://dx.doi.org/10.1126/science.213.4509.717
  15. Beardsley, R.P., Akimov, A.V., Henini, M. and Kent, A.J. (2010) Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice. Physical Review Letter, 104, Article ID: 085501. http://dx.doi.org/10.1103/PhysRevLett.104.085501
  16. Cooper, D.R., D’Anjou, B., Ghattamaneni, N., Harack, B., Hilke, M., Horth, A., Majlis, N., Massicotte, M., Vandsburger, L., Whiteway, E. and Yu, V. (2012) Experimental Review of Graphene. ISRN Condensed Matter Physics, 2012, Article ID: 501686. http://dx.doi.org/10.5402/2012/501686
  17. El Boudouti, E.H., Djafari-Rouhani, B., Akjouj, A. and Dobrzyski, L. (2009) Acoustic Waves in Solid and Fluid Layered Materials. Surface Science Reports, 64, 471-594. http://dx.doi.org/10.1016/j.surfrep.2009.07.005
  18. Tamura, S., Hurley, D.C. and Wolfe, J.P. (1988) Acoustic-Phonon Propagation in Superlattices. Physical Review B, 38, 1427-1449. http://dx.doi.org/10.1103/PhysRevB.38.1427
  19. Wang, Y.Y., Ni, Z.H., Yu, T., Shen, Z.X., Wang, H.M., Wu, Y.H., Chen, W. and Wee, A.T.S. (2008) Raman Studies of Monolayer Graphene: The Substrate Effect. Journal of Physical Chemistry C, 112, 10637-10640. http://dx.doi.org/10.1021/jp8008404
  20. Yu, P.Y. and Cardona, M. (2001) Fundamentals of Semiconductors: Physics and Materials Properties. 3rd Edition, Springer, Berlin.
  21. Landau, L.D. and Lifschitz, E.M. (1986) Theory of Elasticity. Pergamon, Oxford.
  22. Mizuno, S. and Tamura, S.I. (1992) Theory of Acoustic-Phonon Transmission in Finite-Size Superlattice System. Physical Review B, 45, 734-741. http://dx.doi.org/10.1103/PhysRevB.45.734
  23. Mizuno, S. (2005) Acoustic Phonons in Nanowire Superlattices: Azimuthally Symmetric Torsional Modes. Physical Review B, 71, Article ID: 085303. http://dx.doi.org/10.1103/PhysRevB.71.085303
  24. Griffiths, D.J. and Steinke, C.A. (2001) Waves in Locally Periodic Media. American Journal Physics, 69, 137-154. http://dx.doi.org/10.1119/1.1308266
  25. Tamura, S.I. (1991) Resonant Transmission of Acoustic Phonons in Multisuperlattice Structures. Physical Review B, 43, Article ID: 12646. http://dx.doi.org/10.1103/PhysRevB.43.12646
  26. Madelung, O. (1991) Semiconductors: Group IV and III-V Compounds. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-45681-7
  27. See, E.G., Xu, W., Dong, H.M., Li, L.L., Yao, J.Q., Vasilopoulos, P. and Peeters, F.M. (2010) Optoelectronic Properties of Graphene in the Presence of Optical Phonon Scattering. Physical Review B, 82, Article ID: 125304. http://dx.doi.org/10.1103/PhysRevB.82.125304
  28. Mohr, M., Maultzsch, J., Dobardzic, E., Reich, S., Milosevic, I., Damnjanovic, M., Bosak, A., Krisch, M. and Thomsen, C. (2007) Phonon Dispersion of Graphite by Inelastic X-Ray Scattering. Physical Review B, 76, Article ID: 035439. http://dx.doi.org/10.1103/PhysRevB.76.035439
  29. Lanzillotti-Kimura, N.D., Fainstein, A., Lemaître, A. and Jusserand, B. (2006) Nanowave Devices for Terahertz Acoustic Phonons. Applied Physics Letters, 88, Article ID: 083113. http://dx.doi.org/10.1063/1.2178415
  30. See, E.G., Cadelano, E., Palla, P.L., Giordano, S. and Colombo, L. (2009) Nonlinear Elasticity of Monolayer Graphene. Physical Review Letters, 102, Article ID: 235502. http://dx.doi.org/10.1103/PhysRevLett.102.235502
  31. Lanzillotti-Kimura, N.D., Fainstein, A., Huynh, A., Perrin, B., Jusserand, B., Miard, A. and Lemaître, A. (2007) Coherent Generation of Acoustic Phonons in an Optical Microcavity. Physical Review Letters, 99, Article ID: 217405. http://dx.doi.org/10.1103/PhysRevLett.99.217405

Appendix

In this Appendix, we present a brief derivation for getting the power of a particular kind of 2 × 2 matrix. Usually, it is difficult to get a simple analytical form for the power of a matrix. However, the case is different when a matrix takes a form

(A1)

We consider an eigenvalue problem corresponding to the matrix, i.e.,. The eigenvalue and the eigenvector can be written as:, , , and. Here, , , , and. Moreover,

(A2)

In order to calculate the power of, we introduce the transformation matrix

(A3)

and its inverse

(A4)

It is easily to verify. Thus, the power of matrix can be written as

(A5)

where

(A6)

For straight calculation, we get

(A7)

Finally, the power of becomes

(A7)

Here, we have defined and. We note that and are both real whatever is real or imaginary.

NOTES

*Corresponding author.

Journal Menu >>