ABSTRACT

Recently, several institutions have been developing magnetic resonance imaging (MRI)-guided radiotherapy treatment systems. In this study, we examine whether it is possible to perform radiation therapy planning (RTP) using a magnetic susceptibility map obtained using MRI. The head of a healthy volunteer was scanned using dual-energy computed tomography (CT) and MRI. A T2-star-weighted 3D gradient echo-based sequence (GRE) with images taken at four different echo times was acquired using the MRI scanner. The CT images were converted to relative electron density (rED) using a predefined ΔCT-rED conversion table. ΔCT was derived using the energy-sub- traction method. The rED map was obtained from a single-linear relationship with the ΔCT-rED conversion table, whereas the magnetic susceptibility map was obtained from quantitative susceptibility mapping (QSM) via MRI. Subsequently, to obtain the relationship between the magnetic susceptibility and the rED, the rED map was rigidly aligned to the susceptibility map and resampled at the susceptibility map’s resolution. Finally, the magnetic susceptibility rED conversion table was obtained via voxel-by-voxel mapping between the two maps. No strong relationship between magnetic susceptibility and rED was obtained in the healthy volunteer’s head or in this study. The coefficient correlation between these parameters was 0.0145. Magnetic susceptibility values may be not able to convert to rED using our proposed method in healthy volunteer’s head. In contrast to the magnetic-susceptibility values obtained from the QSM algorithm, which were strongly affected by calcification and iron content, the rED or CT number was not considerably affected by such materials.

Keywords:

Magnetic Susceptibility, Quantitative Susceptibility Mapping, MRI-Based Radiation Therapy Planning

1. Introduction

To date, medical facilities have mostly used X-ray-based imaging modalities, such as the On-Board Imaging system, cone-beam computed tomography, Electronic Portal Imaging Device, orthogonal X-ray imaging system (Exac Track, BrainLAB AG, Germany), and Megavoltage computed tomography (Tomotherapy, Accuray Inc, Sunnyvale, CA, USA), as imaging modalities for image- guided radiation therapy (IGRT), which aim to decrease geometric uncertainties during radiotherapy using image guidance [1] [2] [3] [4] . These X-ray-based imaging modalities can easily visualize high-density materials, such as bone and fiducial markers; however, the visualization of low-density materials, such as soft tissues and tumors, is limited. Hence, when we use X-ray-based imaging modalities for IGRT, we often match bone or fiducial markers between planned and obtained images just before the treatment and indirectly obtain tumor positions from matching high-density materials.

Recently, several institutions have been developing magnetic resonance imaging (MRI)-guided radiotherapy treatment systems (i.e., MRgRT or MRIgRT) [5] [6] . The principle behind such systems is using the MRI machine as an imaging modality for IGRT. MR images have an excellent soft-tissue contrast and facilitate a soft-tissue- or tumor-based patient setup with no additional exposure. Furthermore, MRgRT has the potential to reduce the setup margin and adaptive radiation therapy. In order to incorporate MRI images into radiotherapy, several problems and methods for addressing them have been reported by numerous researchers [5] [6] . MRI images have problems with regard to image-distortion, resulting from magnetic-field inhomogeneity induced by a tissue’s magnetic susceptibility, and the effect of image distortion has been discussed in previous studies [1] [2] [3] [4] [7] [8] [9] . Furthermore, these previous studies have proposed various correction methods to mitigate such undesirable effects. MRI provides superior image quality for soft tissue delineation compared to computed tomography (CT) and is widely used for target and organ delineation in radiotherapy treatment planning (RTP) [10] [11] [12] . The intensity of CT images is directly related to electron density. Therefore, CT is used for attenuation correction of the doses calculated in RTP. The major challenge in the application of MRI to RTP is the fact that there exists no physical relationship between MR-signal intensities and electron densities. The feasibility of MR-based dose calculation has been demonstrated for radiotherapy on different treatment regions using manual segmentation and bulk-density assignment [13] [14] . Conversion from MRI to pseudo-CT images has also been reported using anatomy- and voxel-based methods. Anatomy-based methods use deformable image registration between MRI and CT images to obtain deformed MRI or CT images. The drawback of this method is the uncertainty of the registration [15] . Voxel-based methods can avoid dependence on image registration by direct conversion of MRI signal-intensity values to Hounsfield units (HU) or electron densities [16] [17] . Previous studies on voxel-based methods have used ultrashort echo time sequences to segment tissue into soft tissue, bone, and air.

The abovementioned correction methods and MRI sequences are used for MRI-based RTP. On the other hand, a new quantitative value, magnetic susceptibility, has been utilized in clinical research in addition to the T₁, T₂, and ADC values [18] [19] [20] [21] . Magnetic susceptibility is a physical property of a material that may assist with the detection and quantification of specific biomarkers such as gadolinium, calcium, and iron to assess brain physiology and pathology. A magnetic susceptibility map was generated by deconvolution between the local magnetic field and the dipole kernel. This field was obtained from phase data from gradient echo sequences including not only true signals but also noises and artifacts from hardware and human bodies. The dipole kernel was obtained by approximation, and if deconvolution was performed in the Fourier domain, the coefficients of the dipole kernel become zero on the surface of the cone in k-space [22] . Hence, deconvolution between the local magnetic field and the dipole kernel was ill-condition. Recently, however, several approaches have been reported for solving this challenging inverse problem to obtain magnetic susceptibility maps [23] [24] [25] [26] [27] .

This study describes our investigation of the feasibility of a voxel-based method for directly converting magnetic susceptibility (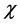) into relative electron density (rED). Chen et al. showed that the total CT number and total susceptibility are strongly correlated in calcification regions [28] . We examined over the entire brain whether there is a correlation between these quantities. Because χ values are quantitative and if rED can be obtained from χ, MR images can be used instead of CT images in radiotherapy planning.

2. Materials and Methods

2.1. Morphology Enabled Dipole Inversion for Quantitative Susceptibility Mapping

To obtain the magnetic susceptibility map, we used the morphology enabled dipole inversion (MEDI) approach [24] . MEDI utilizes a constrained L₁ norm- minimization problem,

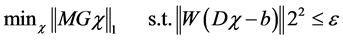. (1)

where M is the weighting matrix derived from the gradient of the magnitude image. G denotes the gradient operator, W is a weighting matrix proportional to the image magnitude to compensate for the noise variation in the field measurements, and is the noise level. MEDI minimizes the number of voxels that belong to the edges in the magnetic susceptibility map but not the edges in the magnitude image. Therefore, we need to estimate the local magnetic field for QSM using the following formula

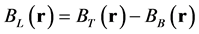. (2)

where B_L(r) is the local magnetic field, B_T(r) is the total magnetic field, and B_B(r) is the background field induced by outside of W. B_T(r) is proportional to the measured signal phase 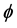and is given as follows:

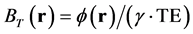. (3)

where is the gyromagnetic ratio of the ¹H nucleus and TE is the time to echo in a gradient echo sequence. To avoid aliasing of the frequency distribution and obtain a robust three-dimensional phase map, we performed phase unwrapping [2] . Then, B_B(r) could be approximated using projection onto dipole field (PDF) algorithm [29] , which allows us to obtain B_L(r). The data processing chain for QSM is schematically illustrated in Figure 1.

2.2. Generation of a Single-Linear Relationship for the Dual-Energy Subtraction ΔHU − rED Conversion Table

The conversion of the computed-tomography number (HU) into an electron density relative to water is used in treatment planning for radiation therapy. The 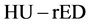conversion is performed using tissue substitutes with known electron densities in calibration phantoms [30] . However, because the CT numbers obtained from tissue-attenuation coefficients depend upon both electron densities and effective atomic numbers, the 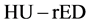conversion table did not express a one-to-one relationship. Hence, we used 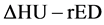conversion method, for which ΔHU was the energy subtracted HU derived from dual energy computed tomography [31] [32] [33] . This 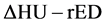conversion method can finally generate a single relationship between HU (ΔHU) and rED. ΔHU is defined as follows:

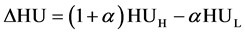. (4)

where is the weighting factor for the subtraction, with H and L representing the CT values from the high and low energy kV scans, respectively. Thus, we can obtain the single relationship between ΔHU and rED given by the following equation:

. (5)

where a and b are constant.

To obtain a single relationship between ΔHU and rED, we scanned a tissue-characterization phantom GAMMEX 467 (Gammex Inc., Middleton, WI) with 14 inserts made of different materials using a CT scanner (LightSpeed RT 16, GE Healthcare, Milwaukee, WI). This scanner could not perform a dual- energy scan, so instead we performed two single-energy scans at different energies. The CT scans were performed with the following parameters: tube voltage = 80 and 120 kVp; tube current = 350 mA; FOV = 300 × 300 mm²; matrix size = 512 × 512; slice thickness = 2.5 mm. Figure 2(a) and Figure 2(b) show scanned high-kV and low-kV CT images, respectively. This algorithm was implemented in Mathematica (Wolfram Research, Inc., Champaign, IL).

2.3. Generating the Relationship for the χ-rED Conversion Table

In-vivo brain imaging of a 27-year-old healthy volunteer was performed at Tohoku University Hospital using a 3.0-tesla MRI scanner (Trio Tim, SIEMENS Medical Systems, Erlangen, Germany) equipped with an 8-channel head coil. The T2-star-weighted images were acquired using a 3D gradient echo-based sequence with four different echo times, as well as the following parameters: number of echoes = 4; TEs = 9.5, 15.4, 21.3, and 27.3 ms, TR = 55 ms, flip angle = 15˚, FOV = 256 × 256 mm², matrix size = 256 × 256, slice thickness = 2 mm, number of slices = 64, pixel bandwidth = 241 Hz. These T2-star-weighted images were used to estimate the phase data. To estimate the local field map B_L(r), a Laplacian unwrapping of the phase [34] and a background field-removal PDF algorithm [29] were implemented to process phase data. Then, the magnetic susceptibility map, 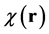, of the whole brain was reconstructed using the MEDI algorithm. These algorithms were implemented in Mathematica.

In addition, brain-CT images were acquired by dual-energy CT scanning using the same parameters employed in generating the 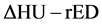conversion table. We obtained written informed consent before MR and CT imaging. Then,

these CT images were converted to rED using the conversion table.

The rED map was rigidly registered with the map and resampled to the magnetic susceptibility map’s resolution. Finally, the conversion table was obtained via voxel-by-voxel mapping between and rED map. Figure 3 shows a schematic used to generate the conversion table.

3. Results

3.1. Dual-Energy-Subtraction ΔHU − rED Conversion Table

Figure 4(a) shows the and plot with a straight line fitted using Equation (5). A magnified portion of the soft-tissue region between ±200 HU (the range ΔHU) is shown in Figure 4(b). The blue and green lines were acquired from high-and low-kV CT scans, respectively. The red line was acquired from Equation (5). The weighting factor, was set to 1.0, and the coefficient of determination, r², was 0.99 from the fitting process. The obtained a and b values of Equation (5) were 1.16 and 0.98, respectively. Table 1 lists the average HU values of each scan as well as the inserted material and the rED and values obtained using Equation (4). In Figure 4, with respect to the general curve, the blue and green lines create several segmented linear curves, and we assumed a linear relationship in each region. However, the curve could show a one-to-one linear relationship within a measured HU value range. Hence, we were able to generate a brain-rED map for voxel-by-voxel mapping between and rED without the effects from several segmented linear curves.

3.2. Magnetic Susceptibility Map from QSM in a Human Brain

Magnetic susceptibility maps reconstructed with a MEDI-algorithm method are

shown in Figure 5, which displays the magnitude images (Figure 5(a)) and map (Figure 5(b)). The magnetic susceptibility map represents values in ppm relative to that of water. The streaking artifacts of the dipole kernel were visible as rings in the front of the brain in the map (red arrow in Figure 5(b)). These strong artifacts were observed in some regions, such as the edge of brain and the periphery of sinus, and were caused by the large gradients of the magnetic susceptibilities. To remove the effects of these artifacts from the conversion table, we defined all values outside of the magnetic susceptibility range of ±1.0 ppm in the map as artifacts and excepted them from voxel- by-voxel mapping between and rEDmap. The measured mean magnetic susceptibility values in different brain regions are listed in Table 2, with the results of other reports utilizing the MEDI algorithm for QSM [35] .

Measured values in this study agreed with those of previous studies.

3.3. Generation of a Magnetic-Susceptibility-to-Relative-Electron-Density Conversion Table

Figure 6 shows the conversion table generated by voxel-by-voxel mapping between and rED. In healthy human brains, the main diamagnetic materials were caused by calcification and visualized as negative signals in QSM. Furthermore, the paramagnetic materials that mainly contributed to the magnetic-susceptibility values were iron contents, which were visualized as positive signal in QSM. The absolute largest magnetic-susceptibility values were in proportion to calcification or iron content, and those close to zero ppm were principally indicated by cerebrospinal fluid and brain matter containing microscopic diamagnetic or paramagnetic materials. The correlation coefficient between magnetic susceptibility and relative electron density was 0.0145.

4. Discussion

We investigated the feasibility of a method for generating a rED map from a

map obtained using MRI. In this study, we scanned the head of a healthy volunteer and attempted to convert the brain magnetic susceptibility to relative electron density. The magnetic susceptibility measured by QSM is determined by the molecular composition within an imaging voxel. Further, QSM can visualize the digitized true magnetic susceptibility and MR signals are generated by protons. Hence, magnetic susceptibility values obtained using QSM are influenced by the spatial variation in proton density and composition [36] . Furthermore, the number of electrons is proportional to the number of protons.MR quantitative values, such as magnetic susceptibility, T1, and T2, as well as magnitude images, such as T1- and T2-weighted images, are influenced by proton density. In this study, we evaluated the feasibility of QSM and magnetic susceptibility, which are relatively new techniques, as well as quantitative values as an imaging modality to obtain rED for MRI to perform only RTP. However, magnetic susceptibility and QSM contrast are determined by elements with strong susceptibilities, such as calcium and iron, and the influence of electrons on magnetic susceptibility and QSM contrast is very weak. Hence, no strong relationship between magnetic susceptibility and rED was obtained in the healthy volunteer’s head or in this study. If we had scanned avolunteer’s head containing calcification and attempted to convert magnetic susceptibility values to relative electron density, we might have been able to obtain a different relationship. The different brain regions, such as the globus pallidus, putamen, red nucleus, and caudate nucleus, display different magnetic susceptibility values because each region has a different iron content [26] [37] . When we used some parameters reported in previous research [37] , we were able to obtain the absolute iron content of each voxel from the map. Furthermore, we may be able to obtain the dose-to-medium reflected absolute iron content at each voxel. However, because the difference in the absolute iron content between each voxel is minute, even if we adjust the dose distribution to the absolute iron content, the small difference will be of little clinical significance. We obtained the map utilizing the optimization technique and multiecho gradient echo sequence. If we change the optimization or sequence parameters, we may obtain different maps. It is important to use the same optimization and sequence parameters for the repeatability of the data.

In QSM, diamagnetically and paramagnetically susceptible materials can be visualized as negative and positive, respectively. In previous studies, when we performed MRI-based radiotherapy planning or attenuation correction, GRE- magnitude images were often utilized to generate pseudo-CT images or contour- based segmented MRI images [38] [39] . GRE-magnitude images visualize diamagnetic calcification and paramagnetic cerebral hemorrhaging as a positive signal. Hence, we may fail to find appropriate segmentation or attenuation corrections when we use only GRE-magnitude images. However, if we utilize magnetic susceptibility map to make contour, we may be able to appropriate segmentation and attenuation corrections. In this study, we examined only one healthy volunteer’s head, and the brain tissue excluding the bone was evaluated to study the relationship between and rED. This is because strong artifacts were visualized on the brain surface in the map. If we scan the body trunk or pelvic regions, because bones such as the pelvic bone and femurs are located inside the body enough to avoid the artifacts, we may be able to obtain other relationships between and rED.

We utilized a conversion method to obtain a rED map from dual-energy CT scans. The generated conversion table has a high linearity. Our proposed conversion method has especial importance in the soft-tissue region (Figure 4(b)). If we used a general conversion method, the conversion table was subjected to the undesired effects of the segmented linear relationship the soft-tissue region. However, this undesired effect did not appear when we utilized the conversion table to generate the conversion table because this method offers high linearity in this region. The obtained conversion table contained residual errors between calculated and reference rED. In previous studies, researchers scanned a tissue characterization phantom with various scan parameters, particularly tube voltage, e.g., 80 - 140 kVp, 80 - 140 kVp with Sn filter, and 100 - 140 kVp [31] [32] , and generated the optimum conversion table. In this study, we scanned a phantom with clinical scan parameters (80 and 120 kVp) and obtained the conversion table without investigating the optimum scan parameters. If the conversion table is generated with optimum scan parameters, the residual error between calculated and reference rED may be smaller.

Some artifacts were observed in the magnetic susceptibility map in the peripheral sinus and at the edge of brain (Figure 5). In this study, we scanned the head of a healthy volunteer with MRI using the imaging parameters TEs = 9.5, 15.4, 21.3, and 27.3 ms. The TE value of 9.5 ms is relatively longer than those used in previous studies [21] [24] [35] . The QSM algorithms utilized the local magnetic field obtained from the phase data. Hence, obtaining accurate phase data was very important. However, our first scan time was 9.5 ms; this long first TE caused undesired dephasing and affected estimation of the local magnetic field. As a result, some artifacts were observed in the large-magnetic-suscepti- bility-gradient regions, such as the peripheral sinus and the edge of the brain. In spite of the presence of artifacts, the measured magnetic-susceptibility values of several deep-gray-matter regions in this study appeared approximately equivalent to their values in the literature [35] , and our QSM algorithm performed suitably at generating the magnetic susceptibility map. The difference in the magnetic-susceptibility values between this and the previous study may have been caused by some imaging parameters, such as voxel size, NEX, bandwidth, and the number of subjects. In contrast to our study that scanned one volunteer, the previous study scanned nine volunteers.

5. Conclusion

In this study, we attempted to generate a conversion table between magnetic susceptibility and relative electron density using the QSM algorithm and dual- energy CT scans. Correlations between magnetic susceptibility and relative electron density or CT number were not observed in the healthy volunteer’s head using our proposed method. Although magnetic susceptibility was strongly affected by iron content and calcification, neither the relative electron density nor the CT number were similarly affected. We evaluated our proposed method using only one healthy volunteer’s head. If we scanned more patients or other anatomical sites, such as the body trunk and pelvic regions, we may be able to obtain other relationships that were not acquired in this study; we aim to perform this in our future studies.

Acknowledgements

This work was supported by a JSPS KAKENHI Grant Number JP 15K19198.

Cite this paper

Ito, K., Kadoya, N., Nakajima, Y., Saito, M., Sato, K., Nagasaka, T., Yamanaka, K., Dobashi, S., Takeda, K., Matsushita, H. and Jingu, K. (2017) Feasi- bility of a Direct-Conversion Method from Magnetic Susceptibility to Relative Electron Density for Radiation Therapy Treatment Planning. International Journal of Medical Physics, Clinical Engineering and Radiation Oncology, 6, 252-265. https://doi.org/10.4236/ijmpcero.2017.63023

References