Open Journal of Energy Efficiency
Vol.3 No.1(2014), Article ID:43604,9 pages DOI:10.4236/ojee.2014.31003
The Identification of Peak Period Impacts When a TMY Weather File Is Used in Building Energy Use Simulation
Jay Zarnikau1,2*, Shuangshuang Zhu1
1Frontier Associates LLC, Austin, USA
2LBJ School of Public Affairs and Division of Statistics and Scientific Computing, The University of Texas at Austin, Austin, USA
Email: *jayz@frontierassoc.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 January 2014; revised 3 February 2014; accepted 11 February 2014
ABSTRACT
When typical meteorological year (TMY) data are used as an input to simulate the energy used in a building, it is not clear which hours in the weather data file might correspond to an electric or natural gas utility’s peak demand. Yet, the determination of peak demand impacts is important in utility resource planning exercises and in determining the value of demand-side management (DSM) actions. We propose a formal probability-based method to estimate the summer and winter peak demand reduction from an energy efficiency measure when TMY data and model simulations are used to estimate peak impacts. In the estimation of winter peak demand impacts from some example energy efficiency measures in Texas, our proposed method performs far better than two alternatives. In the estimation of summer peak demand impacts, our proposed method provides very reasonable results which are very similar to those obtained from the Heat Wave approach adopted in California.
Keywords:Peak Demand Reduction; Energy Efficiency Impact Analysis; Building Energy Use Simulation

1. Introduction
It is not always clear how weather-sensitive energy efficiency measures will perform at the exact hour(s) of the utility’s annual summer or winter system peak. Often, building energy use simulation models are used to obtain 8760 hourly impact estimates for the change in load associated with the efficiency measure based on typical meteorological year (TMY) data. TMY data contain actual months of weather data from different past years. Consequently, the TMY year does not coincide with any actual year and thus cannot be matched against actual demand or load data for a utility system or market. The hours associated with the most extreme temperatures in a TMY file may not necessarily correspond with a peak in demand in a utility system. Other factors, such as day of the week and the hour within the day, may also play a role. The challenge is to determine which of the 8760 hourly values obtained from a building energy use simulation model to select to represent the demand reduction at the time of the utility’s system peak.
This topic is of great importance to utility system planners. Electric and natural gas utility systems are constructed largely to meet peak demand. Thus, the impact or performance of an energy efficiency measure during peak periods is of keen interest. Energy efficiency measures or demand side management (DSM) programs are valued, in part, based upon the generation and transmission costs which they could potentially displace [1] . Thus, the potential for an energy efficiency measure to reduce demand during the system’s peak affects the value of measures and programs.
Various utility regulatory commissions in the US provide specific instructions for utilities and energy efficiency program administrators to follow when selecting the hour(s) associated with peak demand impacts. In California’s DEER database, “the demand savings due to an energy efficiency measure is calculated as the average reduction in energy use over a defined nine-hour demand period” [2] . These nine hours correspond with 2 pm to 5 pm during 3-day heat waves. The Mid-Atlantic Technical Reference Manual, used in Maryland, Delaware, and DC, states: “The primary way is to estimate peak savings during the most typical peak hour (assumed here to be 5 pm) on days during which system peak demand typically occurs (i.e., the hottest summer weekdays). This is most indicative of actual peak benefits.” [3] The New York Public Service Commission instructs: “Program Administrators (PAs) should calculate coincident peak demand savings based on the hottest summer non-holiday weekday during the hour ending at 5 pm.” [4] Wisconsin’s utility regulatory agency requires that peak demand reduction for weather-sensitive efficiency measures be based on average design-day conditions [5] . In Illinois, Colorado, New Jersey, and Maine, coincidence factors are used to estimate peak demand reduction based the impacts of a weather-sensitive efficiency measure on annual energy consumption [6] -[9] . For energy efficiency measures which are not weather-sensitive, a number of states find it acceptable to average the expected energy impacts of the measure over a large number of hours within some “peak period”. We are unaware of any regulatory authority having adopted a formal probabilistic approach to estimating the impacts of energy efficiency measures upon the peak demand of a utility or market.
A formal probabilistic approach is attractive because the system peak of a utility or a market may not necessarily coincide exactly with the hottest summer day, historical temporal patterns, design-day conditions, or heat waves. For example, an extremely hot summer temperature reading may not necessarily lead to a summer peak, if the extreme temperature occurs on a weekend (when energy use in the commercial or business sector may be lower) or early in the afternoon (before the occurrence of an after-work peak in household energy use). While extreme temperatures may be the most important determinant of system peak demand, various patterns in energy usage (as might be reflected by the time of day and the month of the year), and other factors may play a role as well. A probabilistic approach can be used to quantify how various factors may contribute to the establishment of a peak in system demand.
2. Proposed Approach
Our proposed approach to matching a seasonal peak on a utility system with a TMY data file involves the following steps:
Ÿ Establish the number of hours to be included in the set of peak hours to be predicted each year and season (e.g., summer and winter).
Ÿ Use a logistic regression model and hourly data for a number of historical years to estimate the relationship between setting a peak hour and a set of explanatory variables, including a temperature variable and dummy variables representing the time-of-day and month-of-year.
Ÿ Use the estimated relationships to assign marginal probabilities to changes in the explanatory variables.
Ÿ With the estimated relationships, calculate the probability of setting a peak hour based on TMY weather data.
Ÿ Find and average the savings (i.e., the difference between a base and change case) from the outputs of a building energy use simulation model that used the same TMY data file which corresponds to the same hours.
Although system planners often use a single hour or 15-minute interval to measure peak demand, predicting a larger set of peak hours tends to be more practical in the first step. Building energy use simulation models have stochastic algorithms. So if a single pair of model runs (i.e., a base case and a change case) is used to calculate hourly savings, the predicted savings may be biased for any single hour. So, either multiple model runs must be used to average the estimated hourly savings, or a broader definition of peak (i.e., peak hours) must be used. Further, in the analysis of the cost-effectiveness of energy efficiency measures and programs, the demand reduction tends to be valued based on the capital cost of a combustion turbine which normally has an expected annual runtime of 10 to 40 hours. Thus an analysis of the cost-effectiveness of energy efficiency measures and programs may benefit from knowledge of the impacts over a set of hours. Finally, estimating the probability of setting a set of peak hours is much easier than estimating a single peak hour or interval per year with a logistic model. For example, if six years of historical data are used and thus Y = 1 on only six instances, more advanced techniques would be required in the estimation (e.g., the use of a prior distribution and Bayesian estimation techniques) than those discussed here. For these reasons, a set of 20 peak hours is used in the examples presented here.
Note that the second step ignores many other very important factors that might affect the timing of the peak, including actions by industrial energy consumers and load-serving entities to respond to wholesale market price spikes1. The day of the week is also not considered. However, the inclusion of other variables would prevent the application of this approach when only a TMY weather file and a building energy use simulation model are used to calculate the peak demand reduction associated with an efficiency measure. TMY data are pieced-together from recorded weather during numerous previous years to create a typical year with typical fluctuations. Since the TMY data do not represent weather data from any single “real” year, there would be no way of matching “real” energy price data, the day of the week, or other variables to the fabricated weather data.
Marginal probabilities can be obtained by estimating a logistic regression or logit model [11] . Most statistical software packages can convert the results from a logit model into probabilities [12] [13] .
In the final step, either a simple average or a probability-weighted average (with the weights based on the probability of the seasonal peak being set in a particular hour in the TMY data file) could be used to estimate peak demand reduction among those hours within the set of peak demand hours.
3. An Example Determination of Peak Hours
An example is illustrated below to further explain the five steps described above. It is applied to the estimation of both summer and winter peak demand reduction associated with various energy efficiency measures.
Total system electrical load or demand in the Electric Reliability Council of Texas (ERCOT) electricity market is used in this example. The ERCOT electricity market is “settled” based on 15-minute intervals. There are 96 intervals in most days. Interval-level data were converted to hourly values to facilitate the estimation and provide a better match of load to hourly temperature data. The top 20 hours of each summer season of each year, Peak Hour, were coded 1, and all other hours were coded as 0. Variables representing the hours ending 16:00, 17:00, and 18:00 were included to capture time-of-day factors affecting electricity use. All hours before 2 pm and after 6 pm were assumed to have zero probability of being within the set of peak hours and were eliminated from the dataset to facilitate estimation. Additionally, two variables representing the month-of-year (July and August) were also included. Because summer peak loads are largely determined by air conditioning usage in Texas, a variable was constructed to represent the ratio between the actual temperature in a central location within the ERCOT market (Austin) for a given interval and the highest temperature reading during the given year (Relative Max Temp).
The resulting model was thus:
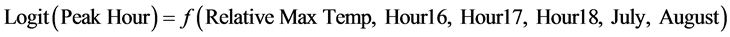 (1)
(1)
This relationship was estimated using R software as a general linear model with a binomial distribution. The estimated coefficients and p-values from the logistic regression are provided in Table 1.
Table 1. Logistic regression statistical results.
As we can see from Table 1, the coefficient estimates are significant at normally-accepted levels of statistical significance, with the possible exception of the dummy variable denoting the impact of the month of July (relative to the omitted months of June and September).
A unit increase in the relative maximum temperature-the ratio between the actual temperature in a central location within the ERCOT market (Austin) for a given interval and the highest temperature reading during the given year-raises the log of the odds of being included among the peak hours by 36.1022 ceteris paribus.
The coefficient estimate of 1.757 on the variable Hour 16 suggests that the log of the odds of the hour between 3:00 pm and 4:00 pm being among the peak hours (versus the 2:00 pm to 3:00 pm period or hour ending 15:00, the time period not explicitly represented in the model with a variable) is 1.757 time higher, holding all other variables constant. The log odds of setting a peak hour between 4:00 pm and 5:00 pm (Hour 17) versus setting a peak hour between 2:00 pm and 3:00 pm is 1.9924 times higher, holding other variables constant. Similarly, the log odds of the hour from 5:00 pm to 6:00 pm (Hour 18) being among the peak hours is 1.5439 times higher, relative to the omitted period and holding all other variables constant.
For the July and August variables, 0.9284 means the log odds of being a peak hour in July versus being a peak hour in June or September are 0.9284 times higher (which is actually a decrease), and the log odds of being a peak hour in August versus being a peak hour in June are 1.7722 times higher, confirming that summer peaks are most likely to occur in August in Texas.
The coefficient estimates expressed in log odds may be converted to odds ratios, by taking anti-logs.
Once the marginal probabilities are estimated, the probability of each hour of the TMY file being included among the set of peak hours can be calculated. As an example, consider an hour (3:00 pm to 4:00 pm, aka the hour ending 16:00) in August, with an hourly temperature of 100˚F, and the annual highest annual temperature being 102˚F. The estimated log of the odds ratio of being a peak hour versus being outside the set of peak hours:
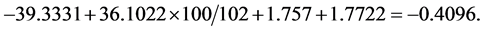
Thus the probability of obtaining a peak hour during that time and under those conditions is  This calculation may be performed automatically with R software.
This calculation may be performed automatically with R software.
The 20 hours in the TMY file assigned the highest probability of being within the set of peak hours are identified in Table 2. Our set of 20 peak hours consists of 7 hours in July and 13 hours in August, all falling within the 3:00 pm to 6:00 pm afternoon time period (i.e., the hours ending 16:00, 17:00, and 18:00). Certainly, temperature prominently determines the probability that an hour falls within the set of 20 peak hours. Yet, the TMY hour ending 17:00 on August 5, 2004 earns the third highest probability, despite having a lower temperature (98.06˚F) than some hotter hours (e.g., July 28, 1995 at 16:00 and 18:00). This is because the hour ending 17:00 is more likely to set a peak than the hours ending at 16:00 or 18:00. A probabilistic analysis appropriately takes into consideration both the weather and the time-of-day.
Having estimated the probability of each hour being included among the set of 20 peak hours in this section, we next demonstrate how this information may be used to estimate the impact of energy efficiency measures on peak electricity use when a building energy use simulation model is used to estimate hourly energy consumption using TMY data.
4. Matching the Selected Peak Hours to Energy Efficiency Savings Profiles
To estimate the impact of an energy efficiency measure upon peak demand, we match the hours with the highest
Table 2. Twenty peak hours with the highest probability of being included among the set of peak hours.
probability of being among the set of peak hours to those same hours in the output from a building energy use simulation model that used the same TMY data file. The average of the energy efficiency measure’s hourly savings over those 20 hours provides an estimate of the savings associated with the efficiency measure coincident with the summer peak.
Application of this approach to a simulation of the savings associated with ceiling insulation and air infiltration in an electrically-heated home in Austin is presented here. We also examine the savings from two lighting-related energy efficiency measures.
A whole-home simulation was developed using Energy Gauge, a simulation software tool that uses a DOE-2 simulation engine [14] . Prototype home characteristics were selected using available data on the construction, occupancy, and equipment characteristics of Texas homes, as listed in Table 3. The rows labeled “Ceiling Insulation” and “Air Infiltration” state the base and change conditions.
The simulations assumed differently sized HVAC systems for the analysis of the two weather-sensitive efficiency measures:
Ÿ Air infiltration: 2.8 ton air conditioning capacity, 3.5 ton heating capacity
Ÿ Ceiling Insulation: 4.3 ton air conditioning capacity, 4.8 ton heating capacity
Table 4 compares estimates of the demand reduction of various scenarios associated with our proposed probabilistic approach with some alternative methods2:
Ÿ Top 2 Hours of All Peak Months. Select the two hours when the peak hour has most-frequently occurred over the last ten years. Examine impacts during those two hours during every summer weekday during four summer months. Average the impacts over the resulting 170 hours—e.g., the hours ending 17:00 and 18:00 during every summer weekday.
Table 3. Home characteristics inputs used in simulation model.
Table 4. Summer peak demand reduction for various efficiency measures from different approaches.
Ÿ Heat Wave. The TMY weather files are scanned to locate a three-weekday period that has the highest average temperatures during the peak hours.
Ÿ Average Over Peak Period. Estimate a measure’s average impact between 1 pm and 7 pm on all summer weekdays over four summer months. (510 hours)
The second and third alternatives are consistent with the definitions adopted by some state regulatory authorities in the US, as discussed earlier in this paper. The Public Utility Commission of Texas formerly required the Average over Peak Period method. Note that two of these three methods ignore the weather information in the TMY file.
The peak demand reduction from two weather-sensitive efficiency measures, ceiling insulation type and air infiltration, is presented in Table 4. The estimated average summer demand reduction in Austin for a prototype home using the probabilistic analysis is 2.09 kW for the ceiling insulation efficiency measure and 0.34 kW for the air infiltration efficiency measure.
The demand reduction impacts of two non-weather-sensitive measures, indoor and outdoor lighting in Austin, have also been estimated. For indoor lighting kW savings, we assumed that 30% of the original usage would be saved if energy-saving indoor lighting equipment was installed. Thus an average of 0.062 kW savings could be calculated based on the Energy Gauge home simulation model during 20 summer peak hours. For outdoor lighting, we considered a variety of outdoor lighting equipment and assumed that 5 kW savings when the outdoor light is on is a reasonable deduction. Since none of the summer 20 peak hours occurs at night, the demand reduction associated with the outdoor lighting efficiency measure is 0 kW.
For the two weather-sensitive measures, the definitions involving the highest number of hours yield the smallest estimated peak demand reduction. This is a reasonable result, since including further hours (without regard to the temperature associated with those hours) into a calculation of average impacts shall lower the average and bias the results downward. Our proposed probabilistic method provides estimates which are very similar to the Heat Wave method for the summer. The impact of the indoor lighting efficiency measure is greatest under the Top 2 Hours of All Peak Months Definition.
Winter peak demand reduction estimates for our proposed approach can be implemented using steps similar to those described above. However, RelativeMaxTemp needs to be replaced by RelativeMinTemp to represent the ratio between the actual temperature in a central location within the ERCOT market (Austin) for a given interval and the lowest temperature reading during the winter in the year. A Heat Wave calculation is not performed for the winter peak. The winter kW savings estimated under three definitions appear in Table 5.
The probabilistic approach produces far higher (and more-realistic) winter peak impact estimates for the weather-sensitive efficiency measures. The wide difference in estimates using different approaches can be traced to Texas’ climate. Freezing temperatures set the winter peak and are a relatively rare event in this southern state. Deep freezes follow no predictable pattern. That is, one would not expect them to predictably occur during the same month-of-year and hour-of-day year after year. Consequently, the Top 2 Hours of All Peak Months performs poorly. Averaging over a prolonged winter peak period (in this case, from 6 am to 10 am and 6 pm to 10 pm) performs very poorly, as well, since many hours with mild temperatures and no need for space conditioning would be introduced into any peak period average.
All 20 of the winter peak hours happen after sunset and before sunrise. Consequently, the demand reduction in the winter for outdoor lighting is 5 kW under two of the three definitions. A lower peak demand reduction estimate is obtained when some daylight hours are included in the definition, as under the Average Over Peak Period calculation.
For indoor lighting, similar results are obtained under any of the approaches considered. For the weather-sensitive measures, the probability-based method provides far more-plausible results for a measure’s impacts on winter peak for Texas. Extreme temperatures indeed largely coincide with peaks in energy use, so the impacts of an efficiency measure during extreme weather (with adjustments for the time-of-day and month-of-year) should be used when estimating winter peak demand impacts. The use of simple temporal pat
Table 5. Winter peak demand reduction from different approaches.
terns which ignore temperatures or the averaging over large numbers of hours is inappropriate. It is suspected that in a colder climate where heat waves are a relatively rare event, the naïve application of patterns (without regard for temperature) or averaging to obtain summer peak impacts would similarly lead to implausible results.
5. Conclusions
Utility system planners and energy efficiency program administrators are interested in the impacts of energy efficiency programs at the time of peak demand on a utility system or energy market. Yet, it is not obvious which hour(s) correspond with peak hours when the output from a building energy use simulation model solved with TMY data is examined. Should the hour associated with the highest (or lowest) temperature be used? Should an average of the measure’s impacts during the hours and months within which the utility’s peak typically falls be used? Should impacts when design conditions are experienced be used? Should impacts during consecutive days of extreme weather be averaged? Would a lot of averaging dilute the impact of a weather-sensitive measure?
This paper proposes a formal probabilistic method to address this problem. We select the hours in a TMY weather data file most likely to coincide with a peak hour, based on the temperature, hour-of-day, and monthof-year data contained within the TMY data file and the relationships between these variables and actual load data for a utility system. Logistic regression is used to estimate the relationships based on actual historical data. The estimated relationships and TMY data are used to calculate the probability that an hour represented in the TMY data file would be included among a set of peak hours.
Our proposed approach represents a considerable improvement over existing practices which estimate impacts based solely on extreme temperatures in a TMY file, estimate impacts based upon design-day conditions, averages impacts over a large number of hours within a “peak period”, or relies upon typical times of peak occurrence without consideration of the temperature in the TMY file during those hours. When applied to data for Texas, a probability-based approach provides more-realistic estimates of winter peak impacts, relative to two alternatives. When estimating the impacts of an efficiency measure upon summer peak demand, our approach provides impacts similar to the Heat Wave approach being used in California.
References
- US Environmental Protection Agency (2006) National Action Plan for Energy Efficiency. US Environmental Protection Agency. http://www.epa.gov/cleanenergy/documents/suca/napee_report.pdf
- Itron, Inc. (2013) DEER Database: 2011 Update Documentation, Appendices. http://www.deeresources.com/files/DEER2011/download/2011_DEER_Documentation_Appendices.pdf
- Northeast Energy Efficiency Partnerships (2013) Technical Reference Manual, Version 3.0. http://www.neep.org/Assets/uploads/files/emv/emv-products/TRM_March2013Version.pdf
- New York Public Service Commission (2010) New York Standard Approach for Estimating Energy Savings from Energy Efficiency Programs: Residential, Multi-Family, and Commercial/Industrial Measures. http://www3.dps.ny.gov/W/PSCWeb.nsf/96f0fec0b45a3c6485257688006a701a/766a83dce56eca35852576da006d79a7/$FILE/TechManualNYRevised10-15-10.pdf
- Public Service Commission of Wisconsin (2010) Focus on Energy Evaluation, Business Programs: Deemed Savings, 2010. http://www.focusonenergy.com/sites/default/files/bpdeemedsavingsmanuav10_evaluationreport.pdf
- State of Illinois (2012) Energy Efficiency Technical Reference Manual. http://ilsagfiles.org/SAG_files/Technical_Reference_Manual/Illinois_Statewide_TRM_Version_1.0.pdf
- Xcel Energy (2012) 2012/2013 Demand Side Management Plan, Docket No. 11A-631EG. http://www.xcelenergy.com/staticfiles/xe/Marketing/Files/CO-DSM-2012-2013-Biennial-Plan-Rev.pdf
- New Jersey’s Clean Energy Program (2007) Protocols to Measure Resource Savings. http://www.njcleanenergy.com/files/file/Protocols_REVISED_VERSION_1.pdf
- Efficiency Maine (2013) Residential Technical Reference Manual. http://www.efficiencymaine.com/docs/EMT-TRM_Residential_v2014-1.pdf
- Zarnikau, J. and Thal, D. (2013) The Response of Large Industrial Energy Consumers to Four Coincident Peak (4CP) Transmission Charges in the Texas (ERCOT) Market. Utilities Policy, 26, 1-6. http://dx.doi.org/10.1016/j.jup.2013.04.004
- Train, K. (2003) Discrete Choice with Simulation. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511753930
- SAS Institute Inc. (1990) SAS/STAT User’s Guide, Vol. 1 & 2, Version 6. 4th Edition, SAS Institute Inc., Cary.
- Everitt, B. and Hothorn, T. (undated) A Handbook of Statistical Analyses Using R. http://cran.r-project.org/web/packages/HSAUR/vignettes/Ch_logistic_regression_glm.pdf
- Florida Solar Energy Center (undated) Energy Gauge. http://www.energygauge.com/
- US Department of Energy (2009) Energy Information Administration, Residential Energy Consumption Survey (RECS). http://www.eia.gov/consumption/residential/
- Lawrence Berkeley National Laboratory. Residential Diagnostics Database. http://resdb.lbl.gov/
- Lawrence Berkeley National Laboratory. RESFEN. http://windows.lbl.gov/software/resfen/resfen.html
NOTES

*Corresponding author.

1An application of this probabilistic method in a situation where utility load data can be matched with actual weather and actual electricity prices can be found in . These alternative proposed approaches are adopted from .

3These alternative proposed approaches are adopted from .


