Advances in Breast Cancer Research
Vol.2 No.4(2013), Article ID:36729,7 pages DOI:10.4236/abcr.2013.24020
Parametric Cure Model versus Proportional Hazards Model in Survival Analysis of Breast Cancer and Other Malignancies
1Tenri Institute of Medical Research, Tenri, Japan
2Department of Ophthalmology, University of Louisvill, Louisville, USA
Email: *maetani@tenriyorozu.jp
Copyright © 2013 Shunzo Maetani, John W. Gamel. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 7, 2013; revised July 8, 2013; accepted July 15, 2013
Keywords: Cancer Survival Analysis; Boag Model; Cox Model; Cure
ABSTRACT
As cancer therapy has progressed dramatically, its goal has shifted toward cure of the disease (curative therapy) rather than prolongation of time to death (life-prolonging therapy). Consequently, the proportion of cured patients (c) has become an important measure of the long-term survival benefit derived from therapy. In 1949, Boag addressed this issue by developing the parametric log-normal cure model, which provides estimates of c and m where m is the mean of log times to death from cancer among uncured patients. Unfortunately, traditional methods based on the proportional hazards model like the Cox regression and log-rank tests cannot provide an estimate of either c or m. Rather, these methods estimate only the differences in hazard between two or more groups. In order to evaluate the long-term validity and usefulness of the parametric cure model compared with the proportional hazards model, we reappraised randomized controlled trials and simulation studies of breast cancer and other malignancies. The results reveal that: 1) the traditional methods fail to distinguish between curative and life-prolonging therapies; 2) in certain clinical settings, these methods may favor life-prolonging treatment over curative treatment, giving clinicians a false estimate of the best regimen; 3) although the Boag model is less sensitive to differences in failure time when follow-up is limited, it gains power as more failures occur. In conclusion, unless the disease is always fatal, the primary measure of survival benefit should be c rather than m or hazard ratio. Thus, the Boag lognormal cure model provides more accurate and more useful insight into the long-term benefit of cancer treatment than the traditional alternatives.
1. Introduction
In recent decades, as more cancer victims have enjoyed long-term, relapse-free survival, cure has become a reality for both patients and clinicians. Thus, the primary goal of cancer therapy has shifted toward cure of the disease rather than prolongation of time to death. To achieve a cure, selecting the best regimen is vital. This is especially true with children, for whom curative treatment can yield many years of healthy life, while prolongation of life offers only a limited benefit before relapse takes the child’s life. Furthermore, cured patients are saved from cancer-associated sufferings, which could be more unbearable to patients than death itself. Hence, the proportion of cured patients (cure rate) has become an important measure of long-term survival benefit.
As early as 1949, Boag [1] addressed this issue by developing a parametric cure model that allowed him to estimate the cure rate (c) and the mean of log failure times (m) among uncured patients (failure time means time to death from cancer under study). Twenty-three years later, Cox [2] published the proportional hazards model, which uses the hazard ratio to measure the survival difference between groups. Since then non-parametric or semi-parametric methods based on his model (e.g., log-rank test and Cox regression) have remained the mainstay of cancer survival analysis. Hereafter these methods will be referred to as “standard survival analysis”. The purpose of our paper is to compare the usefulness of the Boag and Cox models, whose primary parameters are the cure rate and the hazard ratio, respectively, and also to confirm the validity of the Boag model using the data from breast cancer and other neoplastic diseases.
2. Survival Models and Results of Their Applications
2.1. Proportional Hazards Model
In 1972, Cox [2] developed a unique model, paying special attention to the hazard, which is the probability that survivors at the beginning of a unit interval will die during that interval. He assumed that at any point in time the hazard in one group is proportional to the hazard in a second group at the same time point. It is important to note, however, that the absolute hazard may vary over time while the hazard ratio (HR) between the two groups remains constant. This single constant allows us to compare survival between groups. For example, if the average HR between the two groups is 0.5, it is presumed that the mortality in one group is one half of the mortality in the other group.
2.2. Relationship between Cure Rate and Hazard Ratio
It is generally assumed that, provided the proportional hazards model holds, the proportion of patients cured (i.e., saved from the event) can be estimated by 1-HR [3-5], which in turn is calculated from standard survival analysis. For example, consider a trial that compared adjuvant chemotherapy with or without trastuzumab and found a HR of 0.67 in HER2-positive breast cancer patients [6]. This result can be summarized either as “trastuzmab therapy is associated with a 33% (= 1 − 0.67) reduction in the risk of death”, or as “trastuzumab therapy prevents 33% of the deaths that would occur without the therapy”. Such statements are commonly found in leading medical journals [3,4,6,7]. Hence, given this information, most patients would believe their chance of being cured could be increased with the treatment if it shows a HR less than 1.
However, according to Peto et al. [8] and Clark et al. [9], 1-HR is not the proportion of patients whose deaths (or relapse) are prevented by treatment, but the proportion of deaths that are either prevented or delayed. Thus, as will be seen, the HR cannot distinguish between treatments that prevent death (curative treatment) and those that merely delay it (life-prolonging or death-delaying treatment).
Moreover, the relationship between the cure rate and HR became even more questionable when we read the Cox original paper [2], where he used the data from the Acute Leukemia Group B [10] as an example. Between 1959 and 1960, this group had conducted a randomized controlled trial to estimate the effect of 6-mercaptopurine (6-MP) versus placebo on steroid-induced remission of patients with acute leukemia (most were children with acute lymphoblastic leukemia).
When we re-analyzed the data using the Cox model, the HR of 6-MP versus placebo was 0.22 (95% CI: 0.10 to 0.49) [11]. If the relationship between the cure rate and HR were valid, this finding would indicate the following: 78% (1-HR = 100% - 22%) of the relapse that would have occurred in the placebo group were prevented by 6-MP. On the contrary, further follow-up of 6-MP-treated children revealed that almost all died from relapse [12,13].
Although the Cox model is still commonly used in cancer survival analysis, Cox [14] himself acknowledged the limitations of his model. More specifically, he stated that the model is unlikely to achieve the two objectives: 1) long-term survival study decoupled from shorter-term effects; and 2) provision of patient-specific prognostic information for clinician and an individual patient.
2.3. Parametric Cure Model
The Boag log normal model incorporates the cure rate as one of its parameters [1]. He assumed that a fraction (c) of the patients with a specific cancer are cured of the disease by treatment, while the remaining incurable patients will eventually die of the disease (Figure 1) unless they succumb to other causes. He further assumed that log failure times among uncured patients follow a normal distribution with mean (m) and standard deviation (s). In the era when computers were not available, Boag manually estimated these three parameters for various tumors such as cancers of the breast, uterus, lung, head and neck, etc.
In 1977, Farewell [15] modeled the parameter c as a dependent variable in a logistic regression, while in 1994 Gamel and McLean [16] expressed all three parameters of the Boag model as multivariate regressions on various covariates. This allows clinicians to determine the effects of treatment and other prognostic factors on both c and m—information that cannot be obtained with the hazard ratio in the Cox model.
The multivariate model was then extended to allow the analysis of grouped data where information on the cause of death for individual patients may not be available [17,18] (http://survillance.cancer.gov/cansurv/).
When the nultivariate Boag model was applied to the 6 MP data, we found that the chemotherapy failed to cure the disease (Wald P = 0.99), but rather prolonged time to relapse 3.8 times longer (95% CI: 2.07 to 7.15) than in the placebo group [11]. However, since 1960 the proportion of clinically cured children with acute lymphoblastic leukemia has steadily increased to 80% due to progress in anticancer regimen (Figure 2) [19].
These results show that at least two types of anticancer treatments are available: a curative one that increases the
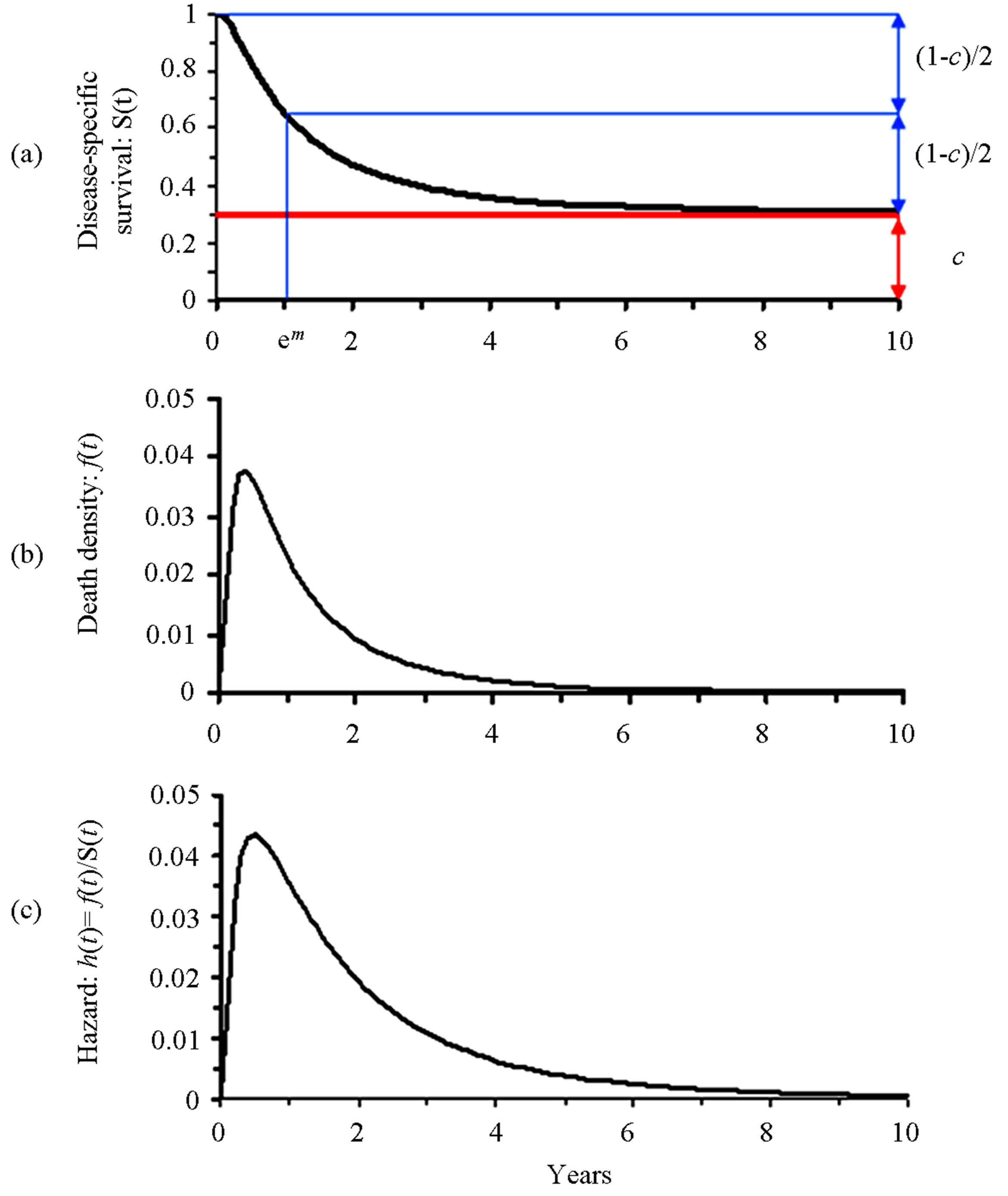
Figure 1. Three curves derived from the Boag model. c: cure rate; m: mean log failure time; em: median failure time.
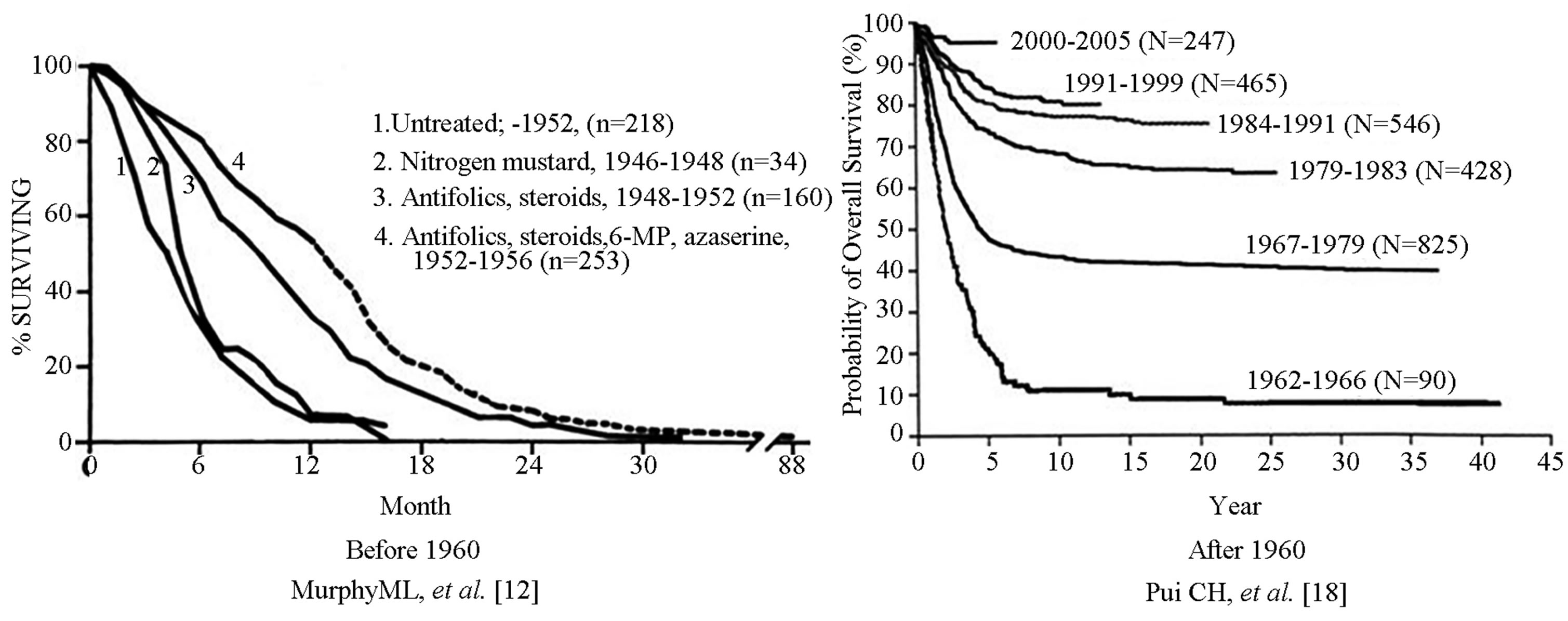
Figure 2. Results of chemotherapy for childhood acute lymphoblastic leukemia before and after 1960. By permission of Pediatric Clinic of North America and New England Journal of Medicine.
fraction of patients cured of the disease and a life-prolonging one that merely delays tumor-related death. To illustrate the differential effects of these two regimens on survival and hazard curves, these curves were simulated by increasing one of the two parameters (either c or m) of the Boag model (Figure 3).
The red curves show the base-line values of the control group (Group 1), while the blue curves represent the effects of therapies (Group 2). The middle and right panels show the effects of curative and life-prolonging regimens, respectively.
It is readily seen that increase in parameter m alone

Figure 3. Survival and hazard curves derived from the Boag model and Cox model. Red: control (Group 1); blue: test treatment (Group 2); c: cure rate; m and s: mean and standard deviation of log failure times in month. To meet the Cox proportional hazard assumption, non-mixture model29 was used (left side panels). Thus, the survival rates were estimated as cF(t), where c represents the cure rate; F(t) the cumulative lognormal distribution, and the hazard rate is estimated as ln(c) F(t) .
from 2.5 to 3.0 results in crossing of the hazard curves (right lower panel), so the proportional hazards assumption does not hold. The left panels show the survival and hazard curves satisfying the proportional hazards assumption. Note that these curves are very similar to the corresponding ones derived from the Boag model (middle panels) in which the parameter c alone is increased from 0.3 to 0.4 while m is kept unchanged.
2.4. Cox Model versus Boag Model in Randomized Controlled Trials of Cancer Therapy
To further illustrate the difference between these models, two examples of randomized controlled trials will be shown in which both models are applied.
2.4.1. Effect of Adjuvant Chemotherapy for Stage 2 Breast Cancer
Using the three parametric versions of the Boag cure model (lognormal, log logistic and Weibul) plus the log-rank statistic, Gamel et al. [20] re-analyzed the data from five randomized controlled trials. These trials, published from 1981 to 1992 by Bonadona et al. evaluated adjuvant chemotherapy for stage 2 breast cancer [21-25]. The chemotherapeutic regimens included standard treatment (i.e., mastectomy alone) or mastectomy plus intravenous CMF (cyclophosphamide, methotrexate and fluouracil) with or without doxorubicin.
The results showed that in three of the five trials there were statistically significant survival differences between the treatment and control groups. However, a curative effect was found only in the trial with doxorubicin plus CMF, whereas in the other two positive trials (with CMF regimens), the treatment merely prolonged the time to relapse. The stepwise log likelihood ratio test and chi-square statistics showed that the lognormal distribution provided the better fit to the pooled data than the log-logistic or Weibul versions of the Boag cure model.
2.4.2. Effect of D2 versus D1 Lymphadenectomy in Gastric Resection for Cancer
From 1989 to 1993, the Dutch Gastric Cancer Group [26] conducted a randomized controlled trial to compare the effects of limited lymphadenectomy (D1) versus extended lymphadenectomy (D2) in 711 patients undergoing potentially curative gastrectomy for gastric adenocarcinoma. After a median follow-up of 6 years the hazard ratio for relapse between D2 and D1 groups was 0.84 (95% CI: 0.65 to 1.09). These findings suggest no significant difference, whereas the postoperative mortality and morbidity were significantly higher with D2 dissection.
Such negative results did not agree with the clinical experience of Japanese surgeons, so we applied the Boag model to the same data. Our findings showed a significant difference in cure rate (11.5%; 95% CI: 3.1 to 20.0)
between the two groups [11]. Later the Dutch group, by extending their follow-up to a median of 15 years, found that D2 lymphadenectomy is associated with a significantly lower disease-related death rate (37% versus 48%) with a hazard ratio of 0.74 (95% CI:0.59 to 0.93) [27]. This difference in the death rate (11%) is close to the difference in cure rate (11.5%) found with the Boag model approximately 10 years earlier.
3. Discussion
Boag is the first scientist who attached special importance to cure in the analysis of cancer-related survival. The multivariate extension of his model estimates the impact of treatment and other prognostic variables on the likelihood of cure, thus providing both patients and clinicians the information they need to make vital decisions [28]. Although the hazard ratio in the Cox model is closely related to the cure rate in the Boag model [29], HR is less comprehensible to non-statisticians than c, which more accurately depicts the long-term survival benefit of a given treatment.
In contrast, the parameter m of the Boag model plays a subordinate role unless all patients being studied are incurable. If only time to death is studied to assess the effect of treatment, this could be likened to counting only the coins in a cash transaction while leaving the bills uncounted.
Clinical trials and simulation studies have shown that standard survival analysis suffer a number of failings; 1) they cannot distinguish between curative and life-prolonging treatments [21,30,31]; 2) they are more sensitive to an increase in failure time than to an increase in cure rate, especially when the follow-up is limited; 3) as a result, they may favor a death-delaying treatment over one that is curative; 4) they tend to loose power with increasing follow-up [30,32,33].
These limitations are graphically shown in Figure 3. In the right lower panel, the two hazard curves representing the control (red) and the test treatment (blue), respectively, separate at the beginning, but then come closer and cross. If follow-up is truncated earlier than this crossing (for example, at 2 years), the hazard curve of the life-prolonging treatment remains lower than that of the control throughout the study. Thus the HR of treatment versus control would be overstated, while violation of the proportional hazards assumption may be missed. For these reasons, standard analysis might mislead clinicians and patients into selecting a less effective regimen. Though pharmaceutical industries may benefit from the consumption of such drugs, the welfare of patients and their families will suffer; if they were correctly informed, they might have refused to have a regimen that merely delays death. When Heyland et al. [34] interviewed 278 elderly patients who were at high risk of dying in the next 6 months. Only 12% preferred life-prolonging care.
On the other hand, the parametric cure models also suffer limitations. They are less sensitive to difference in failure time during the early period [31], although they gain power with longer follow-up. Furthermore, under certain conditions, they may provide a poor fit to the observed data. To avoid this problem, some statisticians recommend alternative parametric models.
However, the cause of the poor fit may not be use of the wrong model (misspecification) but misclassification of events. For example, patients who actually died from therapeutic complications in the early postoperative period may be misclassified as dead from cancer (failure). It must be kept in mind, however, that early failure is very rare, since most clinical trials in the adjuvant setting require that participants are in remission or have undergone potentially curative surgery (i.e., these are the eligibility criteria for candidates to be enrolled in the trial). So it is unlikely that failure occurs shortly after its cause has been eliminated.
Even if the trial is conducted in the non-adjuvant setting, imminently fatal cases should have been excluded from most trials. Consequently, the actual hazard curve should begin at zero, rise to a peak and then gradually decline to zero (Figure 1). Such a unimodal hazard curve is seen only in the lognormal or log-logistic model, but not in the Weibul or gamma model. If death occurs very early, the cause of death should be checked carefully. If the cause is ambiguous, such cases should be classified as censored at the time of death. Otherwise, the maximum likelihood estimation may fail to converge, or the result may be biased toward a shorter estimate of m.
Another criticism against the parametric cure models is that they rely on “extrapolation of a survival curve outside the available data” [5,35]. It is important to note, however, that predicting events beyond observed data has long served many branches of sciences. An excellent example is meteorology, where predicting the course of hurricanes has enjoyed great success. In addition, few models have been reported to provide a better fit to observed survival data than the lognormal or loglogistic models [1,20,35-39]. Nevertheless, we must continue our effort to find a better model using large, accurate, lifelong follow-up data sets.
4. Conclusion
In conclusion, unless the disease is always fatal, the primary measure of survival benefit should be the proportion of patients cured rather than hazard ratio or median time to failure. Thus, the Boag lognormal cure model provides more accurate and more useful insight into the long-term benefit of cancer treatment than the standard non-parametric alternatives.
REFERENCES
- J. W. Boag, “Maximum Likelihood Estimates of the Proportion of Patients Cured by Cancer Therapy,” Journal of the Royal Statistical Society: Series B (Methodological), Vol. 11, No. 1, 1949, pp. 15-53.
- D. R. Cox, “Regression Models and Life-Table,” Journal of the Royal Statistical Society: Series B (Methodological), Vol. 34, No. 2, 1972, pp. 187-220.
- R. D. Gelber and A. Goldhirsh, “Reporting and Interpreting Adjuvant Therapy Clinical Trials,” Journal of the National Cancer Institute: Monographs, No. 11, 1992, pp. 59-69.
- D. Sargent, A. Sobrero, A. Grothey, M. J. O’Connell, M. Buyse, et al., “Evidence for Cure by Adjuvant Therapy in Colon Cancer: Observations Based on Individual Patient Data from 20, 898 Patients on 18 Randomized Trials,” Journal of Clinical Oncology, Vol. 27, No. 6, 2009, pp. 812-877. http://dx.doi.org/10.1200/JCO.2008.19.5362
- X. Paoletti and B. Asselain, “Surgical Analysis in Clinical Trials: Old Tools or New Techniques,” Surgical Oncology, Vol. 19, No. 2, 2010, pp. 55-58. http://dx.doi.org/10.1016/j.suronc.2010.01.004
- E. Romond, E. A. Perez, J. B. Bryant, V. J. Surman, V. J. Suman, et al., “Trastzumab plus Adjuvant Chemotherapy for Operable HER-Positive Breast Cancer,” The New England Journal of Medicine, Vol. 353, 2005, pp. 1673- 1684. http://dx.doi.org/10.1056/NEJMoa052122
- L. G. Gianni, W. Eiermann, V. Semiglazov, A. Manikhas, A. Lluch, et al., “Neoadjuvant Chemotherapy with Trastuzumab Followed by Adjuvanttrastuzumab versus Neoadjuvant Chemotherapy Alone, in Patients with HER2- Positive Locally Advanced Breast Cancer (the NOAH Trial): A Randomized Controlled Superiority Trial with a Parallel HER2-Negative Cohort,” Lancet, Vol. 375, No. 9712, 2010, pp. 377-384. http://dx.doi.org/10.1016/S0140-6736(09)61964-4
- R. Peto, M. C. Pike, P. Armitage, N. E. Breslow, D. R. Cox, et al., “Design and Analysis of Randomized Clinical Trials Requiring Prolonged Observation of Each Patient: Part 2. Analysis and Examples,” British Journal of Cancer, Vol. 35, 1977, pp. 1-39. http://dx.doi.org/10.1038/bjc.1977.1
- T. G. Clark, M. J. Bradburn, S. B. Love and D. G. Altman, “Survival Analysis Part I: Basic Concepts and First Analyses,” British Journal of Cancer, Vol. 89, 2003, pp. 232-238. http://dx.doi.org/10.1038/sj.bjc.6601118
- E. J. Freireich, E. Gehan, E. Frei, et al., “The Effect of 6-Mercaptopurine on the Duration of Steroid-Induced Remission in Acute Leukemia: A Model for Evaluation of Other Potentially Useful Therapy,” Blood, Vol. 21, No. 6, 1963, pp. 699-716.
- S. Maetani and J. W. Gamel, “Paranetric Cancer Survival Analysis Using the Boag Model: A Clinician’s View,” Journal of Biometrics & Biostatistics, Vol. 3, 2012, p. 3. http://dx.doi.org/10.4172/2155-6180.1000140
- M. L. Murphy, “Leukemia and Lymphoma in Children,” Pediatric Clinics of North America, Vol. 6, No. 1, 1959, pp. 611-638.
- G. J. D’angio and T. J. Vietti, “Old Man River: The Flow of Pediatric Oncology,” Hematology/Oncology Clinics of North America, Vol. 15, No. 4, 2001, pp. 599-607. http://dx.doi.org/10.1016/S0889-8588(05)70238-0
- D. R. Cox, “Summary Comments on Evolution of Cancer Survival Analysis,” Surgical Oncology, Vol. 19, No. 2, 2010, p. 61. http://dx.doi.org/10.1016/j.suronc.2010.04.001
- V. T. Farewell, “A Model for a Binary Variable with Time-Censored Observations,” Biometrika, Vol. 64, No. 1, 1977, pp. 43-46. http://dx.doi.org/10.1093/biomet/64.1.43
- J. W. Gamel and I. W. McLean, “A Stable, Multivariate Extension of the Log-Normal Survival Model,” Computers and Biostatistical Research, Vol. 27, No. 2, 1994, pp. 148-155. http://dx.doi.org/10.1006/cbmr.1994.1014
- J. W. Gamel, E. A. Weller, M. N. Wesley, et al., “Parametric Cure Models of Relative and Cause-Specific Survival for Grouped Survival Times,” Computer Methods and Programs in Biomedicine, Vol. 61, No. 2, 2000, pp. 90-110. http://dx.doi.org/10.1016/S0169-2607(99)00022-X
- B. Yu, R. C. Tiwari, K. A. Cronin, et al., “CANSURV: A Windows Program for Population-Based Cancer Survival Analysis,” Computer Methods and Programs in Biomedicine, Vol. 80, No. 3, 2005, pp. 195-203. http://dx.doi.org/10.1016/j.cmpb.2005.08.002
- C. H. Pui, W. E. Evans and D. Pharm, “Treatment of Acute Lymphoblastic Leukemia,” The New England Journal of Medicine, Vol. 354, 2006, pp. 166-178. http://dx.doi.org/10.1056/NEJMra052603
- J. W. Gamel, R. L. Vogel, P. Valagussa and G. Bonadonna, “Parametric Survival Analysis of Adjuvant Therapy for Stage II Breast Cancer,” Cancer, Vol. 74, No. 9, 1994, pp. 2483-2490. http://dx.doi.org/10.1002/1097-0142(19941101)74:9<2483::AID-CNCR2820740915>3.0.CO;2-3
- G. Bonadonna and P. Valagussa, “Dose-Response Effect of Adjuvant Chemotherapy in Breast Cancer,” The New England Journal of Medicine, Vol. 304, 1981, pp. 10-15. http://dx.doi.org/10.1056/NEJM198101013040103
- G. Tancini, G. Bonadonna, P. Valagussa, S. Marchini and U. Veronesi, “Adjvant CMF in Breast Cancer: Comparative 5-Year Results of 12 versus 6 Cycles,” Journal of Clinical Oncology, Vol. 1, No. 1, 1983, pp. 2-10.
- R. Buzzoni, G. Bonadona, P. Valagussa and M. Zambetti, “Adjuvant Chemotherapy with Doxorubicin plus Cyclophosphamide, Methotrexate, and Fluorouracil in the Treatment of Respectable Breast Cancer with More than Three Positive Axillary Nodes,” Journal of Clinical Oncology, Vol. 9, No. 12, 1991, pp. 2134-2140.
- A. Moliterni, G. Bonadonna, P. Valagussa, L. Ferrari and M. Zambetti, “Cyclophosphamide, Methotrexate, and Fluouracil with and without Doxorubicin in the Adjuvant Treatment of Respectable Breast Cancer with One to Three Positive Axillary Nodes,” Journal of Clinical Oncology, Vol. 9, No. 7, 1991, pp. 1124-1130.
- M. Zambth, G. Bonadonna, P. Valagussa, et al., “Adjuvant CMF for Node-Negative and Estrogen ReceptorNegative Breast Cancer,” J Natl Cancer Inst Monogr, Vol. 11, No. 1, 1992, pp. 79-85.
- J. J. Bonenkamp, J. Hermans, M. Sasako, et al., “Extended Lymphnode Dissection for Gastric Cancer,” The New England Journal of Medicine, Vol. 340, No. 12, 1999, pp. 908-914. http://dx.doi.org/10.1056/NEJM199903253401202
- I. Songun, H. Putter, E. M. Kranenbarg, M. Sasako and C. J. van de Velde, “Surgical Treatment of Gastric Cancer: 15-Year Follow-Up Results of the Randomized Nationwide Dutch D1D2 Trial,” Lancet Oncology, Vol. 11, No. 5, 2010, pp. 439-449. http://dx.doi.org/10.1016/S1470-2045(10)70070-X
- J. L. Haybittle, “Life Expectancy as a Measurement of the Benefit Shown by Clinical Trials of Treatment for Early Breast Cancer,” Clinical Oncology, Vol. 10, No. 2, 1998, pp. 92-94. http://dx.doi.org/10.1016/S0936-6555(05)80485-6
- R. Sposto, “Cure Model Analysis in Cancer: An Application to Data from Children’s Cancer Group,” Statistics in Medicine, Vol. 21, No. 2, 2002, pp. 293-312. http://dx.doi.org/10.1002/sim.987
- J. W. Gamel, R. L. Vogel and I. W. McLean, “Assessing the Impact of Adjuvant Therapy on Cure Rate for Stage 2 Breast Carcinoma,” British Journal of Cancer, Vol. 68, 1993, pp. 115-118. http://dx.doi.org/10.1038/bjc.1993.296
- J. W. Gamel and R. L. Vogel, “Comparison of Parametric and Non-Parametric Survival Methods Using Simulated Clinical Data,” Statistics in Medicine, Vol. 16, No. 14, 1997, pp. 1629-1643. http://dx.doi.org/10.1002/(SICI)1097-0258(19970730)16:14<1629::AID-SIM594>3.0.CO;2-C
- P. Frankel and J. Longmate, “Parametric Models for Accelerated and Long-Term Survival: A Comment on Proportional Hazards,” Statistics in Medicine, Vol. 21, No. 21, 2002, pp. 3279-3289. http://dx.doi.org/10.1002/sim.1273
- S. Maetani, Y. Segawa, H. Banja, et al., “Simulation of Randomized Controlled Trials for Cancer Therapy Using the Boag Model and the Competing Risk Model,” Tenri Medical Bulletin, Vol. 11, No. 1, 2008, pp. 23-48.
- D. K. Heyland, D. Barwich, D. Pichora, et al., “Failure to Engage Hospitalized Elderly Patients and Their Families in Advance Care Planning,” JAMA Internal Medicine, Vol. 173, No. 9, 2013, pp. 778-788.
- R. Sposto, “Commentary on Paper, ‘Cancer Survival Analysis’,” Surgical Oncology, Vol. 19, No. 2, 2010, pp. 59-60. http://dx.doi.org/10.1016/j.suronc.2010.04.002
- J. W. Berg, “Disease-Oriented End Results: A Tool for Pathological-Clinical Analysis,” Cancer, Vol. 17, No. 6, 1964, pp. 693-707. http://dx.doi.org/10.1002/1097-0142(196406)17:6<693::AID-CNCR2820170603>3.0.CO;2-F
- R. F. Mould and J. W. Boag, “A Test of Several Parametric Statistical Models for Estimating Success Rate in the Treatment of Carcinoma Cervix Uteri,” British Journal of Cancer, Vol. 32, 1975, pp. 529-550. http://dx.doi.org/10.1038/bjc.1975.259
- R. F. Mould, T. Hearnden, M. Palmer and G. C. White, “Distribution of Survival Times of 12,000 Head and Neck Cancer Patients Who Died with Their Disease,” British Journal of Cancer, Vol. 34, 1976, pp. 180-190. http://dx.doi.org/10.1038/bjc.1976.141
- L. E. Rutqvist, A. Wallgren and B. Nilsson, “Is Breast Cancer a Curable Disease? A Study of 14,731 Women with Breast Cancer from the Cancer Registry of Norway,” Cancer, Vol. 53, No. 8, 1984, pp. 1793-1800. http://dx.doi.org/10.1002/1097-0142(19840415)53:8<1793::AID-CNCR2820530832>3.0.CO;2-Y
NOTES
*Corresponding author.

