ABSTRACT

During the last subprime mortgage crisis, the concentration risk issue has become increasingly important in the world of finance. This risk is defined as the loss that we can incur from a large exposition of a single name counterparty, a sector or a product. This paper represents some mathematical models for assessment and quantification of the concentration risk under the Add-On approach. This study is based on the Granularity Adjustment (GA). This measure quantifies the idiosyncratic risk that is neglected by the Asymptotic Single Risk Factor model (ASRF) based on the infinitely granular assumption of the portfolio. This work is about the approximation of this measurement to simplify the formula of GA using the Ad-Hoc approach. We have implemented empirical tests to find the relation between the GA and concentration indexes and we applied these results to the iBoxx portfolio.

Keywords:

Credit Risk, Asymptotic Single Risk Factor, Concentration Risk, Granularity Adjustment, Vasicek Model, Credit Risk+ Model

1. Introduction

The Ad-Hoc approach does not take into consideration the specific risk factors like the PD and LGD. On the other hand, it does not allow computing the provision charge of capital requirement to cover the concentration risk. Behind this, the GA represents all specific risks neglected by the ASRF model, so it’s over than the concentration risk. However, we can use it as a metric to measure this kind risk.

This paper studies the modeling and the approximation of this measure of concentration risk. We will focus on the credit environment that represents the banking book and the source of risks in the bank balance. We will restrict on the name concentration.

First, we will begin by modeling the name concentration under the granularity adjustment. Next, we will implement this approach in the Vasicek and Credit Risk+¹ models. Then, we will suggest the approximation of the GA. Finally, we will implement some tests to see the efficiency of these approximations and we will use these results on the iBoxx portfolio to make it available.

2. The Formulation of Granularity Adjustment (GA)

The GA was developed to underpin the Asymptotic Single Risk Factor model (ASRF) in order to cover the idiosyncratic risk under Internal Rating Based model (IRB) of Basel II. Indeed, the ASRF model supposes that the portfolio is infinitely granular and this assumption neglected the specific risk. The GA formula was computed by Wilde (2001) . Thereafter, Martin and Wilde (2002) used the results of Gourieroux et al. (2000) to simplify it. In this section, we will compute the GA formulation under the Vasicek and Credit Risk+ models. We deem X as the one-dimensional systematic factor and as the portfolio loss with N loan, and giving the following notations of the mean and the variance of the conditional loss²:

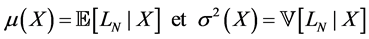
For, the portfolio loss is equal to:

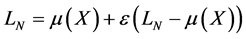
Using these notations, the GA is defined as:

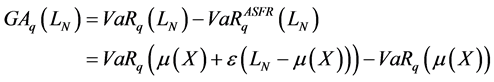
By applying the Taylor expansion on with second order according to the 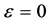and by replacing the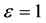, we get³:

By computing the first and the second derivative terms, we find the following results⁴:

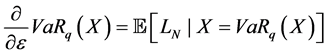
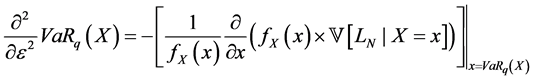
With defines the density function of X.

If we set, we get the following results⁵:

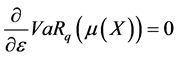
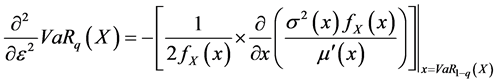
We find the general formula of GA basing on these results:

Therefore, if we want to explain this formula we should use a risk model. The most prevalent models for the banking book to calculate the capital request for the credit risk is: The Vasicek and the Credit Risk+ models. The first one is deemed as a structural model, and the second one belongs to the intensity model. In the following paragraphs, we will develop the GA formula under these models.

・ The GA formula under the Vasicek model:

The Vasicek⁶ model supposes that the systematic factor is following the Gaussian distribution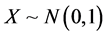, and this result leads to:

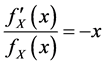
Substituting in the formula of GA, we get:

Thus, we can compute the components that allow computing the GA⁷:

with

and

We have also:

With and is the default variable⁸.

The derivative function regarding to x is equal to:

By developing the GA under, we find the following formula:

With

・ The GA formula under the Credit Risk+ model:

As we have seen to compute the GA formula, we need to calculate the following quantities, , and that depend to the model. The assumption of the

Credit Risk+⁹ model is that where. Then, we obtain the following relation:

We can explain the GA formula by computing the following components:

The expression of is given by¹⁰:

And

We have for the conditional variance:

With

We conclude that:

Therefore, we have:

These results we lead us to the GA formulation found it by Gordy and Lutkebohmert (2007) ¹¹:

With,

And

3. The Granularity Adjustment Approximation

The aim of this study is the implementation of algorithmic tests to test approximations of GA. These algorithmic tests will be established on R and under the following assumptions:

・ The HKI (Hannah-Kay Index) parameter is equal to 3.

・ The HIS (Hammami-Slime Index) parameter is equal to 0.25.

・ The generation of exposures follows the Log-normal distribution.

・ The parameter of the Gamma distribution is equal 0.31.

・ The quantile is equal to 99.9%.

3.1. The Reduced Form of GA

The authors of the GA formula below the Credit Risk+ suggest a simplification under the assumption that quantities of and are enough small. So, we can neglect and. The simplified GA becomes:

By the same way, we can approximate this formula below the Vasicek model giving the assumption and, by:

This test allows verifying the validity of these approximate formulas of GA. The Table 1 summarizes the formulations under the both models Vasicek and Credit Risk+.

The test implementation is based on portfolio generating of some exposures according to the Log-normal distribution. Then, we compute the full and the approximate GA under the both models Vasicek and Credit Risk+. We repeat this operation one thousand times to get 1000 portfolios at the end. Test steps are described on the following algorithm:

1) Generate 1000 exposures according to the Log-normal (10, 3) distribution.

2) Generate 1000 probabilities of default according to the uniform distribution.

3) Generate1000 correlation coefficient according to the uniform distribution between 0.12 and 0.24.

4) Compute the full GA according to the two models.

5) Compute the approximate GA according to the two models.

6) Iterate 1000 times the steps from 1 to 5.

7) Statistical test of the average under the generated data of the full and the approximate GA.

8) Statistical test of the variance homogeneity under the generated data of the full and the approximate GA.

This test allows us to determine the conditions of using the approximate GA in order to simplify computing. First, we get in the Vasicek model with an interval of default probabilities between 0 and 1%. We conclude that the two values are very close. Furthermore, the Student test of the average and the Fisher test of the variance are conclusive and we find respectively a p-value equal to 24% and 5.5%. This result underpins the approximate formula of the GA. On the other hand, if we have the un-conditional default probabilities go beyond of 1% then this approximation doesn’t more work. The Figure 1 reproduces the results of this test:

In regards to the Credit Risk+ model, we can prove using tests that the approximation formula of GA still suitable when the probabilities of default are between 0 and 10%. We get in by the same way and we generate the PDs between 0 and 10%. The Student test on the average and the Fisher test on the variance give respectively a p-value of 49% and de 16%. On the other side, this result is no more suitable for the PDs beyond of 10%. As conclusion, the condition that makes the approximation formula suitable for Vasicek model is the PDs portfolio between 0% and 1%, and for the Credit Risk+ model is the PDs portfolio between 0% and 10%. The Figure 2 shows the evolution of the full and the approximate GA.

3.2. The Regression of GA on the Concentration Indexes

・ The regression of the GA on the Herfindahl-Hirschman Index (HHI):

We find into the GA formula the square of shares, and these represent compo-

nents of the HHI¹² index. Furthermore, in the case of a homogeneous portfolio regarding to specific risk factors, we get a linear relation between the GA and the HHI:

where

The Figure 3 shows the evolution of the GA according to the HHI index in the case of homogenous portfolios ():

The goal of this test is to verify the validity of this relation on the non-homogeneous portfolio. For this, we establish the following test:

1) Generate 1000 exposures according to the Log-normal (10, 3) distribution.

2) Generate 1000 probabilities of default according to the uniform distribution (5%, 10%).

3) Generate 1000 correlation coefficient according to the uniform distribution between 0.12 and 0.24.

4) Compute the full GA according to the two models (Vasicek and Credit Risk+).

5) Compute the HHI index.

6) Iterate 1000 times the steps from 1 to 5.

7) Apply the linear regression under the simulated GA according to the simulated HHI.

If we take an interval of PDs between 0% and 20%, we obtain the following results in the Figure 4.

The Table 2 summarizes the characteristics of the linear regression.

From these results, we can deduce that the relationship of linearity between the GA and the HHI remains valid for minimum concentrations. Otherwise, you can have quite substantial dispersions around the regression for fairly major indexes.

・ The regression of the GA on the Hannah-Kay Index (HKI):

We couldn’t find directly the relation between the GA and the HKI even though in case of a homogeneous portfolio. Therefore, we will use an empirical approach to get this relation. The HKI¹³ is defined by:

Basing on the empirical experience, we get a non-linear regression relation:

We process in the same way to the last implementation. Indeed, we generate exposures with the Log-normal and we compute the GA and the HKI index. The description of the algorithm steps is:

1) Generate 1000 exposures according to the Log-normal (10, 3) distribution.

2) Generate 1000 probabilities of default according to the uniform distribution (5%, 10%).

3) Generate 1000 correlation coefficient according to the uniform distribution between 0.12 and 0.24.

4) Compute the full GA according to the two models (Vasicek and Credit Risk+).

5) Compute the HKI index.

6) Iterate 1000 times the steps from 1 to 5.

7) Apply the nonlinear regression under the simulated GA according to the simulated HKI.

In the case of homogenous portfolios, the Figure 5 shows the evolution of the GA according to the HKI index, and coefficients of the non-linear regression are respectively and (, ,):

If we take an interval of PDs between 0% and 20%, we obtain the following results in the Figure 6.

We can conclude that this relationship between the GA and the HKI remains valid for minimum concentrations. Otherwise, you can have quite substantial dispersions around the regression for fairly major indexes.

・ The regression of the GA on The Hammami-Slime Index (HSI):

We can’t directly find the relation between GA and HSI even though in case of a homogeneous portfolio. Therefore, we will use an empirical approach to get this relation. The HSI¹⁴ is defined by:

Using the empirical study, we get a non-linear regression relation:

We process in the same way to the last implementation. Indeed, we generate exposures with the Log-normal and we compute the GA and the HSI index. The description of the algorithm steps is:

1) Generate 1000 exposures according to the Log-normal (10, 3) distribution.

2) Generate 1000 probabilities of default according to the uniform distribution (5%, 10%).

3) Generate 1000 correlation coefficient according to the uniform distribution between 0.12 and 0.24.

4) Compute the full GA according to the two models (Vasicek and Credit Risk+).

5) Compute the HSI index.

6) Iterate 1000 times the steps from 1 to 5.

7) Apply the nonlinear regression under the simulated GA according to the simulated HSI.

In the case of homogenous portfolios, the Figure 7 shows the evolution of the GA according to the HSI index, and the coefficients of the non-linear regression are respectively and (, ,).

If we take an interval of PDs between 0% and 20%, we obtain the following results in the Figure 8.

We can conclude that this relationship between the GA and the HSI remains valid for minimum concentrations. Otherwise, you can have quite substantial dispersions around the regression for fairly major indexes.

4. Application: iBoxx Portfolio

In this section, we will apply the obtained results under an iBoox portfolio. We will build some portfolios given the composition of this index. We will deem that the portfolio building this index is the market portfolio. The iBoox contains 1663 exposures over 10 sectors and 36 countries. The total amount of debt is 1 trillion Euros. The Figure 9 and Figure 10 show repartitions by sector and by countries (the displayed data are dated 30/06/2015).

We can also have the repartition by rating in the Figure 11.

The Table 3 displays the mapping between the probabilities of default and the rating¹⁵.

Firstly, we can study the concentration of the iBoxx portfolio to get a global view of the concentration. The Lorenz curve, in the Figure 12, allows us to have the dispersion of exposures by counterparty.

Basing on the graph, we have an almost equal distribution between exposures. We can make a first feeling that the name concentration is small. Therefore, we use also the other metrics to confirm this conclusion. Indeed, we compute the tree concentration indexes and the GA. The Table 4 summarizes the result compute of these metrics.

Giving these results, we can conclude that the name concentration is neglected.

After this study, we will take a small portfolio with 100 exposures to see the impact of the number of exposures on the name concentration under these metrics. For this, we will do a random selection from the iBoxx composition. We can use regressions of the GA on concentration indexes to compute the name concentration risk. We use the same algorithms in the third section. The Figure 13 below shows the simulation result.

The Table 5 summarizes the obtained results:

There is a concentration risk rather important consideration at the GA, as it increases the costs in terms of provision approximately 21%. This result is consistent with the HSI index, unlike the HHI and HKI indexes.

5. Conclusion

This paper is dedicated, firstly, to model the name concentration under the Add-On approach; secondly, to approximate the GA using the concentration indexes. We established tests to find the relation between the GA and the indexes. These approximations allow us some simplification of the GA formula. As application, we chose the iBoxx composition as the credit portfolio.

These tests on the GA approximation enabled us to make the relation between the Ad-Hoc and the Add-On. We retained the regression between the GA and concentration indexes. Furthermore, the HSI index gave a more consistent measurement of portfolios with a small number of exposures.

However, these approximations can be used to simplify the GA calculation under the sector concentration. Indeed, the formulation of GA is more complex in the sector concentration than the name concentration.

Cite this paper

Slime, B. (2016). Credit Name Concentration Risk: Granularity Adjustment Approximation. Journal of Financial Risk Management, 5, 246-263. http://dx.doi.org/10.4236/jfrm.2016.54023

References

Annexes

・ The Vasicek model:

In 1987, Vasicek used the Merton model (1974) to modeling relations between the default events to get the assessment of the credit risk. We denote as the liability of the borrower i. The asset value of this borrower with a giving time t follows a geometric Brownian motion and verifies the following stochastic differential equation (SDE):

With are constant and is an Independent Brownian motion. represent the macroeconomic component (systematic risk) and is the specific factor (idiosyncratic risk). The Black & Scholes theory with a one year horizon gives us the solution of the SDE:

where are i.i.d (independent and identically distributed) and follow a Gaussian distribution.

The model supposes that default variables are Bernoulli:

Indeed, the default probability is equal to:

Therefore, the borrower is in default when:

If we set:

We get:

With and

The default condition becomes:

With

Then, we conclude that:

The Vasicek model use one systematic factor. The default probability of some borrower conditionally to this factor is equal to:

We can deduce that

Giving these results and under the assumption that borrowers loss are independent. The loss rate of the whole portfolio is:

We can obtain the expected loss conditionally to the systematic factor under the assumption that the loss giving default and the default event are independent:

We can use the Monte Carlo simulation on the systematic factor to compute this value.

・ The Credit Risk+ model:

The Credit Risk+ model was had developed by Credit Suisse Financial Products (CSFP). This model is the one of most used in the IRB Approach and he is one of reduced form models. The default rate is a stochastic variable and the default variable follows the Bernoulli distribution:

Credit Risk+ supposes that default probabilities are hazardous and systematic factors follow the Gamma distribution with the following function density:

, pour et

With and

In the case that the default frequency follows the Poisson distribution with as intensity, we get:

The default variable and the default frequency meet with the following relation. Therefore, the conditional probability is defined as:

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact jfrm@scirp.org

NOTES

¹See Annex.

²See Annex.

³See Wilde (2001) , Probing granularity, Risk Magazine, Vol 14, No 8, pp 103-106.

⁴See Gourieroux, Laurent, & Scaillet (2000) , Sensitivity analysis of Values at Risk, Journal of Empirical Finance.

⁵See Martin, & Wilde (2002) : Unsystematic credit risk, Risk Magazine 15(11), pp 123-128.

⁶See Vasicek (1987) . Probability of loss on loan portfolio, KMV Corporation, San Francisco, USA.

⁷See Annex.

⁸See Annex.

⁹See Credit Suisse Financial Products (1997) . Credit Risk+: A Credit Risk Management Framework. London, 1997.

¹⁰See Annex.

¹¹See Gordy, & Lutkebohmert (2007) , Granularity adjustment for Basel II, Discussion Paper Series 2: Banking and Financial Studies, Deutsche Bundesbank (1).

See Gordy, & Lutkebohmert (2013) , Granularity Adjustment for Regulatory Capital Assessment, International Journal of Central Banking.

See Lutkebohmert (2009) . Concentration Risk in Credit Portfolios. Springer.

¹²See Herfindahl (1950) . Concentration in the U.S. Steel Industry, Dissertation, Columbia University.

See Hirschmann (1964) . The paternity of an index. American Economic Review, 54, 5, pp. 761.

¹³See Hannah, & Kay (1977) . Concentration in modern industry. Mac Millan Press, London.

¹⁴See Slime, & Hammami (2016) . Concentration Risk: The Comparison of the Ad-Hoc Approach Indexes. Journal of Financial Risk Management, 5, 43-56.

¹⁵Moody’s Investor Service, 2010.