Received 5 January 2015; accepted 2 March 2015; published 5 March 2015

ABSTRACT

By this paper, we give an answer to the problem of definition of coherent risk measures on rearrangement invariant, solid subspaces of L⁰ with respect to some atom less probability space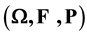. This problem was posed by F. Delbaen, while in this paper we proposed a solution via ideals of L⁰ and the class of the dominated variation distributions, as well.

Keywords:

Rearrangement Invariance, Dominated Variation, Moment-Index

1. Introduction

In (Delbaen, 2009) , the problem of defining a risk measure on a solid, rearrangement invariant subspace of 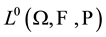-space of random variables with respect to some atomless probability space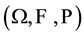. We recall that a vector space E, being a vector subspace of 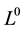is called rearrangement invariant if for random rariables 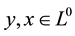, which have the same distribution, implies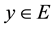. Also, the space E is solid if for andom viariables, , 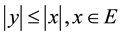implies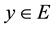. In (Delbaen, 2009) , there is an extensive treatment of this problem, related to the role of the spaces 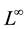and, compared to E, especially in (Delbaen, 2009) . On the other hand, the whole paper (Delbaen, 2002) is devoted to the difficulties of defining coherent risk measures on subspaces of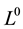, while it is proved that if the probability space is atomless, no coherent risk measure is defined all over 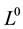(Delbaen, 2002) . Of course these attempts of moving from 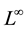to appropriately defined subspaces of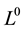, are related to the tail propertes of the random variables in actuarial science and finance and more specifically to heavy-tailed distributed random variables. The actual problem behind these seminal article by F. Delbaen is since we cannot define a coherent risk measure on the entire, whether subspaces of which are both alike and preserve nice distributional properties (from the aspect of heavy-tails). Especially, we treat the rearrangement invariance in the sense of remaining in the same class of distributions and not by requiring distributional invariance. This is the topic of our paper.

2. Ideals of L⁰ and Heavy-Tailed Distributions

It is well-known that since is a Riesz space, being ordered by the pointwise--a.e. partial ordering ³, it would be taken as a Riesz subspace of. Hence, it may be considered to be an order-complete Riesz space. Let us take an element y of, which corresponds to a heavy-tailed random variable. This indicates that either for for,

for any real number, where or. Heavy-tailed random variables may not have even a finite moment. On the other hand, according to (Aliprantis & Border, 1999) , the principal ideal generated by y in E, endowed by the norm

is an AM-space with order unit. We also have to mention the following relevant.

Lemma 2.1 If and y is a heavy-tailed random variable, then every is a heavy-tailed random variable.

Proof. Since, we get that for the sets, the inclusion holds, which implies for the corresponding cumulative distri- bution functions. Since for the integral

holds for any, this implies

for any.

We recall the class of dominated variation distributions:

This class is a sub-class of heavy -tailed distributions, see (Cai & Tang, 2004) .

Theorem 2.2 If, where denotes the class of dominated variation distributions respectively, then for every,.

Proof. According to what is proved in (Cai & Tang, 2004) , the class is convolution-closed, namely if, then. First, we have to prove that if, then, for any. Since

, there exists some such that. But. This is easy to prove, since if

for any, then in order to prove that

for any, then we get that the above limsup is equal to

for any. Hence,. Moreover, we have to prove that if, then. From the previous Lemma,

From the properties of the tail function of z we also have that since for, then

Hence,

Since,

which is the desired conclusion.

Hence we obtain subspaces E of, which are actually the ideals which satisfy the rearrangement invariance property, while they contain non-integrable distributions, in the sense that for any there is a maximum p for which the moment exists in. Let us discuss more this question. A notion which is very important is the one of the moment index. We recall that the moment index for a non-negative random variable x is equal to

We also recall that if, then, see in (Seneta, 1976) , (Tang & Tsitsiashvili, 2003) . The use of the moment index in the specific case is that despite the validity of the (Delbaen, 2002) , due to the fact that the elements of distributions lie in the class, we assure that at least in the ideal, we assure a general level of non-integrability of, given by a finite. About the question whether the class is the greatest in which the specific Theorem holds, we have to mention that if we move up to the class of the subexponential distributions, it is not convolution-closed, see for example in (Leslie, 1989) . As it is also well- known from (Aliprantis & Border, 1999) , the dual space of is an AL-space, since the ideal is an AM-space with unit, as mentioned above. Hence, we keep the dual pair

for any of the y described above.

3. Expected-Shortfall on Ideals of L⁰

Taking any whose, and defining the corresponding dual pair

we may define an Expected Shortfall-form risk measure on. We have to notice that satisfies both the order and the distributional rearrangement property, as a subspace of. This is due to the properties of the class of the dominated variation distributions. Hence we use (Kaina & Rüschendorf, 2009) of the dual (robust) representation of the usual Expected Shortfall in order to prove the following.

Theorem 3.1 The functional, where

is an -coherent risk measure, where is such that.

Proof.

1)

for any, due to the order completeness of the ideal (y-Translation Invariance).

2)

for any (Subadditivity).

3)

for any and (Positive Homogeneity).

4) If then for any we get. Hence by taking suprema all over , we ger (-Monotonicity).

Finally, if we suppose that the dual pair is a symmentric Riesz pair, or else that has order-

continuous norm (see also (Aliprantis & Border, 1999) ), then the values of R are finite since they represent the supremum value of a weak-star continuous linear functional on a weak-star compact set, which is the box of

functionals. Otherwise, the infinity of the values of R may be excused by the presence of heavy-tailed distributions.

References