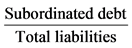Received 3 July 2014; revised 7 August 2014; accepted 25 August 2014

ABSTRACT

Using US commercial bank data over the period 2000 to 2008, we examine how the issuance of subordinated debt (SND) affects bank risk-taking and stability, efficiency, and deposit and loan growth rates. We identify the channels by which these effects occur and, using fixed- and random- effects models and system-GMM estimations, we provide evidence that supports these channels. As SND as a percentage of total liabilities rises, bank risk-taking falls. SNDs not only improve banks’ market discipline by directly reducing non-performing loans, but by leading to reduced overhead costs, and SNDs also boost banks’ efficiency and stability. Our results are robust under different model specifications and estimation methodologies.

Keywords:

Subordinated Debt, Market Discipline, Banking-Sector’s Efficiency, Stability, Non-Performing Loans, US Commercial Banks

1. Introduction

Market discipline, as it relates to the banking sector and subordinated debt (SND), it can be classified into two distinct processes: “market monitoring”, which refers to investors reacting to any change in a bank’s risk profile by incorporating those assessments into how they price SNDs; and “market influence”, which refers to bank managers responding to a security price change, by, for example, counteracting any adverse change in their firm’s condition¹. In the third pillar of Basel II, the Basel Committee on Banking Supervision (2001) required several disclosures―bank’s capital-risk exposure, risk assessment processes, and its capital adequacy ratio― that were aimed at encouraging market discipline and making it easier to monitor banks. The most important feature of these disclosures related to the extent to which private investors could observe and price the risks taken by banks, as these ultimately affect the banks’ management decisions. Studies that focus on market monitoring investigate the risk-sensitivity of the SND spread; however, little is known about the ability of SND investors to influence bank managers’ risk-taking decisions². This gap in the literature is what we address in this paper.

Although other researchers have examined how SNDs affect the cost efficiency of commercial banks³, we identify the channels by which SNDs affect not only the efficiency, but also the stability and growth of the banking system and find strong empirical support for the efficiency and stability channels. We show clearly that it is not just the price (spread) on SNDs that matters for market discipline―the amount of SNDs that banks hold is also very important.

How SNDs are priced is clearly important to their market discipline effects. For example, Blum (2002) argued that after pricing their SND contracts, banks could choose a higher level of risk than that before the contract, but, in repeated and ongoing relationships between investors and such banks, SND holders―after experiencing banks’ excessive risk taking―may require higher interest rates, thus disciplining these banks’ behavior. Thus, whenever SND holders are compensated with such a “risk premium”, they would become indifferent to the level of risk undertaken by banks.

However, the amount of SNDs also matters: if market discipline works then banks with larger amounts of SNDs, by decreasing their risk, may attract larger amounts of loans and deposits⁴. For these reasons, SNDs may not only improve banking stability by decreasing non-performing loans (NPLs), but they may also boost the efficiency and growth of the banking sector. In addition, banks with small SND balances have little incentive to respond to any change in the SND price because the burden of increased interest expense is not significant, even assuming that the SND is priced correctly and reflects the true risk level of the bank. Thus, when issuing SNDs the source of discipline originates not only from the higher price that the bank would face if it takes on a higher level of risk, but also from the higher interest expense when the bank has a substantial SND balance.

By directly investigating how changes in the price and amount of SNDs affect a bank’s risk characteristics, we are able to illustrate clearly the “practical side” of market discipline―the way in which market discipline actually works. Assuming that market monitoring is occurring, we find evidence of the impact of SNDs on market influence; that is, we examine how changes in SNDs may cause bank managers to react, counteracting any adverse changes in their bank’s condition (e.g., its non-performing loans).

This paper contributes to the literature on the market-discipline effects of SNDs in the banking industry in two ways. First, we comprehensively analyze the influence of SNDs on the incentives of bank management to reduce risk-taking activities. Although Krishnan et al. (2005) reviewed the “preventative influence” of SNDs by showing the average change in risk characteristics (that is, non-performing loans and leverage following the first SND issue), they did not find meaningful evidence of such influence. By using relevant control variables and more elaborate empirical models, our results prove that this “influencing phase” does indeed exist. Thus, with the help of some earlier work on the “monitoring phase”, we are able to link SNDs’ market-discipline effect to bank stability. Second, whereas previous studies of SNDs focused on the risk-taking behavior of banks, here we examine the issues of the stability, efficiency, and growth of the banking industry comprehensively using US commercial bank data. Using fixed- and random-effects models, we find strong empirical evidence that increases in the SND ratio not only decrease non-performing loans, but also decrease overhead costs (and net interest margins). This paper is organized as follows: Section 2 reviews the relevant literature; Section 3 provides empirical evidence of our hypotheses using fixed-and random-effects panel regressions; Section 4 shows the robustness of our empirical findings using panel-causality tests; and Section 5 concludes.

2. Literature Review

Traditional tests of market discipline focused on the ability of market forces to identify and control risk-taking in banks (e.g., Hannan and Hanweck, 1988 ). Flannery (1998) reviewed studies on US banks, whereas Sironi (2003) provided evidence from the European banking industry. Most empirical studies that examined the link between SNDs and market discipline focused on market monitoring, as they tested for the risk-sensitivity of SNDs’ spreads (e.g., Sironi, 2001 ). In relation to our hypotheses, the literature can be classified into three distinctive groups. The first group of studies focuses on the causal links between market discipline and the stability of banks. Schrieves and Dahl (1992) provided four different channels of positive association between bank capital and risk, whereas Blum (1999) suggested that increasing bank regulatory capital standards might have the unintended effect of causing banks to engage in increasingly risky behavior. Aggarwal and Jacques (2001) provided evidence of a negative association between bank capital and bank risk. Although Gropp and Vesala (2004) showed that SNDs may act as market-based limits to the moral hazards and excessive risk-taking of banks, Nier and Baumann (2006) reported that stronger market discipline resulting from uninsured liabilities and disclosures resulted in larger capital buffers.

The second group of studies focuses on the impact of market discipline on the efficiency of banks. Covitz et al. (2004) showed that SNDs are a relatively inexpensive substitute for equity capital and the tax code permits banks to deduct interest payments on debt instruments, but not on dividend payments on equity. Flannery (2005) showed that a security that reduced the deadweight cost of financial distress could permit banks to operate with more debt and hence a lower cost of capital. SNDs might also indirectly improve the efficiency of the banking system by decreasing NPLs and increasing equity. While some studies⁵ focused on bank risk and its impact on bank efficiency, other studies focused on bank capital and its impact on bank efficiency⁶. Berger and Mester (1997) claimed that, if there is a trade-off between risk and return, riskier banks might be more profit-efficient. Similarly, Maudos et al. (2002) showed that banks with higher risk induce a higher level of profit efficiency, but a lower level of cost efficiency. However, Park and Peristiani (1998) showed that risky thrifts offered higher interest rates, but attracted a smaller amount of uninsured deposits. In a similar vein, Martinez-Peria and Schmukler (2001) found that depositors disciplined banks by withdrawing deposits and by requiring higher interest rates as seen in Mexico during the Mexican Peso crisis. Finally, Fiordelisi et al. (2011) found that lower bank efficiency Granger-caused higher bank risk and increased bank capital preceding cost-efficiency improvements. For the relationship between bank capital and bank efficiency, Baer and Brewer (1992) observed that larger banks paid lower interest rates because they have a higher market-to-asset ratio. Similarly, Saunders and Schmacher (2000) showed that banks seek to lower the cost of holding relatively high capital ratios by demanding higher net interest margins (NIMs). However, Demirguc-Kunt and Huizinga (1999) showed that capital-to-lagged-asset ratio increased NIMs and Berger and De Young (1997) showed that decreases in cost efficiency are followed by increases in NPLs, and decreases in bank capital ratios generally preceded an increase in NPL for banks with low capital ratios.

The final group of studies investigated the impact of market discipline on the growth of banks. SNDs may indirectly boost the growth of loans and deposits by decreasing the risk profile of banks or improving their capital structure. Park and Peristiani (1998) showed that risky thrifts offered higher interest rates, but attracted smaller amounts of uninsured deposits. Demirguc-Kunt and Huizinga (2004) reported that higher capital ratios increased deposit growth, and Laderman (1994) found that a fall in capital-to-asset ratios below the regulatory minimum forced banks to decrease their outstanding loans. These and all previous studies will be used below to support our hypotheses regarding the expected effects of all the variables used in our “bank effect” regressions. These regressions allow us to ascertain how SND issuance affects banks’ stability, efficiency, and growth.

3. Fixed- and Random-Effects Models and Estimation Results

We use annual data for US commercial banks over the period 2000 to 2008 from the Federal Deposit Insurance Corporation (FDIC). We restricted banks in our sample to those with at least one share of SND during the sample period so that our final sample included 536 banks and 1619 bank-year observations. Table 1 presents variable definitions.

Table 2 presents the descriptive statistics for our variables. We can see that the mean of the SND ratio (sub-

ordinated debt divided by total liabilities) is 1.84%; this ratio increased until 2003, but decreased thereafter. Because of the US subprime mortgage crisis, the SND ratio recorded its lowest value, 1.42%, and the NPL ratio reached its highest value, 2.74%, during 2008. Bank efficiency, measured by the overhead-cost ratio was improving (decreasing) before the subprime mortgage crisis. The average capital-to-asset ratio over the sample pe-

riod is 9.46%. In addition, the growth rate of deposits and loans were highest during 2005, reaching 14.7% and 14.1%, respectively.

We use fixed- and random-effect models to examine the effect of increased SNDs on Bank Effect―variables presented below that are used to capture a bank’s stability, efficiency, and growth. Because the monitoring and influence phases may take time to be effective on Bank Effect, a one-year lagged SND ratio is used in the model shown in Equation 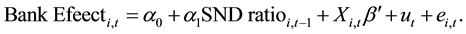(1):

(1)

where for bank at time 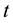is 1) stability, as measured by the NPL ratio in Table 4 and the Capital ratio in Table 5; 2) efficiency, as measured by the Overhead-cost ratio in Table 6 and Net interest margins in Table 7; and 3) growth, as measured by Deposit-growth rates in Table 8 and Loan-growth rates in Table 9; is the year-end balance of SND over total liabilities; includes bank-specific control variables; 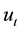is a time-specific effect to capture macroeconomic factors not observed in the other regressors; and 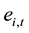is the error term, which is assumed to be independently and normally distributed.

Before performing panel estimations, we tested the stationarity of our data using the IPS panel unit test (Im et al., 2003) and modified inverse chi-square test of Choi (2003). For both tests, the panel unit test specified each ADF regression across the bank:

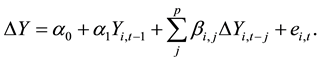(2)

where 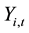is the bank characteristic variable for bank at time; 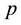is lag length in the ADF regressions; and the error terms, , are assumed to be independently and normally distributed random variables for all’s and’s. Table 3 presents the “-bar” test statistic under the null hypothesis that all panels have a unit root. We can see that we can reject the null hypotheses of nonstationarity for all, variables except securities and time deposits, at the 1% significance level. However, since we used the growth rates of securities and time deposits, we can apply traditional panel regression analysis to our data.

Our hypotheses regarding the effects of increased SNDs on bank stability, efficiency, and growth and associated regressions are presented in Sections 3.1 - 3.3 and Tables 4-9, respectively. Because the NPL and capital ratios may be endogenous variables in all these regressions, we first estimate the NPL ratio (capital ratio) without the and capital ratio (NPL ratio) and then extract the fitted values of the NPL ratio (capital ratio), which have now been purified from the impact of the ⁷. We use the fitted values of the NPL ratio (capital ratio) in the regressions reported in all of these tables. Also, because we cannot reject the random-effect model based on the Hausman test, estimation results for both fixed- and random-effects models are presented in all of these Tables.

3.1. SNDs and Bank Stability

Since a change in SNDs may lead bank managers to counteract adverse changes in bank conditions, we investigate the impact of an increase in SNDs on a bank’s risk profile and equity capital; specifically, we estimate the impact of increased SNDs on NPL (Table 4) and Capital ratios (Table 5).

Hypothesis 1: Stability: Increased SNDs decrease the NPL (Table 4) and increase the capital ratio (Table 5).

Table 4 reports the panel regression results when the NPL ratio is used as a dependent variable. The one period-lagged value of the SND ratio has a negative sign and is significant at the 1% critical level, which implies that when SNDs are issued this year, next year’s NPL ratio will decrease. This finding is consistent with Gropp and Vesala (2004) , who claim that SNDs may act as a market-based limit to the moral hazard and excessive risk-taking of banks and thus SNDs may actually decrease the overall risk of banks. It thus confirms that SNDs are an effective tool for market discipline. In other words, by strengthening the sensitivity between bank risk-taking and the SND spread (monitoring phase), the bank thereby reduces its excessive risk-taking (influencing phase).

Turning to the coefficient on the return on assets (ROA) variable―because ROA serves as an ex post performance measure, the negative relationship between it and the NPL ratio is consistent with the expected bankruptcy-costs hypothesis of Berger (1995) , who discussed performance problems, e.g., that a high ROA would be

Notes: a. is the test statistic defined by Im et al. (2003) as follows: ; b. is defined by Choi (2001) as follows:; c. In both tests, we adopt a one-year lag for ADF regressions. The Null hypothesis is that all panels have na unit root. ^** and ^* represent the significance level of 1% and 5%, respectively.

associated with a low level of loans that are not paid back. A bank’s liquidity can be measured by its Cash ratio and because a bank with greater liquidity will have less risk, this coefficient is expected to be negative (see, e.g., Aggarwal and Jacques (2001) ). However, in Table 4, this liquidity variable has no significant effect on the NPL ratio. While there is mixed evidence in the literature about the relationship between the NPL and Capital ratios⁸, here we find a positive relationship. Shrieves and Dahl (1992) proposed a net positive association between risk and capital when the positive effects due to regulatory costs, the unintended effects of minimum capital standards, bankruptcy cost avoidance, and managerial risk aversion outweigh the negative effects due to deposit insurance subsidies.

To recognize market discipline by depositors⁹, we include the Deposit ratio in the equation, which is expected to have a negative association with NPL ratio, as it does here. As Berger et al. (2009) note, market power in the banking industry may lead banks to exhibit greater portfolio risk, which suggests a positive relationship between Market share and the NPL ratio, which is what we found in Table 4.

a. The table reports the panel regression results of bank stability (non-performing loans) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the panel regression results of bank stability (capital ratio) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the panel regression results of bank efficiency (overhead costs) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the panel regression results of bank efficiency (net interest margins) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the panel regression results of bank growth (deposit growth rate) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the panel regression results of bank growth (loan growth rate) and SND ratio. The time effect is introduced to account for macroeconomic factors for both fixed and random effect model. One-year lagged SND ratio is used in regressions to consider the time market discipline to be effective. Hausman test indicates that whether fixed and random effect model is preferred, with the null hypothesis of no systemic difference between the coefficients of fixed and random effect model. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

Table 5 reports the impact of the SND ratio on the Capital ratio when controlling for other bank characteristics¹⁰. Consistent with Nier and Baumann (2006) , who showed that uninsured funding (bank deposits and SND normalized by total liability) strengthens market discipline and is effective in providing incentives for banks to limit their risk of default (by holding capital buffers against adverse outcomes), the estimated coefficient of the SND ratio is positive and significant at the 1% critical level.

We expect that the Cash ratio, a proxy for bank liquidity, would be negatively related to the Capital ratio because, following Aggarwal and Jacques (2001) , banks with greater cash have less demand for capital, and this is what we find in the random-effects model. Aggarwal and Jacques (2001) also argue that asset quality, as measured in the Loan-loss provision ratio, is expected to be positively associated with bank capital because low asset quality in its loan portfolio causes management to raise capital to avoid bankruptcy. In Table 5, the Loan-loss provision ratio appears to have no significant effect on a bank’s Capital ratio.

Berger (1995) finds that, to the extent that managers are involved in bank ownership, it is less costly for a profitable bank (high ROA) to signal its goodness by improving capital structure than it is for an unprofitable bank. Nier and Baumann (2006) and Flannery and Rangan (2008) assert that stocking retained earnings is one means of accumulating bank capital, implying that only profitable banks can send signals to be perceived as “good” banks by improving their capital ratio (Berger, 1995) or banks accumulate their equity capital stock by retained earnings¹¹. Thus, ROA should be positively related with the Capital ratio; this is what we find in Table 5¹².

According to Fonseca and Gonzalez (2010) , depositors discipline bank management by requiring high interest on their deposits; thus, a bank with high deposit costs will be willing to raise its capital base. Hence, the expected sign of the relationship between the Cost of deposits and the Capital ratio is positive, which is what we find in Table 5¹³. Prior studies yielded mixed evidence on the relationship between bank portfolio risk and capital structure. Shrieves and Dahl (1992) argue that whether this relationship is positive or negative depends on the relative forces of changing asset risk and leverage¹⁴. In Table 5, the NPL ratio, our proxy for bank risk has, ceteris paribus, no significant effect on the Capital ratio, implying that the Shrieves-Dahl positive factors offset the negative ones.

3.2. SNDs and Bank Efficiency

Here we investigate the direct and indirect impacts of new SNDs on the cost efficiency of banks, especially overhead costs (Table 6) and net interest margins (Table 7).

Hypothesis II: Efficiency: SNDs may boost the cost efficiency (Table 6) and deteriorate the profit efficiency (Table 7) of banks.

There are several ways in which SNDs may directly boost the cost efficiency of banks: by increasing their tax deductions for interest payments on debt (Covitz et al., 1997); and by lowering the cost of capital by reducing the deadweight costs of financial distress, permitting the bank to operate with more debt (Flannery, 2005) . SNDs may also indirectly affect the cost or profit efficiency of banks by changing their level of risky portfolios and capital. Berger and DeYoung (1997) showed that high levels of NPLs Granger-cause reductions in measured cost efficiency¹⁵. As discussed in Section 3.1, SNDs may decrease NPLs, which in turn may lower overhead costs and increase the net interest margins¹⁶. SNDs may also increase the capital ratio, which may also reduce overhead costs (Fiordelisi et al., 2011) or decrease the net interest margin¹⁷. Finally, SNDs may mean banks can pay lower interest rates on uninsured deposits, thereby increasing their net interest margins (Park and Peristiani, 1998) .

Table 6 presents the regression results for the Overhead-cost ratio. When both the NPL and Capital ratios are included in the regression, we find a negative and significant coefficient for the SND ratio, implying that the SND ratio decreases the overhead cost directly. While the capital ratio may boost the overhead cost (Altunbas et al., 2007) , an increased capital ratio decreases asset risk and this, in turn, may reduce overhead cost (Berger and Mester, 1997; Maudos et al., 2002) .

The Cash ratio is included to account for the opportunity cost of holding non-interest-bearing assets. Following Demirguc-Kunt et al. (1998) and Claessens et al. (2001) , we expect a positive sign on the Cash ratio, which is what we find, implying that a bank has high opportunity costs when it retains cash that earns no interest¹⁸. Micco et al. (2007) use the Non-interest income ratio to differentiate retail from wholesale banks; its coefficient is positive and significant, which is consistent with the view that non-interest income (e.g., commissions) tends to be higher for retail banks, which are relatively less efficient. Following Berger and Mester (1997) and Micco et al. (2007) , Market share is expected to be negatively related to the overhead-cost ratio because market power helps banks manage costs. In Table 6, however, Market share is insignificant.

The NPL ratio is also included as a proxy for asset risk as bad risk management is associated with bad operations management, including high overhead costs¹⁹. As expected, it has a positive and significant effect on the Overhead-cost ratio, ceteris paribus. There are two possible conflicting mechanisms to explain the effect of bank capital, Capital ratio, on its operational efficiency: Fiordelisi et al. (2011) argued that moral-hazard incentives may spur cost-cutting for banks with a sufficient capital base, whereas Altunbas et al. (2007) found that inefficient banks appear to retain high capital-to-asset ratios. Our results support Altunbas et al.’s view as the Capital ratio coefficient is positive and significant. Finally, to recognize the importance of economies of scale, Asset size is also included (Micco et al., 2007) ; as expected, its coefficient is negative and significant.

Table 7 shows the regression results with the Net interest margin as the dependent variable; these estimation results are quite similar to those for the Overhead-cost ratio regressions in Table 6. Because bank management may try to raise its margin to compensate for high asset risk, we include the NPL ratio (Angbazo, 1997; Carbo- Valverde and Rodriguez 2007) , expecting its effect, ceteris paribus, to be positive; its effect however is not significant here. As discussed in Section 3.2, SNDs may either increase or decrease net interest margins. Here, the coefficient on the SND ratio is negative and significant at the 1% critical level, implying that an increased SND ratio decreases Net interest margins so that SNDs promote the efficiency of the banking system.

The Cash ratio is included as, following Angbazo (1997) , it represents the opportunity cost of holding non-interest-bearing assets or liquidity risk. Thus, the expected sign of the relationship depends upon the relative size of two competing effects: holding such assets requires a bank to raise margins to cover its profit, but also reduces the liquidity risk of the bank, which then lowers margins. In Table 7 the Cash ratio is insignificant, indicating that these two competing effects may have cancelled each other out. The Overhead-cost ratio is included as a proxy for cost efficiency because, according to Demirguc-Kunt and Huizinga (1999) and Claessens et al. (2001) , bank management may be willing to compensate for high overhead costs by raising its net interest margin, so its expected effect is positive. This positive and significant coefficient implies, as expected, that banks pass on some of their overhead costs to their depositors and lenders.

Following Carbo-Valverde and Rodriguez (2007) , we include the Non-interest-income ratio in order to account for a potential cross-subsidization strategy²⁰. This ratio has significant negative effect, implying that a cross-subsidization strategy (in which a bank diversifies its income to non-traditional sources, such as commissions and trading income) results in a lower margin in its traditional products, deposits and loans²¹. Because holding excessive capital is costly to the bank and may induce it to raise margins to cover its costs, some researchers²² claim that the Capital ratio may be positively associated with Net interest margins. Thus, we expect―and find―a significant positive association between the Capital ratio and the Net interest margin.

3.3. SNDs and Bank Growth

We focus here on the impact of SNDs on deposit- and loan-growth rates; estimation results are shown in Table 8 and Table 9, respectively. If market discipline works then banks with larger amounts of SNDs―by reducing their risk―may attract larger amounts of insured and uninsured deposits, leading to higher growth rates in their deposits and loans²³.

Hypothesis III: Growth: New SNDs may indirectly boost the deposit (Table 8) and loan (Table 9) growth rates of banks by decreasing risk and increasing equity ratios.

In the deposit-growth-rate equation in Table 8, the coefficient of the lagged SND ratio is positive and significant, implying that a bank with a higher SND ratio can attract more deposits because depositors prefer lower-risk banks. This finding is consistent with Park and Peristiani (1998), Martinez-Peria and Schmukler (2001) , and Demirguc-Kunt and Huizinga (2004) .

Both Market share and Asset size are included because depositors prefer banks with high market power or larger asset size (Park and Peristiani, 1998) . Market share is positive and significant, indicating that banks with market power readily attract deposits; however, Asset size is not significant. Following Martinez-Peria and Schmukler (2001) and Demirguc-Kunt and Huizinga (2004) , the Overhead-cost ratio is included. If overhead costs rise due to the provision of higher-quality banking services, depositors would choose that bank to deposit their money in, yielding a positive coefficient, which is what we find here.

Because a bank paying higher interest can attract more deposits, the Cost of deposits is included here (Demirguc-Kunt and Huizinga, 2004) ; however, its effect is not significant. Both the NPL and Capital ratios are included as proxies for both asset and leverage risk²⁴. The estimated coefficient for the NPL ratio is negative and significant, which is consistent with Martinez-Peria and Schmukler (2001) ; that is, depositors disciplined banks by withdrawing deposits during the financial crisis. However, the estimated coefficient for the Capital ratio is positive and significant, implying that depositors prefer to put their money in a bank that has enough capital to be solvent in the case of a financial crisis²⁵.

Table 9 shows the regression results of the loan-growth-rate model with the SND ratio as a key exogenous variable. The estimated coefficient of the SND ratio is positive and significant at the 5% critical level only when a limited number of exogenous variables are included, but it is insignificant when the full set of independent variables is used. Consequently, we could not find robust evidence that increases in the SND ratio significantly boosts loan growth. Perhaps this result is due to the fact that with additional SNDs, banks with low initial capital may ultimately reduce loans to increase their risk-adjusted capital ratio (Baer and McElravey, 1992) , thus offsetting our hypothesized loan growth effect.

The growth rates of both time deposits and securities are included to represent the funding effect, and both are expected to have positive signs, as they do²⁶. Following Berger and Udell (2004) , we also include Market share to account for market power. As in prior studies, the Capital ratio is included to recognize both bank-lending and bank-capital channels. Both Market share and bank capital, the Capital ratio, are expected to have positive signs as an increase in either would help the bank expand its lending capacity; however, only the Capital ratio has a significant coefficient in this table.

4. Panel-Causality Tests

Even though fixed- and random-effects models yield simple and clear relationships between the issuance of SND and bank characteristics, the results we have obtained so far do not indicate any causal relationships. To examine causality, the model should involve lagged dependent and independent variables, which is not possible in the standard regression model. Holtz-Eakin et al. (1988) developed a dynamic panel model to address the causality problem and Arellano and Bond (1991) proposed the “difference” generalized method of moments (GMM) to estimate this model. The difference GMM estimators are designed for a dynamic panel model that has a relatively short time span and many individuals, allowing for idiosyncratic disturbance with heteroscedasticity and autocorrelation in individuals, and some regressors are not strictly exogenous. Arellano and Bond (1991) use a first-difference equation to eliminate individual-specific effects and then estimate a first-difference with a lagged level as the instrument in the following moment conditions:

For and

For and

For and

where Bank Effect is any one of the bank stability, efficiency, or growth variables discussed above; and the SND ratio and, the vector for the key control variables, are weakly exogenous variables. However, Blundell and Bond (1998) demonstrated that, in the case of persistent explanatory variables, the first-differenced estimator may suffer from the problem of weak instruments. Following Arellano and Bover (1995) , they develop a “system”-GMM with additional moment conditions that differentiates between regressors as instruments uncorrelated with individual fixed effects to estimate level equations by the following level moment conditions:

for

for

for

With these additional moment conditions, the system-GMM is more efficient than the difference-GMM. Taking all moment conditions together, we estimate our panel’s Granger-causality test using the system-GMM estimators in the following equations²⁷:

(3)

Tables 10-12 show the estimation results of the system-GMM estimators for the bank stability, efficiency,

a. The table reports the Granger-causality test for SND ratio to bank stability, using system-GMM estimators (Arellano and Bover, 1995; Blundell and Bond, 1998) . The Hansen test is used to verify over-identifying restrictions, with the null hypothesis of orthogonality between instrumental variables and residuals. The serial correlation test is the Arellano-Bond test that null hypothesis is differenced errors exhibit no second-order serial correlation. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the Granger causality test for SND ratio to bank efficiency, using system-GMM estimators (Arellano and Bover, 1995; Blundell and Bond, 1998) . The Hansen test is used to verify over-identifying restrictions, with null hypothesis of orthogonality between instrumental variables and residuals. The serial correlation test is the Arellano-Bond test that null hypothesis is differenced errors exhibit no second-order serial correlation. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

a. The table reports the Granger-causality test for SND ratio to bank growth, using system-GMM estimators (Arellano and Bover, 1995; Blundell and Bond, 1998) . The Hansen test is used to verify over-identifying restrictions, with null hypothesis of orthogonality between instrumental variables and residuals. The serial correlation test is the Arellano-Bond test that null hypothesis is differenced errors exhibit no second-order serial correlation. t-statistics are in parentheses. ^** and ^* represent the significance level of 1% and 5%, respectively.

and growth variables. To test the validity of the instruments, we use Hansen’s test of over-identifying restrictions, and we cannot reject the null hypothesis that the instrumental variables in the model are not correlated with residuals. We also report on the Arellano-Bond (AB) test for autocorrelation of order 2. We cannot reject the null hypothesis of second-order autocorrelations in any of the models presented in Tables 10-12.

Table 10 presents the results for the system-GMM estimation, where the dependent variables are the NPL ratio (column 1) and the capital ratio (column 2). The one-year-lagged SND ratio is negative and significant for the NPL ratio, but positive and significant for the capital ratio, suggesting that an increase in the SND ratio Granger-causes a reduction in the asset portfolio risk (NPL ratio) and an increase or improvement in the capital ratio in the following year. Consistent with the results from our fixed- and random-effects models, these panel- causality tests confirm the market-influencing effect of SNDs on bank risk.

The first column in Table 11 shows that an increased SND ratio has a negative impact on the bank’s overhead-cost ratio. As expected from the fixed- and random-effects models, the increased SND ratio Granger- causes a reduction in banks’ overhead costs. Furthermore, the second column of Table 11 shows that an increased SND ratio Granger-causes a decrease in net interest margins, which is consistent with our fixed- and random-effects model results in Table 7.

Table 12 shows the system-GMM estimation results for the effect of the SND ratio on deposit and loan growth rates. First, it is shown that a one-year lagged SND ratio does not Granger-cause the growth rate of deposits (first column), nor does it Granger-cause the growth rate of loans (second column). In other words, we could not find evidence that a one-year-lagged SND ratio boosts the growth rate of either bank deposits or loans. Thus, the positive relationship between the lagged SND ratio and deposit growth rates found in Table 8 may not be because issuing SNDs causes growth, but rather because only banks with deposit growth potential are able to issue large SNDs. Thus, an indirect mechanism of SNDs on bank growth is not evident from our empirical results, even though a reduction in a bank’s risk level, which may be induced by its issuing SNDs, is helpful to its growth.

5. Conclusion

While previous studies of SNDs focused on the “monitoring phase” of market discipline and investigated the risk-sensitivity of SND spread, our study has focused on the “influencing phase” of market discipline. We have directly tested the impact of an increased SND ratio on a bank’s risk (measured by nonperforming loans and capital ratio), efficiency (measured by overhead cost and net interest margin), and the growth rates of deposits and loans of US commercial banks over the period 2000-2008. Using both fixed- and random-effects models as well as panel-causality tests, we have found that increased SND ratios in US commercial banks have: decreased the next period’s non-performing loans and increased the next period’s capital ratio; and decreased the next period’s overhead cost and net interest margins. We could not, however, find robust evidence that increases in the SND ratio have a significant impact on bank growth (that is, its deposit- and loan-growth rates). Our empirical results thus extend the importance of SNDs from their impact on bank stability to the area of banking-sector efficiency.

Given how difficult it is to ensure that banks behave appropriately, our findings provide a rationale for regulatory authorities to make greater use of SND regulation, as SND issuance has both direct and indirect positive effects on bank behavior. Capital requirements are not enough to ensure prudent bank behavior; however, capital requirements together with SND regulation may be an effective way for authorities to discipline banks (Chen and Hasan, 2011) .

Cite this paper

Sang-OokShin,Hong-GhiMin,Judith A.McDonald, (2014) The Market-Discipline Effects of Subordinated Debt: Enhanced US Commercial Banking-Sector Efficiency and Stability. Journal of Financial Risk Management,03,78-95. doi: 10.4236/jfrm.2014.33009

References

NOTES

^*Corresponding author.

¹See Bliss and Flannery (2002) .

²See Flannery (1998) and Sironi (2001) .

³E.g., Raviv and Hilscher (2011) examine how SNDs impact banks’ deposit insurance premiums; Covitz et al. (1997) examine how SNDs affect tax deductions on interest payment on debts; Flannery (2005) examines their impact on the cost of capital; and Park and Perisitani (1998) examine their effect on interest payments on deposits.

⁴See Park and Peristiani (1998) , and Martinez-Peria and Schmukler (2001) . With additional SNDs, banks with low initial capital may try to reduce loans to increase their risk-adjusted capital ratio (Baer and McElravey, 1992) .

⁵See Berger and Mester (1997) , Maudos et al. (2002) , and Fiordelisi et al. (2011) .

⁶See Demirguc-Kunt and Huizinga (1999) , Saunders and Schmacher (2000) , and Berger and De Young (1997) .

⁷See Shrieves and Dahl (1992), Jacques and Nigro (1997) , and Aggarwal and Jacques (2001) .

⁸ Shrieves and Dahl (1992) and Aggarwal and Jacques (2001) .

⁹ Park and Peristiani (1998) and Martinez-Peria and Schmukler (2001) .

¹⁰SNDs are partly substitutable with equity capital to meet minimum capital requirements set by the Basel Committee on Banking Supervision (2001) . However, Raviv (2004) and Flannery (2005) noted that SNDs would increase the level of leverage and the probability of failure so that SNDs and capital ratios could have a negative relationship. If the market-discipline effect of SND on holding capital buffers exceeds the leverage effect, increased SNDs could increase the capital ratio. Because the current version of the Basel Accords explicitly requires that banks keep a certain (Tier 1) as well as a total (combined Tiers 1 and 2) capital ratio, SNDs may no longer be a good substitute for bank capital.

¹¹ Nier and Baumann (2006) and Flannery and Rangan (2008) .

¹²ROE may be another alternative for bank profitability. Because ROE is the product of ROA and the inverse of the capital ratio (i.e., Total Assets/Capital), ROE and the capital ratio are negatively related for a given ROA (Athanasoglou et al., 2008) . Thus, we used ROA rather than ROE as a proxy for bank profitability. The regression results that used ROE rather than ROA (not reported) showed little change in both the NPL- and capital-ratio models.

¹³Cost of deposits is measured as the average interest expense paid on bank time deposits.

¹⁴These factors are listed earlier in this section.

¹⁵ Maudos et al. (2002) and Berger and Mester (1997) .

¹⁶ Angbazo (1997) and Carbo-Valverde and Rodriguez (2007) .

¹⁷ Saunders and Schumacher (2000), Lepetit et al. (2008) , and Maudos and Solis (2009).

¹⁸ Demirguc-Kunt et al. (1998) and Claessens et al. (2001) .

¹⁹ Berger and Mester (1997) and Maudos et al. (2002) .

²⁰A bank whose operation is diversified from traditional interest income may charge lower margins.

²¹ Micco et al. (2007) and Carbo-Valverde and Rodriguez (2007) .

²² Saunders and Schumacher (2000) , Lepetit et al. (2008) , and Maudos and Solis (2009).

²³ Park and Peristiani (1998) and Martinez-Peria and Schmukler (2001) .

²⁴See Martinez-Peria and Schmukler (2001) and Demirguc-Kunt and Huizinga (2004) .

²⁵Ibid.

²⁶See Kishan and Opiela (2000, 2006) and Altunbas et al. (2002).

²⁷We use AIC and BIC for the choice of lag length of 1.