ABSTRACT

Sufficient conditions to guarantee the existence and global exponential stability of periodic solutions of a CohenGrossberg-type BAM neural network are established by suitable mathe matical transformation.

1. Introduction

Many important results on the existence and global exponential stability of equilibria of neural networks with time delays have been widely investigated and successfully applied to signal processing system. However, the research of neural networks involves not only the dynamic analysis of equilibrium point but also that of periodic oscillatory solution. In practice, the dynamic behavior of periodic oscillatory solution is very important in learning theory [1,2], which is motivated by the fact that learning usually requires repetition, some important results for periodic solutions of Hopfield neural networks or Cohen-Grossberg neural networks with delays have been obtained in Refs. [3-15].

The objective of this paper is to study the existence and global exponential stability of periodic solutios of a class of Cohen-Grossberg-type BAM neural networks (CGBAMNNs) with time-varying delays by suitable mathematical transformation.

The rest of this paper is organized as follows: preliminaries are given in Section 2. Sufficient conditions which guarantee the existence and global exponential stability of periodic solutions for the CGBAMNNs are established Section 3. An example is given in Section 4 to demonstrate the main results.

2. Preliminaries

Consider the following periodic CGNNs with timevarying delays (see Equation (1)):

For, and. denote the state variables of the ith neuron, denote the signal functions of the jth neuron at time t;  denote inputs of the ith neuron at time t; represent amplification functions; are appropriately behaved functions; and and are connection weights of the neural networks, respectively; 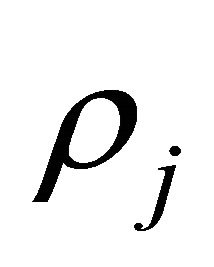are positive constants which correspond to the neuronal gains associated with the neuronal activations; correspond to the finite speed of the axonal signal transmission at time t and there exist constants such that, and are all continuously periodic functions on [0, +∞) with common period T > 0.

Throughout this paper, we assume for system (1) that

(H₁) Amplification functions are continuous and there exist constants such that for.

(H₂) are T-periodic about the first argument and there exist continuous T-periodic functions such that

.

(H₃) For activation functions, there exist positive constants such that

(1)

For any continuous function on,

and denote andrespectively.

For any

define

and for any

,

define

in which

.

Denote

is continuous on.

Then is a Banach space with respect to.

The initial conditions of system (1) are given by

(2)

where

.

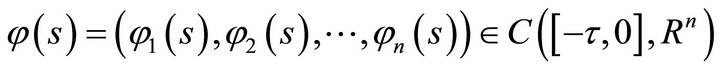Le denotes any solution of the system (1) with initial value.

Definition 1. An solution 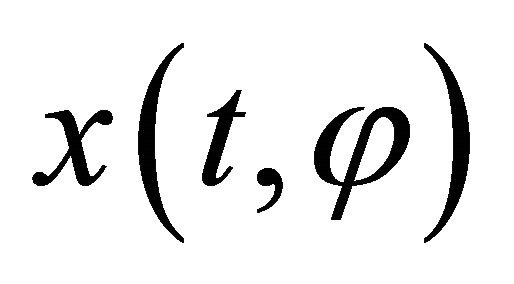of system (1) is said to be globally exponentially stable, for any solutions 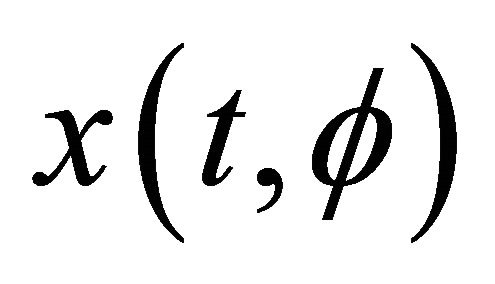of the system (1), if there exist positive constant and such that

(3)

Lemma 1. Under assumptions (H₁)-(H₃), system (1) has a T-periodic solution which is globally exponentially stable, if the following conditions hold.

(H₄) Assume that there exist constants such that,.

(H₅) is a nonsingular M-matrix, where

Proof. If, the model (2.1) in [14] reduces to the system (1), we know that Lemma 1 holds from Theorem 3.1 with r = 1 in [14].

3. Periodic Solutions of CGBAMNNs with Time Varying Delays

Consider the following CGBAMNNs with time-varying delays:

(4)

for, 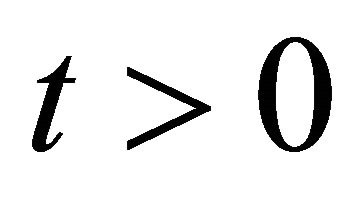and and denote the state variables, and denote the signal functions, and denote inputs; and represent amplification functions; and are appropriately behaved functions;, , and are the connection weights and, are positive constants, which correspond to the neuronal gains associated with the neuronal activations; Time delays and correspond to the finite speed of the axonal signal transmission at time t and there exist constants and such that,;, , , , , , and are all continuously periodic functions on with common period.

Throughout this paper, we assume for system (4) that

(H₆) Amplification functions and are continuous and there exist positive constants and such that, ,.

(H₇), are T-periodic about the first argument and there exist continuous T-periodic functions and such that

(H₈) For activation functions and, there exist constants and such that

The initial conditions of system (4) are given by

where

,

Theorem 1. Under assumptions (H₆)-(H₁₀), system (4) has a T-periodic solution which is globally exponentially stable, if the following condition holds.

(H₉) Assume that there exist constants  and such that and hold for.

(H₁₀) The followingis a nonsingular M-matrix, and

(5)

in which

Proof. Let

(6)

It follows that system (4) can be rewrote as

(7)

for.

Initial conditions are given by

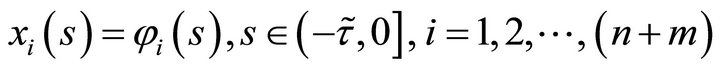(8)

Hence system (7) is a special case of system (1) in mathematical form in which there are n+m neurons and connection weights for and. Under conditions (H₆)-(H₁₀), from Lemma 1, we obtain that system (7) has a T-periodic solution which is globally exponentially stable, if the following matrix is a M-matrix, and

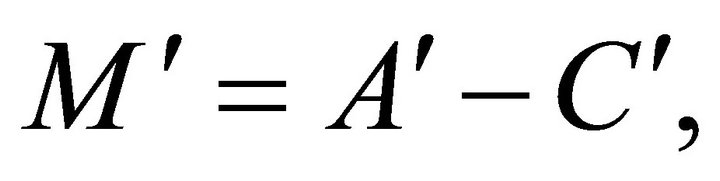(9)

where

in which

Then, we know from (6) and (9) that Theorem 1 holds.

4. An Example

Consider the following CGBAMNNs with time delays:

(10)

It is easy to verify system (10) satisfies (H₆)-(H₉). In addition, system (10) satisfies (H₁₀) because

is a nonsingular M-matrix. According to Theorem 1, system (10) has a 2-periodic solution which is globally exponentially stable. Figure 1 shows the dynamic behaveiors of system (10) with initial conditions (0.8, 0.9).

Remark 1 The results in [3,15] have more restrictions than the results in this paper because conditions for the results in [3,15] are relevant to amplification functions. In addition, in view of proof of Theorem 1, since CGBAMNNs with time-varying delays is a special case of CGNNs time-varying delays in form as BAM neural networks is a special case of Hopfield neural networks, many results of CGBAMNNs can be directly obtained from the ones of CGNNs, needing no repetitive discussions, which coincide with the conclusion in [16,17].

REFERENCES