American Journal of Climate Change
Vol.04 No.03(2015), Article ID:56390,13 pages
10.4236/ajcc.2015.43016
A Comparison of ANN and HSPF Models for Runoff Simulation in Balkhichai River Watershed, Iran
Farzbod Amirhossien1*, Faridhossieni Alireza2, Javan Kazem3, Sharifi Mohammadbagher1
1Department of Civil and Environmental Engineering, Ferdowsi University, Mashhad, Iran
2Department of Water Engineering, Ferdowsi University, Mashhad, Iran
3Department of Civil and Environmental Engineering, Tarbiat Modares University, Tehran, Iran
Email: *amir.farzbod@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2015; accepted 15 May 2015; published 18 May 2015
ABSTRACT
In this study, the capability of two different types of models including Hydrological Simulation Program-Fortran (HSPF) as a process-based model and ANN as a data-driven model in simulating runoff was evaluated. The considered area is the Balkhichai River watershed in northwest of Iran. HSPF is a semi-distributed deterministic, continuous and physically-based model that can simulate the hydrologic cycle, associated water quality and quantity and process on pervious and impervious land surfaces and streams. Artificial neural network (ANN) is probably the most successful learning machine technique with flexible mathematical structure which is capable of identifying complex non-linear relationships between input and output data without attempting to reach the understanding of the nature of the phenomena. Statistical approach depending on cross-, auto- and partial-autocorrelation of the observed data is used as a good alternative to the trial and error method in identifying model inputs. The performances of ANN and HSPF models in calibration and validation stages are compared with the observed runoff values in order to identify the best fit forecasting model based upon a number of selected performance criteria. Results of runoff simulation indicated that the simulated runoff by ANN was generally closer to the observed values than those predicted by HSPF.
Keywords:
HSPF Model, Artificial Neural Network (ANN), Runoff Simulation, Balkhichai River Watershed

1. Introduction
Streamflow is one of the most important processes in the hydrological cycle and its prediction is vital for water resources management and planning [1] . Computer simulation models of watershed hydrology and artificial intelligent techniques are widely used for runoff simulation and forecasting. The use of watershed models is increasing due to the growing demands of improving runoff quantity.
Over the last decades, artificial intelligent techniques have been introduced and widely applied in hydrological studies as powerful alternative modelling tools, such as Artificial Neural Network (ANN) [2] - [6] , and fuzzy inference system (FIS) [7] - [9] . In addition, Shamseldin [10] (1997), Kumar et al. [11] and Mutlu et al. [12] compared ANNs with different input variables for runoff simulation. The comparisons showed that the ANN models applying both with rainfall and discharge as input variables gave better results than the models with rainfall as the input. When the model utilizes of rainfall values as the input variables, the simulated hydrographs do not match the measured hydrographs so well [13] [14] . Although better fits between the simulated and measured hydrographs have been reported in other studies, where additional variables such as temperature [15] , evaporation [16] and, soil moisture [17] have been included as inputs for the ANN model.
HSPF is a semi-distributed, conceptual model that combines spatially distributed physical attributes into the hydrologic response units. In this model, surface runoff is simulated primarily as an infiltration-excess process. HSPF has been used for simulation of various hydrological conditions [18] [19] , non-point source pollutants including contaminated sediment [20] , and land use management and flood control scenarios [21] . Abdullah et al. have used of HSPF model for runoff simulation of a watershed in Jordan. The results showed that monthly calibration and verifications produced good fit with correlation coefficients equal to 0.928 and 0.923, respectively. Also, daily simulation results showed lower correlation coefficient of 0.785 [22] . Al-Abed and Whiteley applied HSPF model for runoff simulation in the Grand River watershed; located in Southern Ontario, Canada, with a drainage area of about 6965 km2 [23] . Their study revealed very satisfactory results in the calibration step and the percentage of error between the yearly simulated and the yearly observed yearly discharge values ranged between 4% to 16%.
Not only ANNs and HSPF have been widely used for runoff, pollution and sediment simulation, but also some researchers have been performed based on the comparison between mathematical models and ANNs [24] - [27] . Wang et al. have applied both HSPF and ANN models for runoff and pollution simulation of the eleven watersheds in north of Bremerton, WA. Results of both the ANN model and the HSPF model bore similar accuracy levels [28] . Considering the cost/product factor, this study shows that the ANN modeling approach provides a cost-effective alternative tool for predicting rainfall-runoff relationships. In this study, ANN and HSPF are evaluated for the simulation of Balkhichai River stream flow in Iran.
2. The Study Area
The study area is Balkhichai River watershed (Figure 1), located in the northwest of Iran, between 47˚50'E to 48˚18'E, and 37˚50'N to 38˚16'N. The Balkhichai River watershed area is about 1214 km2 that plays an important role on the region agriculture. Balkhichai River length is about 40 km and it is the most important river in the region. Watershed outlet is Ardebil station located in the northern part of the watershed. The region consists of mountainous areas in the west and northwest. The watershed elevation varies from 1280 m to 4732 m. Land use is mainly open grass (former pasture and hay fields), mountains, and the land use is agricultural, rural and urban residential. The mean annual precipitation in this watershed (stations are presented in Table 1) is very little in comparison with world average of 800 mm. The slope watershed is variable between 0 to 60 percent that the lowest (minimum) slope located in the center of watershed is between 0 to 2 percent. The satellite images are taken from of LAND SAT5 satellite in 2006 year. Figure 1 shows the location of 2 synoptic meteorological stations in the watershed and Table 1 shows the coordinates and the average of the observed temperature and precipitation values of these stations.
3. Methodology
3.1. Data
Temperature and precipitation are the two basic variables, which are measured at meteorological stations. The training input dataset includes a total of 2557 data records between 2004 and 2010. The testing input dataset
Figure 1. The study area.
Table 1. Properties of the synoptic stations.
consists of a total of 729 data records, which were observed during in the last 2 years (2011-2012). Hourly precipitation and temperature data were utilized as inputs to the HSPF model. Some data about of different land use classes in the Balkhichai watershed were retrieved during 3 days of field survey in the watershed. Then Land use classifications for the Balkhichai River were retrieved from the satellite image processing using the maximum likelihood classification.
3.2. HSPF Hydrological Model
In this study, Hydrological Simulation Program FORTRAN (HSPF) was used for simulation of Balkhichai River runoff. HSPF is a set of computer codes, which was developed by the US Environmental Protection Agency. It is based on the Stanford Watershed Model IV [29] . HSPF has been generated by the combination of Stanford Watershed Model IV with Agricultural Runoff Management Model (ARM) [30] , Non-point Source Runoff Model (NPS) [31] , and Hydrological Simulation Program (HSP) [32] - [34] . This model can simulate the hydrological processes over on permeable and impermeable land surfaces and streams [35] . It has been widely used in Asian and other parts of the world in the climate change studies [22] [36] .
HSPF is a semi-distributed deterministic, continuous and physically based model. The PERLND, IMPLND, and RCHRES modules are the three main modules of HSPF which help to simulate permeable land segments, impermeable land segments, and free-flow reaches, respectively. Detailed information about these modules can be found in the literatures [34] [38] [39] . Figure 2 exhibits the hydrological cycle processes in HSPF model. HSPF model uses a Storage Routing technique to route water in each stream-branch. Infiltration in permeable land is calculated based on Richards’ equation [34] . Actual evapotranspiration (ET) is calculated by Penman or Jensen formulas. Table 2 shows key HSPF parameters. These parameters should be calibrated during the calibration process. LZSN is the lower zone nominal capacity, which is the most important parameter in infiltration capacity. It is called in HSPF with the INFILT parameter. AGWRC is defined as the rate of today’s flow divided by the rate of yesterday’s flow, which is depended on topography, climate, soil properties and land use. UZSN is influenced by LZSN [35] . Other parameters that they have not presented in Table 2 are estimated using the
Figure 2. HSPF conceptual hydrological model [37] .
Table 2. The parameters of HSPF model in simulation process [40] .
BASINS (Better Assessment Science Integrating Point and Nonpoint Sources) software based on topographic, soil properties and land use data. Then the estimated parameters are introduced to HSPF. The BASINS is developed to promote better assessment and integration of point and nonpoint sources in watershed and water quality management. It integrates several environmental key data sets with improved analysis techniques. Several types of environmental programs can benefit from the use and application of such an integrated system in various stages of environmental management planning and decision making [34] . The data from 2004 to 2010 were utilized for HSPF model calibration and the data from 2011 to 2012 were used as validation datasets.
3.3. Artificial Neural Networks (ANN)
ANN inspired by using studies of biological neural system is composed of processing elements called neurons or nodes [41] . In literature, different types of ANN methods are used for forecasting and modeling the engineering Problems [12] . ANNs with one hidden layer are commonly used in hydrological modeling [42] since these networks are considered to provide enough complexity to simulate the nonlinear-properties of the hydrological process accurately.
A FFNN (Feed Forward Neural Network) consists of at least three layers of input, output and hidden layers. The input signals presented to the system in input layer are processed and forwarded into the hidden layer. The summation of the weighted input signals is transferred by a nonlinear activation function. The response of the network is compared with the actual observation results and the network error is calculated. The error of network is propagated backwards through the system and the weight coefficients are updated (Figure 3).
3.4. Evaluation Criteria
Table 3 shows the evaluation criteria that use in this study. The root-mean square error (RMSE) evaluates how closely predictions match observations. Values may range from 0 (perfect fit) to 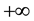 (no fit) based on the relative range of the data. The coefficient of determination, R, known as the square of the sample correlation coefficient, ranges from 0 to 1 and describes the amount of observed variance explained by the model. A value of 0 implies no correlation, while a value of 1 suggests that the model can explain all of the observed variance. The Nash-Sutcliffe coefficient of Efficiency, ENS, measures the model’s ability to predict variables different from the mean and gives the proportion of the initial variance accounted for by the model [43] . PWRMSE is implicitly a measure of the comparison of the magnitudes of the peaks, volumes, and times of peak of the simulated and measured hydrographs.
(no fit) based on the relative range of the data. The coefficient of determination, R, known as the square of the sample correlation coefficient, ranges from 0 to 1 and describes the amount of observed variance explained by the model. A value of 0 implies no correlation, while a value of 1 suggests that the model can explain all of the observed variance. The Nash-Sutcliffe coefficient of Efficiency, ENS, measures the model’s ability to predict variables different from the mean and gives the proportion of the initial variance accounted for by the model [43] . PWRMSE is implicitly a measure of the comparison of the magnitudes of the peaks, volumes, and times of peak of the simulated and measured hydrographs.
Table 3. List of elevation criteria.
 : observed;
: observed;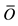 : mean observed;
: mean observed;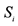 : simulated;
: simulated;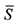 : mean simulated; n: number of data.
: mean simulated; n: number of data.
Figure 3. A three-layered FFNN with a back-propagation training algorithm.
4. Results and Discussion
4.1. Daily Streamflow Simulation by HSPF Model
The daily discharge data from 2004 to 2010 and from 2011 to 2012 were utilized for “calibration and training” and “validation and testing” the model approach, respectively. Table 4 shows the values of calibrated parameters in this study. For example, LZSN in Table 4 has the average value of 56.23 mm that has been estimated according to the Linsley equation [44] . Linsley equation for the LZSN estimation is LZSN = 100 + 0.25 × (yearly mean precipitation). For estimation of the other parameters, BASINS Technical Note 6 has been utilized [40] . Figure 4 and Figure 5 show the observed and simulated hydrographs for calibration and validation periods in HSPF model, respectively. These figures present good agreement between the daily observed and simulated runoff values in the calibration and validation periods. The correlation coefficients for calibration and validation periods are 0.83 and 0.91, respectively. It implies that HSPF simulation is acceptable. Moreover, Nash-Sutcliff coefficient (model efficiency) is 0.75 in calibration period and 0.72 in validation period. Nash-Sutcliffe efficiency coefficient values less than 0.5 are considered as unacceptable, while values greater than 0.6 are considered good and values greater than 0.8 are considered to be excellent results. Therefore, HSPF presented good daily runoff simulation. Results show that HSPF simulation of watershed discharge is acceptable in calibration period and can be used in this research.
4.2. Daily Stream Flow Simulation by ANN Model
The most common ANN network is the feed-forward network, which uses the back-propagation algorithm for training [45] . The numbers of neurons contained in the input and output layers are determined by the number of input and output variables of a given system. The size or number of neurons of a hidden layer is an important consideration when solving problems using multilayer feed-forward networks. If there are fewer neurons within a hidden layer, there may not be enough opportunity for the neural network to capture the intricate relationships between indicator parameters and the computed output parameters.
Here, we use the three-layer FFNN with one hidden layer and the common trial and error method to select the number of hidden nodes. Too many hidden layer neurons not only require a large computational time for accurate training, but may also result in overtraining. A neural network is said to be “over-trained” when the network focuses on the characteristics of individual data points rather than just capturing the general patterns presented in the entire training set.
Understanding the temporal relationships between climatic drivers and stream-flow is fundamental for the model development. Some studies use time-series correlation analysis to determine the temporal lag (number of time steps) between climate and flow variables [46] . Similar to Moradkhani et al. (2004), cross-correlation analyses were used in this study to determine the temporal relationships between precipitation, temperature and stream-flow [47] . Time-series analysis found the daily stream-flow autoregressive and moving average components to be of order 3, while the exogenous variables (precipitation and temperature) were of orders 3 and 1,
Figure 4. Analysis plot for daily flow in calibration period with HSPF model.
Figure 5. Analysis plot for daily flow in validation period with HSPF model.
Table 4. Values of parameters, used in simulation in HSPF model.
respectively. Therefore a total number of seven variables were identified as inputs (Equation (1)).
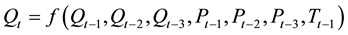 (1)
(1)
After the appropriate input vector was identified, the network was trained to predict future data based on the past and present data. In the present study, the input and output variables are first normalized linearly in the range of 0 and 1. The normalization is done using the following equation:
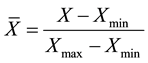 (2)
(2)
where 


Figure 6 and Figure 7 show discharge outputs of ANN model in calibration and validation periods based on observed data, respectively. A very good match is obtained between the observed runoff values and those computed by the ANN model for the training data in all the inputs. The performance of ANN model during high flows, such as in summer, autumn and winter are considered to be perfect and better than that of the HSPF model. However, during low flows, observations are a little bit above estimation. This indicates the robustness of the ANN model and confirms its capability for runoff simulation within acceptable accuracy.
Figure 6. Analysis plot for daily flow in calibration period with ANN model.
Figure 7. Analysis plot for daily flow in validation period with ANN model.
4.3. Comparison of HSPF and ANN Models
During comparison of results, the words such as “calibration” and “validation” of HSPF model were used as similar to training and testing of ANN model, respectively. To estimate the relative performance of the models in runoff simulation, values of evaluation criteria obtained from both ANN and HSPF models were compared. The evaluation criteria of ANN model obtained during calibration were compared with the corresponding evaluation criteria obtained during HSPF calibration. The values of ENS, R, ME, RMSE and PWRMSE are statistical evaluation criteria that were showed in Table 5. Similarly, the validation results of the ANN model were compared with the validation results of HSPF model.
The ENS for the HSPF model ranged from 0.64 to 0.80 for the calibration period and from 0.70 to 0.74 for the validation period. Similarly, the R for the HSPF model ranged from 0.73 to 0.88 for the calibration period and from 0.82 to 0.92 for the validation period. The ME ranged from −1.58 to 1.89 for the calibration period and from −1.15 to −0.84 for the validation period. Also, the RMSE ranged from 1.97 to 4.39 for the calibration period and from 2.09 to 3.86 for the validation period. The PWRMSE for HSPF model ranged from 2.37 to 4.52 for the calibration period and from 2.71 to 3.27 for the validation period.
The ENS for the ANN model ranged from 0.72 to 0.89 for the calibration period and from 0.78 to 0.85 for the validation period. Similarly, the R for the ANN model ranged from 0.86 to 0.93 for the calibration period and from 0.91 to 0.94 for the validation period. The ME ranged from −1.39 to 1.72 for the calibration period and from −0.97 to −0.41 for the validation period. Also, the RMSE ranged from 1.07 to 3.75 for the calibration period and from 1.89 to 2.56 for the validation period. The PWRMSE for ANN model ranged from 1.16 to 3.23 for the calibration period and from 1.23 to 2.67 for the validation period.
The results indicated that both models were generally able to simulate stream flow well during both the calibration/validation periods. However, the simulated stream flows by ANN were better than those predicted by HSPF during the calibration and validation periods. The runoff simulation of the ANN model was found to be better than the HSPF model during calibration and validation as revealed from the values of the evaluation criteria. There was a considerable difference between the values of ENS obtained from the ANN and HSPF models for the year 2004 (Table 5). Similar results were obtained during model validation period as well. In this study of the HSPF model, the values of Nash-Sutcliffe coefficients were found to be lower than that of the ANN model. This confirms that ANN model is well capable of describing the non-linear relationship between the input and output.
Figure 8 and Figure 9 show the scatter plots of observed and computed runoff values for the calibration and validation periods for the HSPF model. The scatter plot is well spread over the ideal line for this the watershed (Figure 8). In the validation period, the plot is shifted towards one side. The shift from the ideal line shows the possibility of systematic errors. Similar scatter plots for the ANN model, shown in Figure 10 and Figure 11,
Table 5. Performances of HSPF and FFNN model.
Figure 8. Scatter plot for daily flow in calibration period with HSPF model (m3/s).
Figure 9. Scatter plot for daily flow in validation period with HSPF model (m3/s).
Figure 10. Scatter plot for daily flow in calibration period with ANN model (m3/s).
Figure 11. Scatter plot for daily flow in validation period with ANN model (m3/s).
exhibit a closer scatter to the ideal line, thus indicating good runoff simulation for the Balkhichai River watershed. The scatter for the ANN model is obviously better than that of the HSPF model. These scatter plots are considered to be accounted for the application of the ANN model as is revealed by relatively more symmetrical scatter in figures. The ANN model was found to be more successful than the HSPF in relation to better forecast of peak flow. The results of this study, in general, showed that ANNs can be powerful tools in runoff simulation.
One of known advantages of the HSPF model is to make reliable flow simulation when there are available climate and soil data at ungauged site. Rainfall-runoff relation is impacted by climatic parameters and different physical e.g. slope, elevations, vegetation, soil humidity, groundwater, etc. all these parameters make a non- linear and complex relation for rainfall and runoff. Also, they have not completed data in many watersheds. Many different physical models such as HSPF have been developed, but because they cannot engage all necessary parameters, they are not as efficient as needed. Advancing use of ANN, despite its short background and the reliable results calculated by them, gives an idea of its growing popularity and bright future.
5. Conclusion
This paper reports the results of a comparison between two different models for runoff simulation in the Balkhichai River watershed in Iran, during the period of 2004-2012. The performances of models in “calibration and training” and “validation and testing” stages are compared with the observed runoff values to identify the best fit forecasting model based upon a number of selected performance criteria. The comparison results show that the ANN models have better performances in forecasting the runoff from HSPF. By considering a good training process and suitable algorithms and nodes, the prediction is more accurate. Once the architecture of the network is defined, weights are calculated so that they represent the desired output through a learning process where the ANN is trained to obtain the expected results. The neural network could predict runoff accurately, with good agreements between the observed and predicted values compared with the HSPF model. The ANNs are capable of daily simulation of runoff. However, in low flows, a little bit above estimation is observed. As in hydrological models, ANN does not require watershed information and other physical parameters in the modeling process, which reduces the complexities of modeling the system. Required time for the calibration of the ANNs is much less as compared with the HSPF. Also, for calibration, ANN model needs less expertise and experiences. In comparison to HSPF model, less data are required for simulation using the ANNs. If a number of scenarios are to be made to investigate the response of the catchment, the HSPF may prove to be advantageous in comparison to the ANNs. One of advantages of the HSPF model is to make reliable runoff simulation when there are available climate and soil data at ungauged site. In Iran, it is relatively easier to obtain flow and precipitation records through the governmental online resources compared with physical characteristics of river basins such as soil moisture, soil classes, groundwater level, infiltration and evaporation. So, the black-box models might emerge as a faster tool to implement on flow fore-casting business. The results of this study can be used for future studies, in general, the HSPF and ANN comparison in daily simulations, specifically runoff prediction performance.
References
- Kahya, E. and Dracup, J.A. (1993) US Stream Flow Patterns in Relation to the El Nino/Southern Oscillation. Water Resources Research, 28, 491-503.
- Dawson, C.W. and Wilby, R.L. (2001) Hydrological Modeling Using Artificial Neural Networks. Progress in Physical Geography, 25, 80-108. http://dx.doi.org/10.1177/030913330102500104
- Han, D., Chan, L. and Zhu, N. (2007) Flood Forecasting Using Support Vector Machine. Journal of Hydroinformatics, 9, 267-276. http://dx.doi.org/10.2166/hydro.2007.027
- Han, D., Kwong, T. and Li, S. (2007) Uncertainties in Real-Time Flood Forecasting with Neural Networks. Hydrological Processes, 21, 223-228. http://dx.doi.org/10.1002/hyp.6184
- Goel, A. (2009) ANN Based Modeling for Prediction of Evaporation in Reservoirs (Research Note). International Journal of Engineering, Transcations A: Basics, 22, 351-358.
- Banaei, F.K., Zinatizadeh, A.A.L., Mesgar, M. and Salari, Z. (2012) Dynamic Performance Analysis and Simulation of a Full Scale Activated Sludge System Treating an Industrial Wastewater Using Artificial Neutral Network. International Journal of Engineering, Transcations A: Basics, 26, 465-472.
- Nayak, P.C., Sudheer, K.P., Rangan, D.M. and Ramasastri, K.S. (2004) A Neuro-Fuzzy Computing Technique for Modelling Hydrological Time Series. Journal of Hydrology, 291, 52-66. http://dx.doi.org/10.1016/j.jhydrol.2003.12.010
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Bahramifar, A., Shirkhani, R. and Mohammadi, M. (2013) An Anfis-Based Approach for Prediction the Manning Roughness Coeffinet in Alluvial Channel at the Bank-Full Stage. International Journal of Engineering, Transcations B: Basics, 26, 177-186. http://dx.doi.org/10.5829/idosi.ije.2013.26.02b.08
- Shamseldin, A.Y. (1997) Application of a Neural Network Technique to Rainfall-Runoff Modeling. Journal of Hydrology, 199, 272-294. http://dx.doi.org/10.1016/S0022-1694(96)03330-6
- Kumar, A.R.S., Sudheer, K.P., Jain, S.K. and Agarwal, P.K. (2005) Rainfall-Runoff Modeling Using Artificial Neural Networks: Comparison of Network Types. Hydrological Processes, 19, 1277-1291. http://dx.doi.org/10.1002/hyp.5581
- Mutlu, E., Chaubey, I., Hexmoor, H. and Bajwa, S.G. (2008) Comparison of Artificial Neural Network Models for Hydrologic Predictions at Multiple Gauging Stations in an Agricultural Watershed. Hydrological Processes, 22, 5097- 5106. http://dx.doi.org/10.1002/hyp.7136
- Halff, A.H., Halff, H.M. and Azmoodeh, M. (1993) Predicting Runoff from Rainfall Using Neural Networks. In: Proceedings of the Engineering Hydrology, American Society of Civil Engineers, New York, 760-765.
- Filho, A.J.P. and dos Santos, C.C. (2006) Modeling a Densely Urbanized Watershed with an Artificial Neural Network, Weather Radar and Telemetric Data. Journal of Hydrology, 317, 31-48. http://dx.doi.org/10.1016/j.jhydrol.2005.05.007
- Zhang, B. and Govindaraju, R.S. (2000) Prediction of Watershed Runoff Using Bayesian Concepts and Modular Neural Networks. Water Resources Research, 36, 753-762. http://dx.doi.org/10.1029/1999WR900264
- Kingston, G.B., Maier, H.R. and Lambert, M.F. (2005) Calibration and Validation of Neural Networks to Ensure Physically Plausible Hydrological Modeling. Journal of Hydrology, 314, 159-176. http://dx.doi.org/10.1016/j.jhydrol.2005.03.013
- Abrahart, R.J. and See, L.M. (2007) Neural Network Emulation of a Rainfall-Runoff Model. Hydrology and Earth System Sciences, 4, 288-326. http://dx.doi.org/10.5194/hessd-4-287-2007
- Srinivasan, M.S., Hamlett, J.M., Day, R.L., Sams, J.I. and Peterson, G.W. (1998) Hydrologic Modeling of Two Glaciated Watersheds in Northeast Pennsylvania. Journal of the American Water Resources Association, 34, 963-978. http://dx.doi.org/10.1111/j.1752-1688.1998.tb01529.x
- Zarriello, P.J. and Ries III, K.G. (2000) A Precipitation-Runoff Model for Analysis of the Effects of Water Withdrawals on Streamflow, Ipswich River Basin, Massachusetts. USGS Water-Resources Investigations Report 00-4029, 99 p.
- Fontaine, T.A. and Jacomino, V.M.F. (1997) Sensitivity Analysis of Simulated Contaminated Sediment Transport. Journal of the American Water Resources Association, 33, 313-326. http://dx.doi.org/10.1111/j.1752-1688.1997.tb03512.x
- Donigian Jr., A.S., Chinnaswamy, R.V. and Jobes, T.H. (1997) Conceptual Design of Multipurpose Detention Facilities for Flood Protection and Nonpoint Source Pollution Control. Aqua Terra Consultants, Mountain View, 151 p.
- Abdulla, F., Eshtawi, T. and Assaf, H. (2009) Assessment of the Impact of Potential Climate Change on the Water Balance of a Semi-Arid Watershed. Water Resources Management, 23, 2051-2068. http://dx.doi.org/10.1007/s11269-008-9369-y
- Al-Abed, N.A. and Whiteley, H.R. (2002) Calibration of the Hydrological Simulation Program Fortran (HSPF) Model Using Automatic Calibration and Geographical Information Systems. Hydrological Processes, 16, 3169-3188. http://dx.doi.org/10.1002/hyp.1094
- Tokar, A.S. and Markus, M. (2000) Precipitation-Runoff Modelling Using Artificial Neural Networks and Conceptual Models. Journal of Hydrologic Engineering, 4, 232-239. http://dx.doi.org/10.1061/(ASCE)1084-0699(1999)4:3(232)
- Morid, S., Gosain, A.K. and Keshari, A.K. (2002) Comparison of the SWAT Model and ANN for Daily Simulation of Runoff in Snowbound Ungauged Catchments. Proceedings of the Fifth International Conference on Hydro Informatics, Cardiff, 1-5 July 2002.
- Srivastava, P., McNair, J.N. and Johnson, T.E. (2006) Comparison of Process-Based and Artificial Neural Network Approaches for Streamflow Modelling in an Agricultural Watershed. Journal of the American Water Resources Association, 42, 545-563. http://dx.doi.org/10.1111/j.1752-1688.2006.tb04475.x
- Lee, H., Lin, Y. and Chiu, Y. (2006) Quantitative Estimation of Reservoir Sedimentation from Three Typhoon Events. Journal of Hydrologic Engineering, 11, 362-370. http://dx.doi.org/10.1061/(ASCE)1084-0699(2006)11:4(362)
- Wang, P.F., Skahill, B., Samaitis, H. and Johnston, R. (2002) GIS-Based Artificial Neural Network and Processed- Based HSPF Model for Watershed Runoff in Sinclair and Dyes Inlet, WA. Proceedings of the Water Environment Federation, Watershed, 1547-1564.
- Crawford, H.H. and Linsley, R.K. (1966) Digital Simulation in Hydrology: Stanford Watershed Model IV. Technical Report No. 39, Department of Civil and Environmental Engineering, Stanford University, Stanford.
- Donigian, A.S. and Davis, H.H. (1978) User’s Manual for Agricultural Runoff Management (ARM) Model. EPA- 600/3-78-080, USEPA, Athens, GA, 112 p.
- Donigian, A.S. and Crawford, N.H. (1976) Modelling Nonpoint Pollution from the Land Surface. EPA/600/3-76-083, Environmental Research Laboratory, Athens.
- Hydrocomp, Inc. (1977) Hydrocomp Water Quality Operations Manual. Hydrocomp, Inc, Palo Alto.
- Donigian Jr., A.S. and Huber, W.C. (1991) Modeling of Nonpoint Source Water Quality in Urban and Non-Urban Areas. EPA-600/3-91-039, USEPA, Athens, GA, 78 p.
- Donigian Jr., A.S., Bicknell, B.R. and Imhoff, J.C. (1995) Hydrological Simulation Program―FORTRAN (HSPF). In: Singh, V.P., Ed., Computer Models of Watershed Hydrology, Water Resources Pubs, Highlands Ranch, 395-442.
- Bicknell, B.R., Imhoff, J.C., Kittle, J.L., Jobes, T.H. and Donigian, A.S. (2005) Hydrological Simulation Program FORTRAN. Version 12.2, User’s Manual.
- Albek, M., Ogutveren, U. and Albek, E. (2004) Hydrological Modeling of Seydi Suyu Watershed (Turkey) with HSPF. Journal of Hydrology, 285, 260-271. http://dx.doi.org/10.1016/j.jhydrol.2003.09.002
- Mark, S.J., William, F.C., Vishal, K.M., Tammo, S.S., Erin, S.B. and Jan, B. (2003) Application of Two Hydrologic Models with Different Runoff Mechanisms to a Hillslope Dominated Watershed in the Northeastern US: A Comparison of HSPF and SMR. Journal of Hydrology, 284, 57-76. http://dx.doi.org/10.1016/j.jhydrol.2003.07.005
- Bicknel, B.R., Imhoff, J.C., Kittle, J.L., Donigian, A.S. and Johanson, R.C. (1993) Hydrological Simulation Program- Fortran User’s Manual for Release 10. EPA/600/R-93/174, Environmental Research Laboratory Office of Research and Development, US Environmental Protection Agency, Athens.
- Donigian, A.S., Imhoff, J.C., Bicknell, B.R. and Kittle, J.L. (1984) Application Guide for Hydrological Simulation Program-Fortran (HSPF). EPA-600/3-84-065, United States Environmental Protection Agency, Athens, GA.
- EPA (2001) BASINS Technical Note 6, Estimating Hydrology and Hydraulic Parameters for HSPF, US.
- Eluyode, O.S. and Akomolafe, D.T. (2013) Comparative Study of Biological and Artificial Neural Networks. European Journal of Applied Engineering and Scientific Research, 2, 36-46.
- De Vos, N.J. and Rientjes, T.H.M. (2005) Constraints of Artificial Neural Networks for Rainfall-Runoff Modeling: Trade-Offs in Hydrological State Representation and Model Evaluation. Hydrology and Earth System Sciences, 9, 111- 126. http://dx.doi.org/10.5194/hess-9-111-2005
- Nash, J.E. and Sutcliffe J.V. (1970) River Flow Forecasting through Conceptual Models Part I―A Discussion of Principles. Journal of Hydrology, 10, 282-290. http://dx.doi.org/10.1016/0022-1694(70)90255-6
- Linsley, R.K., Kohler, M.A. and Paulhus, J.L.H. (1988) Hydrology for Engineers. McGraw-Hill, New York.
- Bougadis, J., Adamowski, K. and Diduch, R. (2005) Short-Term Municipal Water Demand Forecasting. Hydrological Processes, 19, 137-148. http://dx.doi.org/10.1002/hyp.5763
- Cigizoglu, H.K. (2005) Generalized Regression Neural Network in Monthly Flow Forecasting. Civil Engineering and Environmental Systems, 22, 71-81. http://dx.doi.org/10.1080/10286600500126256
- Moradkhani, H., Hsu, K.-L., Gupta, H.V. and Sorooshian, S. (2004) Improved Streamflow Forecasting Using Self- Organizing Radial Basis Function Artificial Neural Networks. Journal of Hydrology, 295, 246-262. http://dx.doi.org/10.1016/j.jhydrol.2004.03.027
NOTES
*Corresponding author.














