Received 8 September 2015; accepted 30 November 2015; published 3 December 2015

ABSTRACT

This paper proposes a system representation for unifying control design and numerical calculation in nonlinear optimal control problems with inequality constraints in terms of the symplectic structure. The symplectic structure is derived from Hamiltonian systems that are equivalent to Hamilton-Jacobi equations. In the representation, the constraints can be described as an input- state transformation of the system. Therefore, it can be seamlessly applied to the stable manifold method that is a precise numerical solver of the Hamilton-Jacobi equations. In conventional methods, e.g., the penalty method or the barrier method, it is difficult to systematically assign the weights of penalty functions that are used for realizing the constraints. In the proposed method, we can separate the adjustment of weights with respect to objective functions from that of penalty functions. Furthermore, the proposed method can extend the region of computable solutions in a state space. The validity of the method is shown by a numerical example of the optimal control of a vehicle model with steering limitations.

Keywords:

Optimal Controls, Nonlinear Systems, Constrained Systems, Symplectic Numerical Methods, Stable Manifold Method

1. Introduction

An optimal control is one of the most important strategies in control design. Optimal control problems for nonlinear systems can be formulated by Hamilton-Jacobi equations [1] . Although a lot of approximate methods were presented (see [3] ), a precise solving method of the equations had been left undeveloped for a long time. As it is now a definitive numerical solver called the stable manifold method was recently presented by [2] , and it has been applied to many practical problems [3] . The stable manifold method is a symplectic numerical scheme of equivalent Hamiltonian systems derived from the Hamilton Jacobi equations.

On the other hand, almost all actual control systems possess not only nonlinearity, but also constraints with respect to, e.g., inputs or state variables. Constrained optimal problems have attracted a lot of attentions, and many methods, e.g., the penalty method or the barrier method have been proposed for such systems [4] [5] . The common strategy of such approaches is to create constraints by rapidly increasing nonlinear weights in cost functions for preventing states from violating constraints. This idea has been widely applied in various situations, and yielded many useful results, e.g., [6] - [12] . However, in nonlinear optimal control problems with constraint, approaches based on numerical solutions obtained from the stable manifold method have not been sufficiently discussed yet to our knowledge.

This paper proposes the formulation for integrating inequality constraints in the nonlinear optimal regulator design using the stable manifold method. The formulation is derived from the input-output linearization technique [11] [13] . We can apply the stable manifold method to input affine first order nonlinear system. For such a system, solutions can be numerically calculated even if analytical solutions are not available or their behaviors are very complex. Thus, the usual control design procedure of the stable manifold method can be seamlessly applied to constrained systems described by the proposed formulation. The optimality of the controllers can be proven in the same way of the barrier method. Indeed, we show that the change caused by the transformation can be interpreted as the addition of another penalty in objective functions.

Furthermore, our formulation has the following three advantages. First, a heuristic parameter tuning of weights is practically required for convergence of calculations in many cases. However, in conventional methods, the weights of error functions such as quadratic terms with respect to states or inputs and penalty functions are described as a single objective function. Thus, it is difficult to independently adjust each weight, because solutions in nonlinear optimizations are quite sensitive with respect to such a change. In our method, the constraint is described as a part of control systems by using the transformation between inputs and state variables; therefore, the weights can be separately adjusted. Second, in the barrier method (or the interior penalty method), it is not so easy to set initial states of numerical calculations in a constrained region in some cases. In the stable manifold method, optimal orbits are calculated from a stable point at the origin to the surrounding area of the origin in the inverse direction of time evolutions. Therefore, we can systematically search solutions intersecting a given initial condition. Third, cost functions with Lagrange multiplier are used for incorporating equality constraints in addition to penalty functions in the multiplier method. The method is based on a local optimality, i.e., the Karush-Kuhn-Tucker condition, and solutions are approximately calculated by an iterative calculation, e.g., the sequential quadratic programming method [14] . In our method, optimal orbits obtained from the stable manifold method can be regarded as (semi-)global optimal solutions if they sufficiently cover a state space. Furthermore, there is no need to employ any approximation of solutions and any system reduction in the design.

This paper is constructed as follows: Section 2 states basic definitions of nonlinear optimal control problems and provides the brief introduction of our method. In Section 3, we first present a formulation of nonlinear optimal control problems with constraints in terms of differentiable saturation functions. Next, an augmented system including the constraints is introduced from the formulation. Then, we discuss three topics: the implementation of the system with the stable manifold method, the optimality of the formulation, and the extension to multi-input and multi-constraint cases. Finally, in Section 4, a numerical control example for a vehicle model with steering limitations modeled by a saturation function is illustrated to show the validity of our method.

2. Problem Setting and Brief Summary of Proposed Method

In this section, we make a brief summary of nonlinear optimal control problems and formalize a class of control systems with constraints described by inequalities.

2.1. Control Systems with Inequality Constraints

Let us consider the following nonlinear system:

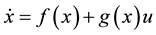(1)

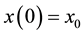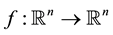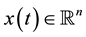with an initial condition, where and are the vector fields consisting of smooth functions, and the state and the input are denoted by, respectively, and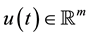. The vector representation of system (1) is as follows:

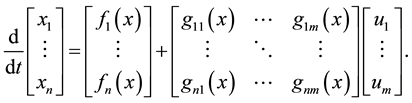(2)

Then, we consider the following constraint with respect to a state variable 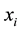for some:

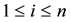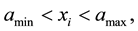(3)

where 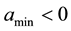and 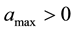are constants.

Our method has been constructed with a mind to be applied to the stable manifold method [2] . Hence, we assume the following conditions that are required for the application.

Assumption 1. System (1) satisfies

1.,

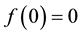2. The approximate linear system of (1) is stabilizable.

2.2. Nonlinear Optimal Regulator

We first recall the standard setting of nonlinear optimal control problems.

Problem 1. Find a control input u in (1) minimizing the objective function

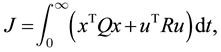(4)

where the weights Q and R are diagonal matrices such that 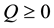and.

The Hamiltonian H in the variational calculus of the above problem can be introduced by using Lagrange multiplier as follows:

(5)

That is, Problem 1 can be rewritten as the problem of minimizing H. Then, from the stationary condition with respect to u, we obtain the optimal feedback as follows:

(6)

By substituting (6) into (5) and using dynamic programming, we get the following Hamilton-Jacobi equation:

(7)

If we can solve (7) with respect to x and p, then the solution of (7) can determine the optimal gain in the feedback (6) for each state at a time.

The stable manifold method, which is the main tool in this paper, is an integral recursion formula for calculating solutions of the Hamiltonian systems that are transformed from the Hamilton-Jacobi Equation (7) that are directly difficult to solve (see Appendix).

2.3. Conventional Methods for Constrained Optimal Problems

The penalty method and the barrier method are extended optimization methods for treating constraints. In these methods, the penalty function and the barrier function such as

(8)

(9)

are respectively added to the cost function (4), where S is the domain within the constraint, denotes the internal of S, and means that the infimum of a certain norm between x and any tends to be zero. becomes larger when x get more further away from the unconstrained region S; therefore, it is expected that solutions avoid violating constraints. However, the constraint is not exactly guaranteed, and the behaviors are depend on the setting of weights multiplied to. is defined only in the internal of S. Initial conditions in numerical calculations should be selected to satisfy this constraint, and this setting is not always easy.

2.4. Concept of Proposed Method

This section briefly summarizes the proposed method for applying the stable manifold method to nonlinear optimal problems with inequality constraints. The main idea of the method is to transform the problem as a standard problem for unconstrained systems. That is, we derive an input transformation that acts as the constraints with respect to a state from the input-state linearization [11] [13] .

Let us consider the original control system, and the input transformer that is added to (see Figure 1). has the input u and the full-state output y, and has the external input and the output that is defined as the function u of x and that realizes the constraint (e.g., in Figure 2, details will be explained later) as follows:

(10)

where is defined by using the virtual variable as

(11)

and and are given by, respectively,

(12)

The input of, i.e., the output of is designed for realizing the constraint (3). Hence, we only have to solve the standard nonlinear optimal control problem of the transformed system instead of that of the system with the constraints.

Example 1. Let us consider the nonlinear system

(13)

under the constraint. By using a smooth function in Figure 2, which will be formally defined as a differentiable saturation function in the next section, with the range, a sufficiently small number and a new state, the inequality constraint can be written by. We have the following equivalent equation of the description (see Proposition 1):

(14)

On the other hand, by substituting the relation of the system (13) into (14), the following relation is given:

(15)

where in the right side of (15) has been regarded as a new input. Hence, we can augment the system (13) as follows:

Furthermore, we can reduce this expression by eliminating as follows:

(16)

This system actually includes the inequality constraint. Moreover, the system (16) is an input affine first order nonlinear system, and it satisfies Assumption 1. Hence, we can apply the stable manifold method to the nonlinear optimal control problem of (16) instead of (13) with the constraint. In this case, the objective function is given as

(17)

where Q and R are some weight matrices, and we have defined the state variables.

3. Formulation of Nonlinear Optimal Control Problem with Constraints for Stable Manifold Method

In this section, we formally state the formulation of the previously discussed basic concept for constrained systems, and then we prove the optimality of the formulation. Finally, we show that the formulation is generalized for multi-input-output systems with higher relative degrees.

3.1. Differentiable Saturation Function

For simplification, we first introduce the standard formulation for single-input-output systems (1) with the constraint (3) from [11] . We shall introduce the following well-known definition [13] as a preparation for the generalization.

Definition 1. Let y be the output of the system (1). We call the relative degree of y if is the minimum integer satisfying, where is the Lie derivative of with respect to defined by

(18)

and we denote for.

In this paper, we consider the following function describing inequality constraints.

Definition 2. Let be the output of the system (1) with the relative degree for some. Consider a function satisfying the following properties:

1. -class,

2. bijective,

3. and, and

4. there exists a constant such that for any.

We call such an a -th differentiable saturation function.

Proposition 1. The state constrained by (3) of the system (1) for some can be described as

(19)

for any.

Proof. If (3) holds, there exists a unique z satisfying (19), because is a bijection. Conversely, if there exists z satisfying (19),. Therefore, satisfies (3). ,

Proposition 2. Consider a k-th differentiable saturation function describing the constraint (3). Then, for any integer, (19) is equivalent to the following two equations:

(20)

where for some and are functions of the time t, the k-th order time derivative of and are denoted by and, respectively.

Proof. By integrating the both side of with respect to t, we get

(21)

where is some constant of integration. Here, if we set as an initial condition, then and (21) is equal to

(22)

In the same way of the integration for each l, we can see that (20) is equal to (19). ,

Thus, we use the relation (20) instead of the inequality constraint (3) in the nonlinear optimal control design.

Remark 1. In Definition 2, the function is defined as a bijection. The surjectivity can be relaxed by restricting a state space to some open subdomain including the origin. The injectivity is used for guaranteeing the uniqueness of solutions around the origin. If we don’t assume injective, there exist a lot of z satisfying this relation at an initial time, e.g., considering a sinusoidal wave function as a constraint or in the case of systems with cyclic coordinates. Here, we assumed the injectivity to avoid such complexities.

3.2. Augmented System Representation Including Constraints

In this section, we clarify the representation of the connected system described in Section 2.

Proposition 3. Let be the output of the system (1) with the relative degree for some. Let be a r-th differentiable saturation function describing the constraint (3) with respect to. Then, for any natural number, we can describe as follows:

(23)

where is some function.

Proof. By applying a time differentiation to (19), we get

(24)

For, (23) holds if. We assume that (23) holds for. Then, the following relation holds:

(25)

By regarding the first and second terms in (25) as, we can see that (23) holds for. Because is - class, (23) holds for any l. ,

Proposition 4. Consider the system (1) with the state constrained by (3) for some. Let be the output of the system with the relative degree. By regarding as a new input in the relation (20), we can augment the system (1) as follows:

(26)

where we assume that the initial condition is for, and we have defined

(27)

(28)

Proof. From the direct calculation of (23) for, we can obtain

(29)

Hence, we can determine u by using the second equality. ,

In Proposition 4, the subsystem with respect to z corresponds with explained in Section 2. The system (26) can be reduced as follows.

Corollary 1. The system (26) is equivalent to the following system under the assumption that the constraint in (19) holds:

(30)

where we have defined

(31)

(32)

3.3. Unifying Augmented Systems with Stable Manifold Method

Let us consider designing an optimal feedback (6) for the system (30) by using the stable manifold method. To apply the stable manifold method, we must check whether Assumption 1 holds. The first assumption obviously holds.

Lemma 1. Consider the constrained system (30). Then, holds.

Proof. In the original system (1), we assumed that, i.e., for in (2). Hence,. From the definition of differentiable saturation functions, we obtain. Hence, , and for in (23). Therefore, if, for, i.e.,. ,

Consequently, the following condition is obtained from the above fact.

Theorem 5. Consider the nonlinear optimal regulator design of the system (2) that satisfies Assumption 1 with the constraint (3) in terms of the augmented system (30). The stable manifold method can be applied to the system if the linearized system of the augmented system (30) is stabilizable.

Proof. By Corollary 1 and Lemma 1, we can prove the applicability of the stable manifold method for the system. A stable manifold is defined by the adjoint variable for a certain solution of the Hamilton-Jacobi equation. If the linearized system (30) is stabilizable, there exists the stabilizing solution of the Riccati equation corresponding to the Hamilton-Jacobi equation, and there also exists a stabilizing solution

of the Hamilton-Jacobi equation such that is asymptotic stable [15] . In this case, p derived from the stabilizing solution can be calculated by the stable manifold method. ,

Furthermore, we can derive the following Hamiltonian system from the above representation in (30) for the constrained system.

Lemma 2. Equation (7) for the system (30) can be transformed into the equivalent Hamiltonian system

(33)

One of the most important advantages of this implementation of the stable manifold method is the following symplectic property of the numerical scheme.

Proposition 6. The numerical precision on the optimality of controllers obtained from the stable manifold method for the constrained optimal problem can be checked by the condition whether the Hamiltonian, i.e., the left-side of the Hamilton-Jacobi Equation (7) is sufficiently close to zero.

Proof. The Hamilton-Jacobi equation is defined by. Therefore, by using the representation in Lemma 2, if the Hamiltonian of the equivalent Hamiltonian system (33) is approximately zero, state variables of the Hamiltonian system can be regarded as a solution of the Hamilton-Jacobi equation. ,

3.4. Optimality of Problem Setting for Augmented Systems

This section shows that the formulation using the augmented system (30) is reasonable in the sense of optimal problems.

Our purpose is to find u that is subject to minimize the cost function J in Problem 1. However, the costs with respect to and are not included in J at present. Thus, we define a new objective function as follows.

Problem 2. Find a control input u in (1) minimizing the objective function

(34)

for the augmented system (30), where the weights, R and are diagonal matrices such that, and.

The purpose of the term is to converge the input to regions that are close to the bounds of the constraints. Thus, if is sufficiently small, the effect of this term becomes negligible in the sense of the original optimal problem.

Theorem 7. If the weight in (34) and the parameter of in Definition 2 are sufficiently small, and

if the i-th components of for all are sufficiently small, then a solution of Problem 2 gives

an approximation of that of Problem 1 with arbitrary accuracy.

To prove the above theorem, we prepare the following facts.

Lemma 3. Consider and z satisfying (19). Then, when or.

Proof. According to Definition 2, is bijection. Thus, for any, there exists. At the same time, and. These are equivalent to

and. Therefore, we can see that when or. ,

Lemma 4. If the i-th components of for all are sufficiently small, the cost function (34) can be considered as the cost function (4) with the nonlinear weight

(35)

where the sketch of the function W is illustrated in Figure 3, is the monotonic decreasing positive function such that

(36)

and is the monotonic increasing positive function such that

(37)

Proof. Let be the i-th component of Q. Now, we can define

(38)

where we used the relation in Lemma 3. Therefore, Equation (34) can be rewritten as

(39)

because is sufficiently close to zero. ,

Proof of Theorem 1. From Lemma 4, we can obtain the correspondence between (4) and (34) under the assumptions. On the other hand, in the barrier method, if there exist an optimal solution for the weight of penalty functions, and if the sequence converges to some for a monotonic increasing sequence, then is the solution of optimal problems with constraints. Hence, the solutions of Problem 2 are those of optimal problems with constraints. ,

3.5. Extension to Multi-Input and Multi-Constraint Cases

In this section, we describe the basic idea of extending the previous discussion on single input systems (i.e.,) to multi-input systems (i.e.,) in the framework of the stable manifold method.

As the simplest case, if inputs are isolated with each other in their input-output relations, i.e., they do not have a common output, multi-input system representation can be defined by independently applying the same way of the single input case to each input with constraint. On the other hand, there might exist many inputs derived from a certain y by differentiations. In this case, we can actually employ the same procedure [11] . Hence, we only explain the basic idea of the extension here.

We first consider the following case of two inputs with different relative degrees for simplification.

Proposition 8. Consider the system (1). Let y be the output of the system with the relative degree with respect to and the relative degree with respect to, where and and are not related with each other through their derivatives. Then, the effect of is included in the first term of the right hand of the following equation:.

Proof. If, appears after differentiations of. If, must appeared before differentiations of y as; however, this term does not generate after further differentiations. ,

The above discussion can be easily extended to the case of multi inputs with different relative degrees.

Next, we consider the case when many inputs with the same relative degree are derived from a certain y by differentiations. In this case, u is not uniquely determined from (29), because is a -matrix. However, we can choose a representative input by using the following procedure.

Definition 3. Let be the i-th component of. Then,

(40)

and can be written as

(41)

as in (29). There exists some j satisfying in the left side of (41), because. Hence, we choose one of such j as, and define

(42)

By eliminating from the system, we can regard as a new input.

Proposition 9. Let be the output of the system (1) with the relative degree. Let be a -th saturation function describing the constraint (3) with respect to. Then, the system with the input (42) satisfies the constraint for any input under the initial condition for.

Proof. The input can be constructed in the same way in Proposition 4. Note that other inputs except for are canceled by the first term in (42). ,

As a result, in the multi constraint case, we only have to apply the above two extensions to each input, and the integration to the stable manifold method is basically the same construction of the single constraint case.

4. Numerical Example

This section shows the numerical result of the nonlinear optimal control for a vehicle model to demonstrate of the validity of the proposed method.

4.1. Control Model

Let us consider a 2-wheel vehicle model that is equivalent to a 4-wheel vehicle under the following assumptions: the characteristics of wheels are same, resistive forces except for the friction between tires and grounds are negligible, and the equilibrium point of the system is a state of a steady driving with a constant speed. The state equation of the model is given by

(43)

where the state variables, r, , and denote the slip angle at the center of gravity (COG), the yaw rate, the body angle, and the steering angle, respectively, and the following physical constant parameters are used: the mass, the speed V, the moment of inertia, the distance from front axle to COG, and the distance from rear axle to COG. Moreover, and denote the translational forces with respect to, respectively, x and y in the coordinate, and they are calculated by for that is the cornering force of each wheel, for that is the lateral force of wheels obtained from a nonlinear tire model called the magic formula [16] , for that is vertical load of wheels, and that is the slip angle of wheels as follows:

(44)

(45)

(46)

where the subscript i means the front wheel if and the rear wheel if, and we have defined the friction constant between road surfaces and tires (wet condition), the experimental parameters, and, and the gravitational acceleration.

4.2. Control Design

Let us design an optimal regulator for the vehicle model with the inequality constraint as an angle limitation of the front wheels. The purpose is to stabilize the state variables at the origin 0 under a constant speed V. The system (43) satisfies Assumption 1. By using a differentiable saturation function and a new variable z, we describe the limitation

(47)

as. From the differentiation of the both side of the relation, we obtain. If we select as an input, the relative degree of with respect to u is 1. Then, by setting, is eliminated from the system (43). Furthermore, by substituting into, is also eliminated. Hence, we have

(48)

where, and we have used

(49)

with and as a differentiable saturation function. Indeed, the model (48) is stabilizable.

4.3. Numerical Results

We solved the nonlinear optimal control problem for the system (48) with the constraint (47) by the stable manifold method. The result was compared that of the penalty method with the penalty function, where, and by numerical experimentations. In this comparison, we

reduced the difference between the both methods as far as possible by using the following small weights with respect to inputs: in (4), and and in (34). Then, the both problems can be regarded as the same problem with the cost function.

Figure 4 shows two finite sets of optimal orbits designed by the proposed method and the penalty method under the convergence condition that the Hamiltonian in (7) is sufficiently small:, where z has been replaced by in the axis of the figures for understandability. Figure 5 shows the comparison result of single optimal orbits derived from the both method. A stable manifold is as a set of all solutions consisting of the pair of a controlled optimal orbit x and an optimal gain p along the time evolution. Thus, Figure 4 and Figure 5 shows the stable manifolds projected to the state space spanned by x, although stable manifolds lie on the space with x and p coordinates. We can see that the stable manifold of the proposed method covers a wider area that is equivalent to the stabilizable region in the state space.

Figure 6 shows the time responses using the conventional and proposed method, respectively, for the initial condition in the common area of the projected stable manifolds in Figure 4:. The values of the cost functions were and, respectively. The optimality was improved by the proposed method, but the difference between them seems to be small. However, this comes as a result of the setting that the weights were chosen as a small value.

On the other hand, Figure 7 shows the time responses for the initial condition in the area where is quite near (i.e., the outside of) the projected stable manifold of the conventional method in the left graph of Figure 4, and also in the projected stable manifold of the proposed method in the right graph of Figure 4: . The motion within 0.25 seconds in the case of the penalty method oscillates; however, the tire is slipping and the stability did not lose. In this case, the values of the cost functions are and, respectively, and the optimality was more improved from the previous example.

Finally, Figure 8 shows the time responses for the initial condition in the area where is far from the projected stable manifold of the conventional method in the left graph of Figure 4 in the projected stable manifold of the proposed method in the right graph of Figure 4:. Then, the conventional method caused the unstable motion as in Figure 8. Almost all trials using the penalty method in this area not only lost optimality, but also failed stabilization.

5. Conclusion and Future Work

This paper presented a control system representation that seamlessly can be applied to a precise numerical solver of Hamilton-Jacobi equations called the stable manifold method in the optimal regulator design for nonlinear systems with inequality constraints. The representation was derived from the slack variable method and the input-output linearization technique without any approximation of solutions and any system reduction. We clarified the following four facts: how to integrate the representation to stable manifold method, the weight adjustments of error and penalty functions which can be separated in this formulation, the optimality of the formulation, and the extension of the representation to multi-input and multi-constraint cases. Finally, the validity of the method was shown by the numerical example of a vehicle model with steering limitations modeled by a saturation function.

The extensions of our method to time-variable or state-dependent constraints, practical numerical simulations using more detailed vehicle models, and discussions on the robustness of the controller obtained from our method are possible future works.

Acknowledgements

We thank the Editor and the referee for their comments. This work was supported by JSPS Grants-in-Aid for Scientific Research (C) No. 26420415, and JSPS Grants-in-Aid for Challenging Exploratory Research No. 26630197. N. Sakamoto was supported by Nanzan University Pache Research Subsidy I-A-2 for the 2015 academic year.

Cite this paper

YoshikiAbe,GouNishida,NoboruSakamoto,YutakaYamamoto, (2015) Symplectic Numerical Approach for Nonlinear Optimal Control of Systems with Inequality Constraints. International Journal of Modern Nonlinear Theory and Application,04,234-248. doi: 10.4236/ijmnta.2015.44018

References

Appendix

Stable Manifold Method

The stable manifold method calculates a solution of the Hamilton-Jacobi Equation (7) as the stable manifold of the Hamiltonian system (33).

The following information is required in the calculation of the stable manifold method:

i) Calculate a symmetric matrix P such that is a stable matrix from the Riccati equation

(50)

that is the linearized relation of the Hamilton-Jacobi equation at the origin, where the matrices are defined by, and, respectively.

ii) Calculate a matrix S that is a solution of Lyapunov equation, where, and.

iii) Transform the original system into

(51)

by the coordinate transformation

(52)

The stable manifold of (33) can be calculated by the following iteration:

i) Calculate sequences of functions, and defined by

(53)

for some parameter, where,.

ii) By the iterative calculation of (53), extend a solution along an initial vector in a plain surface spanned by P with keeping the Hamiltonian of the right side of (7) is sufficiently small.

iii) If an obtained solution from the iteration passes through a desired initial state of control systems, then the iteration is finished. If not, back to ii).