Received 30 September 2014; accepted 13 October 2014; published 27 February 2015

ABSTRACT

In conjunction with linear general integral control, this paper proposes a fire-new control design technique, named Equal ratio gain technique, and then develops two kinds of control design methods, that is, Decomposition and Synthetic methods, for a class of uncertain nonlinear system. By Routh’s stability criterion, we demonstrate that a canonical system matrix can be designed to be always Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio. By solving Lyapunov equation, we demonstrate that as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero. By Equal ratio gain technique and Lyapunov method, theorems to ensure semi-globally asymptotic stability are established in terms of some bounded information. Moreover, the striking robustness of linear general integral control and PID control is clearly illustrated by Equal ratio gain technique. Theoretical analysis, design example and simulation results showed that Equal ratio gain technique is a powerful tool to solve the control design problem of uncertain nonlinear system.

Keywords:

Equal Ratio Gain Technique, General Integral Control, Nonlinear Control, Robust Control, Output Regulation

1. Introduction

The complexity of nonlinear system challenges us to come up with systematic design methods to meet control objectives and specifications. Faced with such challenge, it is clear that we can not expect a particular method to apply to all nonlinear systems [1] . Therefore, although there were Linearization techniques, Gain scheduling technique, Singular perturbation technique, feedback linearization technique, sliding mode technique and so on, nonlinear design tools, this paper still develops a new control design technique, named Equal ratio gain technique, in conjunction with linear general integral control since integral control plays an irreplaceable role in the control domain.

For general integral control design, there were various design methods, such as general integral control design based on linear system theory, sliding mode technique, Feedback linearization technique and Singular perturbation technique and so on, presented by [2] - [5] , respectively. In addition, general concave integral control [6] , general convex integral control [7] , constructive general bounded integral control [8] and the generalization of the integrator and integral control action [9] were all developed by Lyapunov method. For illustrating the practicability and validity of Equal ratio gain technique and the good robustness of linear general integral control, this paper addresses general integral control design again.

Based on Equal ratio gain technique, this paper develops two kinds of systematic methods to design linear general integral control for a class of uncertain nonlinear system, that is, one is Decomposition method and another is Synthetic method. The main contributions are as follows: 1) a canonical system matrix can be designed to be always Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 2) as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero; 3) theorems to ensure semi-globally asymptotic stability are established in terms of some bounded information. Moreover, the striking robustness of linear general integral control and PID control is clearly illustrated by Equal ratio gain technique. All these mean that Equal ratio gain technique is a powerful tool to solve the control design problem of uncertain nonlinear system, and then makes the engineers more easily design a stable controller. Consequently, Equal ratio gain technique has not only the important theoretical significance but also the broad application prospects.

Throughout this paper, we use the notation 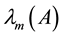and 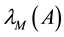to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix, for any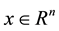. The norm of vector 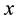is defined as, and that of matrix 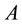is defined as the corresponding induced norm .

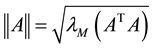The remainder of the paper is organized as follows: Section 2 demonstrates Equal ratio gain technique. Section 3 addresses the control design. Example and simulation are provided in Section 4. Conclusions are given in Section 5.

2. Equal Ratio Gain Technique

Consider the following 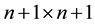system matrix,

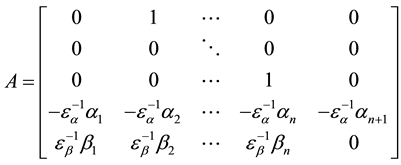
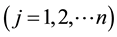
where, , 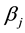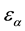and are all positive constants. If and are viewed as the controller and integrator gains, respectively, and then the system matrix is an -order single input single output linear system matrix with linear general integral control. In consideration of the controllable canonical form of linear system, the system matrix can be called as the controllable canonical form with linear general integral control.

For developing Equal ration gain technique, firstly, we must ensure that the system matrix is Hurwitz for all and, secondly we need to solve the Lyapunov equation with any given positive define symmetric matrix to obtain the solution of the matrix.

2.1. Hurwitz Stability

For and, Hurwitz stability of the system matrix can be achieved by Routh’s stability criterion, as follows:

Step 1: the polynomial of the system matrix with is,

(1)

By Routh’s stability criterion, the gains and can be chosen such that the polynomial (1) is Hurwitz. Obviously, if and are all large to zero, and then the necessary condition, that is, the coefficients of the polynomial (1) are all positive, is naturally satisfied.

Step 2: based on the gains, and Hurwitz stability condition to be obtained by Step 1, the maximums of and, that is, and, can be obtained, respectively. Since and interact, there exist innumerable and, but is more important than. Thus, two kinds of typical cases are interesting, that is, one is that is evaluated with; another is that let, and then can be obtained together.

Step 3: by and obtained by Step 2, check Hurwitz stability of the system matrix for all and. If it does not hold, redesign and and repeat the previous steps until the system matrix is Hurwitz for all and.

The demonstration above is only a basic idea to ensure that the system matrix is Hurwitz. For clearly illustrating the method above, we consider two kinds of cases, that is, and, respectively, as follows:

Case 1: for, the polynomial (1) is,

(2)

By Routh’s stability criterion, if, , , , and are all positive constants, and the following inequality,

(3)

holds, and then the polynomial (2) is Hurwitz.

Sub-class 1:, and are multiplied by, and then substituting them into (3), obtain,

(4)

By the inequality (4), obtain,

Sub-class 2:, , , and are multiplied by, and then substituting them into (3), obtain,

(5)

For this sub-class, there are two kinds of cases:

1) if, and then by the inequality (5), obtain,

2) if, and then by the inequality (5), obtain,

Case 2: for, the polynomial (1) is,

(6)

By Routh’s stability criterion, if, , , , , and are all positive constants, and the following inequality,

(7)

holds, and then the polynomial (6) is Hurwitz.

Sub-class 1:, , and are multiplied by, and then substituting them into (7), obtain,

(8)

By the inequality (8), obtain,

Sub-class 2:, , , , , and are multiplied by, and then substituting them into (7), obtain,

For this sub-class, although the situation is complex, a moderate solution can still be obtained, that is,

From the demonstration above, it is obvious that for, and or of the system matrix, there all exist such that the system matrix is Hurwitz for all. Moreover, Hurwitz stability condition is more and more complex as the order of the system matrix increases. Therefore, for the high order system matrix, the same result can be still obtained with the help of computer. Thus, we can conclude that the -order system matrix can be designed to be Hurwitz for all and. As a result, the following theorem can be established.

Theorem 1: There exist and such that the system matrix for is Hurwitz, and then it is still Hurwitz for all and.

Discussion 1: From the system matrix, the polynomial (2) and Hurwitz stability condition (3), it is not hard to see that: 1) when, the control law is reduced to PID control; 2) for, if is less than zero, and then Hurwitz stability condition can still be satisfied. However, for PID control, is the necessary condition. This means that linear general integral control is more robust than PID control.

Discussion 2: From the polynomial (1), it is not hard to see that that Hurwitz stability of the system matrix can still be achieved for and, or and. Therefore, the stability condition of Theorem 1 can be relaxed, but this is useless for the control design.

Discussion 3: From the statements above, Hurwitz stability condition is more and more complex as the order of the system matrix increases. So, although Theorem 1 is demonstrated by the single variable system matrix, it is easy to extend Theorem 1 to the multiple variable case since there is not any difficulty to ensure that as any row controller gains, or controller and its integrator gains increase with the same ratio, the system matrix is always Hurwitz in theory, that is, Routh’s stability criterion applies to not only the single variable system matrix but also the multiple variable one. Thus, the following proposition can be concluded.

Proposition 1: A canonical system matrix can be designed to be always Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio.

2.2. Solution of Lyapunov Equation

By Hurwitz stability condition given by Subsection 2.1, the system matrix can be ensured to be Hurwitz for all and. Thus, by linear system theory, if the system matrix is Hurwitz, and then for any given positive define symmetric matrix there exists a unique positive define symmetric matrix that satisfies Lyapunov equation. Thus, the solution of Lyapunov equation can be obtained by skew symmetric matrix approach [10] , that is,

where

, and

The inversion of the system matrix with is,

(9)

where the elements are omitted since it is useless to achieve our object. The interesting reader can evaluate them by.

It is well known that the solution of Lyapunov equation is more and more complex as the order of the system matrix increases. Therefore, for clearly showing the results, we consider a simple case, that is, taking and of the system matrix. Thus, taking, obtain,

and

where

and then we have,

Case 1:, and are multiplied by, and then we have,

It is obvious that and all tend to the constants as, and then we have,

where and

Case 2:, , , and are multiplied by, and then we have,

It is obvious that and all tend to the constants as, and then we have,

where and.

From the statements above, it is easy to see that for and or of the system matrix, and can all be formulated as the linear form on and all tend to zero as. Moreover, the solution of the matrix is more and more complex as the order of the system matrix increases. Thus,

by the inversion matrix (9), and can all be formulated as the linear form on for the -order system matrix, and with the help of computer, it can be verified that the solutions of and still tend to the constants as. Therefore, for the n+1-order system matrix, we can conclude that as for all, and as. As a result, the following theorem can be established.

Theorem 2: If there exist the gains and such that the -order system matrix is Hurwitz for all and, and then we have,

1) as.

2) as.

where

Discussion 4: Theorem 1 and 2 are all obtained by multiplying the controller gains and the integrator gains by the same ratios and, respectively, even under the typical cases can be equal to 1 or. This is the reason why our method is called as Equal ratio gain technique.

Discussion 5: From the statements above, the solution of the matrix is more and more complex as the order of the system matrix increases. So, although Theorem 2 is demonstrated by taking and the single variable system matrix, it is very easy to extend Theorem 2 to any given positive define symmetric matrix and the multiple variable system matrix with the help of computer since there is not any difficulty to obtain the solution of the matrix in theory, that is, Lyapunov equation applies to not only the single system matrix but also the multiple system matrix. Thus, there is the following proposition.

Proposition 2: As any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero.

2.3. Example

For testifying the justification of Theorems 1 and 2, and Propositions 1 and 2, we consider a 6-order two variable system matrix as follows,

The polynomial of the system matrix is,

.

where

The inversion of the system matrix is,

By the equation, it is very easy to obtain the fifteen linear equations with fifteen elements of the matrix. So, it is omitted.

Thus, taking

and,

and then by Routh’s stability criterion, the array of the coefficients of polynomial is,

where

Now, with the help of computer, we have: 1) if of the system matrix are multiplied by, and then it is still Hurwitz for all; 2) if and of the system matrix are multiplied by, and then it is still Hurwitz for all; 3) if of the system matrix are multiplied by, and then it is still Hurwitz for all; 4) if and of the system matrix are multiplied by, then it is still Hurwitz for all; 5) if and of the system matrix are multiplied by, and then it is still Hurwitz for all, and the numerical solutions of and are shown in Table 1 and Table 2, respectively; 6) if, , and of the system matrix are multiplied by, and then it is still Hurwitz for all, and the numerical solutions of and are shown in Table 3 and Table 4, respectively.

From the example above, it is obvious that: 1) for all the six cases, there all exists such that the system matrix is always Hurwitz for all; 2) as shown in Tables 1-4, the absolute values of and are all decrease as reduces. This not only verifies the results proposed by Subsection 2.1 and 2.2 but also shows that for the high order and multiple variable system matrix, it is convenient and practical with the help of computer.

3. Control Design

Consider the following controllable nonlinear system,

(10)

where and are the states; are the control inputs; is a vector of unknown constant parameters and disturbances. The functions and are uncertain nonlinear actions, and the functions and are continuous in on the control domain. We want to design the control laws and such that as.

Assumption 1: There are two unique control inputs and that satisfy the equations,

(11)

(12)

so that is the desired equilibrium point, and and are the steady-state controls that are needed to maintain equilibrium at.

Assumption 2: No loss of generality, suppose that the functions, , and satisfy the following inequalities,

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

for all, and. where, , , , , , , , , , and are all positive constants.

For the system (10), we develop two kinds of methods to design linear general integral controllers, respectively, that is, Decomposition method and Synthetic method.

3.1. Decomposition Method

The control laws and are taken as,

(21)

(22)

where, , , , , , and are all positive constants (, , and).

Thus, substituting (21) and (22) into (10), obtain two augmented systems,

(23)

(24)

By Assumption 1 and choosing to be large enough, and then setting and of the system (23), we obtain,

(25)

In the same way, we have,

(26)

Thus, we ensure that there are two unique solutions and, and then and are the unique equilibrium points of the systems (23) and (24), respectively.

Substituting (25) into (23) and (26) into (24), and then the whole closed-loop system can be rewritten as,

(27)

where, ,

,

and are and matrices, respectively, all their elements are equal to zero except for

and

.

Moreover, it is worthy to note that the functions and are integrated into and, respectively, via a change of variable. This has not influence on the results if the inequalities (13) and (14) hold and they can be taken as and, respectively, in the design. Therefore, they are omitted in all the following demonstrations.

The matrices for all and, and the matrix for all and can be designed to be Hurwitz, respectively. Thus, two quadratic Lyapunov functions,

(28)

(29)

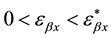
can be obtained. Where and are the solutions of Lyapunov equations

and

with any given positive define symmetric matrices and, respectively.

Thus, using as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop system (27) is,

(30)

where and.

Now, using the inequalities (15)-(20), obtain,

(31)

(32)

where, , and are all positive constants.

Substituting (31) and (32) into (30), and using and, obtain,

(33)

where, , and.

By Theorems 1 and 2, and Propositions 1 and 2, obtain,

as, as.

Therefore, there exist and such that holds for all and. Consequently, we have.

Using the fact that Lyapunov function is a positive define function and its time derivative is a negative define function if holds, we conclude that the closed-loop system (27) is stable. In fact, means, and. By invoking LaSalle’s invariance principle, it is obvious that the closed-loop system (27) is exponentially stable. As a result, we have the following theorem.

Theorem 3: Under Assumptions 1 and 2, if there exist the gains, , and such that the matrix for all and, and the matrix for all and are all Hurwitz, and then, and is an exponentially stable equilibrium point of the closed-loop system (27) for all, , and. Moreover, if all assumptions hold globally, and then it is globally exponentially stable.

In the same way, for the case of and, we have the following theorem.

Theorem 4: Under Assumptions 1 and 2, if there exist the gains, , and such that the matrix for all, and the matrix for all are all Hurwitz, and then, and is an exponentially stable equilibrium point of the closed-loop system (27) for all and. Moreover, if all assumptions hold globally, and then it is globally exponentially stable.

3.2. Synthetic Method

The control laws and are taken as,

(34)

where, , , , , , and are all positive constants.

In the same way as Subsection 3.1, the closed-loop system can be rewritten as,

(35)

where,

and is an matrix, all its elements are equal to zero except for

and

.

Moreover, by the same way as Subsection 3.1, the functions and are integrated into and, respectively.

The matrix can be designed to be Hurwitz for all, , and. Thus, a quadratic Lyapunov function,

(36)

can be obtained. Where is the solution of Lyapunov equation with any given positive define symmetric matrix.

Thus, using as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop systems (35) is,

(37)

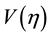
where

and

.

Now, using the inequalities (15)-(20), obtain,

(38)

(39)

where, , and are all positive constants.

Substituting (38) and (39) into (37), and using and, obtain,

(40)

where and.

By Theorems 1 and 2, and Propositions 1 and 2, obtain,

as,

as

Thus, there exist and such that

(41)

holds for all and. Consequently, we have.

Using the fact that Lyapunov function is a positive define function and its time derivative is a negative define function if the inequality (41) holds, we conclude that the closed-loop system (35) is stable. In fact, means, and. By invoking LaSalle’s invariance principle, it is easy to know that the closed-loop system (35) is exponentially stable. As a result, the following theorem can be established.

Theorem 5: Under Assumptions 1 and 2, if there exist the gains, , and such that the matrix is Hurwitz for all, , and, and then, and is an exponentially stable equilibrium point of the closed-loop system (35)

for all for all, , and. Moreover, if all assumptions hold globally, then it is globally exponentially stable.

In the same way, for the case of and, we have the following theorem.

Theorem 6: Under Assumptions 1 and 2, if there exist the gains, , and such that the matrix is Hurwitz for all and, and then, and

is an exponentially stable equilibrium point of the closed-loop system (35) for all and. Moreover, if all assumptions hold globally, then it is globally exponentially stable.

Discussion 6: From Decomposition and Synthetic methods above, it is obvious that: 1) although they are developed with two variable systems, it is not hard to extend them to the multiple variable systems; 2) as the subsystems increase, Decomposition method is simpler and more practical than Synthetic method since we can design the controllers for every subsystems, respectively, and then combine them such that the whole closed-loop system is asymptotically stable; 3) for designing a high performance controller, Synthetic method is more excellent than Decomposition method since we can use all the state variables to design the controller and integrator.

Discussion 7: From the procedure of stability analysis above, it is obvious that so long as the bounded conditions (13)-(20) are satisfied, the asymptotically stable control can be achieved. This shows that the striking feature of linear general integral control, that is, its robustness with respect to, , and, is clearly demonstrated by Equal ratio gain technique. Therefore, Equal ratio gain technique is a powerful tool to solve the control design problem of uncertain nonlinear system, and then makes the engineers more easily design a stable controller. Moreover, for the 2-order system, linear general integral control can be reduced to PID control. Thus, Equal ratio gain technique can clearly explain the reason why PID control has good robustness, too.

Discussion 8: Form all the statements of Sections 3 and 4, it is not hard to see that although Equal ratio gain technique is demonstrated by a class of special system and linear general integral control, its application is not limited in them and can be extend to solve the other relevant problem since Routh’s stability criterion, Lyapunov equation and Lyapunov method are all universal. For examples: 1) if the system is not given in the form (10), one can find a transformation matrix that takes the given system to this form if the system is controllable; 2) by combining Equal ratio gain technique with Feedback linearization technique, we can achieve the design of nonlinear integral controller; 3) as the integrator gains are equal to zero, the control is reduced to proportional control, and the similar conclusions can still be obtained.

Discussion 9: Although the design procedure above looks quite complicated, there need not abstruse theory since Routh’s stability criterion, Lyapunov equation and Lyapunov method are all simple enough to be presented in the text book and practical enough to have been used in the real-word problem. Therefore, Equal ratio gain technique has not only the important theoretical significance but also the broad application prospects.

4. Example and Simulation

Consider the pendulum system [1] described by,

where, is the angle subtended by the rod and the vertical axis, and is the torque applied to the pendulum. View as the control input and suppose we want to regulate to. Now, taking, , the pendulum system can be written as,

and then it can be verified that is the steady-state control that is needed to maintain equilibrium at the origin and the control law is,

Thus, the closed-loop system can be written as,

where

, and

.

The normal parameters are and, and in the perturbed case, and are reduced to 1 and 5, respectively, corresponding to double the mass. Thus, we have,.

Now, if the gains are taken as, , , and, and then with, and, the following inequality,

holds for all, and then the matrix is Hurwitz for all. Therefore, we have,.

By solving the Lyapunov equation with, and, obtain,

Thus, the asymptotical stability of the closed-loop system can be ensured for all. Consequently, taking, the simulation is implemented under the normal and perturbed cases, respectively. Moreover, in the perturbed case, we consider an additive impulse-like disturbance of magnitude 80 acting on the system input between 15 s and 16 s.

Figure 1 showed the simulation results under normal (solid line) and perturbed (dashed line) cases. The following observations can be made: the system responses under the normal and perturbed cases are almost identical before the additive impulse-like disturbance appears. From the simulation results and design procedure, it is obvious that by Equal ratio gain technique, we can tune a linear general integral controller with good robustness. This demonstrates that not only linear general integral control can effectively deal with the uncertain nonlinear- ity but also Equal ratio gain technique is a powerful tool to solve the control design problem of uncertain nonli-

near system, and then makes the engineers more easily design a stable controller. Consequently, Equal ratio gain technique has not only the important theoretical significance but also the broad application prospects.

5. Conclusions

In conjunction with linear general integral control, this paper proposes a fire-new control design technique, named Equal ratio gain technique, and then develops two kinds of control design methods, that is, Decomposition and Synthetic methods, for a class of uncertain nonlinear system. The main conclusions are as follows: 1) a canonical system matrix can be designed to be always Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 2) as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero; 3) theorems to ensure semi-globally asymptotic stability are established in terms of some bounded information. Moreover, the striking robustness of linear general integral control and PID control is clearly illustrated by Equal ratio gain technique. All these mean that Equal ratio gain technique is a powerful tool to solve the control design problem of uncertain nonlinear system, and then makes the engineers more easily design a stable controller. Consequently, Equal ratio gain technique has not only the important theoretical significance but also the broad application prospects.

These conclusions above are further confirmed by the design example and simulation results.

References