International Journal of Modern Nonlinear Theory and Application
Vol.03 No.05(2014), Article ID:51434,10 pages
10.4236/ijmnta.2014.35023
Conventional and Added-order Proportional Nonlinear Integral Observers
Baishun Liu, Xiangqian Luo, Jianhui Li
Academy of Naval Submarine, Qingdao, China
Email: baishunliu@163.com, qdqtlxq@sina.com, jianhui_li@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 September 2014; revised 7 October 2014; accepted 15 October 2014
ABSTRACT
In this paper, a kind of fire new nonlinear integrator and integral action is proposed. Consequently, a conventional Proportional Nonlinear Integral (P_NI) observer and two kinds of added-order P_NI observers are developed to deal with the uncertain nonlinear system. The conditions on the observer gains to ensure the estimated error to be ultimate boundness, which shrinks to zero as the states and control inputs converge to the equilibrium point, are provided. This means that if the observed system is asymptotically stable, the estimated error dynamics is asymptotically stable, too. Moreover, the highlight point of this paper is that the design of nonlinear integral observer is achieved by linear system theory. Simulation results showed that under the normal and perturbed cases, the pure added-order P_NI observer can effectively deal with the uncertain nonlinearities on both the system dynamics and measured outputs.
Keywords:
State Estimation, PI Observer, Nonlinear Integral Observer, Added-Order Observer, Nonlinear Integrator, Nonlinear integral action, Model-based Observer

1. Introduction
State observer design plays an essential role in the design of control system. Compared with most type of observers, the Proportional and Integral (PI) observers as an extension of Luenberger’s observer [1] have attracted considerable attention over the past 30 years. By using the integral information as an additional degree of freedom, PI observers can significantly improve the estimation error dynamics. Thus, the design and application of PI observer remain an interesting research topic.
The PI observer was first proposed by [2] for single input single output linear time-invariant system. After that, PI observers for linear multivariable time-varying system [3] , linear systems with unknown input disturbances [4] , linear uncertain system [5] , descriptor system [6] [7] , respectively, appeared. However, all of PI observers were designed by proportional to a linear integral of the output estimated error. Presently, P_NI observers have not been developed.
The observers for nonlinear uncertain systems mainly focus on particular classes of nonlinear systems. For the class of Lipschitz nonlinear system, an observer [8] was proposed to permit the simultaneous estimation of the states and the unknown inputs. For a class of nonlinear systems with unknown inputs, the work of [9] has proposed a high gain observer to estimate the states and unknown inputs. In [10] , a robust unknown input observer for linear and nonlinear systems was proposed in LMI formulation. An unknown input observer for a class of nonlinear uncertain system, especially consider the linear uncertainties on output matrix, was proposed by [11] and the observer design problem was solved via strong conditions. Most of the observers above were only used to deal with the system, which measured output is a linear combination of the system state, but for the nonlinear case, there are only a few results [4] [5] [7] [9] to deal with the measurement disturbances. Specially, in [9] , PI observer design was discussed for a system with constant measurement disturbances. An interesting reformulation of PI observer was given by [5] , but it is only valid for attenuating a certain bounded noise in a single output linear uncertain system. A proportional multiple integral observer for descriptor system was proposed by [7] , which allows us to decouple or attenuate measurement output disturbances. However, to the best of our knowledge, for the measured output with uncertain nonlinearities on the system states, there are no results.
Therefore, in consideration of the recent progress in the integral control domain, the development of integral observer is so far behind. This point is easy to be seen in the literatures [12] - [18] . General integral control designs based on linear system theory, sliding mode technique and feedback linearization technique were presented by [12] - [14] , respectively. In references [15] and [16] , general concave and convex integral control along with the bounded integral control actions were proposed, respectively. The method to construct general bounded integral control was presented by [17] . The generalization of integrator and integral control action appeared in [18] . All these nonlinear integral control strategies above stimulate us to develop the nonlinear integral observer and use it to deal with the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs.
Motivated by the cognitions above, this paper proposes a conventional P_NI observer and two kinds of added-order P_NI observers along with their design method, respectively. The main contributions are as follows: 1) A kind of fire new nonlinear integrator and integral action is proposed; 2) The gap that there is not nonlinear integral observer is filled by presenting three kinds of nonlinear integral observers; 3) For the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs, two solutions, that is, mixed and pure added-order P_NI observers, are provided; 4) By linear system theory and Lyapunov method, the conditions on the observer gains to ensure the estimated error to be ultimate boundness, which shrinks to zero as the states and control inputs converge to the equilibrium point, are provided. This means that if the observed system is asymptotically stable, the estimated error dynamics is asymptotically stable, too. Moreover, the highlight point of this paper is that the design of nonlinear integral observer is achieved by linear system theory.
Throughout this paper, we use the notation 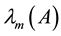 and
and  to indicate the smallest and largest eigen-
to indicate the smallest and largest eigen-
values, respectively, of a symmetric positive define bounded matrix , for any
, for any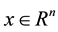 . The norm of vector
. The norm of vector
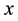 is defined as
is defined as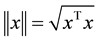 , and that of matrix
, and that of matrix 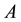 is defined as the corresponding induced norm
is defined as the corresponding induced norm
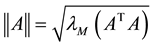 .
.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition. Section 3 addresses the design of nonlinear integral observers. Simulations are provided in Section 4. Conclusions are presented in Section 5.
2. Problem Formulation
Consider the following observable nonlinear system,
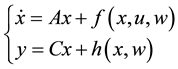 (1)
(1)
where 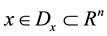 is the state,
is the state, 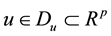 is the control input,
is the control input, 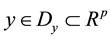 is the measured output,
is the measured output, 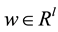 is a vector of unknown constant parameters and disturbances,
is a vector of unknown constant parameters and disturbances, 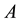 and
and  are all constant matrices.
are all constant matrices.
For convenience, we state all definitions, assumptions and theorems for the case when the equilibrium point is at the origin of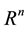 , that is,
, that is,
Assumption 1: No loss of generality, suppose that the function 


where 

For the purpose of this paper, it is convenient to introduce the following definition.
Definition 1: 



tial increasing functions [17] , 

where 
Figure 1 depicts the example curves for one component of the function belonging to the function set









3. Observer Design
This section proposes three kinds of nonlinear integral observers, respectively. First, a conventional P_NI observer is proposed to deal with the system without uncertainties in measured output; Second, a mixed added- order P_NI observer was developed for the system with the uncertain nonlinearities that appear on both the system dynamics and measured outputs; Finally, a pure added-order P_NI observer is provided to simplify the design of mixed added-order P_NI observer.
3.1. Conventional P_NI Observer
For the system (1), a conventional P_NI observer can be designed as follows,

where 


mated output; 




gain matrices; 





Thus, the error dynamics can be obtained by subtracting (3) from (1),

where 

and 

holds as




Figure 1. Example curves for one component of the function belonging to the function set
Therefore, we ensure that there is a unique solution







Assumption 2: By Assumption 1 and the definitions of 



where




Now, the design task is to provide the conditions on the gains 




is Hurwitz.
By linear system theory, a quadratic Lyapunov function 

solution of Lyapunov equation 

We use 


where
Now, using (2), (6) and (7), we have,

Substituting (4) into (8), using the inequality (9), Lyapunov equation 



where


The first term in the right-hand side of the inequality (10) is negative define when,

Furthermore, if the following inequality,

holds, it can be verified,

where
in finite time. The above argument shows that the error dynamics (4) is ultimate boundness with an ultimate
bound that decreases as 







Theorem 1: Under Assumption 1 and 2, if there exist the gain matrices 


and the inequality (11) hold, and then the error dynamics (4) is ultimate boundness with an ultimate bound that decreases as 





Discussion 1: From the error dynamics (4), it is obvious that the observer (3) is only effective for the system
with


ctively attenuated. However, when




3.2. Mixed Added-Order P_ NI Observer
For making up the shortage of conventional P_NI observer and designing an added-order P_NI observer, the system (1) needs to be added order, which is motivated by the design idea presented by [5] , as follows,

By the augmented system (15), a mixed added-order P_NI observer can be given as,

where




and the other symbols are the same as these defined in (3).
By the same way as Subsection 3.1, the error dynamics can be obtained by subtracting (16) from (15),

where
Now, the design task is to provide the conditions on the gain matrices




such that 



is Hurwitz.
Now, using (2), (6) and (7), we have,

where
By the same way as Subsection 3.1, we can obtain a quadratic Lyapunov function
then using (18), if the following inequality,

holds, we have,

and then the time derivative of 

where


and 

Thus, the trajectory of the error dynamics (17) reaches the set,
in finite time. As shown in Subsection 3.1, the following theorem can be established.
Theorem 2: Under Assumption 1 and 2, if there exist the gain matrices






and the inequality (19) hold, and then the error dynamics (17) is ultimate boundness with an ultimate bound that
decreases as 






Remark 1: It is obvious that the order of the system (15) and observer (16) are all added. This is why our observer is called the added-order observer. In addition, the observer (16) is designed by using the estimated errors 

Discussion 2: From the error dynamics (17), it is easy to see that: 1) By increasing 


























Obviously, the design method above is too complicated such that some sort of compromise is needed in practice. Therefore, a simplified observer will be proposed in the next subsection.
3.3. Pure Added-order P_ NI Observer
Based on Discussion 2, it is obvious that only the actions of 


where



are the same as these defined in (3).
By the same way as Subsection 3.2, the error dynamics can be obtained by subtracting (23) from (15),

and then by letting 
Theorem 3: Under Assumption 1 and 2, if there exist the gain matrices




hold, and then the error dynamics (24) is ultimate boundness with an ultimate bound that decreases as 






Remark 2: It is easy to see that the observer (23) is designed only by the estimated error
Discussion 3: From the error dynamics (24) and demonstration above, it is obvious that: 1)



simplified; 3) By increasing 



and
tions on system (1) but also the stability of the error dynamics is easier to be achieved. Moreover, since the integral action can attenuate measurement noise, the observer (23) can be suitable for handling measurement noise, too.
Discussion 4: Although the works of [5] [7] and the observers (15) and (23) all use the same reformulation proposed by [5] , their main differences are as follows: 1) The integral action and integrator, here they are all nonlinear, but they are all linear in [5] [7] ; 2) The observed system, here it is used to deal with the uncertain nonlinear system, however, it is used to deal with the uncertain linear system and descriptor system in [5] [7] , respectively; 3) The twice integrals of measured output and estimated one, they are used to decouple or attenuate measurement output disturbances in [7] , but this paper uses it to counteract the unknown constant uncertainties produced by the model errors, prescient constant parameters and unknown steady-state control input.
Discussion 5: Compared with the integrators and integral actions proposed by [2] - [18] , the main differences are that: 1) The integrator and integral action: here are all nonlinear; however, they are all linear in [2] - [11] , except for the reference [11] , where the diffeomorphism is used as the integrator; 2) The indispensable components to construct the integrator: here are the linear form on the estimated errors; however, they are taken as the partial derivative of Lyapunov function in [14] - [16] and a general function on all the system states in [17] [18] , respect-
tively; 3) The integral actions: here not only include bounded integral actions, such as
so contains the unbounded one; however, they are all bounded in [15] - [17] ; 4) The correlations between the integrator and integral action: here they are closely related; however, they are independent of each other in [2] - [11] and [18] . Therefore, the nonlinear integrator and integral action proposed here are fire new.
Remark 3: From the stability analysis of Subsections 3.1 - 3.3, it is obvious that: Just the integrator is taken
as the product of estimated error and reciprocal of derivative
can be transformed into the linear form on the estimated error. Just with this ingenious mathematical transformation [15] , we can use linear system theory to analyze the stability of the error dynamics with the nonlinear integral action and integrator. As a result, this is a highlight point of this paper.
4. Simulations
Consider the pendulum system [19] described by,
where



and 




measured output



linear action can be written as,
By the design method proposed here, the augmented system can be given as,
and then, the pure added-order P_NI observer can be given as,
By the design method proposed here, we can take



is Hurwitz.
Therefore, the control input can be taken as,
For demonstrating the performance of the pure added-order observer, the simulations are implemented under normal and perturbed parameter cases, respectively.
Normal case: The initial states are





Perturbed case: The initial states are







Figure 2 and Figure 3 showed the simulation results under the normal (solid line) and perturbed (dashed line) cases. As shown on Figure 2, the good control performance is still preserved, even under the perturbed case. This demonstrated that the observer (23) can be applied to the observer-based control. Figure 3 clearly shows that the estimated velocity error quickly shrinks to zero as the position tends to the equilibrium point. This not
Figure 2. System output under the normal (solid line) and per- turbed (dashed line) cases.
Figure 3. Velocity error under the normal (solid line) and per- turbed (dashed line) cases.
only verified the justification of Theorem 3 but also shows that the observer (23) has strong robustness and can effectively deal with the uncertain nonlinearities on both the system dynamics and measured outputs.
5. Conclusion
This paper proposed a conventional P_NI observer and two kinds of added-order P_NI observers along with their design method. The main contributions are as follows: 1) A kind of fire new nonlinear integrator and integral action is proposed; 2) The gap that there is not nonlinear integral observer is filled by presenting three kinds of nonlinear integral observers; 3) For the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs, two solutions, that is, mixed and pure added-order P_NI observers, are provided; 4) The conditions on the observer gains to ensure the estimated error to be ultimate boundness, which shrinks to zero as the states and control inputs converge to the equilibrium point, are provided. This means that if the observed system is asymptotically stable, the estimated error dynamics is asymptotically stable, too. In addition, the highlight point of this paper is that the design of nonlinear integral observer was achieved by linear system theory.
References
- Luenberger, D.G. (1971) An Introduction to Observers. IEEE Transactions on Automatic Control, 16, 596-620. http://dx.doi.org/10.1109/TAC.1971.1099826
- Wojciechowski, B. (1978) Analysis and Synthesis of Proportional Integral Observers for Single Input Single Output Time-Invariant Continuous Systems. Ph.D. Thesis, Gliwice.
- Kaczorek, T. (1979) Proportional Integral Observers for Linear Multivariable Time-Varying Systems. Regelungstechnik, 27, 359-362.
- Jiang, G.P., Wang, S.P. and Song, W.Z. (2000) Design of Observer with Integrators for Linear Systems with Unknown Input Disturbances. Electronics Letters, 36, 1168-1169. http://dx.doi.org/10.1049/el:20000799
- Busawon, K.K. and Kabore, P. (2001) Disturbance Attenuation Using Proportional Integral Observers. International Journal of Control, 74, 618-627. http://dx.doi.org/10.1080/00207170010025249
- Koenig, D. and Mammar, S. (2002) Design of Proportional Integral Observer for Unknown Input Descriptor Systems. IEEE Transactions on Automatic Control, 47, 2057-2062. http://dx.doi.org/10.1109/TAC.2002.805675
- Cao, Z. and Ho, D.W.C. (2004) Proportional Multiple-Integral Observer Design for Descriptor Systems with Measurement Output Disturbances. IEE Proceedings―Control Theory and Applications, 151, 279-288.
- Ha, Q.P. and Trinh, H. (2004) State and Input Simultaneous Estimation for a Class of Nonlinear Systems. Automatica, 40, 1779-1785. http://dx.doi.org/10.1016/j.automatica.2004.05.012
- Saif, M. (1993) Reduced-Order Proportional Integral Observer with Application. Journal of Guidance Control and Dynamics, 16, 985-988. http://dx.doi.org/10.2514/3.21116
- Sharifuddin, M., Goutam, C. and Kingshook, B. (2010) LMI Approach to Robust Unknown Input Observer Design for Continuous Systems with Noise and Uncertainties. International Journal of Control, Automation, and Systems, 8, 210- 219. http://dx.doi.org/10.1007/s12555-010-0205-9
- Kamel, M., Chadli, M. and Chaabane, M. (2012) Unknown Inputs Observer for a Class of Nonlinear Uncertain Systems: An LMI Approach. International Journal of Automation and Computing, 9, 331-336. http://dx.doi.org/10.1007/s11633-012-0652-2
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Linear System Theory. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, Baotou, 5, 3174-3177.
- Liu, B.S., Li, J.H. and Luo, X.Q. (2014) General Integral Control Design via Feedback Linearization. Intelligent Control and Automation, 5, 19-23. http://dx.doi.org/10.4236/ica.2014.51003
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Sliding Mode Technique. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, Baotou, 5, 3178-3181.
- Liu, B.S., Luo, X.Q. and Li, J.H. (2013) General Concave Integral Control. Intelligent Control and Automation, 4, 356- 361. http://dx.doi.org/10.4236/ica.2013.44042
- Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Convex Integral Control. International Journal of Automation and Computing, 11, 565-570.
- Liu, B.S. (2014) Constructive General Bounded Integral Control. Intelligent Control and Automation, 5, 146-155. http://dx.doi.org/10.4236/ica.2014.53017
- Liu, B.S. (2014) On the Generalization of Integrator and Integral Control Action. International Journal of Modern Nonlinear Theory and Application, 3, 44-52. http://dx.doi.org/10.4236/ijmnta.2014.32007
- Khalil, H.K. (2007) Nonlinear Systems. 3rd Edition, Electronics Industry Publishing, Beijing, 5-6.




















