International Journal of Modern Nonlinear Theory and Application
Vol.03 No.04(2014), Article ID:49978,9 pages
10.4236/ijmnta.2014.34018
Global Attractor and Dimension Estimation for a 2D Generalized Anisotropy Kuramoto-Sivashinsky Equation
Meixia Wang, Cuicui Tian, Guoguang Lin
Department of Mathematics, Yunnan University, Kunming, China
Email: zhuzhicao@163.com, 880903tc@163.com, gglin@ynu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 August 2014; revised 2 September 2014; accepted 8 September 2014
ABSTRACT
In this paper, firstly, some priori estimates are obtained for the existence and uniqueness of solutions of a two dimensional generalized anisotropy Kuramoto-Sivashinsky Equation. Then we prove the existence of the global attractor. Finally, we get the upper bound estimation of the Haus-dorff and fractal dimension of attractor.
Keywords:
Kuramoto-Sivashinsky Equation, Existence, Global Attractor, Dimension Estimation

1. Introduction
In recent years, the infinite dimension dynamic system with high dimension has been studied extensively, and the studies have obtained many achievements [1] -[8] . The related questions of its existence and uniqueness of solutions; the existence and dimension of global attractor; the existence and attraction of inertial manifolds; finite dimension, approximate inertial manifolds and time-lag inertial manifolds are still important contents that are studied.
The celebrated Kuramoto-Sivashinsky Equation
 (1.1)
(1.1)
where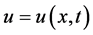 , is an Equation that for nearly half a century has attracted the attention of many researchers from various areas due to its simple but rich dynamics [9] . It first appeared in the mid-1970s by Kuramoto in the study of angularphase turbulence for a system of reaction-diffusion equations modeling the Belousov Zhabotinskii reaction in three spatial dimensions [10] .
, is an Equation that for nearly half a century has attracted the attention of many researchers from various areas due to its simple but rich dynamics [9] . It first appeared in the mid-1970s by Kuramoto in the study of angularphase turbulence for a system of reaction-diffusion equations modeling the Belousov Zhabotinskii reaction in three spatial dimensions [10] .
In a physical context, Equation (1.1) is used to model continuous media that exhibits chaotic behavior such as weak turbulence on interfaces among complex flows (quasi-planar flame front and the fluctuation of the positions of a flame front, fluctuations in thin viscous fluid films flowing over inclined planes or vertical walls, dendritic phase change fronts in binary alloy mixtures), small perturbations of a metastable planar front or interface (spatially uniform oscillating chemical reaction in a homogeneous medium) and physical systems driven far from the equilibrium due to intrinsic instabilities (instabilities of dissipative trapped ion modes in plasmas and phase dynamics in reaction-diffusion systems).
As a dynamical system the KSE is known for its chaotic solutions and complicated behavior due to the terms that appear. Namely, the 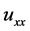 term acts as an energy source and has a destabilizing effect at a large scale, the dissipative
term acts as an energy source and has a destabilizing effect at a large scale, the dissipative 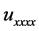 term provides dumping in small scales and, finally, the nonlinear term provides stabilization by transferring energy between large and small scales. Because of this fact, Equation (1.1) was studied extensively as a paradigm of finite dynamics in a partial differential equation. Its multi-modal, oscillatory and chaotic solutions have been investigated; its non-integrability was established via its Painlev analysis and due to its bifurcation behavior, a connection to low finite-dimensional dynamical systems is established.
term provides dumping in small scales and, finally, the nonlinear term provides stabilization by transferring energy between large and small scales. Because of this fact, Equation (1.1) was studied extensively as a paradigm of finite dynamics in a partial differential equation. Its multi-modal, oscillatory and chaotic solutions have been investigated; its non-integrability was established via its Painlev analysis and due to its bifurcation behavior, a connection to low finite-dimensional dynamical systems is established.
The generalization of KSE to two dimensions comes naturally, the two-dimensional KuramotoCSivashinsky Equation
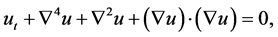 (1.2)
(1.2)
where now  and
and  Equation (1.2) has equally attracted much attention because of the same spatiotemporal chaos properties that exhibits and its applications in modeling complex dynamics in hydrodynamics [11] . Nevertheless, due to the additional spatial dimension Equation (1.2) is very challenging and even its well-posedness is still an open problem.
Equation (1.2) has equally attracted much attention because of the same spatiotemporal chaos properties that exhibits and its applications in modeling complex dynamics in hydrodynamics [11] . Nevertheless, due to the additional spatial dimension Equation (1.2) is very challenging and even its well-posedness is still an open problem.
One generalization of Equation (1.2) which is of much interest is the anisotropic two-dimensional KuramotoCSivashinsky Equation
 (1.3)
(1.3)
where the two real parameters 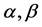 control the anisotropy of the linear and the nonlinear term, respectively, in other words, the stability of the solutions of Equation (1.3). The anisotropic two-dimensional KuramotoCSivashinsky Equation, due to the fact that it describes linearly unstable surface dynamics in the presence of in-plane anisotropy, has a wide range of applications, for instance, as a model for the nonlinear evolution of sputter-eroded surfaces and describing the epitaxial growth of a vicinal surface destabilized by step edge barriers; for further details, see the references therein, in particular [12] .
control the anisotropy of the linear and the nonlinear term, respectively, in other words, the stability of the solutions of Equation (1.3). The anisotropic two-dimensional KuramotoCSivashinsky Equation, due to the fact that it describes linearly unstable surface dynamics in the presence of in-plane anisotropy, has a wide range of applications, for instance, as a model for the nonlinear evolution of sputter-eroded surfaces and describing the epitaxial growth of a vicinal surface destabilized by step edge barriers; for further details, see the references therein, in particular [12] .
This paper focuses on the following generalization of the anisotropic KSE (1.3)
 (1.4)
(1.4)
where 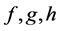 and
and  are considered as smooth functions of
are considered as smooth functions of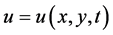 , and its study under the prism of Lie point symmetries and conservation laws [13] .
, and its study under the prism of Lie point symmetries and conservation laws [13] .
According to the above information, the paper mainly thinks about the following generalization of the anisotropic KSE (1.4)
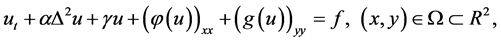 (1.5)
(1.5)
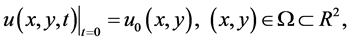 (1.6)
(1.6)
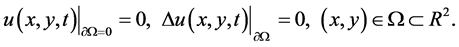 (1.7)
(1.7)
Here 




of

The following is the rest of this paper. In Section 2, we introduce some basic contents concerning global attractor. In Section 3, we obtain the existence of the global attractor, then we get the upper bound estimation of the Hausdorff and fractal dimension of the global attractor.
2. The Priori Estimate of Solution of Questions (1.5) - (1.7)
Lemma 1. Assume 





the smooth solution 

Proof. We multiply 

Here
According to Nirenberg-Gagliardo and Cauchy inequality, we obtain
From the (2.2) we obtain

Using the Gronwall inequality, the (2.1) is proved.
Lemma 2. Under the condition of Lemma 1, and 




Proof. We multiply 

Here
According to the hypothetical condition 
so
Using the Young inequality obtain
From the (2.5) we obtain
Here 
Lemma 3. Under the condition of Lemma 2, and 



Proof. We multiply 

Here
By Sobolev interpolation inequality
Noticing interpolation inequalities
so
According to the Young inequality,we can obtain
From the (2.7) we obtain
By the Gronwall inequality we can get the (2.6).
Lemma 4. Under the condition of Lemma 3, and
so the smooth solution 

Proof. We multiply 

Here
By using the Sobolev inequality
So
By the Young inequality, we obtain
From the (2.9), we obtain
So we have
3. Global Attractor and Dimension Estimation
Theorem 1. Assume that 

lution 
Proof. By the method of Galerkin and Lemma 1-Lemma 3, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.
Amusse 

and
The two above formulae subtract and obtain

We multiply 

Here
Since the assume of Lemma 1, we obtain
From the (3.2) we can obtain
According to the Gronwall inequality,we obtain
So we can get 
Theorem 2. 






1) 



2) It exists a bounded absorbing set 



3) When 


Therefor, the semigroup operators 
Theorem 3. Under the assume of Theorem 1, Questions (1.5) - (1.7) have global attractor


1)
2) 

Proof. Under the conditions of Lemma 1 - Lemma 4, it exists the solution semigroup 
From Lemma 1 - Lemma 3, to 
This shows 
Furthermore, when 

is the bounded absorbing set of semigroup
From Lemma 4, there are

bedded, which means that the bounded set in 



w-limited set of the absorptive set 
In order to estimate the Hausdorff and fractal dimension of the global attractor A of Questions (1.5) - (1.7), let Questions (1.5) - (1.7) linearize, then we obtain


where
So the solutions of Questions (1.5) - (1.7) are fully smooth. It is easy to prove the initial value, appropriate, smooth and linear Questions (3.3) - (3.4) have global and smooth solutions. Let




This suggests that 
Let 











So
Here
Theorem 4. Under the assume of Theorem 3, the global attractor 
Here 
Proof. By theorem [8] , we need to estimate the lower bound of 

Here
Under the bounded condition, 


Therefore, we can get
By 
we have
Therefore
Funding
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.
References
- Tian, L.X. (1994) Attractor of the Dissipated and Isolated Wave-Equation. Journal of Applied Mathmatics and Mechanics, 15, 539-547.
- Guo, B.L. and Li, Y.S. (1997) Attractor for Dissipative Klein-Gordon-Schrodinger Equations in R3. Journal of Differential Equations, 2, 356-377.
- Dai, Z.D., Guo, B.L. and Lin, G.G. (1998) Breakdown Structure of Generalized Kuramoto-Sivashinsky Equation Attractor. Applied Mathmatics and Mechanics, 19, 243-255.
- Du, X.Y. and Dai, Z.D. (2000) Global Attractor of Dissipative KDV Equation about Cauchy Problem. Acta Mathematica Scientia, 20, 289-295.
- Guo, B.L. (2000) The Infinite Dimension System. National Defense Industry Press, Beijing.
- Wu, J.Z., Zhao, P. and Lin, G.G. (2010) An Inertial Manifold of the Damped Boussinesq Equation. Journal of Yunnan University, 32, 310-314.
- Tian, L.X. and Ding, D.P. (2000) Local Property or Weakly Damped Forced KDV Equation in 2D Thin Domin. Journal of Jiangsu University of Science and Technology, 21 106-110.
- Lin, G.G. (2011) Nonlinear Evolution Equations. Yunnan University Press, Kunming.
- Wittenberg, R.W. (2012) Encyclopaedia of Mathematics. Supplement III, Kluwer, The Netherlands, 230-233.
- Kuramoto, Y. (1978) Diffusion-Induced Chaos in Reactions Systems. Progress of Theoretical Physics, 64, 346-367. http://dx.doi.org/10.1143/PTPS.64.346
- Galaktionov, V.A., Mitidieri, E. and Pohozaev, S.I. (2009) On Global Solutions and Blow-Up for Kuramoto-Siva- shinsky-Type Models, and Well-Posed Burnett Equations. Nonlinear Analysis: Theory, Methods & Applications, 70, 2930-2952. http://dx.doi.org/10.1016/j.na.2008.12.020
- Makeev, M.A. and Barab A.L. (1997) Ion-Induced Effective Surface Diffusion in Ion Sputtering. Applied Physics Letters, 71, 2800-2802. http://dx.doi.org/10.1063/1.120140
- Bozhkov, Y. and Dimas, S. (2013) Group Classification and Conservation Laws for a Two-Dimensional Generalized Kuramoto—Sivashinsky Equation. Journal of Nonlinear Analysis, 84, 117-135. http://dx.doi.org/10.1016/j.na.2013.02.010






































































