International Journal of Modern Nonlinear Theory and Application
Vol.3 No.1(2014), Article ID:43805,8 pages DOI:10.4236/ijmnta.2014.31003
Exponential Attractors of the Nonclassical Diffusion Equations with Lower Regular Forcing Term
Yanjun Zhang, Qiaozhen Ma*
School of Mathematics and Statistics, Northwest Normal University, Lanzhou, China
Email: 2003xbsd@163.com, *maqzh@nwnu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 19 January 2014; revised 19 February 2014; accepted 25 February 2014
ABSTRACT
In this article, we prove the existence of exponential attractors of the nonclassical diffusion equation with critical nonlinearity and lower regular forcing term. As an additional product, we show that the fractal dimension of the global attractors of this problem is finite.
Keywords
Nonclassical Diffusion Equations; Exponential Attractor; Critical Exponent; Lower Regular Forcing Term

1. Introduction
We consider the asymptotic behavior of solutions to be the following nonclassical diffusion equation:
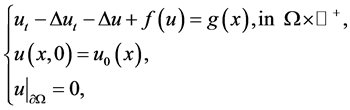 (1.1)
(1.1)
where 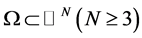 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary![]() , and the external forcing term
, and the external forcing term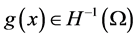 , non-linear function
, non-linear function 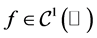 with
with  and satisfies the following conditions:
and satisfies the following conditions:
 (1.2)
(1.2)
and
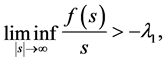 (1.3)
(1.3)
where 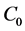 is a positive constant and
is a positive constant and 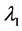 is the first eigenvalue of
is the first eigenvalue of  on
on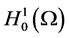 . The number
. The number 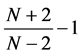 is called the critical exponent; since the nonlinearity
is called the critical exponent; since the nonlinearity  is not compact in this case, this is one of the essential difficulties in studying the asymptotic behavior.
is not compact in this case, this is one of the essential difficulties in studying the asymptotic behavior.
This equation appears as a nonclassical diffusion equation in fluid mechanics, solid mechanics and heat conduction theory, see for instance [1] -[3] and the references therein.
Since Equation (1.1) contains the term , it is different from the usual reaction diffusion equation essentially. For example, the reaction diffusion equations has some smoothing effect, that is, although the initial data only belongs to a weaker topology space, the solution will belong to a stronger topology space with higher regularity. However, for Equation (1.1), if the initial data
, it is different from the usual reaction diffusion equation essentially. For example, the reaction diffusion equations has some smoothing effect, that is, although the initial data only belongs to a weaker topology space, the solution will belong to a stronger topology space with higher regularity. However, for Equation (1.1), if the initial data ![]() belongs to
belongs to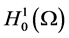 , the solution
, the solution  with
with 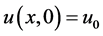 is always in
is always in  and has no higher regularity because of
and has no higher regularity because of , which is similar to the hyperbolic equation. Consequently, its dynamics would be more complex and interesting.
, which is similar to the hyperbolic equation. Consequently, its dynamics would be more complex and interesting.
The long-time behavior of the solutions of (1.1) has been considered by many researchers; see, e.g. [4] -[9] , and the references therein. For instance, for the case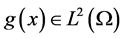 , the existence of a global attractor of (1.1) in
, the existence of a global attractor of (1.1) in 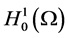 was obtained in [4] under the assumptions that
was obtained in [4] under the assumptions that 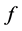 satisfies (1.2) and (1.3) corresponding to
satisfies (1.2) and (1.3) corresponding to ![]()
and the additional condition 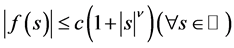 with
with , which essentially requires that the nonlinearity is subcritical. In [7] the authors investigated the existence of the global attractors for
, which essentially requires that the nonlinearity is subcritical. In [7] the authors investigated the existence of the global attractors for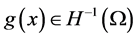 , and proved the asymptotic regularity and existence of exponential attractors for
, and proved the asymptotic regularity and existence of exponential attractors for 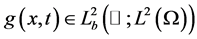 only under the conditions (1.2)-(1.3). Recently, the authors in [9] showed the asymptotic regularity of solutions of Equation (1.1) in
only under the conditions (1.2)-(1.3). Recently, the authors in [9] showed the asymptotic regularity of solutions of Equation (1.1) in  for any
for any  and for
and for
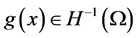 ,
, 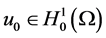 only under the assumptions (1.2)-(1.3).
only under the assumptions (1.2)-(1.3).
For the limit of our knowledge, the existence of exponential attractors of Equation (1.1) has not been achieved by predecessors for . On the other hand, we note that in [10] the authors scrutinized the asymptotic regularity of the solutions for a semilinear second order evolution equation when
. On the other hand, we note that in [10] the authors scrutinized the asymptotic regularity of the solutions for a semilinear second order evolution equation when , and based on this regularity, they constructed a family of finite dimensional exponential attractors. However, they require the following additional technical assumptions besides (1.2) and (1.3):
, and based on this regularity, they constructed a family of finite dimensional exponential attractors. However, they require the following additional technical assumptions besides (1.2) and (1.3):
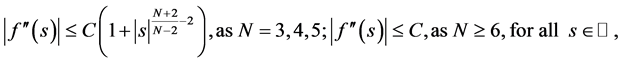
and
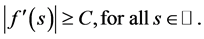
In this article, motivated by the work in [10] -[12] , based on the asymptotic regularity in [9] , we construct a finite dimensional exponential attractor of (1.1) only under the conditions (1.2) and (1.3).
Our main result is Theorem 1.1 Assume  and satisfies (1.2)-(1.3),
and satisfies (1.2)-(1.3),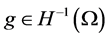 . Then the semigroup
. Then the semigroup 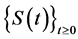 associated with problem (1.1) has an exponential attractor
associated with problem (1.1) has an exponential attractor 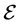 in
in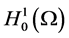 .
.
Remark 1.1 If ![]() is a global attractor of (1.1) in
is a global attractor of (1.1) in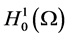 , we know that
, we know that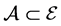 , then Theorem 1.1 implies that fractal dimension of the global attractor
, then Theorem 1.1 implies that fractal dimension of the global attractor ![]() is finite.
is finite.
2. Notations and Preliminaries
In this section, for convenience, we introduce some notations about the functions space which will be used later throughout this article.
•  with domain
with domain , and consider the family of Hilbert space
, and consider the family of Hilbert space  with the standard inner products and norms, respectively,
with the standard inner products and norms, respectively,

Especially,  means the
means the  inner product and norm, respectively.
inner product and norm, respectively.
• 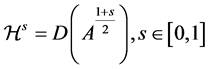 with the usual norm
with the usual norm . Especially, we denote
. Especially, we denote 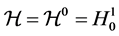 and
and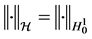 .
.
• 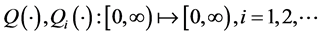 are continuous increasing functions.
are continuous increasing functions.
•  denote the general positive constants,
denote the general positive constants, 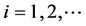 , which will be different from line to line.
, which will be different from line to line.
We also need the following the transitivity property of exponential attraction, e.g., see [[12] , Theorem 5.1]:
Lemma 2.1 ([13] ) Let 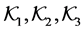 be subsets of
be subsets of ![]() such that
such that
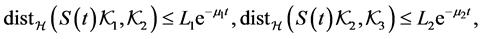
for some 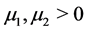 and
and . Assume also that for all
. Assume also that for all  there holds
there holds

for some 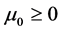 and
and . Then it follows that
. Then it follows that
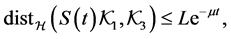
where 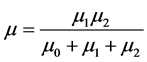 and
and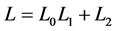 .
.
3. Exponential Attractor
In this subsection, based on the asymptotic regularity obtained in [9] , we will construct an exponential attractor by the methods and techniques devised in [10] -[12] . We first need the following Lemmas:
Lemma 3.1 ([7] ) Let  satisfies (1.2)-(1.3) and
satisfies (1.2)-(1.3) and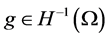 . Then for any
. Then for any  and any
and any![]() , there is a unique solution
, there is a unique solution 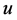 of (1.1) such that
of (1.1) such that

Moreover,the solution continuously depends on the initial data in![]() .
.
In the remainder of this section, we denote by  the semigroup associated with the solutions of (1.1)-(1.3).
the semigroup associated with the solutions of (1.1)-(1.3).
Lemma 3.2 ([7] ) Under conditions of above Lemma, There is a positive constant ![]() such that for any bounded subset
such that for any bounded subset![]() , there exists
, there exists 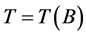 such that
such that
 (3.1)
(3.1)
From this Lemma, we know that the semigroup of operators  generalized by (1.1) possesses a bounded absorbing set
generalized by (1.1) possesses a bounded absorbing set 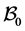 in
in![]() .
.
Lemma 3.3 Under conditions of![]() , and
, and  be two solutions of (1.1) with
be two solutions of (1.1) with , respectively, it follows that
, respectively, it follows that
 (3.2)
(3.2)
Proof Let  satisfies the following equation
satisfies the following equation
 (3.3)
(3.3)
Taking the scalar product of (3.3) with , we find,
, we find,
 (3.4)
(3.4)
From the condition (1.2), by using the Hölder inequality, and noting the embedding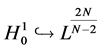 , we have
, we have
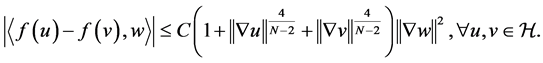
And then, by means of (3.1), we obtain
 (3.5)
(3.5)
So, combining with Equation (3.4), (3.5), we get

then using the Gronwall lemma to above inequality, we can conclude our lemma immediately.
Lemma 3.4 ([9] ) Let  and satisfies (1.2), (1.3),
and satisfies (1.2), (1.3), . Then, for any
. Then, for any
 , there exists a subset
, there exists a subset , a positive constant
, a positive constant ![]() and a monotone increasing function
and a monotone increasing function
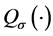 such that for any bounded set
such that for any bounded set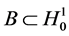 ,
,
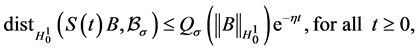 (3.6)
(3.6)
where 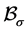 and
and 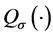 depend on
depend on 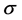 but
but ![]() is independent of
is independent of ;
; 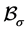 satisfying
satisfying
 (3.7)
(3.7)
for some positive constant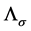 ; And
; And 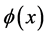 is the unique solution of the following elliptic equation
is the unique solution of the following elliptic equation
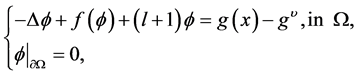 (3.8)
(3.8)
where the constant 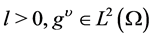 such that
such that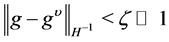 . Furthermore, we know that the solution
. Furthermore, we know that the solution 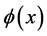 only belongs to
only belongs to  when
when 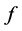 satisfies (1.2)-(1.3).
satisfies (1.2)-(1.3).
Lemma 3.5 ([9] ) Under the assumption of Lemma 3.4, for any bounded subset , if the initial data
, if the initial data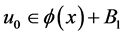 , then the solution
, then the solution 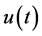 of (1.1) has the following estimates similar to (3.7) in Lemma 3.4, more precisely, we have
of (1.1) has the following estimates similar to (3.7) in Lemma 3.4, more precisely, we have
 (3.9)
(3.9)
where the constant 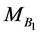 depends only on
depends only on  and the
and the 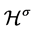 -bound of
-bound of![]() .
.
Lemma 3.6 There exists ![]() such that
such that
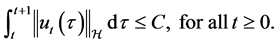 (3.10)
(3.10)
Proof For the solution  of (1.1), we now decompose
of (1.1), we now decompose  as follows
as follows
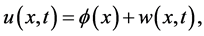 (3.11)
(3.11)
where  is a fixed solution of (3.8), and
is a fixed solution of (3.8), and 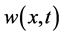 satisfies the following equation :
satisfies the following equation :
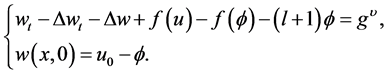 (3.12)
(3.12)
At the same time, noticing the embedding , and from Lemma 3.5 we yield
, and from Lemma 3.5 we yield
 (3.13)
(3.13)
Taking the inner product of (3.12) with![]() , we get
, we get
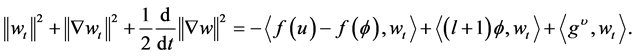 (3.14)
(3.14)
By means of (3.1) and (3.13) and together with H![]() lder, Young inequalities, it follows that
lder, Young inequalities, it follows that
 (3.15)
(3.15)

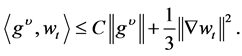
Thus, combining with (3.14), there holds

Integrating the above inequality on 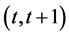 and noting
and noting , the proof completes.
, the proof completes.
Next, we will prepared for constructing an exponential attractor of 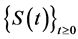 in
in ![]() by applying the abstract results devised in [10] -[12] [14] .
by applying the abstract results devised in [10] -[12] [14] .
Firstly, for each fixed , we define
, we define
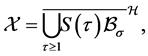 (3.16)
(3.16)
where 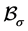 is the set obtained in Lemma 3.4. Then, from Lemma 3.5 we know that
is the set obtained in Lemma 3.4. Then, from Lemma 3.5 we know that
 (3.17)
(3.17)
Secondly, let us establish some properties of this set.
•  is a compact set in
is a compact set in , due to Lemma 3.4.
, due to Lemma 3.4.
• 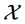 is positive invariant. In fact, from the continuity of
is positive invariant. In fact, from the continuity of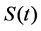 , we have
, we have
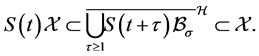 (3.18)
(3.18)
• There holds
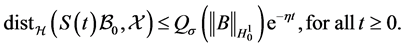 (3.19)
(3.19)
Indeed, it is apparent that
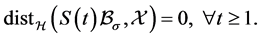 (3.20)
(3.20)
Hence, (3.19) follows from Lemma 2.1.
• There is ![]() such that
such that
 (3.21)
(3.21)
This is a direct consequence of Lemma 3.6.
Therefore such a set ![]() is a promising candidate for our purpose.
is a promising candidate for our purpose.
Finally, we need the following two lemmas.
Lemma 3.7 For every![]() , the mapping
, the mapping  is Lipschitz continuous on
is Lipschitz continuous on .
.
Proof For 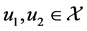 and
and  we have
we have
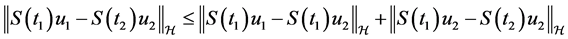 (3.22)
(3.22)
The first term of the above inequality is handled by estimate (3.2). Concerning the second one,
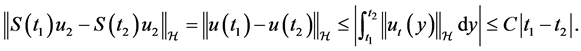 (3.23)
(3.23)
Hence, there exists a constant , such that
, such that
 (3.24)
(3.24)
On the other hands, for each initial data , we can decompose the solution
, we can decompose the solution 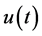 of (1.1) as
of (1.1) as
 (3.25)
(3.25)
where  and
and 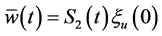 solve the following equations respectively:
solve the following equations respectively:
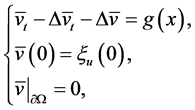 (3.26)
(3.26)
and
 (3.27)
(3.27)
Therefore, we will have the following lemma:
Lemma 3.8 The following two estimates hold:
 (3.28)
(3.28)
and
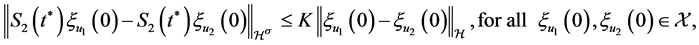 (3.29)
(3.29)
where the constant ![]() depends only on
depends only on  and
and .
.
Proof Given two solutions  of Equation (1.1) origination from
of Equation (1.1) origination from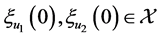 , respectively.
, respectively.
Set
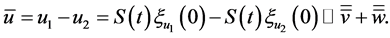
where 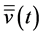 and
and  solve the following equations respectively:
solve the following equations respectively:
 (3.30)
(3.30)
and
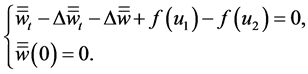 (3.31)
(3.31)
It is apparent that 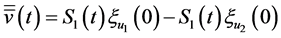 and
and 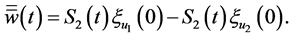
Taking the product of (3.30) with  in
in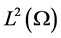 , we get
, we get
 (3.32)
(3.32)
So
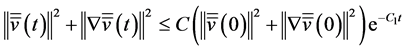 (3.33)
(3.33)
Hence, setting
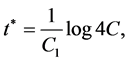 (3.34)
(3.34)
we have
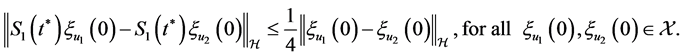
So, we obtain the result (3.28).
On the other hands, taking the product of (3.31) with 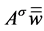 in
in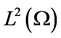 , we ge
, we ge
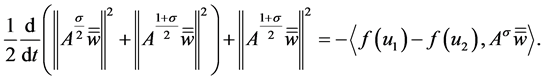 (3.35)
(3.35)
Since , we have
, we have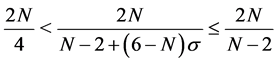 .
.
So, from (1.2) and using H![]() lder inequality, we have
lder inequality, we have
 (3.36)
(3.36)
where the constant  comes from the embedding
comes from the embedding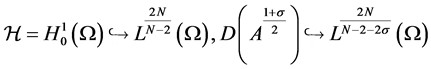 ,
, .
.
From Lemma 3.3, we obtain the inequality

and an integration on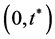 , we can get the estimate (3.29).
, we can get the estimate (3.29).
Proof of Theorem 1.1 Applying the abstract results devised in [10] -[12] , from Lemma 3.7 and Lemma 3.8, we can prove the existence of an exponential attractor 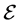 for
for 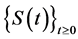 in
in  immediately.
immediately.
Remark 3.9 As a direct consequence of Theorem 1.1 and the a priori estimates given in [[9] , Lemma 3.5] and Lemma 3.8, we decompose 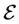 as
as , where
, where ![]() is bounded in
is bounded in 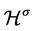 for any
for any
 and
and 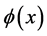 is the unique solution of (3.8).
is the unique solution of (3.8).
Acknowledgements
The authors thank the referee for his/her comments and suggestions, which have improved the original version of this article essentially. This work was partly supported by the NSFC (11061030,11101334) and the NSF of Gansu Province(1107RJZA223), in part by the Fundamental Research Funds for the Gansu Universities.
References
- Aifantis, E.C. (1980) On the Problem of Diffusion in Solids. Acta Mechanica, 37, 265-296. http://dx.doi.org/10.1007/BF01202949
- Kuttler, K. and Aifantis, E. (1988) Quasilinear Evolution Equations in Nonclassical Diffusion. SIAM Journal on Applied Mathematics, 19, 110-120. http://dx.doi.org/10.1137/0519008
- Peter, J.G. and Gurtin, M.E. (1968) On the Theory of Heat Condition Involving Two Temperatures. Zeitschrift für angewandte Mathematik und Physik ZAMP, 19, 614-627. http://dx.doi.org/10.1007/BF01594969
- Xiao, Y. (2002) Attractors for a Nonclassical Diffusion. Acta Mathematicae Applicatae Sinica, 18, 273-276. http://dx.doi.org/10.1007/s102550200026
- Wang, S., Li, D. and Zhong, C. (2006) On the Dynamics of a Class of Nonclassical Parabolic Equation. Journal of Mathematical Analysis and Applications, 317, 565-582. http://dx.doi.org/10.1016/j.jmaa.2005.06.094
- Sun, C., Wang, S. and Zhong, C. (2007) Global Attractors for a Nonclassical Diffusion Equation. Acta Mathematicae Applicatae Sinica, 23, 1271-1280.
- Sun, C. and Yang, M. (2008) Dynamics of the Nonclassical Diffusion Equations. Asymptotic Analysis, 59, 51-81.
- Sun, C. (2009) Asympotic Regularity for Some Dissipative Equations. Journal of Differential Equations, 248, 342-362. http://dx.doi.org/10.1016/j.jde.2009.08.007
- Wu, H. and Zhang, Z. (2011) Asymptotic Regularity for the Nonclassical Diffusion Equation with Lower Regular Foring Term. Dynamical Systems, 26, 391-400. http://dx.doi.org/10.1080/14689367.2011.562185
- Sun, C., Yang, L. and Duan, J. (2011) Asymptotic Behavior for a Semilinear Second Order Evolution Equation. Transactions of the American Mathematical Society, 363, 6085-6109. http://dx.doi.org/10.1090/S0002-9947-2011-05373-0
- Efendiev, M., Miranville, A. and Zelik, S.V. (2005) Exponential Attractors and Finite-Dimensional Reduction of NonAutonomous Dynamical Systems. Proceedings of the Royal Society of Edinburgh: Section A Mathematics, 135, 703- 730.
- Miranville, A. and Zelik, S.V. (2008) Attracts for Dissipative Partial Different Equations in Bounded and Unbounded Domains, In: Dafermos, C.M. and Pokorny, M., Eds., Evolutionary Equations, Elsevier, Amesterdam, 103.
- Fabrie, P., Galusinski, C., Miranville, A. and Zelik, S. (2004) Uniform Exponential Attractors for a Singularly Perturbed Damped Wave Equation. Discrete and Continuous Dynamical Systems, 10, 211-238. http://dx.doi.org/10.3934/dcds.2004.10.211
NOTES

*Corresponding author.

