International Journal of Modern Nonlinear Theory and Application
Vol.1 No.3(2012), Article ID:23082,8 pages DOI:10.4236/ijmnta.2012.13010
Adaptive Output Tracking for Nonlinear Network Control Systems with Time-Delay
College of Automation, Chongqing University of Post and Telecommunications, Chongqing, China
Email: zdyjm@163.com, zenghy99@163.com
Received August 25, 2012; revised September 11, 2012; accepted September 17, 2012
Keywords: Time-Delay; Network Control Systems; Backstepping Design; Adaptive Control; Output Tracking
ABSTRACT
The problem of adaptive output tracking is researched for a class of nonlinear network control systems with parameter uncertainties and time-delay. In this paper, a new program is proposed to design a state-feedback controller for this system. For time-delay and parameter uncertainties problems in network control systems, applying the backstepping recursive method, and using Young inequality to process the time-delay term of the systems, a robust adaptive output tracking controller is designed to achieve robust control over a class of nonlinear time-delay network control systems. According to Lyapunov stability theory, Barbalat lemma and Gronwall inequality, it is proved that the designed state feedback controller not only guarantees the state of systems is uniformly bounded, but also ensures the tracking error of the systems converges to a small neighborhood of the origin. Finally, a simulation example for nonlinear network control systems with parameter uncertainties and time-delay is given to illustrate the robust effectiveness of the designed state-feedback controller.
1. Introduction
Network control system is a real-time closed-loop feedback control system composed of sensors, controllers, actuators, etc. The advantages of network control systems are its easy installation and maintenance, and its high reliability and flexibility [1,2]. In recent decades, there are lots of progresses in the study of stability of the network control systems [3-6].
However, in the closed-loop control of the network control system, the data transmission process is often produce time-delay. The time-delay of network control system often affects the stability and performance of the system, and may even cause the instability of the entire system [7]. Therefore, the impact of the time-delay on network control system needs to be considered when studying network control systems and designing controllers. In [8], the authors analyzed the source of the time-delay of network control system. For the time-delay problem of network control system, a maximum allowable delay bound satisfying the requirement of stability was proposed in [9], and the maximum delay caused by the network was estimated in [10]. For designing controllers of network control systems, in [11], the authors discussed a class of uncertain systems’ adaptive control scheme, and in [12] authors analysis robust stability of networked control systems with uncertainty. Although some progresses are made in linear network control systems, nonlinear network control systems with parameter uncertainties and time-delay needs to be studied. For example, in [13-17], the authors study the problems of adaptive robust control for uncertain systems and highorder uncertain nonlinear systems, and analyze the stability of the systems by Lyapunov stability theory. But these papers did not consider the situation of the systems with time-delay.
Therefore, in this paper, the system is modeled as a class of nonlinear network control system with parameter uncertainties and time-delay. A new program is proposed to design controller for this system, and a robust controller is designed by using the backstepping method. According to Lyapunov stability theory, Barbalat lemma and Gronwall inequality, it is proved that the designed controller not only guarantees the state of nonlinear network control systems with parameter uncertainties and time-delay is uniformly bounded, but also ensures the tracking error of the systems converges to a small neighborhood of the origin. The rest parts of the paper are organized as follows: in Section 2, a class of nonlinear network control system is introduced, and the assumption and lemmas are proposed. In Section 3, the controller is designed by using the backstepping method. In Section 4, a simulation example is presented. Finally, a conclusion is given in Section 5.
2. Problem Description
In this paper, we consider a class of nonlinear network control systems with parameter uncertainties and timedelay, this system is described as
 (1)
(1)
where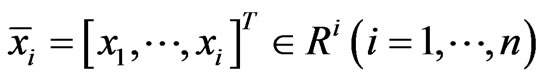 ,
, 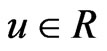 , and
, and  are respectively the states, the control input and system output,
are respectively the states, the control input and system output, 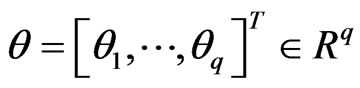 is a vector of unknown constant parameters, di(·) ≠ 0, ψi(·) and
is a vector of unknown constant parameters, di(·) ≠ 0, ψi(·) and 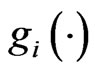 are unknown smooth functions, hi(0) = 0 (1 ≤ i ≤ n) is also an unknown smooth functions, τ is time-delay, and τ ≥ 0.
are unknown smooth functions, hi(0) = 0 (1 ≤ i ≤ n) is also an unknown smooth functions, τ is time-delay, and τ ≥ 0.
The objective of this paper is to design an adaptive feedback controller. The designed controller ensures the state of the closed-loop systems is bounded and the trajectory of output y(t) can asymptotic track reference signal yr(t).
Assumption 1 For smooth function di(t, x, u), i = 1, ···, n there exist functions 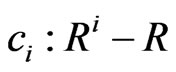 and
and  satisfies 0 < ci(x1, ···, xi) ≤ di(t, x, u) ≤ ci(x1, ···, xi + 1), xn+1 = u.
satisfies 0 < ci(x1, ···, xi) ≤ di(t, x, u) ≤ ci(x1, ···, xi + 1), xn+1 = u.
Assumption 2 Because we have hi(0) = 0, then the hi(x1(t)) can be expressed as hi(x1(t)) = γi(x1(t)), and γi(x1(t)) satisfies the following assumption
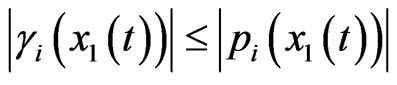
where pi(x1(t)) is a known and smooth enough function.
Lemma 1 If the real number a ≥ 0, b ≥ 0, m ≥ 1, then there exist the following inequality
 .
.
Proof for any real number x ≥ 0, y > 0, n > 0, by Young inequality, we have
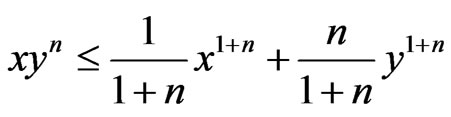 .
.
Let a = x, 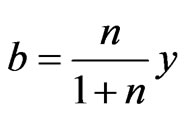 , m = n + 1 then we can release to Lemma 1.
, m = n + 1 then we can release to Lemma 1.
Barbalat lemma [18] If x(t) is a uniformly continuous function, and
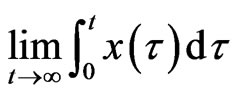
exists and is bounded, then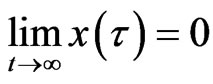 .
.
3. Adaptive Controller Design
In this section, by using the backstepping recursive method, we design a robust adaptive output tracking controller. The designed ideas of this method are described as follows: for the i-th equation of the system, constructed a suitable Lyapunov function, and designed virtual control law αi, the designed αi makes the subsystem consist of previous i equations is stable, therefore, in step n, the designed controller u which makes the system consist of n equations stability is the true controller that makes the closed-loop control systems globally stable.
Step 1 Reference signal yr is a smooth function and bounded, and its derivative 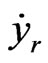 is also bounded, the output tracking error is defined by ε1 = x1 – yr.
is also bounded, the output tracking error is defined by ε1 = x1 – yr.
Constructed Lyapunov function as
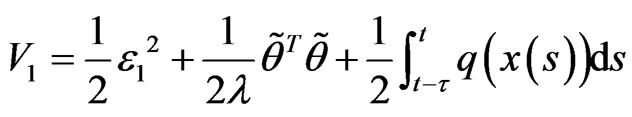 where λ are positive,
where λ are positive, 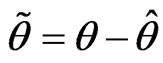 ,
, 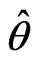 is estimates of the unknown constant parameter θ. Calculating the derivative of V1 along with system (1), we have
is estimates of the unknown constant parameter θ. Calculating the derivative of V1 along with system (1), we have
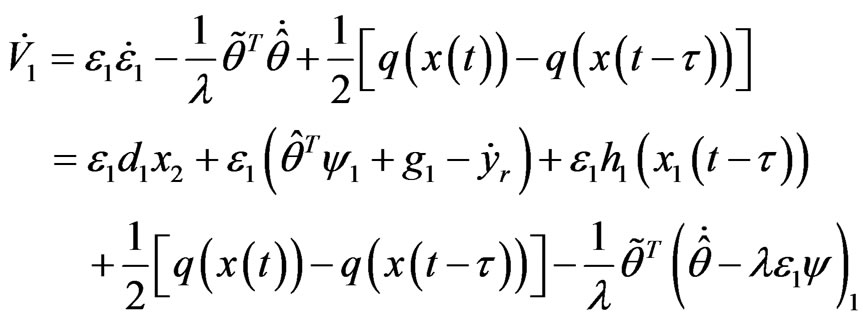 (2)
(2)
Because 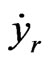 is bounded, presence non-negative smooth function
is bounded, presence non-negative smooth function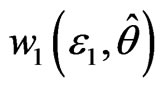 , satisfies
, satisfies
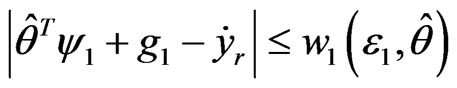 .
.
By Lemma 1, for any real number σ that greater than zero, let , b = σ, so that exists a smooth function
, b = σ, so that exists a smooth function , satisfies
, satisfies
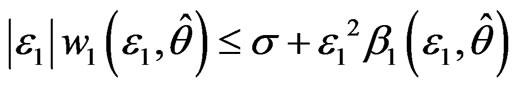 . (3)
. (3)
By using Young inequality, let constant ξ1 > 0 we have
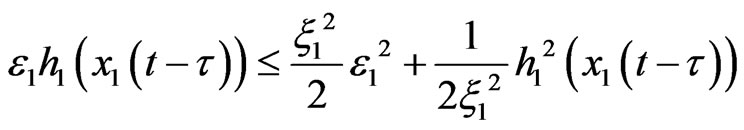 , (4)
, (4)
select 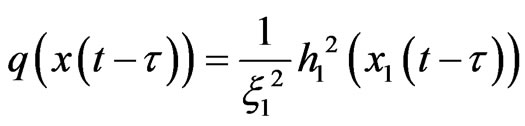 then we have
then we have
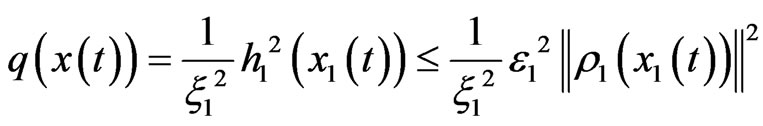 , (5)
, (5)
where ρ1(x1(t)) is a smooth function.
Let z1 = λε1ψ1, Substituting (3), (4), (5) into (2), we have

Designed virtual controller as
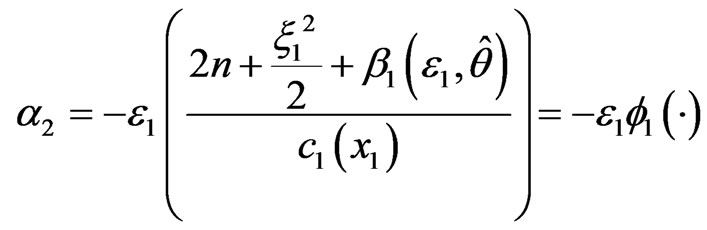 where f1(·) is smooth function that is greater than zero.
where f1(·) is smooth function that is greater than zero.
So that we can release to

And because –ε1α2 ≥ 0, by assumption 1, we have
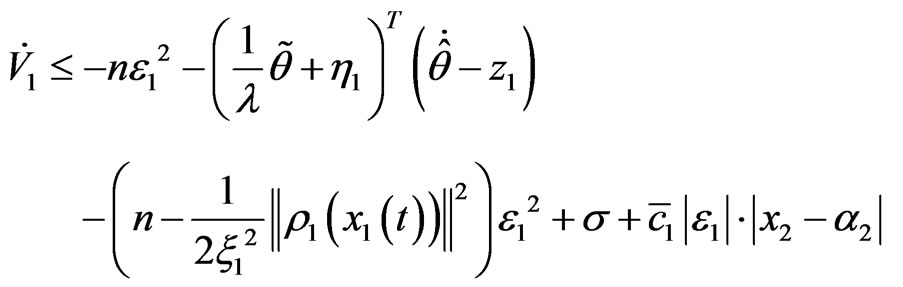
where η1 = 0.
Step 2 Let ε2 = x2 – α2, constructed Lyapunov function as
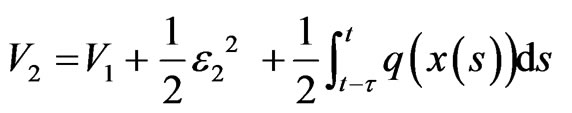
Calculating the derivative of V2 along with system (1), we have
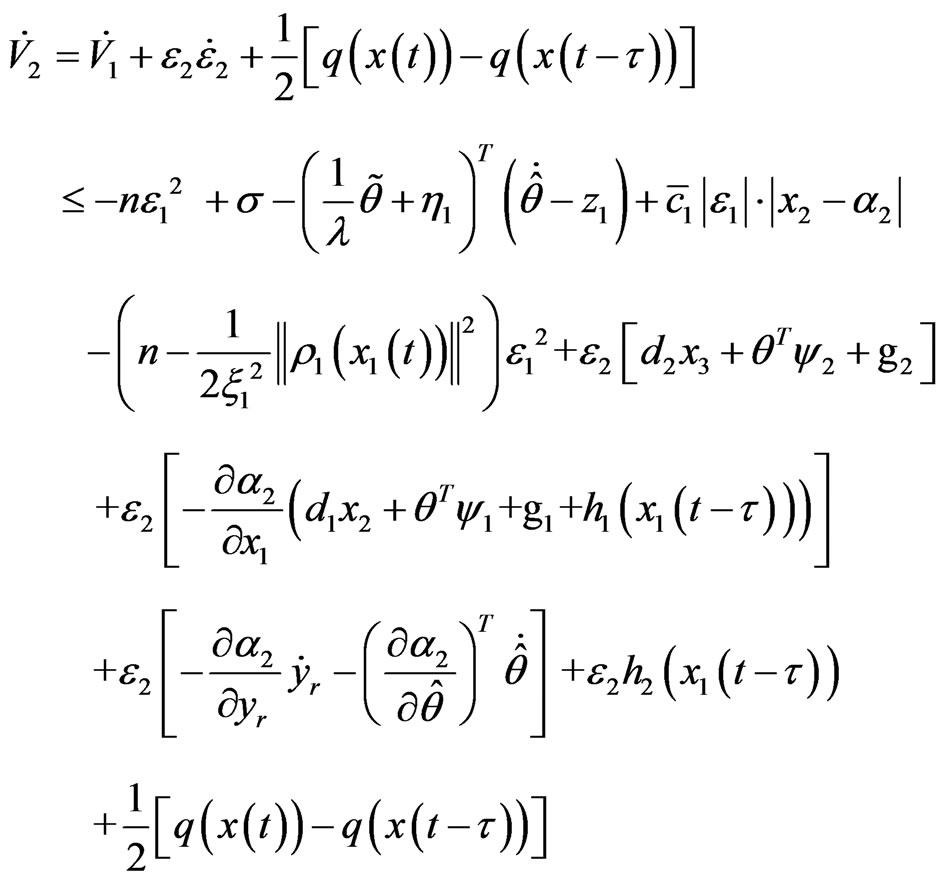
Let

Then we have
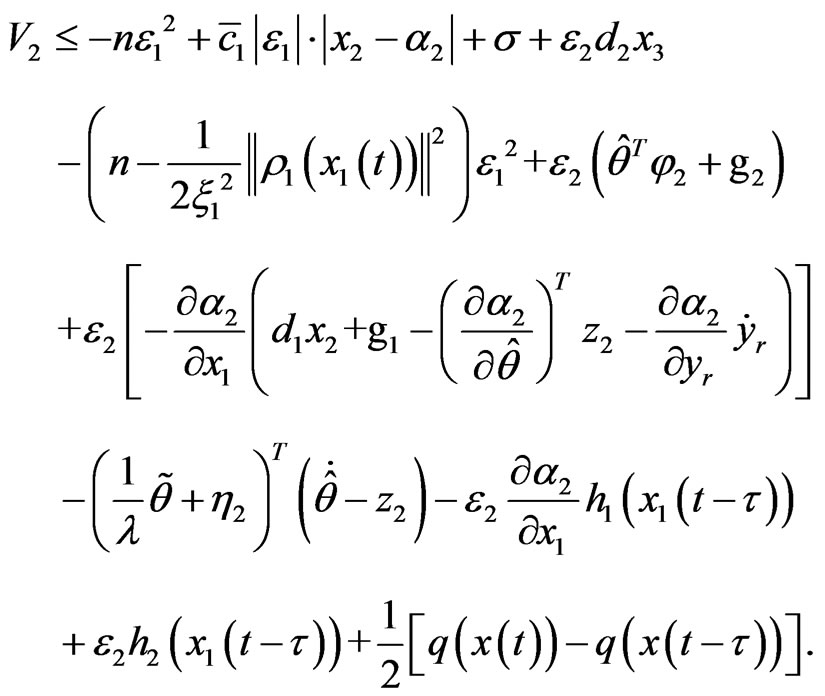 (6)
(6)
There exists a non-negative smooth function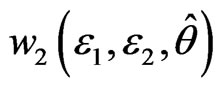 , satisfies
, satisfies

By Lemma 1, let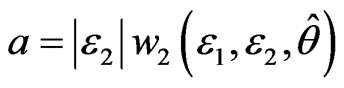 , b = σ so that there exists a smooth function
, b = σ so that there exists a smooth function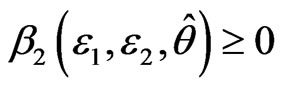 , satisfies
, satisfies
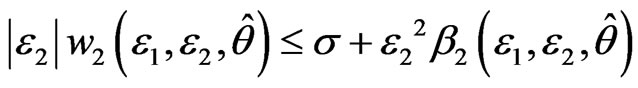 . (7)
. (7)
And because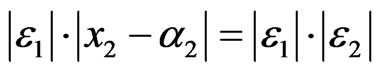 , combined with Lemma 1, there exists a smooth function
, combined with Lemma 1, there exists a smooth function 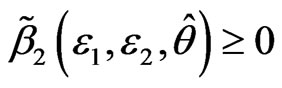 satisfies
satisfies
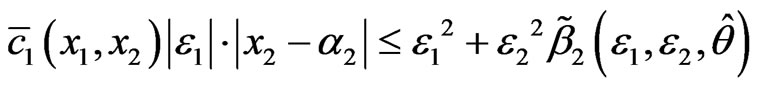 . (8)
. (8)
By using Young inequality, let constant ξ2 > 0, μ2 > 0, we have
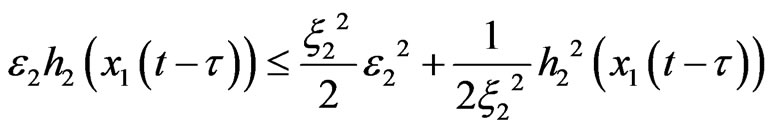
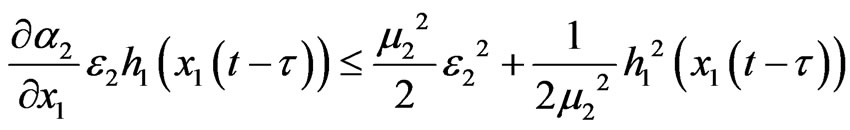
Select
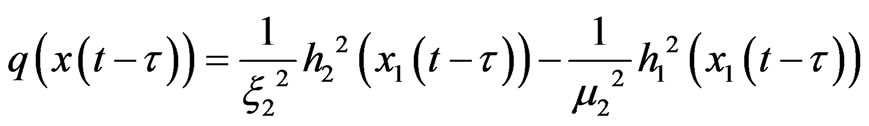
then we have

Then we have
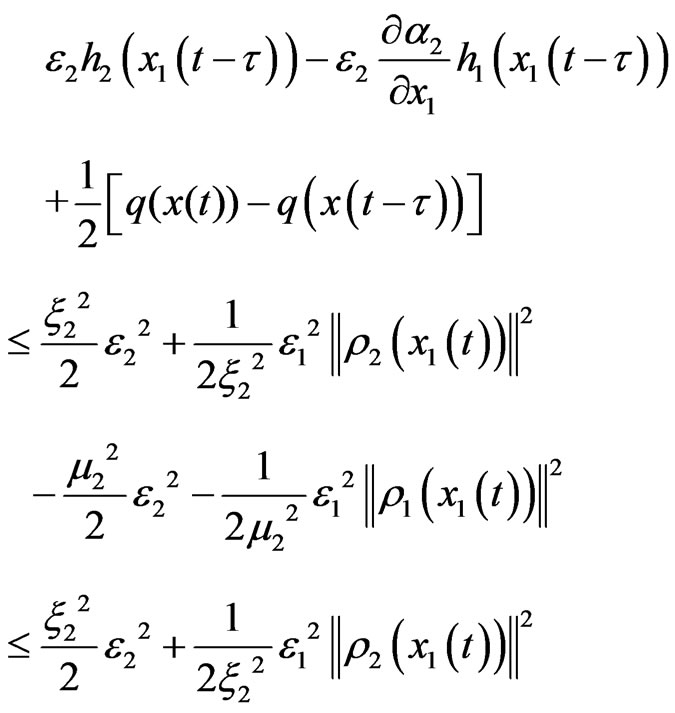 (9)
(9)
Substituting (7), (8), (9) into (6), we have
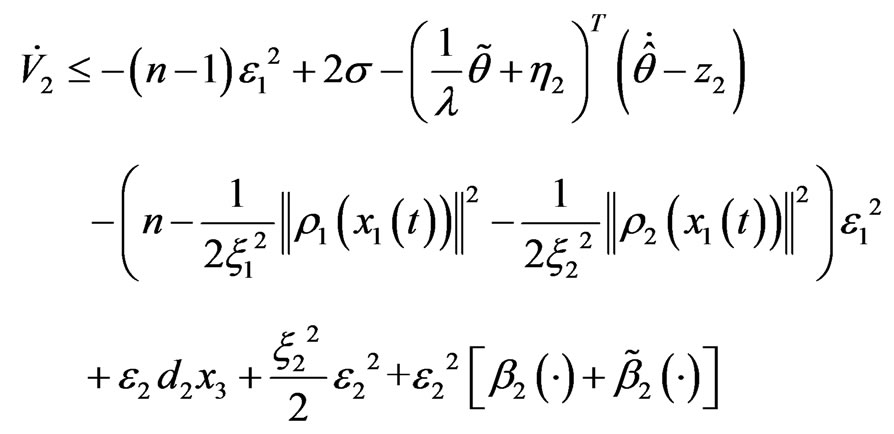
Designed virtual controller as

where f2(·) is a smooth function that is greater than zero.
By assumption 1, we have
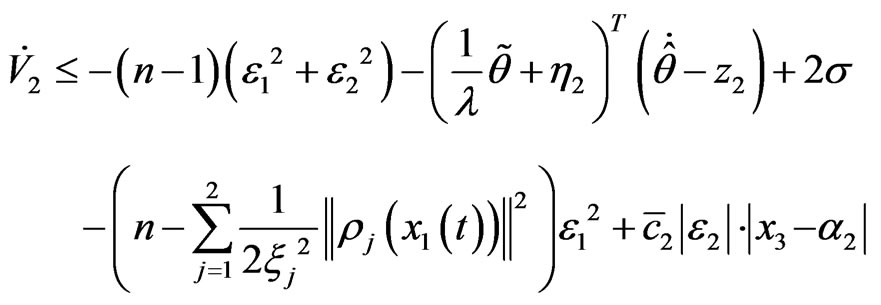
Step i After the recursive design step i-1, we can get a group of smooth virtual controller as
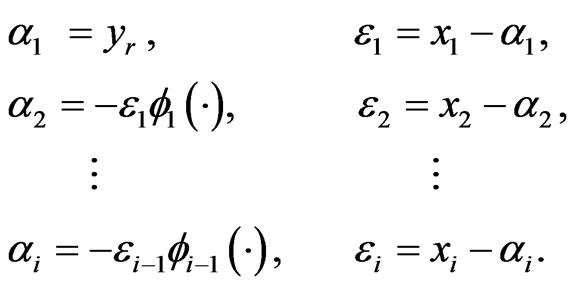
where smooth function fk(·) > 0, k = 1, ···, i – 1.
Constructed Lyapunov function as
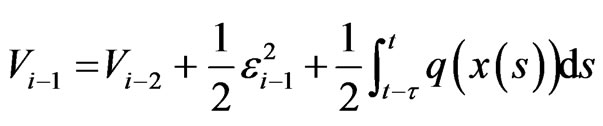
The derivative of Vi–1 as following
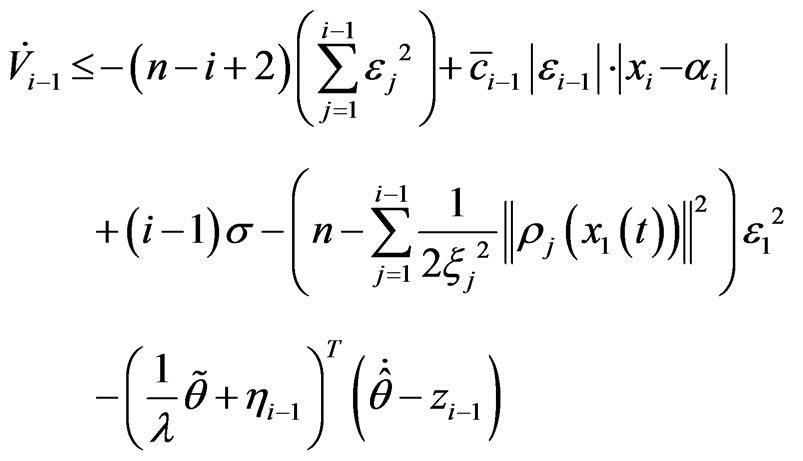 (10)
(10)
Similar to step 2, we can prove (10) is also established in the step i.
Constructed Lyapunov function as
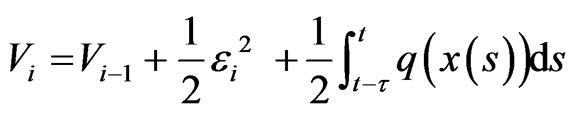
Its derivative is given by
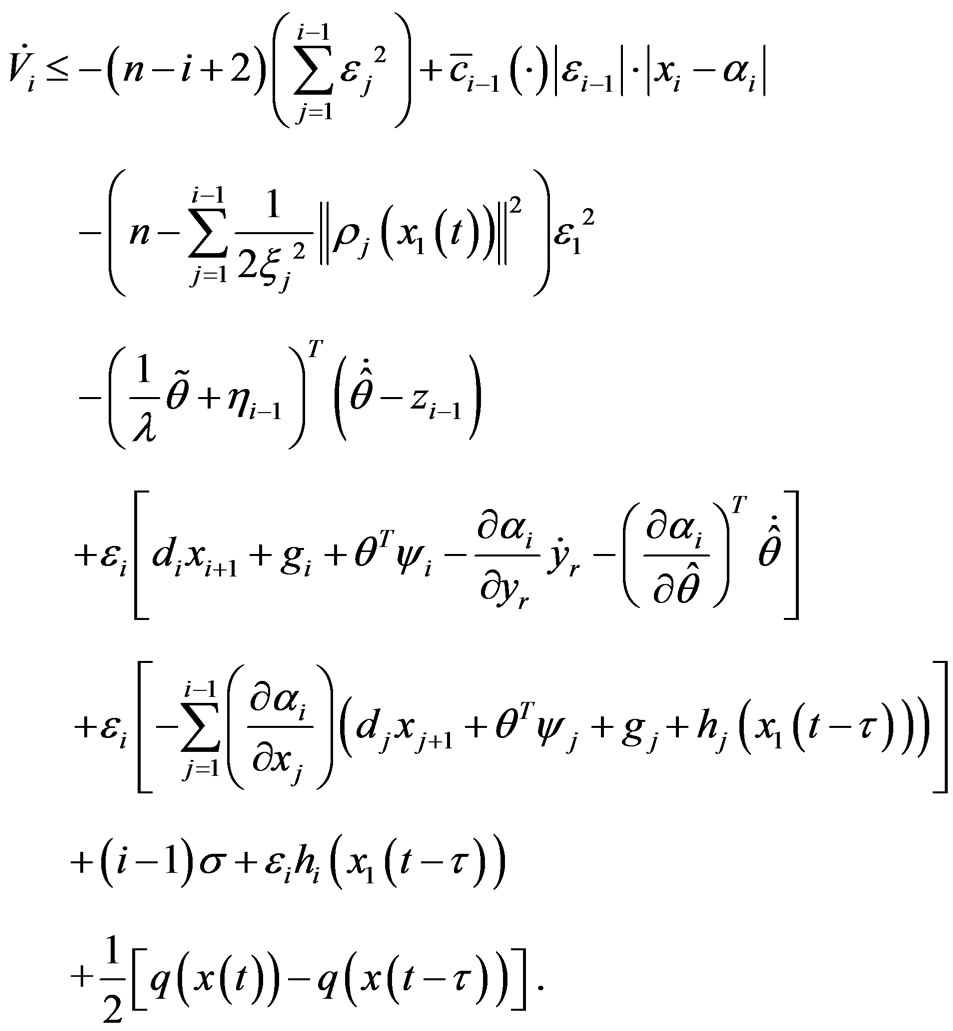
Let
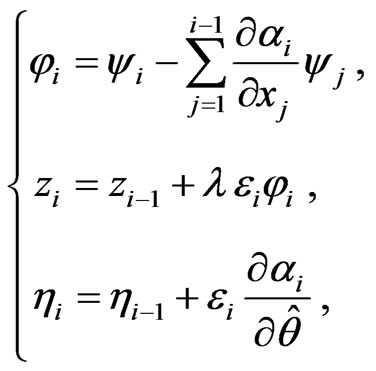
Then we have
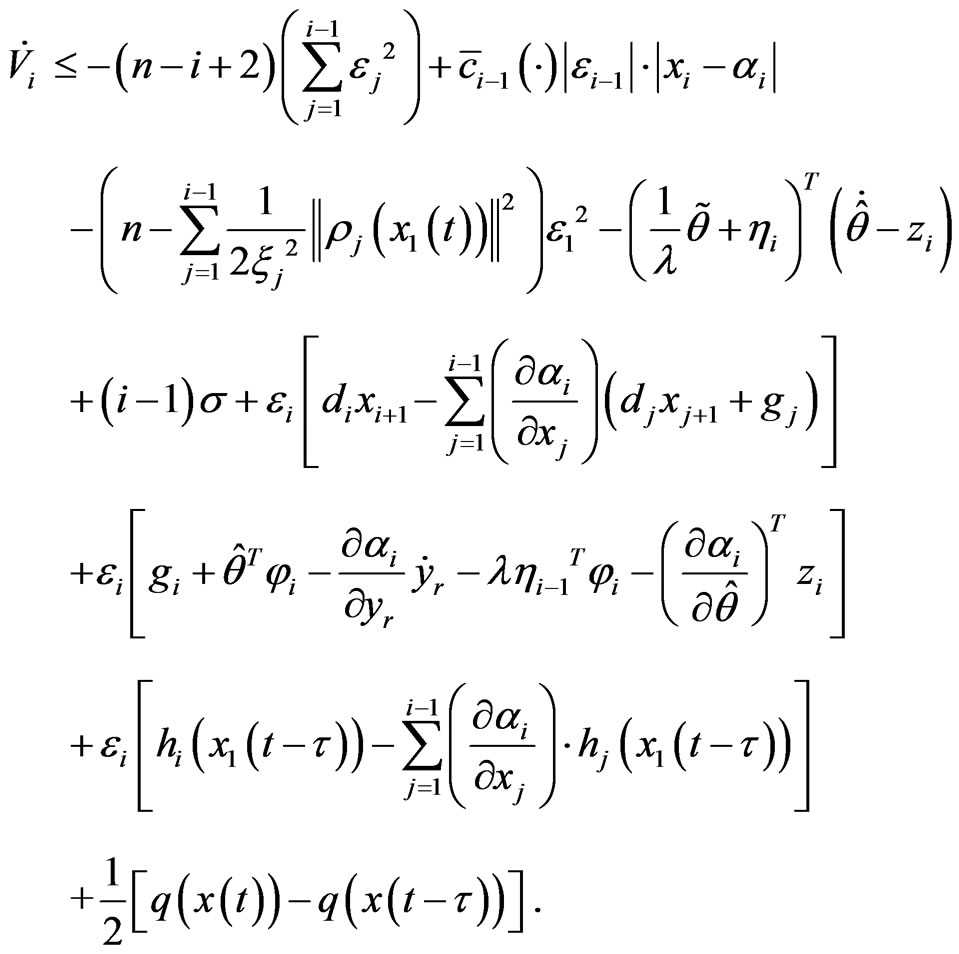 (11)
(11)
There exists a non-negative smooth function wi(·), satisfies
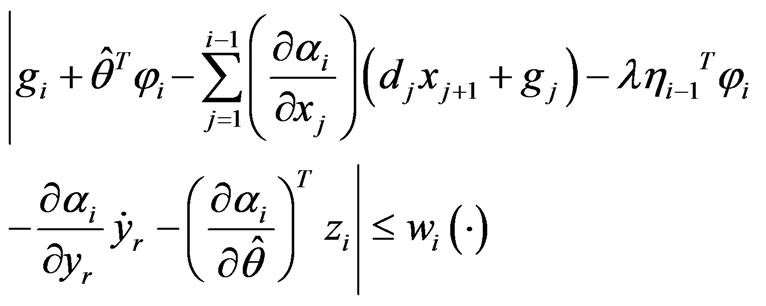
By the Lemma 1, there exists a smooth function βi(·) ≥ 0 satisfies
 (12)
(12)
Similar to step 2, there exists a smooth function 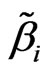 (·) ≥ 0 satisfies
(·) ≥ 0 satisfies
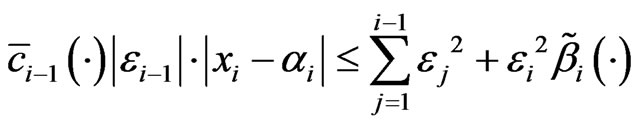 . (13)
. (13)
By using Young inequality, let constant ξi > 0, μi > 0, we have

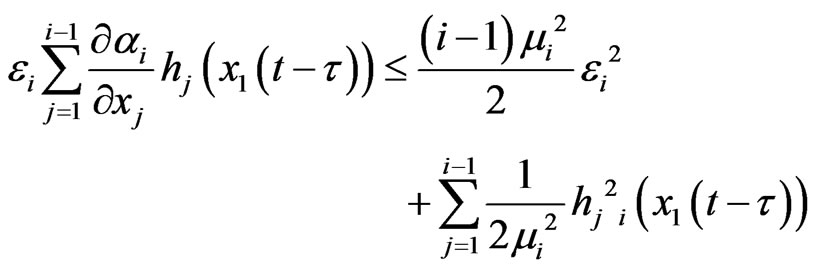
select
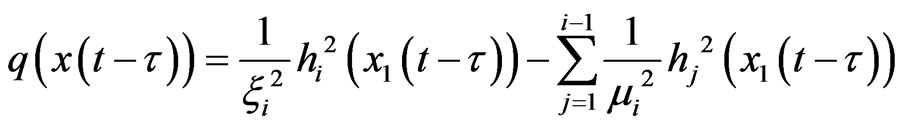
then we have
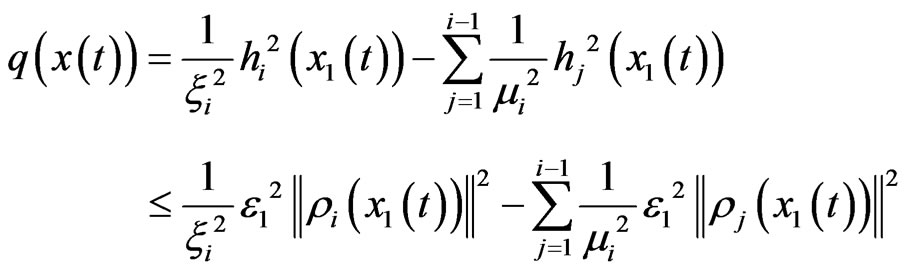
Then we have

Then we have

Designed virtual controller as
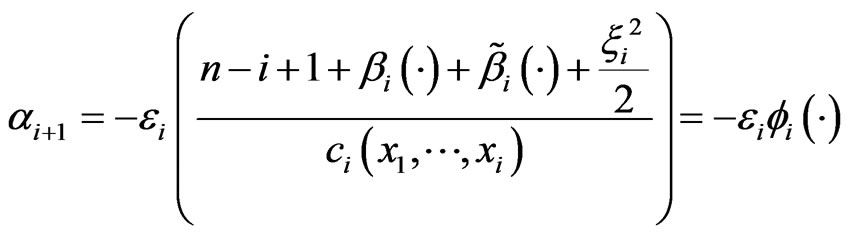
where fi(·) is a smooth function that is greater than zero.
By assumption 1, we have

Step n After repeated recurrence and proof, in the step n, constructed Lyapunov function as
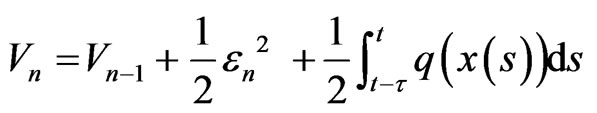
Its derivative is given by
 (14)
(14)
From (14), we can obtain adaptive control law u and parameter  following as
following as
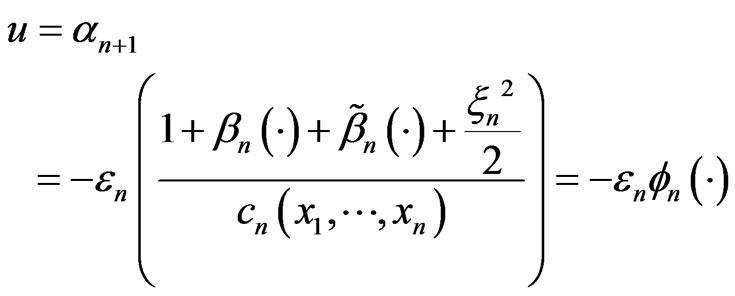 (15)
(15)
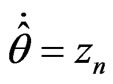 (16)
(16)
where fn(·) is a smooth function that is greater than zero.
Then, we have
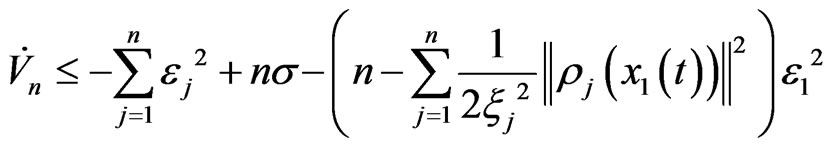 .
.
When n is large enough, then we have
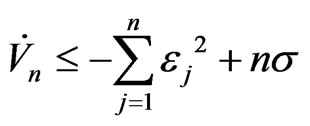
Select 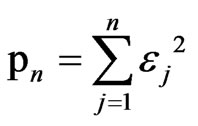 then we have
then we have 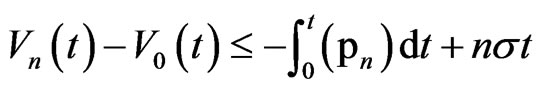 .
.
Therefore, we get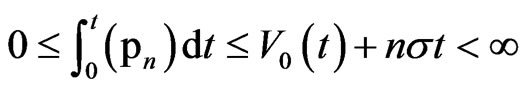 .
.
By Barbalat lemma, we get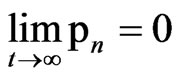 , and then we have
, and then we have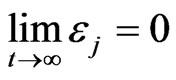 , j = 1, ···, n. So that we get
, j = 1, ···, n. So that we get .
.
So that the entire design procedure is reasonable.
Theorem 1 Considering closed-loop systems (1), under assumption and Lemma, there exist a state feedback control law u and control law parameter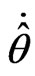 . The closedloop system is bounded for all allowable uncertainties and the output tracking error converges to a relatively small area, which satisfies
. The closedloop system is bounded for all allowable uncertainties and the output tracking error converges to a relatively small area, which satisfies
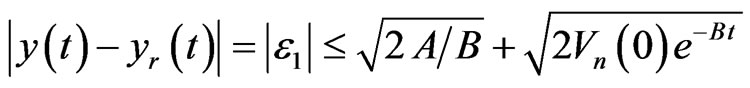 .
.
Proof
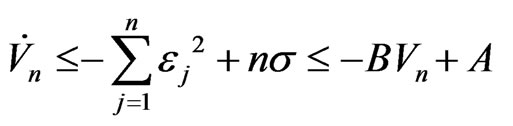
where
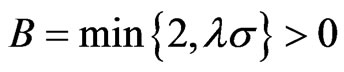

By Gronwall inequality, we have

And because
 So that we have
So that we have
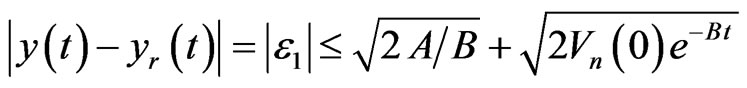 .
.
In summary, for any real number ε0 > 0, in limited time T > 0, the closed-loop system satisfies
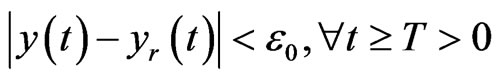 .
.
4. Simulation Example
In order to show the effectiveness of the design scheme, we choose the nonlinear network control system with parameter uncertainties and time-delay as following:
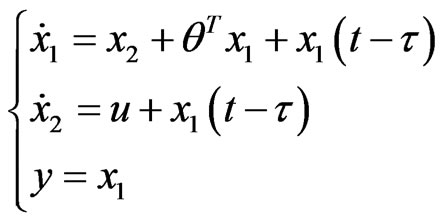 (17)
(17)
In the simulation, for the closed-loop system (17), we choose the reference signal yr(t) = sint, time-delay τ = 0.01s, θ = 0.2, ξ1 = 1, ξ2 = 2, σ = 0.02, λ = 1, the initial conditions x1(0) = 1, x2(0) = 0.5, 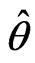 (0) = 0.1, According to (15) and (16), the control law u and the parameter of control law
(0) = 0.1, According to (15) and (16), the control law u and the parameter of control law 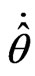 following as
following as

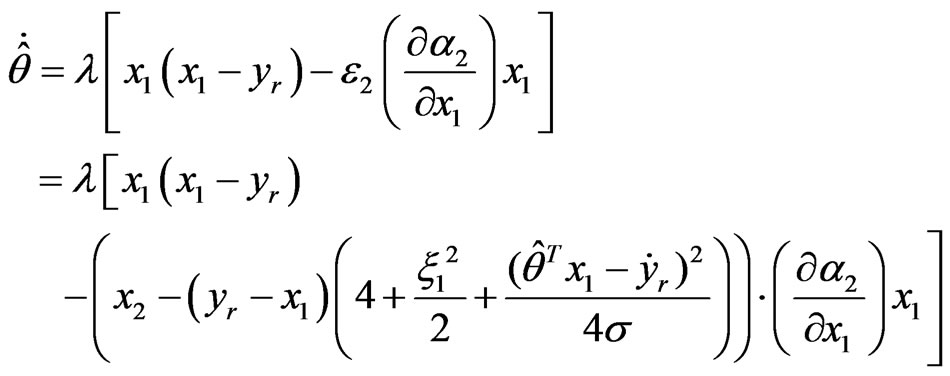
The simulation results are shown as in Figures 1 and 2. It can be observed that the output of closed-loop system can track the reference signal well, and the tracking error converges to a small neighborhood of the origin. Therefore the robust adaptive controller is effective.
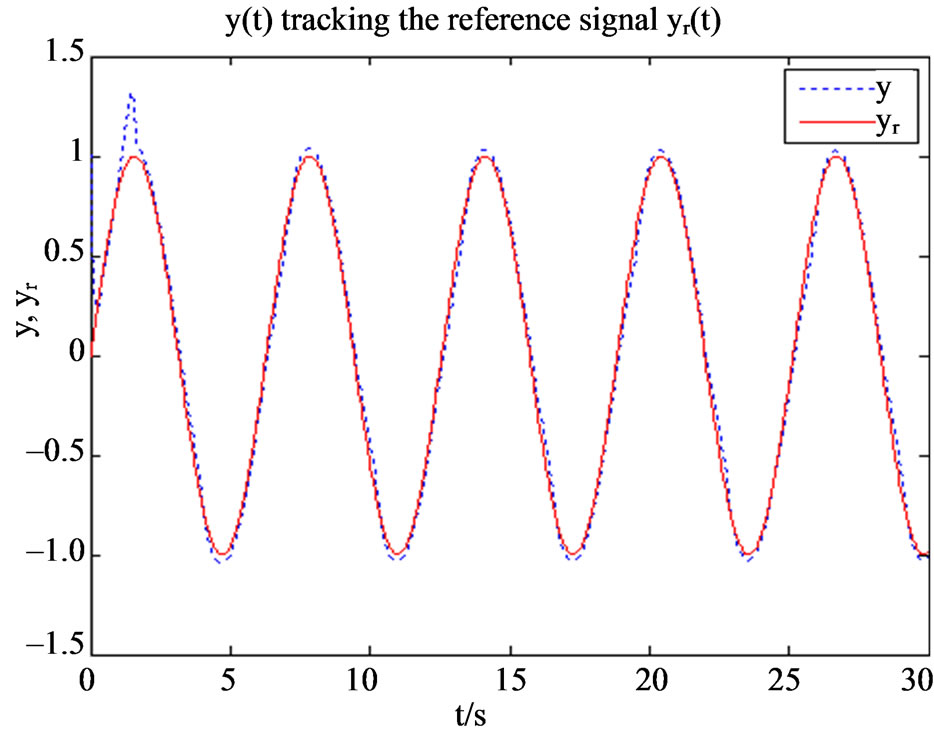
Figure 1. Output y(t) and reference signal yr(t).
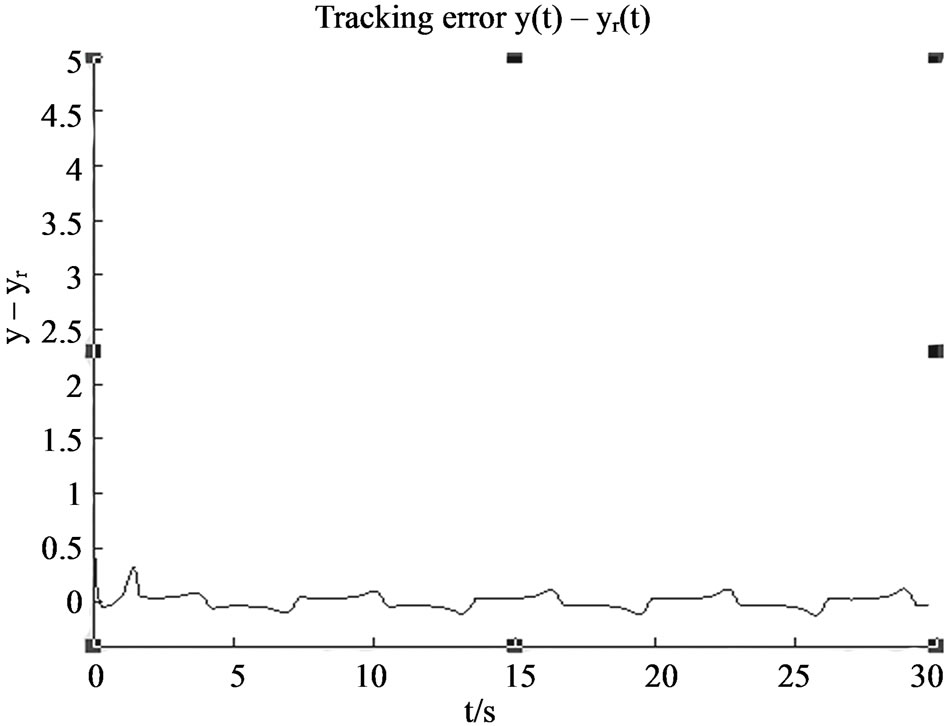
Figure 2. Output tracking error y(t) – yr(t).
5. Conclusion
By using the backstepping method, we design a controller for nonlinear network system with parameter uncertainties and time-delay. Through theoretical analysis, it is shown that the designed robust adaptive output tracking controller is feasible. The simulation results further expressed the effectiveness of the scheme.
6. Acknowledgements
This work was supported in part by the Natural Science Foundation of Chongqing (CSTC) under Grant No. 2009BB3280, and the National Natural Science Foundation of China under Grant No. 60873200.
REFERENCES
- J. P. Hespanha, P. Naghahtabrizi and Y. G. Xu, “A Survey of Recent Results in Networked Control Systems,” Proceedings of the IEEE, Vol. 95, No. 1, 2007, pp. 138- 162. doi:10.1109/JPROC.2006.887288
- L. A. Montestruque and E. J. Antsaklis, “On the ModelBased Control of Networked Systems,” Automatica, Vol. 39, No. 10, 2003, pp. 1837-1843. doi:10.1016/S0005-1098(03)00186-9
- G. C. Walsh, Y. Hong and L. G. Bushnell, “Stability Analysis of Networked Control Systems,” IEEE Transactions on Control Systems Technology, Vol. 10, No. 3, 2002, pp. 438-446. doi:10.1109/87.998034
- A. V. Savkin, “Analysis and Synthesis of Networked Control Systems: Topologicall Entropy, Observability, Robustness and Optimal Control,” Automatica, Vol. 41, No. 1, 2006, pp. 51-62. doi:10.1016/j.automatica.2005.08.021
- D. Yue, Q. L. Han and C. Peng, “State Feedback Controller Design of Networked Control Systems,” IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 51, No. 11, 2004, pp. 640-644. doi:10.1109/TCSII.2004.836043
- P. V. Zhivoglyadov and R. H. Middleton, “Networked Control Design for Linear Systems,” Automatica, Vol. 39, No. 4, 2003, pp. 743-750. doi:10.1016/S0005-1098(02)00306-0
- T. Yodyium and M. Y. Chow, “Control Methodologies in Networked Control Systems,” Control Engineering Practice, Vol. 11, No. 10, 2003, pp. 1099-1111. doi:10.1016/S0967-0661(03)00036-4
- W. Zhang, M. S. Branicky and S. M. Phillips, “Stability of Networked Control Systems,” IEEE Control Systems Magazine, Vol. 21, No. 1, 2001, pp. 84-99. doi:10.1109/37.898794
- H. S. Park, Y. H. Kim, D. S. Kim and W. H. Kwon, “A Scheduling Method for Network Based Control Systems,” IEEE Transactions on Control Systems Technology, Vol. 10, No. 3, 2002, pp. 318-330. doi:10.1109/87.998012
- D. S. Kim, Y. S. Lee, W. H. Kwon and H. S. Park, “Maximum Allowable Delay Bounds of Networked Control Systems,” Control Engineering Practice, Vol. 11, No. 11, 2003, pp. 1301-1313. doi:10.1016/S0967-0661(02)00238-1
- D. Liberzon and J. P. Hespanha, “Stabilization of Nonlinear Systems with Limited Information Feedback,” IEEE Transaction on Automatic Control, Vol. 50, No. 6, 2005, pp. 910-915. doi:10.1109/TAC.2005.849258
- D. Yue, Q. Han and J. Lam, “Network-Based Robust
 Control of Systems with Uncertainty,” Automatica, Vol. 41, No. 6, 2005, pp. 999-1007. doi:10.1016/j.automatica.2004.12.011
Control of Systems with Uncertainty,” Automatica, Vol. 41, No. 6, 2005, pp. 999-1007. doi:10.1016/j.automatica.2004.12.011 - L. Wei and R. Pongvuthithum, “Nonsmooth Adaptive Stabilization of Cascaded Systems with Nonlinear Parameterization via Partial-State Feedback,” IEEE Transaction on Automatic Control, Vol. 48, No. 10, 2003, pp. 1809- 1816. doi:10.1109/TAC.2003.817932
- Z. Y. Sun and Y. G. Liu, “State-Feedback Adaptive Stabilizing Control Design for a Class of High-Order Nonlinear Systems with Unknown Control Coefficients,” Journal of Systems Science and Complexity, Vol. 20, No. 10, 2007, pp. 350-361. doi:10.1007/s11424-007-9030-5
- Z. Y. Sun and Y. G. Liu, “Adaptive Stabilization for a Large Class of High-Order Uncertain Nonlinear Systems,” International Journal of Control, Vol. 82, No. 7, 2009, pp. 1275-1287. doi:10.1080/00207170802549529
- Z. Y. Sun, Y. G. Liu and Z. G. Liu, “An Adaptive Controller for a Class of High-Order Nonlinear Systems with Unknown Control Coefficients,” Proceedings of the 30th Chinese Control Conference, Yantai, 22-24 July 2011, pp. 266-271.
- N. B. He, C. S. Jiang and Q. Gao, “Adaptive Backstepping Control for a Class of Nonlinear Systems,” 3rd International Conference on Measuring Technology and Mechatronics Automation, Shanghai, 6-7 January 2011, pp. 322-325.
- N. B. He, C. S. Jiang and Q. Gao, “Robust Adaptive Backstepping Control of Nonlinear Systems with Uncertainty,” Journal of Applied Sciences Electronics and Information Engineering, Vol. 26, No. 6, 2008, pp. 650- 654.

