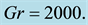Open Journal of Fluid Dynamics
Vol.05 No.03(2015), Article ID:59944,17 pages
10.4236/ojfd.2015.53026
Time-Dependent Flow with Convective Heat Transfer through a Curved Square Duct with Large Pressure Gradient
Rabindra Nath Mondal1*, Md. Nurul Amin Helal2, Poly Rani Shaha1, Nayan Kumar Poddar1
1Department of Mathematics, Jagannath University, Dhaka, Bangladesh
2Additional Director (Education), Training Directorate, BGB Head Quarter, Pilkhana, Dhaka, Bangladesh
Email: *rnmondal71@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 22 September 2015; published 25 September 2015
ABSTRACT
A numerical study is presented for the fully developed two-dimensional laminar flow of viscous incompressible fluid through a curved square duct for the constant curvature δ = 0.1. In this paper, a spectral-based computational algorithm is employed as the principal tool for the simulations, while a Chebyshev polynomial and collocation method as secondary tools. Numerical calculations are carried out over a wide range of the pressure gradient parameter, the Dean number, 100 ≤ Dn ≤ 3000 for the Grashof number, Gr, ranging from 100 to 2000. The outer wall of the duct is treated heated while the inner wall cooled, the top and bottom walls being adiabatic. The main concern of the present study is to find out the unsteady flow behavior i.e. whether the unsteady flow is steady-state, periodic, multi-periodic or chaotic, if Dn or Gr is increased. It is found that the un- steady flow is periodic for Dn = 1000 at Gr = 100 and 500 and at Dn = 2000, Gr = 2000 but steady-state otherwise. It is also found that for large values of Dn, for example Dn = 3000, the unsteady flow undergoes in the scenario “periodic®chaotic®periodic”, if Gr is increased. Typical contours of secondary flow patterns and temperature profiles are also obtained, and it is found that the unsteady flow consists of single-, two-, three- and four-vortex solutions. The present study also shows that there is a strong interaction between the heating-induced buoyancy force and the centrifugal force in a curved square passage that stimulates fluid mixing and consequently en- hance heat transfer in the fluid.
Keywords:
Curved Square Duct, Secondary Flow, Time-Evolution, Periodic Solution, Chaos

1. Introduction
Fluid flow and heat transfer in curved ducts have been studied for a long time because of their fundamental importance in engineering and industrial applications. Today, the flows in curved non-circular ducts are of increasing importance in micro-fluidics, where lithographic methods typically produce channels of square or rectangular cross-section. These channels are extensively used in many engineering applications, such as in turbo-machinery, refrigeration, air conditioning systems, heat exchangers, rocket engine, internal combustion engines and blade-to-blade passages in modern gas turbines. In a curved duct, centrifugal forces are developed in the flow due to channel curvature causing a counter rotating vortex motion applied on the axial flow through the channel. This creates characteristics spiraling fluid flow in the curved passage known as secondary flow. At a certain critical flow condition and beyond, additional pairs of counter rotating vortices appear on the outer concave wall of curved fluid passages which are known as Dean vortices, in recognition of the pioneering work in this field by Dean [1] . After that, many theoretical and experimental investigations have been done; for instance, the articles by Berger et al. [2] , Nandakumar and Masliyah [3] , and Ito [4] may be referenced.
One of the interesting phenomena of the flow through a curved duct is the bifurcation of the flow because generally there exist many steady solutions due to channel curvature. Studies of the flow through a curved duct have been made, experimentally or numerically, for various shapes of the cross section by many authors. However, an extensive treatment of the bifurcation structure of the flow through a curved duct of rectangular cross section was presented by Winters [5] , Daskopoulos and Lenhoff [6] and Mondal [7] .
Unsteady flows by time evolution calculation of curved duct flows was first initiated by Yanase and Nishiyama [8] for a rectangular cross section. In that study they investigated unsteady solutions for the case where dual solutions exist. The time-dependent behavior of the flow in a curved rectangular duct of large aspect ratio was investigated, in detail, by Yanase et al. [9] numerically. They performed time-evolution calculations of the unsteady solutions with and without symmetry condition and found that periodic oscillations appear with symmetry condition while aperiodic time variation without symmetry condition. Wang and Yang [10] [11] performed numerical as well as experimental investigation on fully developed periodic oscillation in a curved square duct. Flow visualization in the range of Dean numbers from 50 to 500 was carried out in their experiment. Recently, Yanase et al. [12] performed numerical investigation of isothermal and non-isothermal flows through a curved rectangular duct and addressed the time-dependent behavior of the unsteady solutions. In the succeeding paper, Yanase et al. [13] extended their work for moderate Grashof numbers and studied the effects of secon-dary flows on convective heat transfer. Recently, Mondal et al. [14] [15] performed numerical prediction of the unsteady solutions by time-evolution calculations for the flow through a curved square duct and discussed the transitional behavior of the unsteady solutions.
One of the most important applications of curved duct flow is to enhance the thermal exchange between two sidewalls, because it is possible that the secondary flow may convey heat and then increases heat flux between two sidewalls. Chandratilleke and Nursubyakto [16] presented numerical calculations to describe the secondary flow characteristics in the flow through curved ducts of aspect ratios ranging from 1 to 8 that were heated on the outer wall, where they studied for small Dean numbers and compared the numerical results with their experimental data. Yanase et al. [13] studied time-dependent behavior of the unsteady solutions for curved rectangular duct flow and showed that secondary flows enhance heat transfer in the flow. Mondal et al. [17] performed numerical prediction of the unsteady solutions by time-evolution calculations of the thermal flow through a curved square duct and studied convective heat transfer in the flow. Recently Norouzi et al. [18] [19] investigated fully developed flow and heat transfer of viscoelastic materials in curved square ducts under constant heat flux. Very recently, Chandratilleke and Narayanaswamy [20] numerically studied vortex structure-based analysis of laminar flow and thermal characteristics in curved square and rectangular ducts. To the best of the authors’ knowledge, however, there has not yet been done any substantial work studying the transitional behavior of the unsteady solutions for thermal flows through a curved square duct for combined effects of large Grashof number and large Dean number, which has very practical applications in fluids engineering, for example, in internal combustion engine, gas turbines etc. Thus from the scientific as well as engineering point of view it is quite interesting to study the unsteady flow behavior in the presence of strong buoyancy and centrifugal forces. Keeping this issue in mind, in this paper, a comprehensive numerical study is presented for fully developed two-dimen- sional (2D) flow of viscous incompressible fluid through a curved square duct and studied effects of secondary flows on convective heat transfer in the flow.
2. Mathematical Formulations
Consider an incompressible viscous fluid streaming through a curved duct with square cross section whose width or height is 2d. The coordinate system is shown in Figure 1. It is assumed that the temperature of the outer wall is 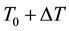 and that of the inner wall is
and that of the inner wall is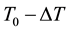 , where
, where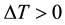 . The x, y, and z axes are taken to be in the horizontal, vertical, and axial directions, respectively. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient G along the center-line of the duct, i.e. the main flow in the axial direction as shown in Figure 1. The variables are non-dimensionalized by using the representative length d and the representative velocity
. The x, y, and z axes are taken to be in the horizontal, vertical, and axial directions, respectively. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient G along the center-line of the duct, i.e. the main flow in the axial direction as shown in Figure 1. The variables are non-dimensionalized by using the representative length d and the representative velocity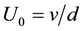 .
.
We introduce the non-dimensional variables defined as
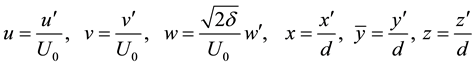
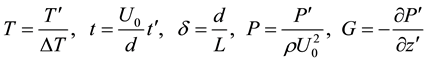 ,
,
where, u, v and w are the non-dimensional velocity components in the x, y and z directions, respectively; t is the non-dimensional time, P the non-dimensional pressure, 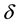 the non-dimensional curvature, and temperature is non-dimensionalized by
the non-dimensional curvature, and temperature is non-dimensionalized by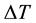 . Henceforth, all the variables are nondimensionalized if not specified. The stream function
. Henceforth, all the variables are nondimensionalized if not specified. The stream function 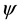 is introduced in the x- and y-directions as
is introduced in the x- and y-directions as
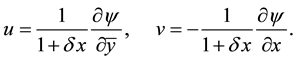 (1)
(1)
Then the basic equations for 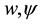 and
and 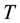 are derived from the Navier-Stokes equations and the energy equation under the Boussinesq approximation as,
are derived from the Navier-Stokes equations and the energy equation under the Boussinesq approximation as,
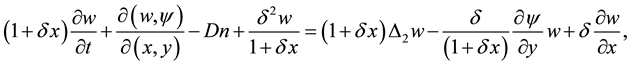 (2)
(2)
Figure 1. Coordinate system of the curved square duct.
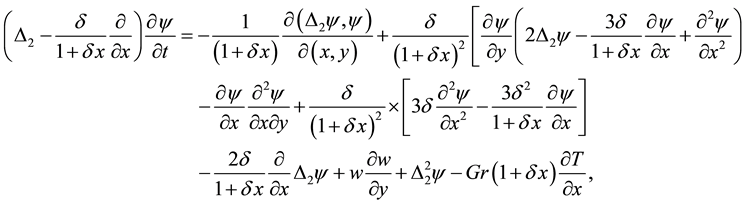 (3)
(3)
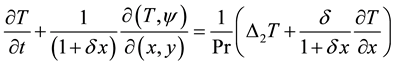 (4)
(4)
where,

The Dean number Dn, the Grashof number Gr, and the Prandtl number Pr, which appear in Equations (2) to (4) are defined as

The rigid boundary conditions for 

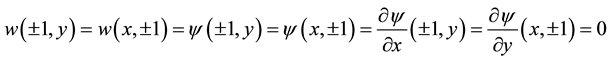
and the temperature 

In the present study, Dn and Gr vary while Pr and 
3. Numerical Calculations
3.1. Method of Numerical Calculation
In order to solve the Equations (2) to (4) numerically the spectral method is used. This is the method which is thought to be the best numerical method to solve the Navier-Stokes equations as well as the energy equation (Gottlieb and Orazag, [21] ). By this method the variables are expanded in a series of functions consisting of the Chebyshev polynomials. That is, the expansion functions

where 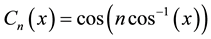
are expanded in terms of 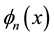


where 

3.2. Resistance Coefficient
The resistant coefficient 

where, quantities with an asterisk (*) denote dimensional ones, 

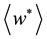
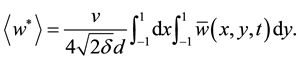
Since
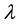

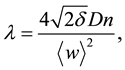
where, 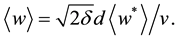
4. Results and Discussion
4.1. Time Evolution of the Unsteady Solutions
Time evolution of the resistance coefficient l are performed for 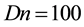
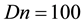
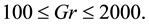
Figure 2. (a) Time-dependent flow for 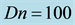



the contours for the stream lines of the secondary flow patterns 
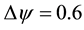
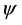
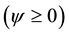

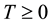
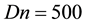
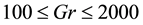
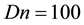
Then, we investigated time-dependent solutions of l for 



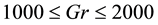


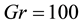
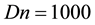

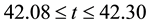
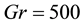

Figure 3. (a) Time-dependent flow for 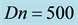



Figure 4. (a) Time-dependent flow for 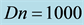

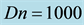
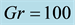
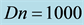
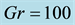
asymmetric two-vortex solution.
We then performed time evolution of l for Dn = 1500 and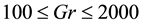
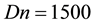

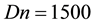
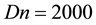




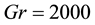



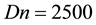
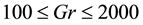



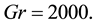
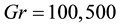
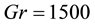
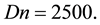






Figure 5. (a) Time-dependent flow for 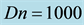
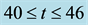
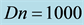
flows are asymmetric two-vortex solution.
Finally, the results of the time-dependent solutions for 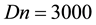

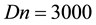

and 


the time-dependent flow creates multiple orbits, which suggests that the flow is multi-periodic. Typical contours
Figure 6. (a) Time-dependent flow for 



of secondary flow patterns and temperature profiles are shown in Figure 10(d), and it is found that the flow oscillates between asymmetric two-vortex solutions. Then we explicitly show the result of the time-dependent flow for 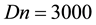

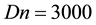

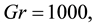
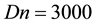

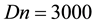

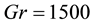

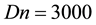
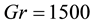
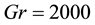
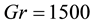
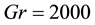

Figure 7. (a) Time-dependent flow for 

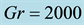

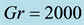
Figure 8. (a) Time-dependent flow for 

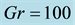
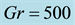
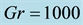
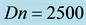
Figure 9. (a) Time-dependent flow for 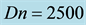
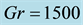
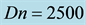

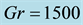
Figure 10. (a) Time-dependent flow for 

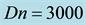

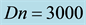
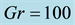
Figure 11. (a) Time-dependent flow for 
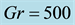
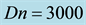

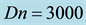
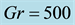
Figure 12. (a) Time-dependent flow for 


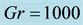
Figure 12. (c) Secondary flow patterns (top) and temperature profiles (bottom) for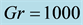
Figure 13. (a) Time-dependent flow for 
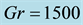
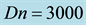

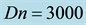
Figure 14. (a) Time-dependent flow for 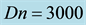
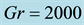


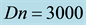
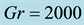
4.2. Phase Diagram in the Dn-Gr Plane
Finally, the distribution of the time-dependent solutions, obtained by the time evolution calculations of the curved square duct flows, is shown in Figure 15 in the Dean number versus Grashof number (Dn-Gr) plane for 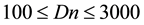
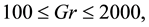


5. Conclusion
A numerical study is presented for the time-dependent solutions of the flow through a curved square duct of constant curvature

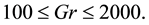
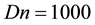

Figure 15. Distribution of the time-dependent solutions in the Dean number vs. Grashof number (Dn-Gr) plane for 




are also obtained, and it is found that periodic or multi-periodic solution oscillates between asymmetric two-, and four-vortex solutions, while for chaotic solution, there exist only asymmetric two-vortex solution. The temperature distribution is consistent with the secondary vortices and it is found that the temperature distribution occurs significantly from the heated wall to the fluid as the secondary flow becomes stronger. The present study also shows that there is a strong interaction between the heating-induced buoyancy force and the centrifugal force in the curved passage which stimulates fluid mixing and thus results in thermal enhancement in the flow.
Cite this paper
Rabindra NathMondal,Poly RaniShaha,Md. Nurul AminHelal,Nayan KumarPoddar, (2015) Time-Dependent Flow with Convective Heat Transfer through a Curved Square Duct with Large Pressure Gradient. Open Journal of Fluid Dynamics,05,238-255. doi: 10.4236/ojfd.2015.53026
References
- 1. Dean, W.R. (1927) Note on the Motion of Fluid in a Curved Pipe. Philosophical Magazine, 4, 208-223.
http://dx.doi.org/10.1080/14786440708564324 - 2. Berger, S.A., Talbot, L. and Yao, L.S. (1983) Flow in Curved Pipes. Annual Review of Fluid Mechanics, 35, 461-512.
http://dx.doi.org/10.1146/annurev.fl.15.010183.002333 - 3. Nandakumar, K. and Masliyah, J.H. (1986) Swirling Flow and Heat Transfer in Coiled and Twisted Pipes. Advances in Transport Process, 4, 49-112.
- 4. Ito, H. (1987) Flow in Curved Pipes. JSME International Journal, 30, 543-552.
- 5. Winters, K.H. (1987) A Bifurcation Study of Laminar Flow in a Curved Tube of Rectangular Cross-Section. Journal of Fluid Mechanics, 180, 343-369.
http://dx.doi.org/10.1017/S0022112087001848 - 6. Daskopoulos, P. and Lenhoff, A.M. (1989) Flow in Curved Ducts: Bifurcation Structure for Stationary Ducts. Journal of Fluid Mechanics, 203, 125-148.
http://dx.doi.org/10.1017/S0022112089001400 - 7. Mondal, R.N. (2006) Isothermal and Non-Isothermal Flows through Curved Duct with Square and Rectangular Cross-Section. Ph.D. Thesis, Department of Mechanical and Systems Engineering, Okayama University, Japan.
- 8. Yanase, S. and Nishiyama, K. (1988) On the Bifurcation of Laminar Flows through a Curved Rectangular Tube. Journal of the Physical Society of Japan, 57, 3790-3795.
http://dx.doi.org/10.1143/JPSJ.57.3790 - 9. Yanase, S., Kaga, Y. and Daikai, R. (2002) Laminar Flow through a Curved Rectangular Duct over a Wide Range of the Aspect Ratio. Fluid Dynamics Research, 31, 151-183.
http://dx.doi.org/10.1016/S0169-5983(02)00103-X - 10. Wang, L. and Yang, T. (2005) Periodic Oscillation in Curved Duct Flows. Physica D, 200, 296-302.
http://dx.doi.org/10.1016/j.physd.2004.11.003 - 11. Wang, L.Q. and Yang, T.L. (2004) Multiplicity and Stability of Convection in Curved Ducts: Review and Progress, Advances in Heat Transfer, 38, 203-256.
http://dx.doi.org/10.1016/s0065-2717(04)38004-4 - 12. Yanase, S., Mondal, R.N., Kaga, Y. and Yamamoto, K. (2005) Transition from Steady to Chaotic States of Isothermal and Non-Isothermal Flows through a Curved Rectangular Duct. Journal of the Physical Society of Japan, 74, 345-358.
http://dx.doi.org/10.1143/JPSJ.74.345 - 13. Yanase, S., Mondal, R.N. and Kaga, Y. (2005) Numerical Study of Non-Isothermal Flow with Convective Heat Transfer in a Curved Rectangular Duct. International Journal of Thermal Sciences, 44, 1047-1060.
http://dx.doi.org/10.1016/j.ijthermalsci.2005.03.013 - 14. Mondal, R.N., Kaga, Y., Hyakutake, T. and Yanase, S. (2007) Bifurcation Diagram for Two-Dimensional Steady Flow and Unsteady Solutions in a Curved Square Duct. Fluid Dynamics Research, 39, 413-446.
http://dx.doi.org/10.1016/j.fluiddyn.2006.10.001 - 15. Mondal, R.N., Uddin M.S. and Yanase, S. (2010) Numerical Prediction of Non-Isothermal Flow through a Curved Square Duct. International Journal of Fluid Mechanics Research, 37, 85-99.
http://dx.doi.org/10.1615/InterJFluidMechRes.v37.i1.60 - 16. Chandratilleke, T.T. and Nursubyakto, S. (2003) Numerical Prediction of Secondary Flow and Convective Heat Transfer in Externally Heated Curved Rectangular Ducts. International Journal of Thermal Sciences, 42, 187-198.
http://dx.doi.org/10.1016/S1290-0729(02)00018-2 - 17. Mondal, R.N., Kaga, Y., Hyakutake, T. and Yanase, S. (2006) Effects of Curvature and Convective Heat Transfer in Curved Square Duct Flows. Journal of Fluids Engineering, 128, 1013-1023.
http://dx.doi.org/10.1115/1.2236131 - 18. Norouzi, M., Kayhani, M.H., Nobari, M.R.H. and Karimi Demneh, M. (2009) Convective Heat Transfer of Viscoelastic Flow in a Curved Duct, World Academy of Science, Engineering and Technology, 32, 327-333.
- 19. Norouzi, M., Kayhani, M.H., Shu, C. and Nobari, M.R.H. (2010) Flow of Second-Order Fluid in a Curved Duct with Square Cross-Section. Journal of Non-Newtonian Fluid Mechanics, 165, 323-339.
http://dx.doi.org/10.1016/j.jnnfm.2010.01.007 - 20. Chandratilleke, T.T., Nadim, N. and Narayanaswamy, R. (2012) Vortex Structure-Based Analysis of Laminar Flow Behaviour and Thermal Characteristics in Curved Ducts. International Journal of Thermal Sciences, 59, 75-86.
http://dx.doi.org/10.1016/j.ijthermalsci.2012.04.014 - 21. Gottlieb, D. and Orazag, S.A. (1977) Numerical Analysis of Spectral Methods. Society for Industrial and Applied Mathematics, Philadelphia.
- 22. Ligrani, P.M. and Niver, R.D. (1988) Flow Visualization of Dean Vortices in a Curved Channel with 40 to 1 Aspect Ratio. Physics of Fluids, 31, 3605.
http://dx.doi.org/10.1063/1.866877
NOTES
*Corresponding author.