Received 8 March 2015; accepted 30 May 2015; published 2 June 2015

ABSTRACT

The incompressible viscous steady flow through a rotating curved pipe of circular cross-section with magnetic field is investigated numerically to examine the combined effects of rotation (Coriolis force), magnetic field and curvature (centrifugal force) on the flow. The curvature of the pipe has been assumed to be small, that is, the radius of the circle in which the central line of the pipe is coiled is large in comparison with the radius of the cross section. Spectral method is applied as a main tool for the numerical technique, where Fourier series, Chebyshev polynomials, Collocation methods, and Iteration method are used as secondary tools. The flow depends on the Taylor number (T_r), Dean Number (D_n), Magnetic Parameter (M) and the dimensionless curvature of the pipe δ. When T_r > 0, the rotation is in the direction so that the Coriolis force enforces the curvature effect. When T_r < 0, the rotation is in the direction so that the Coriolis force exhibits an opposite effect to that of the curvature. The calculations are carried out for −1500 ≤ T_r ≤ 1500, D_n ≥ 1000 (large Dean number), M ≥ 0 and δ = 0.01. Due to high magnetic field four-vortex solution is observed in a rotating curved pipe system. Visualization is attained with MAPLE software.

Keywords:

Curvature, Spectral Method, Taylor Number, Dean Number and Magnetic Parameter

1. Introduction

The flow through a curved pipe has attracted considerable attention not only because of its practical importance, but also because of the interesting physical properties under the action of the centrifugal force due to the curvature of the pipe. Curved pipe geometries are also in bio-fluid mechanics. It is widely used in the pipeline such as consumption in aircraft. All these important features occur as a result of the curvature of the pipe and the rotation. When the pipe is rotated about an axis normal to a plane containing the line, it originates Coriolis force, affecting the effect of the centrifugal force. Therefore, it reveals the most interesting features that expand the use of rotating curved pipe for industrial especially in chemical engineering and mechanical engineering.

All these interesting features drew the attention of a lot of scientist to different types of flows different types of ducts. Dean [1] [2] was the first author to formulate the problem mathematically. Here incompressible viscous fluid flow under constant pressure gradient force has been investigated and the flow is found to be depen-

dent on a parameter termed as Dean number D_n given by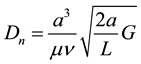; where, μ is the coefficient of vis-

cosity, 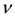is the kinematic viscosity, G is the pressure gradient force, L is the radius of curvature and a is the radius of the cross-section. This type of flow is called Dean flow. Adler [3] observed secondary-flow boundary layers on the two halves of the torus and inferred that the two boundary layers (on the upper and lower halves) collide at the innermost point of the cross-section, separate there, and form a re-entrant jet that moves outward through the core. Winters [4] studied the stability of dual solution regarding flow through a curved duct using a finite element method. Yanase et al. [5] studied the linear stability of the dual solution for flow through a curved duct on the assumptions of Dean approximation and the two-dimensionality of the flow.

The effects of the magnetic field on fluid flow have been studied primarily for straight pipes by Chang and Lundgren [6] , Shercliff [7] and Walker [8] . Shercliff [7] solved the problem of flow in circular pipes under transverse magnetic fields in an approximate manner for large Hartmann numbers assuming walls of zero and small conductivity. The effect of wall conductivity was also studied by Chang and Lundgren [6] . Walker [8] developed solutions to MHD flow equations by asymptotic analysis for circular straight ducts under strong transverse magnetic fields. The effects of Dean number and curvature in a curved pipe have been studied by Masud et al. [9] . Recently, Hoque et al. [10] -[12] considered the wide range of magnetic effects on a circular curved pipe to a wide range of curvature and Dean number.

But if the curved pipe rotates, in addition to centrifugal force the fluid experiences Coriolis force. The rotation is considered to be positive if it is in such a direction that the Coriolis force results a positive effect to that of the centrifugal force and this case is known as co-rotating case. Otherwise the rotation is considered to be negative and is known as counter rotating case. But when the fluid flows through a curved pipe, the particles experience centrifugal force which brings about the secondary flow. This was first noticed by Williams et al. [13] . They also found that the location of the maximum axial velocity was shifted towards the outer wall as an effect of the occurrence of secondary flow. Miyazaki [14] examined the solutions for co-rotating case. Ito and Motai [15] investigated both co-rotating and counter rotating cases. A reduction in the strength of the secondary flow and even a secondary flow reversal was observed for counter rotating case. At this time, the concept of bifurcation was not so rich. Later Daskopoulos and Lenhoff [16] showed the bifurcation study of the flow combined with curvature and rotation. Recently, Hoque et al. [17] analyzed the magneto hydrodynamic curved duct flow problem using spectral methods, motivated by applications in bioastronautics.

For a wide range of Dean number, the magnetic field, and the curvature, no work as regards the flow of curved pipe with the rotation has been made. In this regard, it is quite innovative to study the flow in a rotating curved pipe for a wide range of Dean number, magnetic field, and the curvature of understanding the behavior of the flow. In the present study, we apply a spectral collocation computation method (Beg et al. [18] ) to simulate viscous incompressible MHD flow in a rotating curved pipe system. A polynomial expansion is employed to obtain steady-state solutions. Fourier series and Chebyshev polynomials are used in circumferential and radial direction, respectively. The computations are shown to agree with previous studies but reveal more complex vortex patterns than previously reported. In particular, the combine effects of Taylor number, Dean number as well magnetic parameter are examined, for prescribed curvature. In this study, the magnetic field has been imposed along the center line of a rotating curved pipe.

2. Governing Equation

A curved pipe with magnetic field of uniform circular cross section has been considered. The pipe is rotated at a constant angular velocity about an axis passing through the center of curvature of the pipe and perpendicular to the plane containing the axis of the pipe. Now, consider the coordinate systems 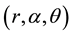as shown in the Figure 1. Where, O is the center of curvature, L is the radius of the pipe, a is the radius of the cross-section, is

the circumferential angle, θ is the axial variable and r is the radial variable. The non-dimensional velocity components along the radial, circumferential and axial direction are u', v', w' respectively. r' is non-dimensional radius, S' is the non-dimensional axial variable, δ is non-dimensional curvature and p' non-dimensional pressure.

Let us defined the following non-dimensional variables

;;;;;;.

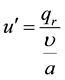We get following momentum equations,

Non-dimensional radial momentum equation:

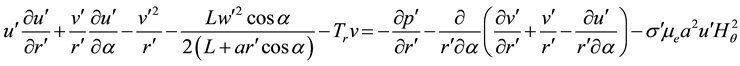. (1)

Non-dimensional circumferential momentum equation:

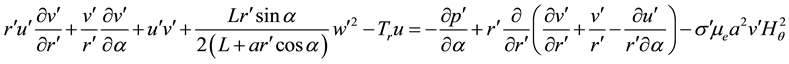. (2)

Non-dimensional axial momentum equation:

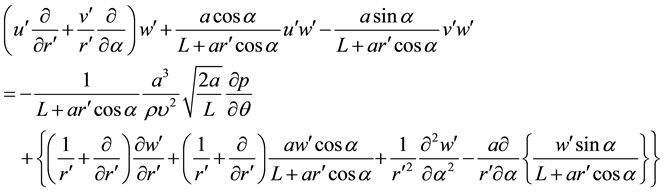(3)

and the non-dimensional continuity equation:

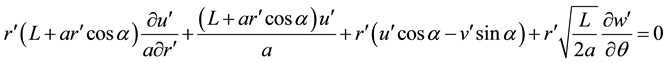. (4)

The other variables without primes are dimensional variables. Constant pressure gradient force is applied along the axial direction through the centre of cross section. With the help of the above dimensionless variables and the boundary conditions the equation of motion reduces to the following form:

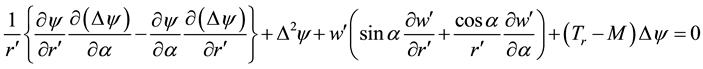(5)

and

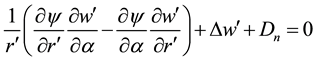. (6)

Here, 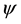is the stream function defined by, ,

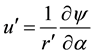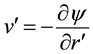
where,

, , ,

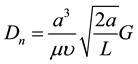and

3. Method of Numerical Calculation

The spectral method is applied in the numerical calculation. The Fourier series and Chebyshev polynomials are used in circumferential and radial directions respectively. Assuming that steady solution is symmetric with respect to the horizontal line of the cross-section, and are expanded as,

(7)

and

(8)

where N is the truncation number of the Fourier series. The collocation points are taken as

. (9)

The obtained algebraic non-linear equations are solved by an iteration method with under relaxation. Convergence of the solution assured by taking where subscripts p denotes the iteration number.

4. Results and Discussion

A rotating curved pipe with circular cross section has been considered which is rotating at a constant angular velocity. The main flow is forced by the magnetic field along the center line of the pipe and the corresponding Dean number. As the pipe is curved the flow is also subjected to centrifugal force, which results in a two-vortex secondary flow which remains symmetric about the horizontal line passing through the center of the cross section. If the effects of rotation and curvature are in the same direction, the rotation is called co-rotation in this case T_r is positive; if not, it is called counter rotation and in this case T_r is negative. Due to curved structure of the pipe magnetic force comes into action and various flow structures are found. In addition Coriolis force due to rotation makes it more complicated. In the present problem numerical calculations have been made at Dean number D_n = 2500 for two different magnetic parameter at curvature δ = 0.01.

The results have been shown through stream line, vector plots of the secondary flow and contour plots of the axial flow. The stream line, vector and contour plots of the flow development have been shown at different magnetic parameters and Taylor number for Dean number, D_n = 2500 at non-dimensional curvature δ = 0.01. The flow characteristics have been shown in Figure 2 and Figure 3. Contour plots of the axial flow, vector plots of the secondary flow and constant ψ-lines of the secondary flow have been shown at different T_r in the first,

second and third column respectively. The increment of the axial velocity is taken as Δw = 10 whereas the increment of the constant ψ-lines is Δψ = 0.50. The arrow indicates the direction of motion of the particle and the length of the arrow indicates the relative secondary velocity. In these figures the inner side of the cross section is to the left and the outer side is to the right.

In Figure 4 the change of flux with the change of Taylor number has been shown for M = 500 and 1000 respectively. The maximum flux has been found at negative T_r for all cases. In Figure 2 and Figure 3 two-vortex secondary flow patterns have been found, which are symmetric about the horizontal line passing through the centre of the cross section. In case of both figures, for δ = 0.01 and T_r > 0 the secondary flow gets stronger with the increase of T_r, as positive T_r enforces the effects of pressure gradient force.

But the axial flow decrease which results in a low flux. Again, for δ = 0.01 and T_r < 0 the Coriolis force oppose the effects of pressure gradient force and many interesting features are observed. The secondary flow gets weaker but the axial flow increase and as a result flux becomes higher. When −355.66 ≤ T_r ≤ 323.54, four-vor- tex secondary flow structures have been found for the Figure 2 and Figure 3. In this above domain flux increase drastically and at T_r = −350 highest flux occurs. After T_r goes below −350, flux again decrease and two-vortex flow pattern has been observed for magnetic parameter M = 500 and 1000.

Vector plots of the secondary flow have been shown in Figure 2 and Figure 3 for M = 500 and 1000 respectively. The secondary flow is set up just after entering the inlet due to the effect of centrifugal force. Most of the

particles get the radial velocity. Circumferential velocity is greater for the particles near the upper and lower boundary due to the friction with the wall. Also the velocity of the particles at the centre of the cross section is radially outward for the effect of the centrifugal force. As the flow downstream the secondary velocities of the particles near the centre of the cross section increase in the direction of the centrifugal force. At the same time, the particles near the upper and lower boundary experience high circumferential velocity in the direction opposite to the velocity of the particle at the core region. As a result two-vortex secondary flows is set up, which is symmetric about the horizontal plane passing through the centre of the cross section.

The contour plots of the axial velocity has been shown in Figure 2 and Figure 3 for D_n = 2500, M = 500 and 1000 respectively. As the flow enters the pipe boundary layer develops. Boundary layer near the inner wall develops faster than that at the outer wall. And with the development of the flow the strength of the axial flow is increased and is shifted towards the outer wall of the cross-section, which is effect of the centrifugal force due to curvature. The axial flow is symmetric about the plane passing through the center of cross section at the absence of rotation. When the pipe rotates the symmetry breaks down. Due to Coriolis force the strength of the axial flow is shifted towards the lower portion of the cross section. Finally, the centrifugal force dominates the Coriolis force and symmetry is attained. But for higher rotation Coriolis force is too high to be dominated by the centrifugal force. As a result symmetry is not attained.

5. Conclusions

The spectral numerical solutions have been presented for the magnetohydrodynamic rotating curved flow geometry. The computations are visualized with MAPLE software and indicate the following:

1) The anti-clock wise rotating vortex in the upper portion is stronger than the clock wise rotating vortex in the lower portion for high T_r.

2) The two-vortex changes their position in anti-clock wise rotating manner with the decrease of T_r for the effect of magnetic field and rotation.

3) The maximum flux has been found when the effect of magnetic field and rotation tends to balance each other. At the maximum flux and high magnetic field the four-vortex solution has been observed.

The present study has aimed to further reveal the effects of magnetic field on Newtonian flow in rotating curved vessels, motivated by astronaut response to megnetospheric effects during spacecraft re-entry (Busby [19] ). It is being considered viscoelastic effects (Tripathi and Beg [20] ) which arise in smaller vessels, using the spectral algorithm and the results of these computations will be reported imminently.

References