Open Journal of Fluid Dynamics
Vol.4 No.2(2014), Article
ID:46085,8
pages
DOI:10.4236/ojfd.2014.42011
Thermal Radiation, Joule Heating, and Viscous Dissipation Effects on MHD Forced Convection Flow with Uniform Surface Temperature
M. Y. Abdollahzadeh Jamalabadi1,2, Jae Hyun Park3*
1Maritime University of Chabahar, Chabahar, Iran
2Graduate School of Mechanical and Aerospace Engineering, Gyeongsang National University, Jinju, South Korea
3Department of Aerospace and System Engineering, Research Center for Aircraft Parts Technology, Gyeongsang National University, Jinju, South Korea
Email: my.abdollahzadeh@gnu.ac.kr, my.abdollahzadeh@cmu.ac.ir, muhammad_yaghoob@yahoo.com, *parkj@gnu.ac.kr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 10 May 2014; accepted 18 May 2014
ABSTRACT
In this paper, we studied the effects of thermal radiation, Joule heating and viscous dissipation on forced convection flow in a magnetohydrodynamics (namely MHD) pump in rectangular channel with uniform surface temperature. Numerical results were obtained by solving the nonlinear governing momentum and energy equations with steady state fully developed assumptions by finite difference method. The Lorentz force in momentum and Joule heating, and viscous dissipation in energy equation with the Rossel and approximation are assumed to increase the knowledge of the details of the temperature and flow field in order to design a MHD pump. The purpose of this study is the parametric study of a Newtonian fluid in a MHD pump. The values of maximum velocity, fully developed Nusselt number for different values of magnetic density flux, Brinkman number, viscous heating and radiation number are obtained. However, the maximum temperature stays almost constant with magnetic field, as current increases, the velocity and the temperature increase too. Besides, the increase of thermal radiation number causes the increase in effective thermal conductivity and decrease in thermal boundary layer and the Nusselt number at wall.
Keywords:Forced Convection, Thermal Radiation, Magnetohydrodynamic Pump, Internal Heating, Viscous Dissipation, Roseland Model

1. Introduction
Laminar heat transfer to incompressible viscous Newtonian and non-Newtonian fluids in tubes is a problem of considerable industrial significance, due to its application especially in heat exchanger designs, packed-bed combustors, catalytic converters, materials-processing applications, such as extrusion, metal forming, continuous casting, as well as wire and glass fiber drawing. This problem has been therefore considered in many papers. A detailed review of literature being performs here. The work of Brinkman [1] appears to be the first theoretical work dealing with heat generated by viscous dissipation. The temperature distribution in the entrance region of a circular pipe at the wall of which was maintained at either the constant temperature of the entering fluid or constant heat-flux was examined. The highest temperatures were, not surprisingly, discovered to be localized in the wall region. Lin [2] studied laminar heat-transfer to a non-Newtonian Couette flow with pressure gradient using the power-law model. The effects of pressure gradient and viscous dissipation on the heat transfer were discussed. Using a functional analysis method, Lahjomri [3] analytically studied thermally-developing laminar Hartman flow through a parallel-plate channel, with a prescribed transversal uniform magnetic field, including both viscous dissipation, Joule heating and axial heat-conduction with uniform heat-flux. In a recent study, Nield et al. [4] investigated the thermal development of forced convection in a parallel plate channel filled by a saturated porous medium, with walls held at a uniform temperature, and with the effects of axial conduction and viscous dissipation included. Davaa et al. [5] numerically studied fully-developed laminar heattransfer to non-Newtonian fluids flowing between parallel plates with the axial movement of one of the plates with an emphasis on the viscous-dissipation effect. Increasing the Brinkman number increased the heat-transfer rates at the heated wall when the movement direction of the upper plate was the same as the direction of the main flow, while the opposite is true for the movement of the upper plate in the opposite direction. Hashemabadi et al. [6] obtained an analytical solution to predict the fully-developed, steady and laminar heat-transfer of viscoelastic fluids between parallel plates. Their results emphasized the significant effect of viscous heating on the Nusselt number. Furthermore recently Hamid et al. [7] studied the effects of radiation on Marangoni convection over a flat surface, and Chamkha et al. [8] studied that effect on a non-isothermal wedge not in a channel.
The aim of the present study is to investigate analytically the effect of viscous dissipation on steady-state laminar heat transfer in a Poiseuille flow between plane parallel plates in a rectangular channel with a simultaneous pressure gradient, Lorentz force and joule heating effect. The effect of Brinkman number on the temperature profile and the Nusselt number is obtained for the constant temperature boundary-condition from radiate surfaces.
2. Governing Equations and Numerical Method
Consider steady, hydrodynamically and thermally fully-developed, laminar flow of an incompressible fluid between two parallel plates (Figure 1). The thermal conductivity and the thermal diffusivity of the fluid are considered to be independent of temperature. Fluid viscosity is modeled by the power law. Furthermore magnetic and electric properties are constant. The both plate is assumed to be in a stationary.
The axial heat-conductions in the fluid and in the wall are neglected. The momentum equation in the x-direction is described as final stage

Figure 1. Geometry of problem.
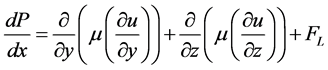 (1)
(1)
In which Lorentz force can be written as:
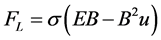
where E is electric field intensity in z-direction, B is magnetic density in y-direction and σ is electrical conductivity of the fluids. The conservation of energy, including the effect of the viscous dissipation, can be written as follows:
 (2)
(2)
where the second term on the right-hand side is the viscous-dissipation term and third term is joule heating. Also the Energy equation by considering the Rossel and approximation for the radiative flux is used which assumes that the radiative heat flux vector in a gray optically thick medium corresponds to the blackbody emissive power (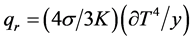 ) and suggest the effective thermal conductivity (
) and suggest the effective thermal conductivity (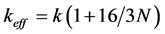 ) [9] . Under the following boundary conditions:
) [9] . Under the following boundary conditions:
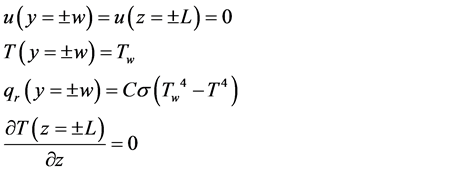 (3)
(3)
where the C is plotted as a function of N and presented in Figure 2 [9] . In fully-developed flow, it is usual to utilize the mean fluid temperature, Tm, rather than the center-line temperature when defining the Nusselt number. By introducing the non-dimensional quantities
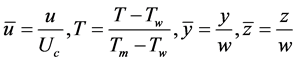 (4)
(4)
Governing Equations based on non-dimensional parameters can be re-written as
 (5)
(5)
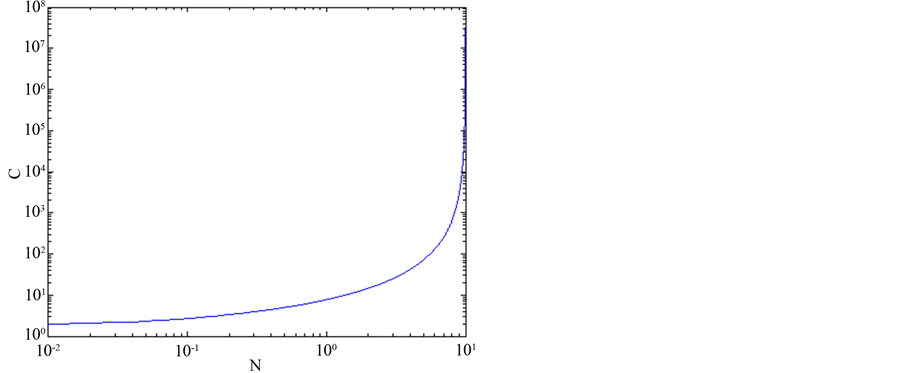
Figure 2. Thermal boundary coefficient.
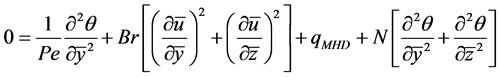
When the temperature profile is fully developed one can write 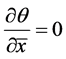 (Bejan [10] ). The thermal boundary conditions of Equation (5) are
(Bejan [10] ). The thermal boundary conditions of Equation (5) are
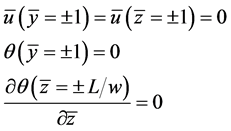 (6)
(6)
3. Results and Discussion
To solve the governing nonlinear differential equations, an in-house finite-volume code is developed and utilized. The code is based on structured grid. It generates a uniform grid consisting of a number of nodes in the yand z-directions. This method is utilized to assure high accuracy. A minimum of 2000 nodes are assumed. The residuals for velocity and temperature are set at 1e − 6 .The program uses the input data and solve the momentum equations to obtain velocity field along the MHD pump. Then, temperature distribution is obtained by solving the energy equation. For verification purposes, Figure 3 shows the current as it is compared with a computational model known case (flow inside a rectangular duct) by Wang et al. [11] . As shown, the volumetric flow rates for both studies show a similar trend.
The effect of magnetic flux density on maximum velocity and volumetric flow rate of the MHD pump is shown by Figure 4. The effect of electric current on velocity profile and volumetric flow rate of the MHD pump is shown by Figure 5. As shown, the maximum velocity and then volumetric flow rate increase with increasing magnetic flux density and electric current. The effect of Brinkman number and MHD heat generation on temperature profiles are presented of Figure 6 and Figure 7 respectively. The Brinkman number increase the temperature profile near the wall while the joule heating increase the temperature profile near the center of the channel. As demonstrated the maximum temperature increase with increasing electric current but is not varied considerably with magnetic flux density variations. Also Figure 8 and Figure 9 present the linear increasing effect of Brinkmann number and magnetic flux on Nusselt number, respectively. Reverse effect for radiative heating on Nusselt number presented on Figure 10.
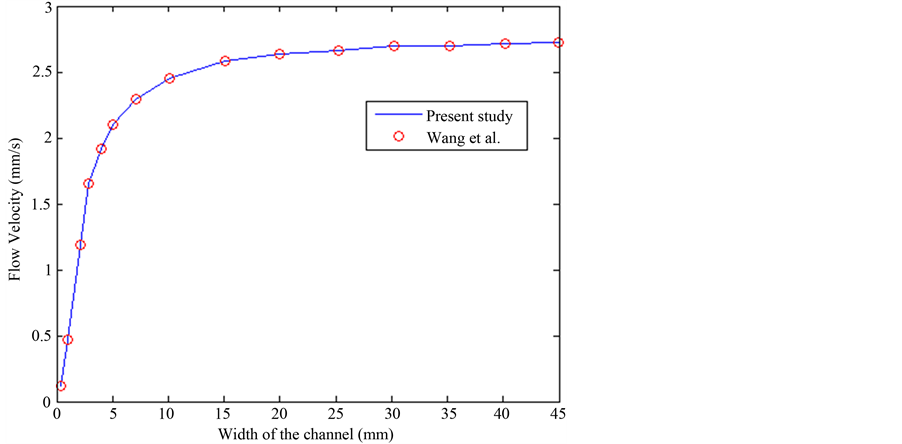
Figure 3. Comparison of the flow velocity as a function of channel width by [11] (channel depth = 2 mm, I = 0.5 A , B = 18 mT).
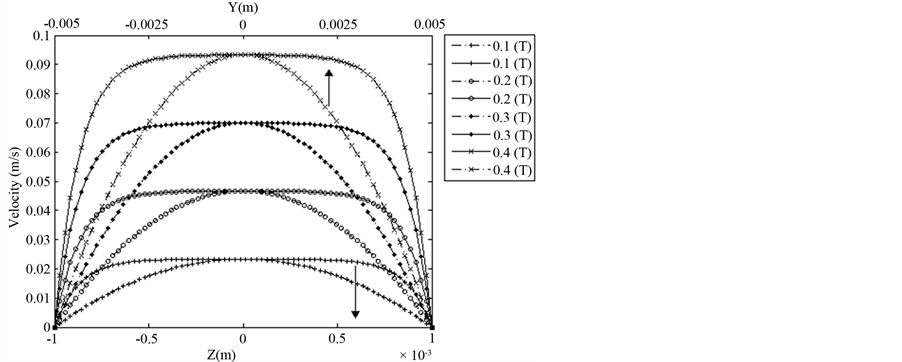
Figure 4. Magnetic flux density via velocity profile. Pr = 0.1, I = 0.4, qMHD = 0.
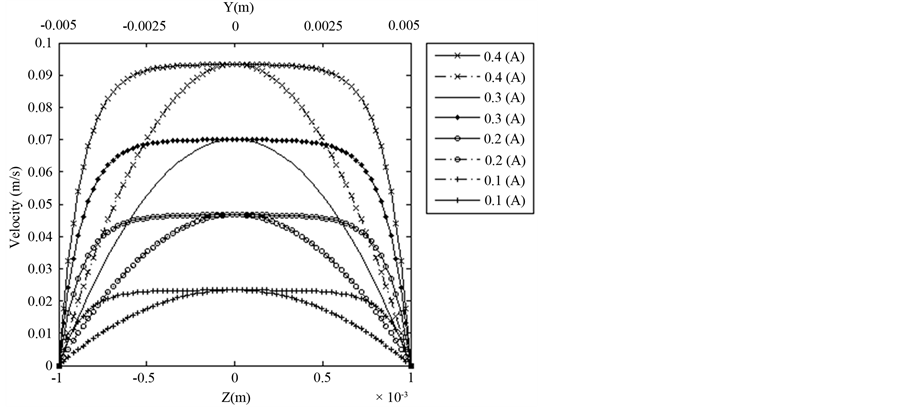
Figure 5. Maximum velocity as a function of electric current, where B is kept constant at 0.4.
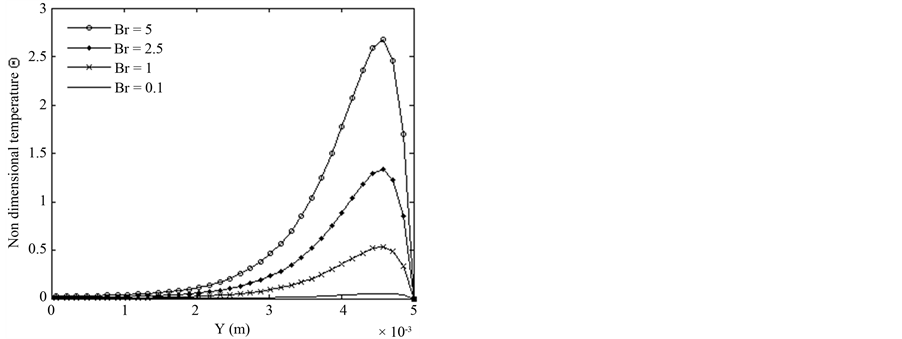
Figure 6. Effect of Brinkman number on temperature profile Pr = 0.1, I = 0.4, qMHD = 0.

Figure 7. Effect of heat generation on temperature profile Pr = 0.1, I = 0.4.
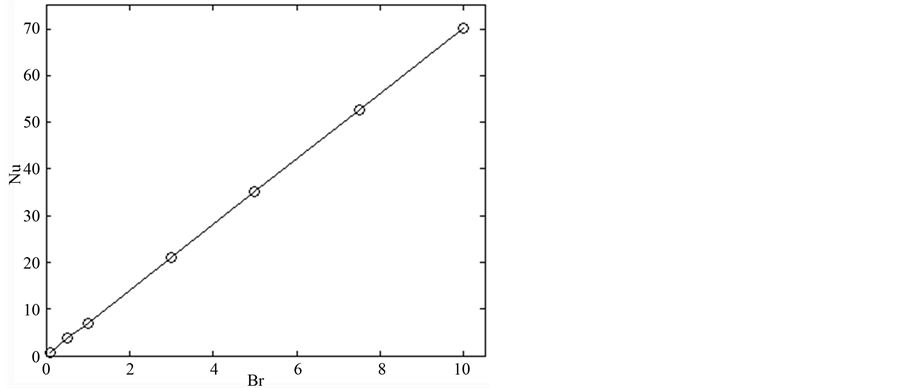
Figure 8. Effect of brinkman number on average nusselt number Pr = 0.1, I = 0.4, qMHD = 0, B = 0.4.
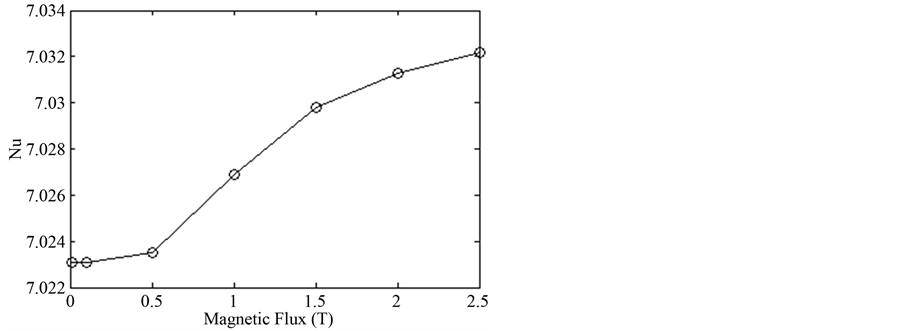
Figure 9. Effect of magnetic flux on Nusselt number, Br = 1, I = 0.4, qMHD = 0.
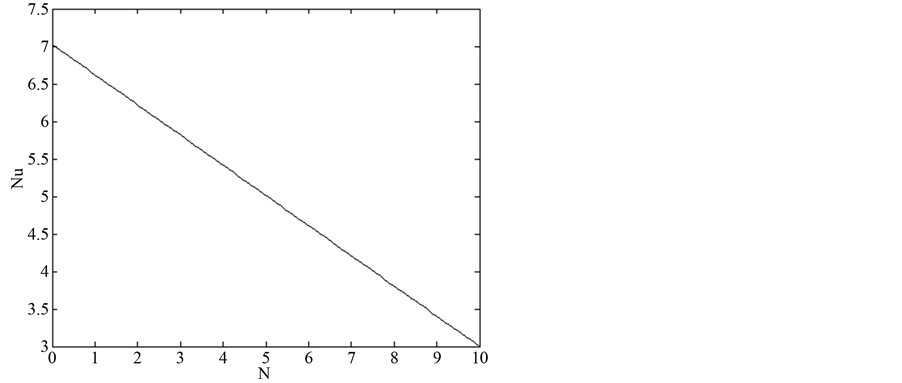
Figure 10. Effect of magnetic flux on Nusselt number, Br = 1, I = 0.4, qMHD = 0, B = 0.
4. Conclusion
In this study, a finite-difference code is used for solving momentum and energy equations and the velocity and the temperature field has been derived for the laminar, steady, convective heat-transfer problem in a Poiseuille flow between plane parallel plates with a simultaneous pressure-gradient and the Lorentz force. Interest has been focused on the influence of the viscous dissipation and internal heating ratio. The effect of the Brinkman number on the Nusselt number has been discussed in terms of the energy balance. The maximum velocity and volumetric flow rate increase with increasing magnetic flux density and electric current. The maximum temperature increases with increasing electric current but is not varied considerably with magnetic flux density variations. As illustrated the Brinkman number increases the temperature profile near the wall while the joule heating increases the temperature profile near the center of the channel. The results show that for the thermally fully-developed, a strong influence of viscous dissipation on the heat transfer for higher values of Br (Br > 1) has been observed, while this influence is found to be negligible for lower values of Br. Finally by increase of Brinkmann number and magnetic flux, and decrease of radiative heating has linear increasing effect on Nusselt number.
Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (NRF-2012R1A1A1042920).
References
- Brinkman, H.C. (1951) Heat Effects in Capillary Flow I. Applied Scientific Research, 2, 120-124. http://dx.doi.org/10.1007/BF00411976
- Lin, S.H. (1979) Heat Transfer to Plane Non-Newtonian Couette Flow. International Journal of Heat and Mass Transfer, 22, 1117-1123. http://dx.doi.org/10.1016/0017-9310(79)90184-4
- Lahjomri, J., Zniber, K., Oubarra, A. and Alemany, A. (2003) Heat Transfer by Laminar Hartmanns Flow in the Thermal Entrance-Region with Uniform Wall Heat-Flux: The Graetz Problem Extended. Energy Conversion and Management, 44, 11-34. http://dx.doi.org/10.1016/S0196-8904(02)00048-1
- Nield, D.A., Kuznetzov, A.V. and Xiong, M. (2003) Thermally-Developing Forced Convection in a Porous Medium: Parallel-Plate Channel with Walls at a Uniform Temperature, with Axial Conduction and Viscous Dissipation Effects. International Journal of Heat and Mass Transfer, 46, 643-651.http://dx.doi.org/10.1016/S0017-9310(02)00327-7
- Davaa, G., Shigechi, T. and Momoki, S. (2004) Effect of Viscous Dissipation on Fully-Developed Heat Transfer of Non-Newtonian Fluids in Plane Laminar Poiseuille-Couette Flow. International Journal of Heat and Mass Transfer, 31, 663-672. http://dx.doi.org/10.1016/S0735-1933(04)00053-3
- Hashemabadi, S.H., Etemad, S.Gh and Thibault, J. (2004) Forced-Convection Heat-Transfer of Couette-Poiseuille Flow of Non-Linear Viscoelastic Fluids between Parallel Plates. International Journal of Heat and Mass Transfer, 47, 3985-3991.
- Abdul Hamid, R., Arifin, N.M. and Nazar, R. (2013) Effects of Radiation, Joule Heating and Viscous Dissipation on MHD Marangoni Convection over a Flat Surface with Suction and Injection. World Applied Sciences Journal, 21, 933-938.
- Chamkha, A.J., Mujtaba, M., Quadri, A. and Issa, C. (2003) Thermal Radiation Effects on MHD Forced Convection Flow Adjacent to a Non-Isothermal Wedge in the Presence of a Heat Source or Sink. Heat and Mass Transfer, 39, 305-312.
- Siegel, R. and Howell, J.R. (1992) Thermal Radiation Heat Transfer. Hemisphere Publishing Corporation, Washington DC.
- Morega, Al.M. and Bejan, A. (1993) Heatline Visualisation of Forced Convection Laminar Boundary Layers. International Journal of Heat and Mass Transfer, 36, 3957-3966. http://dx.doi.org/10.1016/0017-9310(93)90146-W
- Wang, P.J., Chang, C.Y. and Chang, M.-L. (2004) Simulation of Two-Dimensional Fully Developed Laminar Flow for a Magneto-Hydrodynamic (MHD) Pump. Biosensors and Bioelectronics, 20, 115-121. http://dx.doi.org/10.1016/j.bios.2003.10.018
NOTES

*Corresponding author.

