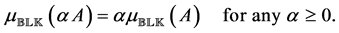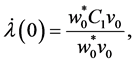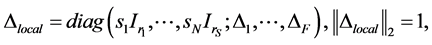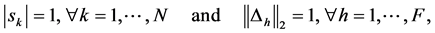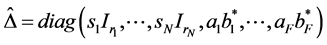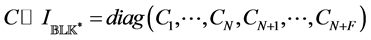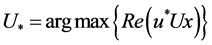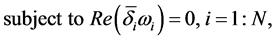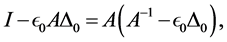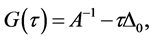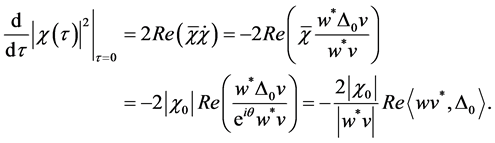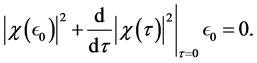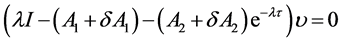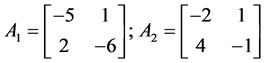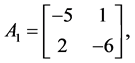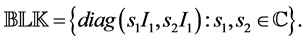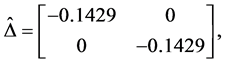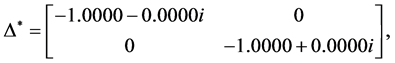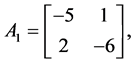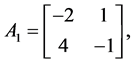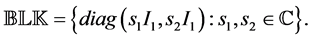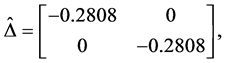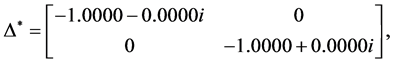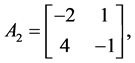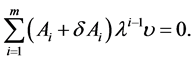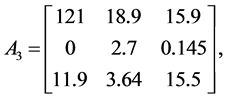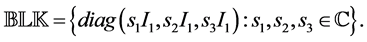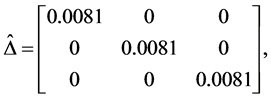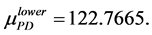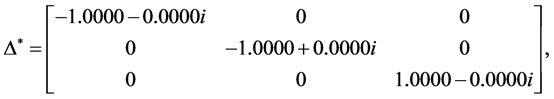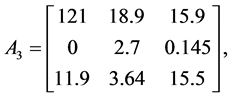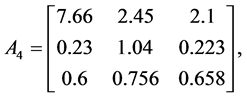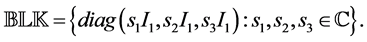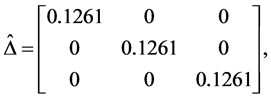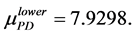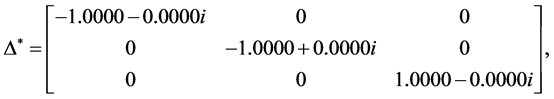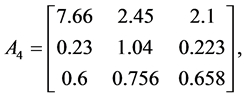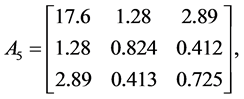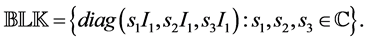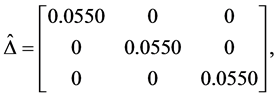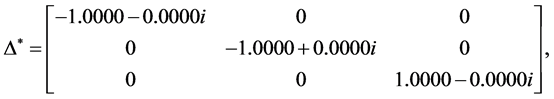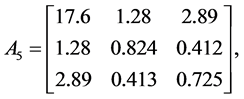Open Journal of Applied Sciences
Vol.07 No.07(2017), Article ID:77786,17 pages
10.4236/ojapps.2017.77028
Computing Structured Singular Values for Delay and Polynomial Eigenvalue Problems
Mutti-Ur Rehman1, Danish Majeed2, Naila Nasreen3, Shabana Tabassum1
1Department of Mathematics and Statistics, The University of Lahore, Gujrat Campus, Gujrat, Pakistan
2Department of Applied Physics, Federal Urdu University of Arts, Science and Technology, Islamabad, Pakistan
3Department of Mathematics, COMSATS Institute of Information Technology Islamabad Campus, Islamabad, Pakistan

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 27, 2017; Accepted: July 18, 2017; Published: July 21, 2017
ABSTRACT
In this article the computation of the Structured Singular Values (SSV) for the delay eigenvalue problems and polynomial eigenvalue problems is presented and investigated. The comparison of bounds of SSV with the well-known MATLAB routine mussv is investigated.
Keywords:
m-Values, Block Diagonal Uncertainties, Spectral Radius, Low-Rank Approximation, Delay Eigenvalue Problems, Polynomial Eigenvalue Problems

1. Introduction
The m-values [1] is an important mathematical tool in control theory; it allows discussing the problem arising in the stability analysis and synthesis of control systems to quantify the stability of a closed-loop linear time-invariant systems subject to structured perturbations. The structures addressed by the SSV is very general and allows covering all types of parametric uncertainties that can be incorporated into the control system by using real and complex Linear Fractional Transformations LFT’s. For more detail please see [1] - [7] and the references therein for the applications of SSV.
The versatility of the SSV comes at the expense of being notoriously hard, in fact Non-deterministic Polynomial time that is NP hard [8] to compute. The numerical algorithms which are being used in practice provide both upper and lower bounds of SSV. An upper bound of the SSV provides sufficient conditions to guarantee robust stability analysis of feedback systems, while a lower bound provides sufficient conditions for instability analysis of the feedback systems.
The widely used function mussv available in the Matlab Control Toolbox computes an upper bound of the SSV using diagonal balancing and Linear Matrix Inequality techniques [9] [10] . The lower bound is computed by using the generalization of power method developed in [11] [12] .
In this paper the comparison of numerical results to approximate the lower bounds of the SSV associated with mixed real and pure complex uncertainties is presented.
Overview of the article. Section 2 provides the basic framework. In particular, it explains how the computation of the SSV can be addressed by an inner-outer algorithm, where the outer algorithm determines the perturbation level  and the inner algorithm determines a (local) extremizer of the structured spectral value set. In Section 3 it is explained that how the inner algorithm works for the case of pure complex structured perturbations. An important characterization of extremizers shows that one can restrict himself to a manifold of structured perturbations with normalized and low-rank blocks. A gradient system for finding extremizers on this manifold is established and analyzed. The outer algorithm is addressed in Section 4, where a fast Newton iteration for determining the correct perturbation level
and the inner algorithm determines a (local) extremizer of the structured spectral value set. In Section 3 it is explained that how the inner algorithm works for the case of pure complex structured perturbations. An important characterization of extremizers shows that one can restrict himself to a manifold of structured perturbations with normalized and low-rank blocks. A gradient system for finding extremizers on this manifold is established and analyzed. The outer algorithm is addressed in Section 4, where a fast Newton iteration for determining the correct perturbation level  is developed. Finally, Section 5 presents a range of numerical experiments to compare the quality of the lower bounds to those obtained with mussv.
is developed. Finally, Section 5 presents a range of numerical experiments to compare the quality of the lower bounds to those obtained with mussv.
2. Framework
Consider a matrix 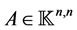 where
where 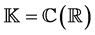 and an underlying perturba- tion set with prescribed block diagonal structure,
and an underlying perturba- tion set with prescribed block diagonal structure,
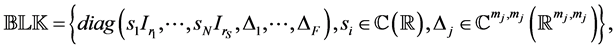 (1)
(1)
where 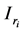 denotes the
denotes the 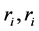 identity matrix. Each of the scalars
identity matrix. Each of the scalars 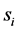 and the
and the 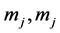 matrices
matrices 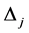 may be constrained to stay real in the definition of
may be constrained to stay real in the definition of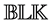 . The integer N denotes the number of repeated scalar blocks (that is, scalar multiples of the identity) and F denotes the number of full blocks. This implies
. The integer N denotes the number of repeated scalar blocks (that is, scalar multiples of the identity) and F denotes the number of full blocks. This implies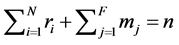 . In order to distinguish complex and real scalar blocks, assume that the first
. In order to distinguish complex and real scalar blocks, assume that the first  blocks are complex while the (possibly) remaining
blocks are complex while the (possibly) remaining 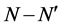 blocks are real. Similarly assume that the first
blocks are real. Similarly assume that the first 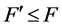 full blocks are complex and the remaining
full blocks are complex and the remaining 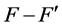 blocks are real. The literature (see, e.g., [1] ) usually does not consider real full blocks, that is,
blocks are real. The literature (see, e.g., [1] ) usually does not consider real full blocks, that is,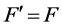 . In fact, in control theory, full blocks arise from uncertainties associated to the frequency response of a system, which is complex-valued.
. In fact, in control theory, full blocks arise from uncertainties associated to the frequency response of a system, which is complex-valued.
For simplicity, assume that all full blocks are square, although this is not necessary and our method extends to the non-square case in a straightforward way. Similarly, the chosen ordering of blocks should not be viewed as a limiting assumption; it merely simplifies notation.
The following definition is given in [1] , where 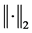 denotes the matrix 2-norm and
denotes the matrix 2-norm and 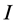
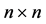
Definition 2.1. [13] . Let 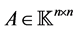
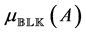
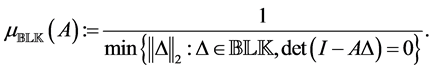
In Definition 2.1, 
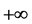
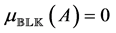
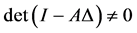
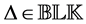
Note that 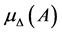
For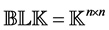
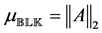
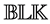
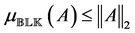
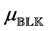
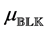
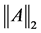
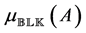
The important special case when 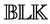
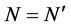
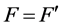
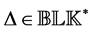
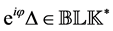
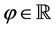
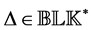
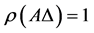
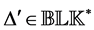
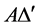
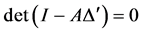
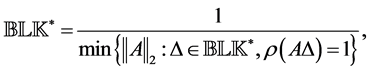
where 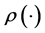
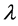
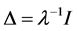
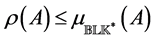
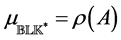
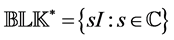
matrix 2-norm are included as special cases of the SSV.
2.1. A Reformulation Based on Structured Spectral Value Sets [13]
The structured spectral value set of 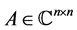
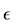
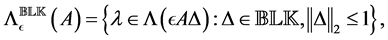
where 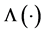
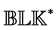
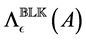
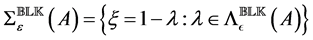
allows us to express the SSV defined in Equation (2) as
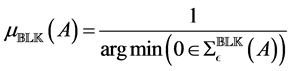
that is, as a structured distance to singularity problem. This gives us that 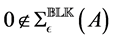
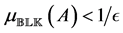
For a purely complex perturbation set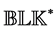
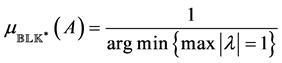
where 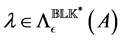
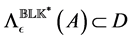
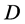
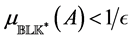
2.2. Problem under Consideration [13]
Let us consider the minimization problem
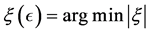
where 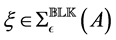
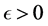
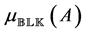
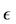
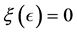
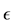
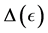
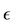
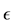
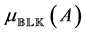
The case of a purely complex perturbation set 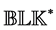
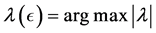
where 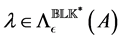
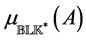
3. Pure Complex Perturbations [13]
In this section, we consider the solution of the inner problem discussed in
Equation (9) in the estimation of 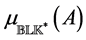
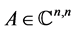
perturbation set
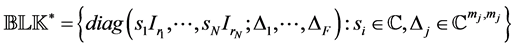
3.1. Extremizers
Now, make use of the following standard eigenvalue perturbation result, see, e.g., [15] . Here and in the following, denote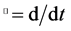
Lemma 3.1. Consider a smooth matrix family 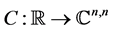
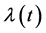
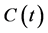
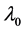
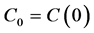
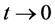
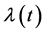
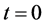
where 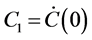
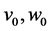

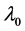
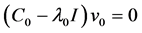
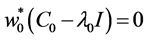
Our goal is to solve the maximization problem discussed in Equation (9), which requires finding a perturbation 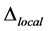
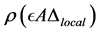
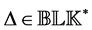
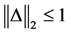
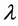
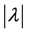
Definition 3.2. [13] . A matrix 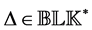
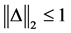
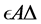
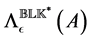
The following result provides an important characterization of local extre- mizers.
Theorem 3.3. [13] . Let
be a local extremizer of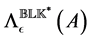
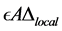
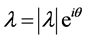
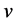
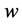
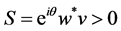

such that the size of the components 
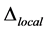
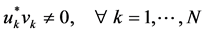
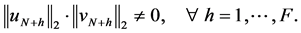
then
that is, all blocks of 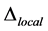
The following theorem allows us to replace full blocks in a local extremizer by rank-1 matrices.
Theorem 3.4. [13] . Let 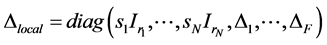
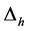
singular vectors 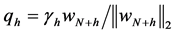
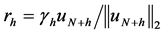
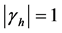
is also a local extremizer, i.e.,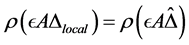
Remark 3.1. [13] . Theorem 3.3 allows us to restrict the perturbations in the structured spectral value set shown in Equation (4) to those with rank-1 blocks, which was also shown in [1] . Since the Frobenius and the matrix 2-norms of a rank-1 matrix are equal, one can equivalently search for extremizers within the submanifold
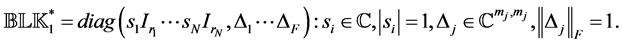
3.2. A system of ODEs to Compute Extremal Points of 
In order to compute a local maximizer for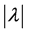
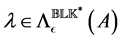
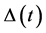
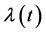
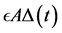
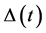
Orthogonal projection onto
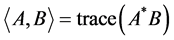
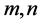
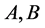
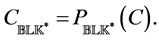
denote the orthogonal projection, with respect to the Frobenius inner product, of a matrix 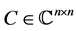
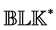
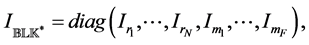
where 
Lemma 3.5. [13] . For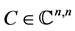
denote the block diagonal matrix obtained by entrywise multiplication of C with
the matrix 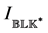
onto 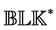
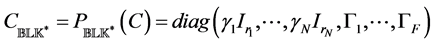
where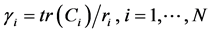
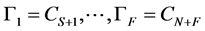
The local optimization problem [13] . Let us recall the setting from Section (3.1): assume that 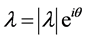
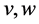
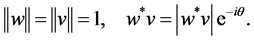
As a consequence of Lemma 3.1, see also Equation (15), to have
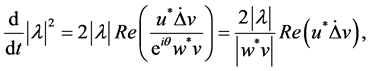
where 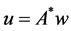
Letting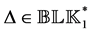
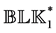
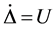
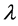
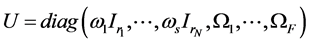
as a solution of the optimization problem
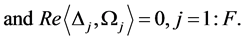
The target function in Equation (20) follows from Equation (19), while the constraints in Equation (21) ensure that 
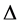
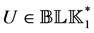
Lemma 3.6. [13] . With the notation introduced above and 
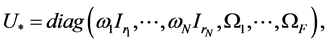
with
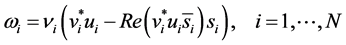
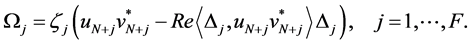
Here, 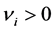
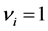
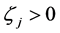
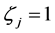
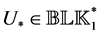
Corollary 3.7. [13] . The result of Lemma 3.6 can be expressed as
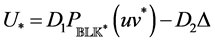
where 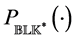
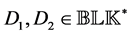
matrices with 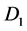
Proof. The statement is an immediate consequence of Lemma 3.5.
The system of ODEs. Lemma 3.6 and Corollary 3.7 suggest to consider the following differential equation on the manifold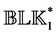
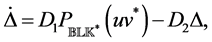
where 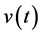
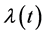
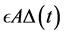
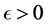
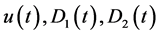
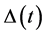
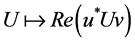
The following result follows directly from Lemmas 3.1 and 3.6.
Theorem 3.8. [13] . Let 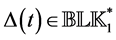
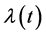
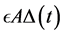
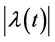
The following lemma establishes a useful property for the analysis of stationary points of Equation (26).
Lemma 3.9. [13] . Let 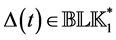
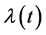
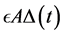
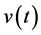
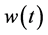
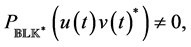
where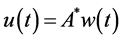
Remark 3.3. The choice of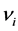

The following result characterizes stationary points of Equation (26).
Theorem 3.10. [13] . Assume that 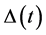
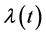
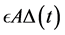
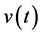
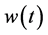
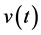
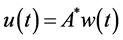
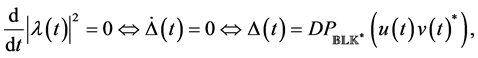
for a specific real diagonal matrix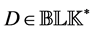
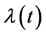
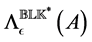
3.3. Projection of Full Blocks on Rank-1 Manifolds [13]
In order to exploit the rank-1 property of extremizers established in Theorem 3.4, one can proceed in complete analogy to [16] in order to obtain for each full block an ODE on the manifold M of (complex) rank-1 matrices. The derivation of this system of ODEs is straightforward; the interested reader can see [17] for full details.
The monotonicity and the characterization of stationary points follows analogously to those obtained for Equation (26); and also refer to [16] for the proofs. As a consequence one can use the ODE in Equation (28) instead of Equation (26) and gain in terms of computational complexity.
3.4. Choice of Initial Value Matrix and 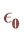
In our two-level algorithm for determining 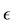
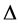
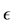
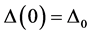
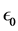
For the moment, let us assume that A is invertible and write
which aim to have as close as possible to singularity. To determine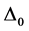
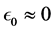
and let denote 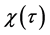
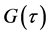
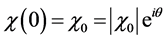
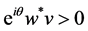
In order to have the locally maximal decrease of 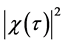

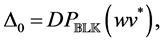
where the positive diagonal matrix D is chosen such that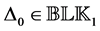
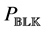
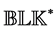
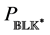
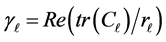
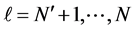
Note that there is no need to form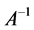
be paid to the scaling. Since the largest eigenvalue of A is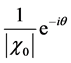
to be scaled accordingly.
A possible choice for 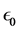

This gives
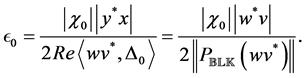
This can be improved in a simple way by computing this expression for 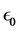
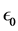
Another possible, very natural choice for 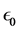
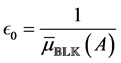
where 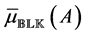
4. Fast Approximation of 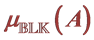
This section discuss the outer algorithm for computing a lower bound of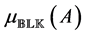
Purely Complex Perturbations
In the following let 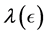
computed by determining the stationary points 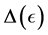
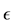
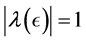
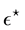
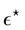
contained in the unit disk and its boundary 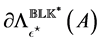
circle. This provides a lower bound 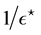
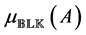
Now make the following generic assumption.
Assumption 4.1. [13] . For a local extremizer 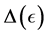
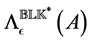
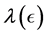
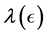
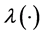
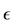
The following theorem gives an explicit and easily computable expression for the derivative of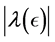
Theorem 4.1. [13] . Suppose that Assumption 4.1 holds for 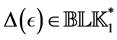
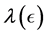
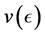
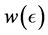
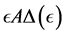
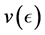
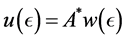
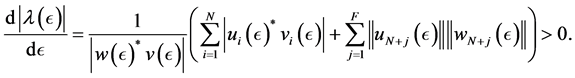
5. Numerical Experimentation
This section provides the comparison of the lower bounds of SSV computed by well-known Matlab function mussv and the algorithm [13] .
We consider the following delay eigenvalue problem of the form:
where,
and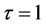
Example 1. Consider the following two dimensional matrix 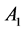
along with the perturbation set
Apply the Matlab routine mussv, one can obtain the perturbation 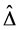
and 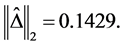
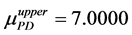
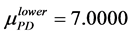
By using the algorithm [13] , one can obtain the perturbation 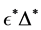
and 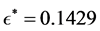
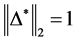
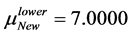
In the following Table 1, it is presented the comparison of the bounds of SSV computed by MUSSV and the algorithm [13] for the matrix 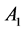
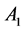
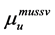
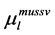
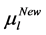
and
Example 2. Consider the following two dimensional matrix 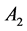
along with the perturbation set
Apply the Matlab routine mussv, one can obtain the perturbation 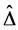
Table 1. Comparison of lower bounds of SSV with MATLAB function mussv.
and 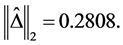
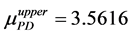
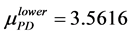
By using the algorithm [13] , one can obtain the perturbation 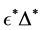
and 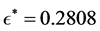
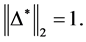
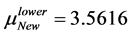
In Table 2, it is presented the comparison of the bounds of SSV computed by MUSSV and the algorithm [13] for the matrix 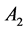
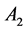
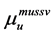
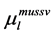
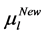
and
We consider the polynomial eigenvalue problems.
Consider the quadratic eigenvalue problem of the form:
Example 3. Consider the following three dimensional matrix 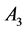
along with the perturbation set
Apply the Matlab routine mussv, one can obtain the perturbation 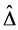
Table 2. Comparison of lower bounds of SSV with MATLAB function mussv.
and 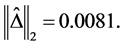
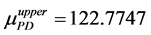
By using the algorithm [13] , one can obtain the perturbation 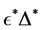
and 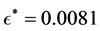
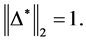
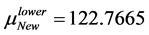
In Table 3, it is presented the comparison of the bounds of SSV computed by MUSSV and the algorithm [13] for the matrix 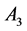
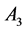
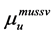
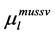
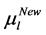
and
Example 4. Consider the following three dimensional matrix 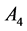
Table 3. Comparison of lower bounds of SSV with MATLAB function mussv.
along with the perturbation set
Apply the Matlab routine mussv, one can obtain the perturbation 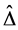
and 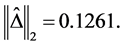
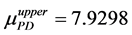
By using the algorithm [13] , one can obtain the perturbation 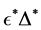
and 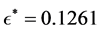
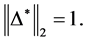
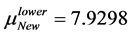
In Table 4, it is presented the comparison of the bounds of SSV computed by MUSSV and the algorithm [13] for the matrix 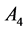
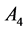
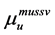
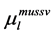
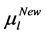
and
Example 5. Consider the following three dimensional matrix 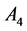
Table 4. Comparison of lower bounds of SSV with MATLAB function mussv.
along with the perturbation set
Apply the Matlab routine mussv, one can obtain the perturbation 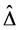
and 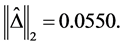
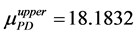
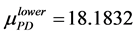
By using the algorithm [13] , one can obtain the perturbation 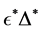
and 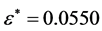
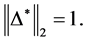
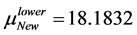
In Table 5, it is presented the comparison of the bounds of SSV computed by MUSSV and the algorithm [13] for the matrix 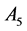
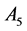
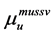
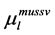
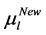
and
Table 5. Comparison of lower bounds of SSV with MATLAB function mussv.
6. Conclusion
In this article the problem of approximating structured singular values for the delay eigenvalue and polynomial eigenvalue problems is considered. The obtained results provide a characterization of extremizers and gradient systems, which can be integrated numerically in order to provide approximations from below to the structured singular value of a matrix subject to general pure complex and mixed real and complex block perturbations. The experimental results show the comparison of the lower bounds of structured singular values with once computed by MUSSV and alogorithm [13] .
Cite this paper
Rehman, M.-U., Majeed, D., Nasreen, N. and Tabassum, S. (2017) Computing Structured Singular Values for Delay and Polynomial Eigenvalue Problems. Open Journal of Applied Sciences, 7, 348-364. https://doi.org/10.4236/ojapps.2017.77028
References
- 1. Packard, A. and Doyle, J. (1993) The Complex Structured Singular Value. Automatica, 29, 71-109.
https://doi.org/10.1016/0005-1098(93)90175-S - 2. Bernhardsson, B. and Rantzer, A. and Qiu, L. (1994) Real Perturbation Values and Real Quadratic Forms in a Complex Vector Space. Linear Algebra and Its Applications, 1, 131-154.
- 3. Chen, J., Fan, M.K.H. and Nett, C.N. (1996) Structured Singular Values with Nondiagonal Structures. I. Characterizations. IEEE Transactions on Automatic Control, 41, 1507-1511.
- 4. Hinrichsen, D. and Pritchard, A.J. (2005) Mathematical Systems Theory I, Vol. 48 of Texts in Applied Mathematics. Springer-Verlag, Berlin.
- 5. Karow, M., Kokiopoulou, E. and Kressner, D. (2010) On the Computation of Structured Singular Values and Pseudospectra. Systems & Control Letters, 59, 122-129.
https://doi.org/10.1016/j.sysconle.2009.12.007 - 6. Karow, M., Kressner, D. and Tisseur, F. (2006) Structured Eigenvalue Condition Numbers. SIAM Journal on Matrix Analysis and Applications, 28, 1052-1068.
https://doi.org/10.1137/050628519 - 7. Qiu, L., Bernhardsson, B., Rantzer, A., Davison, E.J., Young, P.M. and Doyle, J.C. (1995) A Formula for Computation of the Real Stability Radius. Automatica, 31, 879-890.
- 8. Braatz, R.P., Young, P.M., Doyle, J.C. and Morari, M. (1994) Computational Complexity of µ Calculation. IEEE Transactions on Automatic Control, 39, 1000-1002.
- 9. Fan, M.K.H., Tits, A.L. and Doyle, J.C. (1991) Robustness in the Presence of Mixed Parametric Uncertainty and Unmodeled Dynamics. IEEE Transactions on Automatic Control, 36, 25-38.
- 10. Young, P.M., Newlin, M.P. and Doyle, J.C. (1992) Practical Computation of the Mixed µ Problem. American Control Conference, 24-26 June 1992, 2190- 2194.
- 11. Packard, A., Fan, M.K.H. and Doyle, J. (1998) A Power Method for the Structured Singular Value. Proceedings of the 27th IEEE Conference on Decision and Control, 7-9 December 1988, 2132-2137.
- 12. Young, P.M., Doyle, J.C., Packard, A., et al. (1994) Theoretical and Computational Aspects of the Structured Singular Value. Systems, Control and Information, 38, 129-138.
- 13. Guglielmi, N., Rehman, M.-U. and Kressner, D. (2016) A Novel Iterative Method to Approximate Structured Singular Values. arXiv preprint arXiv:1605.04103.
- 14. Zhou, K., Doyle, J. and Glover, K. (1996) Robust and Optimal Control. Prentice Hall, New Jersey, Volume 40.
- 15. Kato, T. (2013) Perturbation Theory for Linear Operators. Springer Science & Business Media, Volume 132.
- 16. Guglielmi, N. and Lubich, C. (2011) Differential Equations for Roaming Pseudospectra: Paths to Extremal Points and Boundary Tracking. SIAM Journal on Numerical Analysis, 49, 1194-1209.
https://doi.org/10.1137/100817851 - 17. Guglielmi, N, and Lubich, C. (2013) Low-Rank Dynamics for Computing Extremal Points of Real Pseudospectra. SIAM Journal on Matrix Analysis and Applications, 34, 40-66.
https://doi.org/10.1137/120862399 - 18. Lehoucq, R.B. and Sorensen, D.C. (1996) Deflation Techniques for an Implicitly Restarted Arnoldi Iteration. SIAM Journal on Matrix Analysis and Applications, 17, 789-821.
https://doi.org/10.1137/S0895479895281484 - 19. Lehoucq, R.B., Sorensen, D.C. and Yang, C. (1998) ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM, Volume 6.