Open Journal of Applied Sciences
Vol.06 No.12(2016), Article ID:72330,13 pages
10.4236/ojapps.2016.612073
A Simulation Study on the Specific Loss Power in Magnetic Hyperthermia in the Presence of a Static Magnetic Field
Kenya Murase
Department of Medical Physics and Engineering, Division of Medical Technology and Science, Faculty of Health Science, Graduate School of Medicine, Osaka University, Osaka, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 25, 2016; Accepted: November 26, 2016; Published: November 29, 2016
ABSTRACT
Our purpose in this study was to present a method for estimating the specific loss power (SLP) in magnetic hyperthermia in the presence of an external static magnetic field (SMF) and to investigate the SLP values estimated by this method under various diameters (D) of magnetic nanoparticles (MNPs) and amplitudes (H0) and frequencies (f) of an alternating magnetic field (AMF). In our method, the SLP was calculated by solving the magnetization relaxation equation of Shliomis numerically, in which the magnetic field strength at time t (H(t)) was assumed to be given by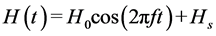 , with Hs being the strength of the SMF. We also investigated the SLP values in the case when the SMF with a field-free point (FFP) generated by two solenoid coils was used. The SLP value in the quasi steady state (SLPqss) decreased with increasing Hs. The plot of the SLPqss values against the position from the FFP became narrow as the gradient strength of the SMF (Gs) increased. Conversely, it became broad as Gs decreased. These results suggest that the temperature rise and the area of local heating in magnetic hyperthermia can be controlled by varying the Hs and Gs values, respectively. In conclusion, our method will be useful for estimating the SLP in the presence of both the AMF and SMF and for designing an effective local heating system for magnetic hyperthermia in order to reduce the risk of overheating surrounding healthy tissues.
, with Hs being the strength of the SMF. We also investigated the SLP values in the case when the SMF with a field-free point (FFP) generated by two solenoid coils was used. The SLP value in the quasi steady state (SLPqss) decreased with increasing Hs. The plot of the SLPqss values against the position from the FFP became narrow as the gradient strength of the SMF (Gs) increased. Conversely, it became broad as Gs decreased. These results suggest that the temperature rise and the area of local heating in magnetic hyperthermia can be controlled by varying the Hs and Gs values, respectively. In conclusion, our method will be useful for estimating the SLP in the presence of both the AMF and SMF and for designing an effective local heating system for magnetic hyperthermia in order to reduce the risk of overheating surrounding healthy tissues.
Keywords:
Magnetic Hyperthermia, Magnetic Nanoparticle, Specific Loss Power, Alternating Magnetic Field, Static Magnetic Field, Magnetization Relaxation, Field-Free Point

1. Introduction
Hyperthermia is one of the promising approaches to cancer therapy [1] [2] . Hyperthermia with use of magnetic nanoparticles (MNPs) (magnetic hyperthermia) was developed in the 1950s [3] and is still under development in the effort to overcome the drawbacks in other hyperthermia modalities such as radiofrequency (RF)-capacitive hyperthermia and ultrasound hyperthermia [4] [5] .
MNPs generate heat in an alternating magnetic field (AMF) as a result of hysteresis and relaxational losses, which results in heating of the tissue in which MNPs accumulate [6] . For small MNPs, the relaxational losses caused by a delay in magnetization relaxation are dominant for heat dissipation [6] . With the development of precise methods for synthesizing functionalized MNPs [7] , MNPs with functionalized surfaces, which have high specificity for tumor tissue, have been developed as heating elements for magnetic hyperthermia [8] . Recently, MNPs with a higher heating efficiency, i.e., specific loss power (SLP) have also been actively developed [9] . Furthermore, there is renewed interest in magnetic hyperthermia as a treatment modality for cancer, especially when it is combined with other, more traditional therapeutic approaches such as the co-delivery of anticancer drugs [10] or radiation therapy [11] . From these aspects, magnetic hyperthermia has received much recent attention.
The estimation of SLP is important for evaluating the heating efficiency of MNPs, for optimizing the parameters of AMF, and for the optimal design of MNPs in an attempt to establish the effectiveness of magnetic hyperthermia. Rosensweig’s model [6] has often been used for the estimation of SLP. His model, however, is based on the so-called linear magnetization assumption [12] , and thus it is said that his model is strictly valid only in the limit of small amplitude and frequency of AMF. Recently, we have presented three methods for estimating SLP and compared the SLP values estimated by the three methods under various conditions of MNPs and AMF [13] . Furthermore, we investigated the validity of Rosensweig’s model in comparison with the numerical solution of the magnetization relaxation equation of Shliomis [13] [14] .
It is also important to heat the targeted tumor to the desired temperature without damaging the surrounding healthy tissues in order to enhance the effectiveness of magnetic hyperthermia. In 2009, Tasci et al. [15] proposed and designed a system that focuses the heat into very small regions using a static magnetic field (SMF) with a field- free point (FFP) generated by two solenoid coils, and reported that this method will be useful for making magnetic hyperthermia a more effective approach to cancer therapy with a decreased risk of heating surrounding healthy tissues. We have also investigated the usefulness of this method using phantom experiments and reported that it is useful for controlling the temperature rise in magnetic hyperthermia [16] . Although this approach appears to be useful for focusing the heat deposition into the targeted tissue or organ, it would be necessary to investigate the effectiveness of this approach under various conditions of MNPs, AMF, and SMF. Furthermore, it would be desired to derive an equation describing the energy dissipation of MNPs in the presence of both the AMF and SMF for estimating and controlling the heat deposition into the targeted tissue or organ and for designing an effective local heating system.
Our purpose in this study was to present a method for estimating the SLP in magnetic hyperthermia in the presence of an external SMF and to investigate the SLP values estimated by this method under various conditions of MNPs, AMF, and SMF.
2. Materials and Methods
2.1. Theory
The magnetization relaxation equation of Shliomis [12] [14] is given by
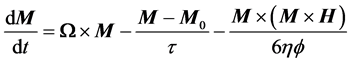 , (1)
, (1)
where M is the magnetization of MNPs under the magnetic field H, Ω is the flow velocity, f is the volume fraction, and η is the viscosity of the suspending fluid. When there is no bulk flow and M and H are collinear, Equation (1) is reduced to the following equation [6] :
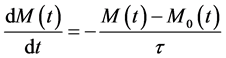 . (2)
. (2)
In Equation (2), τ is the effective relaxation time given by
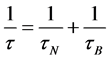 , (3)
, (3)
where τN and τB are the Néel relaxation and Brownian relaxation time, respectively [6] . τN and τB are given by the following relationships [6] :
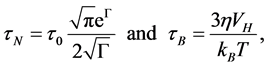 (4)
(4)
where τ0 is the average relaxation time in response to a thermal fluctuation, kB is the Boltzmann constant, T is the temperature, and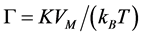 , with K being the anisotropy constant of MNP. VH is taken as the hydrodynamic volume of MNP that is larger than the magnetic volume
, with K being the anisotropy constant of MNP. VH is taken as the hydrodynamic volume of MNP that is larger than the magnetic volume 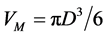 for MNP of diameter D. As a model for VH, it is assumed that
for MNP of diameter D. As a model for VH, it is assumed that , where δ is the thickness of a sorbed surfactant layer [6] .
, where δ is the thickness of a sorbed surfactant layer [6] . 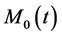 in Equation (2) denotes the equilibrium magnetization and is given by
in Equation (2) denotes the equilibrium magnetization and is given by
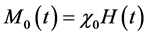 , (5)
, (5)
where χ0 and 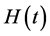 are the equilibrium susceptibility and magnetic field strength at time t, respectively. In this study,
are the equilibrium susceptibility and magnetic field strength at time t, respectively. In this study, 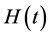 was assumed to be
was assumed to be
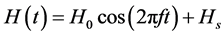 , (6)
, (6)
where H0 and f denote the amplitude and frequency of AMF, respectively, and Hs denotes the strength of an external SMF. Because the actual equilibrium susceptibility (χ0) is dependent on the magnetic field, χ0 was assumed to be the chord susceptibility corresponding to the Langevin equation, given by [6]
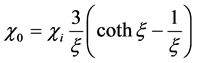 , (7)
, (7)
where χi is the initial susceptibility given by , ξ is the Langevin parameter given by
, ξ is the Langevin parameter given by , Md is the domain magnetization of a suspended particle, and μ0 is the permeability of free space. It should be noted that ξ is magnetic field (H) dependent and thus time dependent.
, Md is the domain magnetization of a suspended particle, and μ0 is the permeability of free space. It should be noted that ξ is magnetic field (H) dependent and thus time dependent.
Solving Equation (2) and using Equation (5) and Equation (6) yield
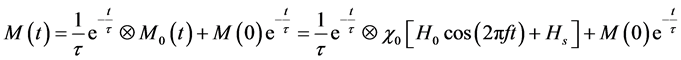 , (8)
, (8)
where 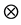 denotes the convolution integral and
denotes the convolution integral and 





The average rate of energy dissipation per cycle of the period, i.e., 


Substituting Equation (6) into Equation (9) yields

The rate of energy dissipation per unit mass of MNPs, i.e., SLP can be obtained from 

where ρ is the density of suspending fluid.
In this study, we considered a method for estimating the SLP, in which Equation (8) was used for 


It should be noted that when i is sufficiently large, the second term of the right-hand side of Equation (12) can be neglected and SLPi approaches the steady state. We denote the SLPi value in the quasi steady state by SLPqss. Actually, SLPqss was taken as the SLPi value in the case when the relative error (RE) was less than 10−10. The RE was defined by

where 
2.2. Simulation Studies
In this study, we assumed that MNPs consisted of two kinds of iron oxide nanoparticles, i.e., maghemite (γ-Fe2O3) and magnetite (Fe3O4). We fixed τ0, δ, Md, K, η, ρ, f, and T to be 10−9 s, 2 nm, 414 kA/m, 4.7 kJ/m3, 0.00235 kg/m/s, 4600 kg/m3, 0.003, and 37˚C, respectively, for maghemite [18] [19] . For magnetite, we fixed τ0, δ, Md, K, η, ρ, f, and T to be 10−9 s, 2 nm, 446 kA/m, 9.0 kJ/m3, 0.00235 kg/m/s, 5180 kg/m3, 0.003, and 37˚C, respectively [19] . When H0, f, and D were fixed, they were taken as 20 mT, 300 kHz, and 20 nm, respectively. It should be noted that the unit of mT can be converted to kA/m by use of the relationship 1 mT = 0.796 kA/m.
When considering the control of the temperature rise using the SMF with a gradient strength of Gs, the strength of the SMF at a distance of x from the FFP (Hs(x)) was given by

3. Results
As shown in Equation (12), the SLPi value depends on the cycle number of the M-H curve. Thus, we calculated the SLPi value in the quasi steady state, i.e., the SLPqss value under the condition in which the RE given by Equation (13) was less than 10−10, as previously described. Figure 1(a) shows the common logarithm of the RE given by Equation (13) as a function of the number of cycles for maghemite, whereas Figure 1(b) shows the case for magnetite. In these simulations, we neglected the second term in the right-hand side of Equation (12), because it approaches zero in the steady state. The τ value given by Equation (3) was 4.10 × 10−8 s and 1.71 × 10−6 s for maghemite and magnetite, respectively. As shown in Figure 1, the speed with which the SLPi value reached the quasi steady state depended on the τ value, i.e., the larger the τ value, the more slowly the SLPi value reached the quasi steady state. As shown in Figure 1(b), there was a tendency for the RE to increase with increasing Hs. Note that the plateau regions in Figure 1 correspond to the so-called “machine epsilon”.
Figure 2(a) shows the M-H curves in the quasi steady state calculated from Equation (8) at an f of 300 kHz for maghemite. In this case, Hs was varied from 0 to 30 mT with steps of 10 mT. For comparison, Figure 2(b) shows those for magnetite. It should be noted that 

Figure 4(a) shows the SLPqss values calculated from Equation (12) as a function of Hs with D being varied from 10 nm to 30 nm with steps of 5 nm for maghemite, whereas Figure 4(b) shows the case for magnetite. In these simulations, H0 and f were fixed at 20 mT and 300 kHz, respectively. As shown in Figure 4, the SLPqss value decreased with increasing Hs in all cases.

Figure 1. (a) Common logarithm of the relative error (RE) given by Equation (13) at various values of the static magnetic field (SMF) strength (Hs) (0, 25, and 50 mT) for magnetic nanoparticles (MNPs) consisting of maghemite; (b) Common logarithm of the RE given by Equation (13) at various Hs values (0, 25, and 50 mT) for MNPs consisting of magnetite. In these simulations, the amplitude (H0) and frequency (f) of an alternating magnetic field (AMF) and the diameter of MNPs (D) were assumed to be 20 mT, 300 kHz, and 20 nm, respectively. Note that the unit of mT can be converted to kA/m by use of the relationship 1 mT = 0.796 kA/m. The magnetic and physical properties of maghemite and magnetite used in this study are described in the “Simulation Studies” section. The specific loss power in the quasi steady state (SLPqss) was taken as the SLPi value calculated from Equation (12) in the case when the RE was less than the threshold (10−10 in this study).

Figure 2. (a) M-H curves (hysteresis loops) in the quasi steady state calculated from Equation (8) at various Hs values (0, 10, 20, and 30 mT) for maghemite; (b) M-H curves calculated from Equation (8) at various Hs values (0, 10, 20, and 30 mT) for magnetite. In these simulations, H0, f, and D were assumed to be 20 mT, 300 kHz, and 20 nm, respectively.

Figure 3. (a) M-H curves in the quasi steady state calculated from Equation (8) at various Hs values (0, 10, 20, and 30 mT) for maghemite; (b) M-H curves calculated from Equation (8) at various Hs values (0, 10, 20, and 30 mT) for magnetite. In these simulations, H0, f, and D were assumed to be 20 mT, 600 kHz, and 20 nm, respectively.

Figure 4. (a) Specific loss power in the quasi steady state (SLPqss) values calculated from Equation (12) as a function of Hs at various D values (10, 15, 20, 25, and 30 nm) for maghemite; (b) SLPqss values calculated from Equation (12) as a function of Hs at various D values (10, 15, 20, 25, and 30 nm) for magnetite. In these simulations, H0 and f were assumed to be 20 mT and 300 kHz, respectively. Note that the SLPqss values for D of 10 nm are too small to be seen in the figure.
Figure 5(a) shows the SLPqss values calculated from Equation (12) as a function of Hs with H0 being varied from 5 mT to 25 mT with steps of 5 mT for maghemite, whereas Figure 5(b) shows the case for magnetite. In these cases, D and f were fixed at 20 nm and 300 kHz, respectively. As in Figure 4, the SLPqss value decreased with increasing Hs in all cases.
Figure 6(a) shows the SLPqss values calculated from Equation (12) as a function of Hs with f being varied from 200 kHz to 1000 kHz with steps of 200 kHz for maghemite, whereas Figure 6(b) shows the case for magnetite. In these simulations, D and H0 were

Figure 5. (a) SLPqss values calculated from Equation (12) as a function of Hs at various H0 values (5, 10, 15, 20, and 25 mT) for maghemite; (b) SLPqss values calculated from Equation (12) as a function of Hs at various H0 values (5, 10, 15, 20, and 25 mT) for magnetite. In these simulations, f and D were assumed to be 300 kHz and 20 nm, respectively.

Figure 6. (a) SLPqss values calculated from Equation (12) as a function of Hs at various f values (200, 400, 600, 800, and 1000 kHz) for maghemite; (b) SLPqss values calculated from Equation (12) as a function of Hs at various f values (200, 400, 600, 800, and 1000 kHz) for magnetite. In these simulations,H0 and D were assumed to be 20 mT and 20 nm, respectively.
fixed at 20 nm and 20 mT, respectively. As in Figure 4 and Figure 5, the SLPqss value decreased with increasing Hs in all cases.
Figure 7(a) shows the SLPqss values calculated from Equation (12) as a function of the distance from the FFP (x) at various values of Gs (1, 2, 5, and 10 T/m) for maghemite, whereas Figure 7(b) shows the case for magnetite. In these simulations, Hs at x, i.e., Hs(x) was calculated from Gs and x using Equation (14), and D, H0, and f were fixed at 20 nm, 20 mT, and 300 kHz, respectively. As shown in Figure 7, the plot of the SLPqss values against x became narrow as Gs increased in both cases.

Figure 7. (a) SLPqss values as a function of the distance from a field-free point (x) at various gradient strength values of the SMF (Gs) (1, 2, 5, and 10 T/m) for maghemite; (b) SLPqss values as a function of x at various Gs values (1, 2, 5, and 10 T/m) for magnetite. In these simulations, D, H0, and f were assumed to be 20 nm, 20 mT, and 300 kHz, respectively.
4. Discussion
In this study, we presented a method for estimating the SLP in magnetic hyperthermia in the presence of both the AMF and SMF, which was derived by solving the magnetization relaxation equation of Shliomis [14] numerically. We also presented the results obtained by simulation studies under various conditions of MNPs, AMF, and SMF. Our results shown in Figure 4 to Figure 7 suggest that the SLP in magnetic hyperthermia can be controlled using the SMF and that our method will be useful for selecting the optimal parameters for controlling the temperature rise in magnetic hyperthermia in order to reduce the risk of overheating surrounding healthy tissues.
As shown in Figure 1, the RE given by Equation (13) for maghemite (Figure 1(a)) became less than the threshold (10−10 in this study) faster than that for magnetite (Figure 1(b)). As previously described, there was a large difference in the τ value given by Equation (3) between maghemite and magnetite (4.10 × 10−8 s and 1.71 × 10−6 s for maghemite and magnetite, respectively, under the condition described in the “Simulation Studies” section). Thus, the above difference appears to be due to a difference in the τ value. Similarly, a large difference in the M-H curve was observed between maghemite (Figure 2(a)) and magnetite (Figure 2(b)). This difference also appears to be due to a difference in the τ value.
As shown in Figure 2 and Figure 3, the area of the M-H curve calculated from Equation (8) decreased with increasing Hs. The area of the M-H curve directly represents the power loss during one cycle of the hysteresis loop. Thus, the above finding corresponds to the fact that SLPqss decreases with increasing Hs (Figure 4 to Figure 6).
We previously made an experimental device that allows for magnetic hyperthermia in the presence of the SMF that was generated using a Maxwell coil pair [16] . This device can also generate an FFP and move it by varying the DC electric currents applied to the individual Maxwell coils [16] . We investigated the effect of SMF on the temperature rise in magnetic hyperthermia using this device and then evaluated the feasibility of controlling the temperature rise using an SMF with an FFP under various conditions of the AMF and SMF. Our experimental results demonstrated that the SLP value (referred to as “SAR” in our previous paper [16] ) decreased with increasing Hs [16] . Thus, the present results shown in Figure 4 to Figure 6 appear to support our experimental results [16] . Furthermore, our experimental results showed that the area of local heating became narrow with increasing Gs. Conversely, it became broad with decreasing Gs [16] . As shown in Figure 7, the plot of the SLP values against the position from the FFP became narrow as Gs increased, whereas it became broad as Gs decreased. These results also appear to support our experimental results described above [16] .
In our previous study [16] , we treated the case in which the FFP is moved in one dimension by use of a single Maxwell coil pair. However, it would be possible to extend it to two or three dimensions by use of multiple Maxwell coil pairs. Theoretically, the magnetic field strength generated by a Maxwell coil pair can be calculated from the Biot-Savart law [20] . Thus, when the electric currents applied to the coils are known, the position of the FFP can be determined by solving the equations describing the magnetic field strength based on the Biot-Savart law [20] . Conversely, when the position of the FFP is given, the electric currents applied to the coils can be determined by the similar procedure. If this could be realized, it would become easy to control the position of the FFP, i.e., the position of local heating. As previously described, the plot of the SLP values against the position from the FFP became broad with decreasing Gs, whereas it became narrow with increasing Gs (Figure 7). These results suggest that the area of local heating can be controlled by varying the value of Gs. The Gs value can also be calculated from the Biot-Savart law [20] . Thus, it would become possible to control not only the position but also the area of local heating by controlling the electric currents applied to the coils based on the Biot-Savart law [20] . This will further enhance the feasibility and effectiveness of the magnetic hyperthermia with the temperature rise being controlled for reducing the risk of overheating surrounding healthy tissues.
In this study, we derived Equation (12) by solving the magnetization relaxation equation of Shliomis [14] (Equation (1)) with an assumption that there is no bulk flow and the magnetization of MNPs and magnetic field are collinear. In this case, Equation (1) is reduced to Equation (2), which can be easily solved using convolution integral as shown in Equation (8). Although Equation (2) appears to be valid in considering the magnetic hyperthermia with small MNPs in the superparamagnetic state and we believe that this study will provide the basis for establishing the effectiveness of such magnetic hyperthermia, it will be necessary to solve Equation (1) without any assumptions or another magnetization equation derived microscopically from the Fokker-Planck equation [12] for more detailed analysis. These studies are currently in progress. As previously described, we targeted the MNPs consisting of maghemite and magnetite with the magnetic and physical properties described in the “Simulation Studies” section. We will also perform further studies for the MNPs with other magnetic and physical properties and/or other MNPs.
Recently, Dhavalikar et al. [21] have theoretically investigated the feasibility of spatially-focused heating of MNPs guided by the SMF with a field-free region such as the FFP. In their study, the phenomenological magnetization equation derived by Martsenyuk et al. [22] was used instead of the Shliomis’ equation [14] . A comparative study of the present results and those based on the equation of Martsenyuk et al. [22] is also currently in progress.
5. Conclusion
We presented a method for estimating the SLP in magnetic hyperthermia in the presence of an external SMF, which is based on the numerical solution of the magnetization relaxation equation of Shliomis. We also presented the SLP values estimated under various conditions of MNPs, AMF, and SMF. Our method will be useful for estimating the SLP in the presence of both the AMF and SMF and for designing an effective local heating system using the SMF for magnetic hyperthermia in order to reduce the risk of overheating surrounding healthy tissues.
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (Grant Number: 25282131 and 15K12508) from the Japan Society for the Promotion of Science (JSPS).
Cite this paper
Murase, K. (2016) A Simulation Study on the Specific Loss Power in Magnetic Hyperthermia in the Presence of a Static Magnetic Field. Open Journal of Applied Sciences, 6, 839-851. http://dx.doi.org/10.4236/ojapps.2016.612073
References
- 1. Abe, M., Hiraoka, M., Takahashi, M., Egawa, S., Matsuda, C., Onoyama, Y., Morita, K., Kakehi, M. and Sugahara, T. (1986) Multi-Institutional Studies on Hyperthermia Using an 8-MHz Radiofrequency Capacitive Heating Device (Thermotron RF-8) in Combination with Radiation for Cancer Therapy. Cancer, 58, 1589-1595.
https://doi.org/10.1002/1097-0142(19861015)58:8<1589::AID-CNCR2820580802>3.0.CO;2-B - 2. Seip, R. and Ebbini, E.S. (1995) Noninvasive Estimation of Tissue Temperature Response to Heating Fields Using Diagnostic Ultrasound. IEEE Transactions on Biomedical Engineering, 42, 828-839.
https://doi.org/10.1109/10.398644 - 3. Gilchrist, R.K., Medal, R., Shorey, W.D., Hanselman, R.C., Parrott, J.C. and Taylor, C.B. (1957) Selective Inductive Heating of Lymph Nodes. Annals of Surgery, 146, 596-606.
https://doi.org/10.1097/00000658-195710000-00007 - 4. Jordan, A., Scholz, R., Maier-Hauff, K., Johannsen, M., Wust, P., Nodobny, J., Schirra, H., Schmidt, H., Deger, S., Loening, S., Lanksch, W. and Felix, R. (2001) Presentation of a New Magnetic Field Therapy System for the Treatment of Human Solid Tumors with Magnetic Fluid Hyperthermia. Journal of Magnetism and Magnetic Materials, 225, 118-126.
https://doi.org/10.1016/S0304-8853(00)01239-7 - 5. Murase, K., Aoki, M., Banura, N., Nishimoto, K., Mimura, A., Kuboyabu, T. and Yabata, I. (2015) Usefulness of Magnetic Particle Imaging for Predicting the Therapeutic Effect of Magnetic Hyperthermia. Open Journal of Medical Imaging, 5, 85-99.
https://doi.org/10.4236/ojmi.2015.52013 - 6. Rosensweig, R.E. (2002) Heating Magnetic Fluid with Alternating Magnetic Field. Journal of Magnetism and Magnetic Materials, 252, 370-374.
https://doi.org/10.1016/S0304-8853(02)00706-0 - 7. Neuberger, T., Schopf, B., Hofmann, H., Hofmann, M. and von Rechenberga, B. (2005) Superparamagnetic Nanoparticles for Biomedical Applications: Possibilities and Limitations of a New Drug Delivery System. Journal of Magnetism and Magnetic Materials, 293, 483-496.
https://doi.org/10.1016/j.jmmm.2005.01.064 - 8. Ito, A., Shinkai, M., Honda, H. and Kobayashi, T. (2005) Medical Applications of Functionalized Magnetic Nanoparticles. Journal of Bioscience and Bioengineering, 100, 1-11.
https://doi.org/10.1263/jbb.100.1 - 9. Lee, J.H., Jang, J.T., Choi, J.S., Moon, S.H., Noh, S.H., Kim, J.W., Kim, I.S., Park, K.I. and Cheon, J. (2011) Exchange-Coupled Magnetic Nanoparticles for Efficient Heat Induction. Nature Nanotechnology, 6, 418-422.
https://doi.org/10.1038/nnano.2011.95 - 10. Kuboyabu, T., Yamawaki, M., Aoki, M., Ohki, A. and Murase, K. (2016) Quantitative Evaluation of Tumor Early Response to Magnetic Hyperthermia Combined with Vascular Disrupting Therapy Using Magnetic Particle Imaging. International Journal of Nanomedicine and Nanosurgery, 2, 1-7. http://dx.doi.org/10.16966/2470-3206.114
- 11. Ohki, A., Kuboyabu, T., Aoki, M., Yamawaki, M. and Murase, K. (2016) Quantitative Evaluation of Tumor Response to Combination of Magnetic Hyperthermia Treatment and Radiation Therapy Using Magnetic Particle Imaging. International Journal of Nanomedicine and Nanosurgery, 2, 1-6. http://dx.doi.org/10.16966/2470-3206.117
- 12. Soto-Aquino, D. and Rinaldi, C. (2010) Magnetoviscosity in Dilute Ferrofluids from Rotational Brownian Dynamics Simulations. Physical Review E, 82, Article ID: 046310.
https://doi.org/10.1103/PhysRevE.82.046310 - 13. Murase, K. (2016) Methods for Estimating Specific Loss Power in Magnetic Hyperthermia Revisited. Open Journal of Applied Sciences, 6, 815-825.
https://doi.org/10.4236/ojapps.2016.612071 - 14. Shliomis, M.I. (1972) Effective Viscosity of Magnetic Suspensions. Soviet Physics JETP, 34, 1291-1294.
- 15. Tasci, T.O., Vargel, I., Arat, A., Guzel, E., Korkusuz, P. and Atalar, E. (2009) Focused RF Hyperthermia Using Magnetic Fluids. Medical Physics, 36, 1906-1912.
https://doi.org/10.1118/1.3106343 - 16. Murase, K., Takata, H., Takeuchi, Y. and Saito, S. (2013) Control of the Temperature Rise in Magnetic Hyperthermia with Use of an External Static Magnetic Field. Physica Medica, 29, 624-630.
https://doi.org/10.1016/j.ejmp.2012.08.005 - 17. Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in C. Cambridge University Press, Oxford.
- 18. Murase, K., Oonoki, J., Takata, H., Song, R., Angraini, A., Ausanai, P. and Matsushita, T. (2011) Simulation and Experimental Studies on Magnetic Hyperthermia with Use of Superparamagnetic Iron Oxide Nanoparticles. Radiological Physics and Technology, 4, 194-202.
https://doi.org/10.1007/s12194-011-0123-4 - 19. Maenosono, S. and Saita, S. (2006) Theoretical Assessment of FePt Nanoparticles as Heating Elements for Magnetic Hyperthermia. IEEE Transactions on Magnetism, 42, 1638-1642.
https://doi.org/10.1109/TMAG.2006.872198 - 20. Jackson, J.D. (1999) Classical Electrodynamics. Wiley, New York.
- 21. Dhavalikar, R. and Rinaldi, C. (2016) Theoretical Predictions for Spatially-Focused Heating of Magnetic Nanoparticles Guided by Magnetic Particle Imaging Field Gradients. Journal of Magnetism and Magnetic Materials, 419, 267-273.
https://doi.org/10.1016/j.jmmm.2016.06.038 - 22. Martsenyuk, M.A., Raikher, Y.L. and Shliomis, M.I. (1974) On the Kinetics of Magnetization of Ferromagnetic Particle Suspension. Soviet Physics JETP, 38, 413-416.

